硫化物在铂电极上电氧化时空动力学的模型模拟和分析

杨加平 于辉耀 何瑜庥 解京选 毕文彦 高庆宇

(中国矿业大学化工学院,江苏徐州221116)

1 Introduction

The electrochemical oxidation of sulfide has been frequently studied1-4in experiment on platinum electrode.Due to its complicated oxidation process,the electro-oxidation of sulfide possesses complex spatiotemporal dynamic behaviors.Oscillations in this electrochemical system were firstly investigated by Helms and coworkers in 1998.5It was found that both current and potential oscillated spontaneously with time.Later in 2006,Miller and Chen6expanded the study of electro-oxidation of sulfide on platinum,and the results showed that current oscillations and two distinct potential oscillations occurred.These two potential oscillations were classified as hidden N-shaped negative differential resistance(HN-NDR)oscillators.7,8Feng et al.9further detected this system and found that both N-shaped negative differential resistance(N-NDR)and HN-NDR types of oscillations exhibited in this system.In N-NDR oscillatory region abundant temporal dynamics including simple oscillations,complex oscillations,and bistable behaviors existed in the sulfide electro-oxidation process on platinum.Deposition and dissolution of sulfur layer on the platinum electrode surface were the general processes in the oscillatory regions.Motivated by the rich temporal dynamic behavior,Zhao et al.10investigated the spatiotemporal patterns and found synchronization of sulfur deposition/dissolution,pulses,and twinkling-eye patterns in N-NDR oscillatory region.In other potential regions patterns including fronts and labyrinths were also observed.When perturbed with some adsorbing anions,this system exhibited different dynamic behaviors.HN-NDR oscillations were investigated when appropriate amount of chloride were added into this system and in the N-NDR region the pulses morphology was changed greatly.11

Abundant spatiotemporal patterns were obtained in the electrooxidation of sulfide in experiment.Nevertheless,mechanistic model and analysis for the sulfide electrochemical system have not been reported yet.In a series of works12-14mechanisms for homogeneous dynamics of sulfide electrochemical system have been discussed.The dominate sulfide species in solution was sulfide ion(S2-)at pH>13.15The experiments for spatiotemporal pattern formation in our previous works9-11were performed in 1.00 mol·L-1sodium sulfide whose pH value was 13.6.The detailed mechanism for the oscillatory region,especially for the N-NDR oscillations,was put forward to well understand the oscillations and pattern formation.The autocatalytic character of the double-layer potential as the positive feedback induced the formation of platinum hydroxide and platinum oxide(R1 and R2),respectively)on the electrode surface,which could catalyze the oxidation of the surface sulfide ion to generate elementary sulfur,(R3 and R4).The deposited sulfur further reacted with sulfide ion to produce soluble polysulfide(S22-)through R5 and as a result the unoccupied site of platinum was released again for electrocatalytic oxidation or direct electro-oxidation.Then the platinum hydroxide and platinum oxide could be reproduced,and the steps expressed above occurred repeatedly resulting in continuous oscillations and patterns.

where ads and surface,as the subscripts,denote species adsorbing and locating at the electrode surface,respectively.And Sn2-stands for soluble polysulfide(n is the integer and n>1).

It is known that N-NDR oscillations in electrochemistry mainly caused by the interaction of double-layer potential autocatalytic process and mass-transport limited negative feedback.16Consequently,the formation of platinic hydroxide and platinum oxide induced the NDR as the positive feedback.The mass-transport limited step of sulfide ion from the bulk solution to the interface of electrode/electrolyte for platinic hydroxide and platinum oxide reduction contributed a slow negative feedback to this system.Elemental sulfur(S)in R4 could strongly adsorb on the active sites of platinum and inhibit the growth of platinic hydroxide and platinum oxide.17Therefore,during the electrooxidation of sulfide on platinum electrode the negative feedbacks included the S2-limited mass-transport and elemental sulfur adsorption,which could both inhibit the formation of platinic hydroxide and platinum oxides.One positive feedback involved in electron-transfer process interacted with two negative feedbacks leads to complex dynamic behaviors.In this work we aim to simulate and explain the complex spatiotemporal dynamics with a simplified model according to reaction mechanism in electrochemical oxidation of sulfide.

2 Model

According to the detailed mechanism of sulfide electro-oxidation on platinum,we obtained a mechanistic model(M1-M3)as follows:

Here bulk as a subscript denotes species in the electrolyte.M1 expresses the mass-transport limited step of sulfide ion from the bulk solution to the interface of electrode/electrolyte.M2 denotes the S2-electro-oxidation and sulfur deposition,resulting from R1+R3 or R1+R2+R4.M3 describes the dissolution of the poison(i.e.,deposited sulfur)and the rebirth of active sites on platinum.The experiment was operated in a conventional three-electrode cell.Working electrode(WE)was a platinum disk embedded in a Teflon insulator with a diameter of 2.0 mm.The counter electrode(CE)was a platinum ring placed at 1.5 cm below the WE.A saturated calomel electrode(SCE)was used as the reference electrode(RE)and was connected to the bulk electrolyte through a salt bridge.The experiments were conducted by a CHI-660A electrochemical workstation(CH Instruments Inc.,USA).A charge-coupled device(CCD)camera was utilized to investigate the pattern formation on the WE.The schematic diagram of the three-electrode system is shown in Fig.1.The model and simulation were performed based on this system.

The spatiotemporal dynamics of double-layer potential can be derived according to the current balance of the circuit.Since electrolyte solution is electroneutral,the uncompensated resistance of the electrolyte is related to the distance between WE and RE.18Therefore the set of dynamic equation of double-layer potential19is given by

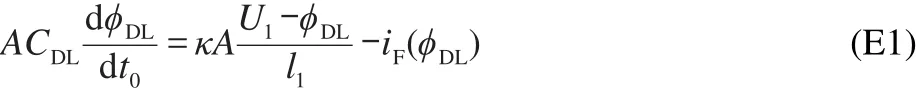
where U1is the applied potential;ϕDLdenotes the double-layer potential;CDLis the double-layer capacitance per unit area;l1describes the distance between WE and RE;A stands for the area of the WE;κ presents the conductivity of the electrolyte;and t0is the time.The left side of equation(E1)describes the double-layer capacitive charging current.The first term on right side of the equation denotes the migration current induced by the electric field and iF(ϕDL)presents the Faradaic current.Generally iF(ϕDL)can be formulated as20

where n is the number of electrons in the charge-transfer process;csdenotes the concentration of active substance S2-at electrode/electrolyte interface;and F is the Faradaic constant.k(φDL)is the rate constant.Therefore,as the electrochemical reaction occurs,the concentration of active substance at the interface will decrease.The replenishment of the substances includes diffusion from bulk electrolyte and migration process.Thus the net concentration evolution rate21at the electrode/electrolyte interface can be described as

Fig.1 Schematic diagram of the three-electrode system

where D is the diffusion constant;cbulkdenotes the bulk concentration of S2-;μdescribes the mobility of the S2-,andδpresents the diffusion layer thickness,which is assumed independent with time and space.The first term on the right side of equation(E3)indicates the diffusion of S2-from the bulk solution towards the electrode.The second term on the right side of the equation means that the S2-is driven by migration to the electrode,and the last term shows the reaction occurring at the electrode.As is mentioned that adsorbed poison can reduce the real active area of the electrode,here the poison is adsorbed elemental sulfur inhibiting the electrochemical oxidation of sulfide.Thus the coverage of elemental sulfur on the electrode surface,θ,is introduced to modify the effective area.The time evolution rate of θ involves two main processes.One is the potential-dependent adsorption process and the other is potentialindependent desorption process.As a consequence,the set of time evolution rate of θ is given by

where kais the adsorption rate constant;Padenotes the fugacity of the adsorbate,and kdpresents the desorption rate constant.The electrochemical oxidation of sulfide can only occur at the site that is not blocked by the poison.Therefore the Faradaic current and the net concentration evolution rate are modified as

The three-variable model comprising equations(E1)and(E4)-(E6)is the homogeneous model which can be used to simulate the sulfide electro-oxidation system.For the homogeneous calculation we employ Euler method to solve the dynamic equations.In order to simplify the calculation and make the model more general,we used a dimensionless form by converting the time,double-layer potential,applied potential,concentration of active substance,and the distance between WE and RE into dimensionless quantities using the following terms:

3 Results and discussion

3.1 Homogeneous dynamic behavior

Fig.2 Simulated current response for a potential sweep

Fig.2 shows the simulated current response for a potential sweep.Current oscillations are seen in the NDR region along the N-shaped curve.In this region,the NDR is caused by the early formation of platinic hydroxide and platinum oxides.The current density undergoes an increasing process as a result the concentration of S2-at the electrode/electrolyte interface is reduced abruptly.The diffusion of S2-from the bulk to the interface is thus the limited step in this system.Therefore,one negative feedback is caused by the S2-diffusion limited step.Meanwhile,PtSadscan also affect the dynamic behaviors of this system.Adsorbed S as a poison in the fuel cell adsorbs strongly on the active site of the metal electrode.22,23The strong adsorption of elemental S can inhibit the formation of platinic hydroxide and platinum oxides and consequently introduces another negative feedback into the system.With one electron-transfer involved positive feedback and two negative feedbacks,the three-variable model is simulated to possess an N-NDR oscillatory behavior in the negative slop branch of the dynamic curve(Fig.2).

In the N-NDR oscillatory region,simulated time-series of current densities are investigated under potentiostatic control.It is shown in Fig.3 that oscillation mode varies with applied potential.In the oscillatory region,it starts with simple oscillations,shown in Fig.3a.Then when potential is kept at 7.25 the current density oscillates in a complex way,namely 11oscillation modes,c.f.,Fig.3b.Further increasing the applied potential results in more complex spontaneous current oscillations,including 12and complex ones(Fig.3c and Fig.3d).As the potential is increased to 7.56,the current oscillates again in a simple mode,seen in Fig.3e.At U=7.60,oscillations are not stable anymore.

3.2 Spatiotemporal dynamics

In electrochemical system,the diffusion and migration of electroactive species strongly influence the inherent spatiotemporal dynamic behavior.With the disk platinum electrode,diffusion and migration occur not only in the vertical direction of the electrode but also in the parallel direction due to concentration and potential differences at different local sites.Therefore the transport in both parallel and vertical directions against the electrode surface can affect the spatiotemporal dynamics of the electrochemical system.Thus the model above should be modified to calculate the spatiotemporal patterns forming in the electrode surface.Diffusion and migration of moving species on electrode surface are considered in mass balance equation.In spatiotemporal dynamical system,the ordinary differential equations are changed into partial differential ones on account of the dynamic interaction of different sites on the electrode surface.The diffusion and migration in the parallel direction are considered and described as the second order partial derivatives in space.Here,it is assumed that the electrolyte resistance between WE and RE is proportional to the distance of WE and RE.Linear gradient in electric field perpendicular to the WE surface is approximated,and then calculation of Laplace equation for distribution of electric field in bulk electrolyte is eliminated.The same dimensionless terms are introduced into the differential equations as a result the dimensionless equations of surface variables(ϕ,c,and θ)are written as:

Other parameters have the same meaning and expression as the homogeneous model.The last two terms in the concentration evolution equation describe the parallel diffusion and migration transportation,respectively.Therefore,the homogeneous dynamics interaction with spatial couplings results in complex spatiotemporal patterns.Here we adopt the five-point difference method to simulate the spatiotemporal patterns.

Fig.4 illustrates twinkling-eye waves and time series of current densities during the numerical simulation.This result is performed on a 0.2×0.2 space lattice.It is observed in Fig.4b that the total current density oscillates chaotically with time due to the spatial coupling,which results in the spatial heterogeneity.However,the oscillations of current density in homogeneous condition are simple oscillations.As a result the transportation of electroactive species in the parallel direction has a great effect on the dynamics of the system.The spatial coupling of different local sites induces non-uniform distribution of current on the whole electrode surface.General dynamics interaction with spatial couplings induced by the concentration gradient and electric field in both parallel and vertical directions results in complex spatiotemporal dynamics.Thus the patterns formed under this condition are non-uniform twinklingeye waves as shown in Fig.4a(movie in Supporting Information).

Fig.3 Simulated time-series of current densities under potentiostatic control

Fig.4 Twinkling-eye waves(a)and time-series of current densities(b)in the numerical simulation

Fig.5 Snapshots of traveling waves in simulation(a,b)and in experiment(c,d)

In the sulfide electro-oxidation experiment traveling waves of sulfur are generally observed,shown in Fig.5(c,d).The waves are randomly triggered at the sites of the electrode and propagate on the surface.Generally,if the excitation site is not at the edge of the electrode,the traveling waves commonly propagate as the spiral and target waves.One wave will annihilate either with the other wave or with the edge of the electrode.This phenomenon is reproduced by the model simulation with appropriate parameters.Fig.5(a,b)shows the simulated traveling waves in a 0.2×0.2 space lattice.From the mechanism point of view,elemental sulfur adsorption on one hand can block the active sites of the electrode and thus inhibit the electrochemical reaction,and on the other hand can induce the non-uniform distribution of both concentration and potential through the whole electrode surface,which as a result introduces the spatial coupling to the system.It was known that the range and strength of spatial coupling in the electrochemical system are greatly related to the distance between WE and RE and the conductivity of electrolyte,respectively.24-26The range and strength of spatial coupling have great effects on the spatiotemporal patterns.With appropriate value of parameters,the positive and negative electrochemical feedbacks,interacting with spatial coupling,induce interesting traveling waves in the model simulation,shown in Fig.5(a,b).Spiral waves are stimulated at a defect site in space and propagate outspread the lattice.The tip of the spiral wave grows in an internal rotation way and the wave arm colliding with each other or with the space border also results in annihilation.Model simulation is consistent with experiment about pattern morphology and wave evolution.

In homogeneous system,it has been observed that the sulfide electro-oxidation system can spontaneously generate complex oscillations with appropriate parameters.It is suggested that complicated patterns may exist in this system.Therefore,we perform the simulation with spatiotemporal dynamical model to investigate the complex patterns.The result shows that two-arm spiral waves of double-layer potential are present with some certain parameters in a 0.8×0.8 space lattice,seen in Fig.6(a-d).Two singular points are generated in space and move around each other as a result two spiral waves are triggered.It also can be seen that the two tips of spiral waves move alternately close and apart and collide together at some specific time as shown in Fig.6b(movie in Supporting Information).The spatiotemporal evolution at the black line in Fig.6a is analyzed and it can be clearly observed in Fig.6e that the two tips of spiral waves move close and apart.

Fig.6 Two-armed spiral waves and space-time diagram

4 Conclusions

The spatiotemporal dynamics during the electro-oxidation of sulfide on platinum is further understood in the work.In this paper we presented a detailed model for the homogeneous and transportation-coupled spatiotemporal dynamics of sulfide electro-oxidation.It was found that simple and complex current oscillations exist in homogeneous system.Poison(adsorbed elemental sulfur)that blocks the active sites of electrode and inhibits the formation of platinic hydroxide and platinum oxides plays an important role in the dynamics of this system.The coupling between one positive feedback,involved in an electron-transfer process,and two negative feedbacks,which consists of mass-transport limited step and poison-adsorption process,results in complex dynamic behaviors.

We took the spatial coupling into account to investigate the spatiotemporal patterns.The spatially extended model was modified based on the homogeneous model.We considered the transportation of electroactive species on both parallel and vertical directions to the electrode.Thus the model agreed better with the real situation.The model simulations obtained complicated patterns including twinkling-eye patterns and traveling waves,which was compared to the experiment results and found to possess the same evolution principles.In some certain parameters more complex patterns were obtained,e.g.,two-arm spiral waves spontaneously formed and propagated in a steady way.This opens an interesting perspective of explaining and predicting the pattern formation in electrochemical systems.Moreover,investigation and control of the complex patterns will have the potential value to promote the applications of functional devices.

Supporting Information: Movies for Fig.4 and Fig.6 are available free of charge via the internet at http://www.whxb.pku.edu.cn.

(1)O′Brien,J.A.;Hinkley,J.T.;Donne,S.W.Electrochim.Acta 2011,56,4224.doi:10.1016/j.electacta.2011.01.092

(2) Dutta,P.K.;Rabaey,K.;Yuan,Z.;Keller,J.Water Res.2008,42,4965.doi:10.1016/j.watres.2008.09.007

(3) Cai,J.;Zheng,P.Bioresource Technol.2013,128,760.doi:10.1016/j.biortech.2012.08.046

(4) Haner,J.;Bejan,D.;Bunce,N.J.J.Appl.Electrochem.2009,39,1733.doi:10.1007/s10800-009-9873-7

(5) Helms,H.;Schlömer,E.;Jansen,W.Monatsh.Chem.1998,129,617.

(6) Miller,B.;Chen,A.J.Electroanal.Chem.2006,588,314.doi:10.1016/j.jelechem.2006.01.006

(7) Strasser,P.;Eiswirth,M.;Koper,M.T.M.J.Electroanal.Chem.1999,478,50.doi:10.1016/S0022-0728(99)00412-X

(8) Kiss,I.Z.;Sitta,E.;Varela,H.J.Phys.Chem.C 2012,116,9561.

(9) Feng,J.;Gao,Q.;Xu,L.;Wang,J.Electrochem.Commun.2005,7,1471.doi:10.1016/j.elecom.2005.10.004

(10)Zhao,Y.;Wang,S.;Varela,H.;Gao,Q.;Hu,X.;Yang,J.;Epstein,I.R.J.Phys.Chem.C 2011,115,12965.doi:10.1021/jp202881h

(11) Yang,J.;Song,Y.;Varela,H.;Epstein,I.R.;Bi,W.;Yu,H.;Zhao,Y.;Gao,Q.Electrochim.Acta 2013,98,116.doi:10.1016/j.electacta.2013.03.042

(12) Waterston,K.;Bejan,D.;Bunce,N.J.Appl.Electrochem.2007,37,367.doi:10.1007/s10800-006-9267-z

(13)Parker,G.K.;Watling,K.M.;Hope,G.A.;Woods,R.Colloid.Surf.A:Physicochem.Eng.Aspects 2008,318,151.doi:10.1016/j.colsurfa.2007.12.029

(14) O′Brien,J.A.;Hinkley,J.T.;Donne,S.W.;Lindquist,S.E.Electrochim.Acta 2010,55,573.doi:10.1016/j.electacta.2009.09.067

(15) Hamilton,I.C.;Woods,R.J.Appl.Electrochem.1983,13,783.doi:10.1007/BF00615828

(16) Krischer,K.In Advance in Electrochemical Science and Engineering;Wielry-VCH:Weinheim,2003;Vol.8,pp 90-203.

(17)Kapusta,S.;Viehbeck,A.;Wilhelm,S.M.;Hackerman,N.J.Electroanal.Chem.Interfacial Electrochem.1983,153,157.doi:10.1016/S0022-0728(83)80011-4

(18) Krischer,K.;Varela,H.;Bı̂rzu,A.;Plenge,F.;Bonnefont,A.Electrochim.Acta 2003,49,103.doi:10.1016/j.electacta.2003.04.006

(19) Mazouz,N.;Krischer,K.J.Phys.Chem.B 2000,104,6081.doi:10.1021/jp000203+

(20) Koper,M.T.M.Electrochim.Acta 1992,37,1771.doi:10.1016/0013-4686(92)85080-5

(21) Flätgen,G.;Krischer,K.J.Chem.Phys.1995,103,5428.doi:10.1063/1.470578

(22) Galea,N.M.;Kadantsev,E.S.;Ziegler,T.J.Phys.Chem.C 2007,111,14457.doi:10.1021/jp072450k

(23) Fu,Y.;Zu,C.;Manthiram,A.J.Am.Chem.Soc.2013,135(48),18044-7.doi:10.1021/ja409705u

(24) Flätgen,G.;Krischer,K.Phys.Rev.E 1995,51,3397.doi:10.1103/PhysRevB.51.3397

(25) Mazouz,N.;Flätgen,G.;Krischer,K.Phys.Rev.E 1997,55,2260.doi:10.1103/PhysRevE.55.2260

(26) Plenge,F.;Li,Y.J.;Krischer,K.J.Phys.Chem.B 2004,108,14255.doi:10.1021/jp037955z