基于过完备结构字典的跳频信号稀疏分解

李斌武，李永贵，张敬义

(1．解放军理工大学通信工程学院，江苏南京210007;2．南京电讯技术研究所，江苏 南京210007)

0 引言

跳频信号作为一种典型的非平稳信号［1－2］，是现实生活中常用的信号之一。但是随着跳频带宽越来越宽，传统的采样和数据处理方法难以满足跳频信号带宽和数据处理量日益增大的需求，同时也忽视了现有硬件采样设备的采样速率限制。压缩感知(CS，Compressed Sensing)理论作为近些年在信号处理领域研究的热点理论，为跳频信号的采样和处理提供了一个新的思路。该理论前提条件就是要求信号具有稀疏性或可压缩性。然而现实中许多信号本身不具有稀疏性，而是在特定的变换域才会表现出稀疏特性。信号稀疏表示(Sparse Representation)是研究信号稀疏特性的重要理论，它可以有效提取信号最本质的特征，有利于信号的后续处理，可从本质上降低信号处理成本。因此，在数字信号处理应用中，人们总是用信号在某个域上的稀疏逼近取代原始数据表示，称为信号表示。信号表示多为加性分解，如傅里叶变换和小波变换分别将信号在三角函数和小波基上展开，在频域和小波域表示信号［3］;时频分析将信号在时频面展开，在时频域表示信号［4］。信号的稀疏表示就是用尽量少的基函数在某个变换域将信号展开，旨在从本质上描述信号。但是传统的信号稀疏表示是建立在正交基上的信号分解，该方法具有一定的局限性，往往不能够达对频率随时间不断变化的信号进行最佳的稀疏表示。

过完备字典(Over－complete Dictionary)下的信号稀疏分解能够得到更好稀疏表示效果。信号在过完备字典上分解的思想首先由Mallat和Zhang于1993年提出［5］。通过在过完备字典上的分解，用来表示信号的基可以自适应地根据信号本身的特点灵活选取。从而分解得到信号的一个非常简洁的表达，即稀疏表示，得到信号稀疏表示的过程则被称为信号的稀疏分解(Sparse Decomposition)。过完备字典下的信号分解具有更强的稀疏表达能力。由于信号稀疏表示的优良特性，它已经被应用到信号处理的许多方面，如信号去噪、信号编码和识别等［6］。其中，在信号时频分布研究方面的应用特别值得关注。

过完备字典下的信号稀疏分解能够充分利用跳频信号的本质及结构特征，可以有效揭示非平稳信号的时频结构，从而得到跳频信号的更优稀疏表示。因此，文中在分析跳频信号稀疏特性的基础上，构造基于跳频信号结构特性的过完备字典，并采用FFT改进的匹配追踪算法研究跳频信号的稀疏分解，提出了基于过完备结构字典的跳频信号稀疏表分解方法。仿真结果表明文中方法在跳频信号分解效果和算法用时方面都具有明显的优势。

1 跳频信号模型及其过完备结构字典

1．1 跳频信号模型

跳频信号是一种频率随时间随机变化的非平稳信号，其载波频率的变化受伪随机序列控制。跳频信号的每一跳都可以看成是在时域互相不重叠的有限长正弦信号［7］，所以某段时间内的跳频接收信号在可以看成是一系列加窗正弦信号的线性叠加。因此，可以将跳频信号表示如下:

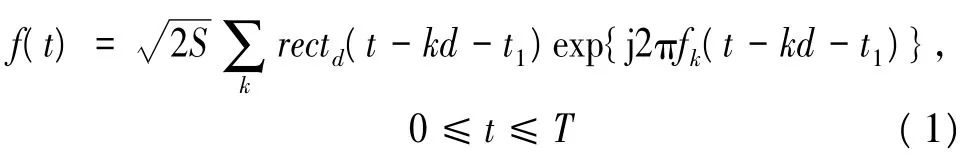
式中，S为信号功率，T为观测时间，rectd(t)是宽度为d的矩形窗:

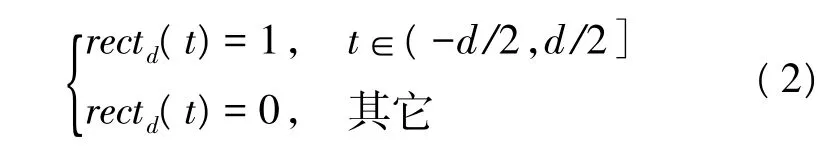
式中，d为跳周期，fk为第k跳的中心频率。

1．2 过完备结构字典

对于跳频信号的稀疏性，文献［6］中提出了局部傅里叶稀疏信号的概念。概念指出，如果一个信号在时间域中的每个点都能够用恒定频率的少量正弦信号来很好的近似表示，则称这个信号具有局部傅里叶稀疏特性。很明显，跳频信号是一种典型的局部傅里叶稀疏信号。当用像短时傅里叶变换

式中，fk表示第k个正弦函数对应的频率，其取值为频段内所有跳频频点数Nf;Tk为对应的第k跳信号的时间中心，且 Tk∈［0，d/2］，d为跳频信号跳周期，即正弦窗宽度。按照实际中需要的精度来均匀取值，如 k=1，2，…，Nn，Nn的精度由采样间隔决定，而Nn的取值决定了搜索精度，值越大搜索精度越高。对参数向量 γ 进行离散化 γ={Δu，iΔT，d，jΔf}，为减少字典生成所需时间，这里将d固定为一个很小的值，其他参数如下:Δu=1/2，2πΔf=π/2，2πΔfΔT=π/6，所以 Δu=1/2，Δf=1/4，ΔT=1/3，0≤j≤1，0≤i≤12。通过以上描述构造过完备的跳频信号结构字典 D={gγ(t)}γ∈Γ，则该字典中共有 M=NfNn个原子。(STFT)这样的时频表示方法进行表示时，跳频信号是稀疏的。也就是说跳频信号在时频表示的短时傅里叶变换下得到的系数是稀疏的，即跳频信号在局部傅里叶变换基下是稀疏的。很明显这里的局部傅里叶变换基是一个完备的正交基，对于频率随时间变化的跳频信号，稀疏表示效果欠佳。如果从跳频信号结构出发构造过完备字典，则会得到更好的稀疏表示效果。

根据式(1)所描述的跳频信号模型，多个具有不同时频中心的单音频信号相互叠加即可构成一段跳频信号，所以它的每一跳都可以看成是由时间中心Tk、载波频率fk和跳周期d三个参数唯一确定的时域不重叠的有限长正弦信号。而作为合作方通信，跳周期一般是已知的，为了能更好的分解跳频信号，根据跳频信号的结构特点选取由参数向量γ={Tk，dk，fk}确定的加窗正弦函数作为过完备字典的原子，这些加窗正弦函数具有单位能量，原子表达式如下所示:

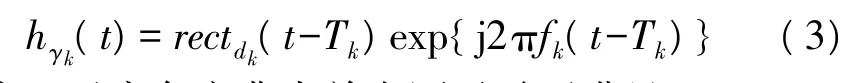
由于过完备字典中单个原子需要满足‖g‖=1，即范数为1。因此，对上式进行归一化得到原子为:

2 基于FFT－MP算法的信号稀疏分解

假设待分解信号是一个长度为N的信号f。若要在一组完备的正交基上分解该信号，则该正交基的数目应该是N。由于这些基之间相互正交，所以它们信号空间中的分布是稀疏的，因此信号分解后的信号能量将在不同的正交基上分散分布。但是，这样的分解通常导致信号表示不是稀疏的。而将信号在过完备字典上进行分解一定能够获得稀疏的分解结果［5］。

匹配追踪(MP)算法［5］是目前信号稀疏分解最常用的方法，其分解信号的具体过程阐述如下:

首先从生成的过完备字典中选出与待分解信号最匹配的原子gγ0，该原子满足如下条件:

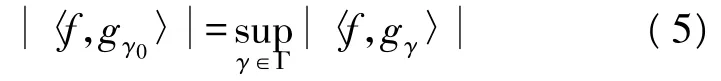
此时，信号被分解为两部分，即在最佳原子gγ0上的分量和信号残差:

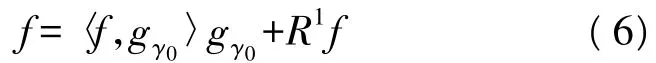
式中，R1f是信号f经过第一次最佳匹配之后的信号残差。显然原子gγ0和残差R1f是正交的，因此可得:

分解的最终目标是让残余信号的能量最小化。对每一次最佳匹配后的残差信号不断进行上述同样的分解过程，假设已经进行了k次原子分解，得到第k次分解后残差Rkf，则该残差可以被分解为:

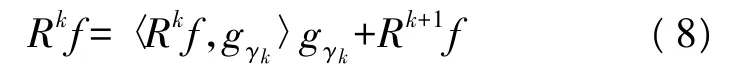
式中 gγk满足:

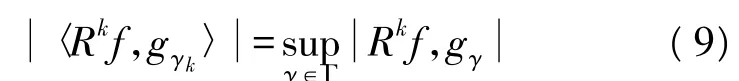
同样 Rk+1f与 gγk正交，满足:

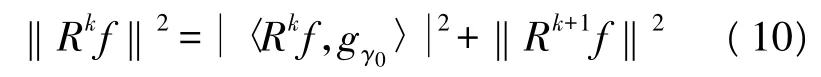
通过以上过程对信号进行n次分解，最终得到:

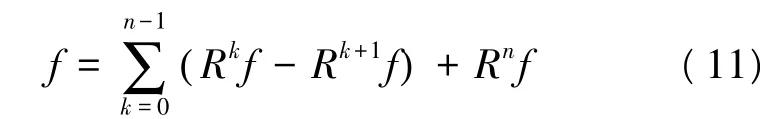
将式(8)带入上式可得:

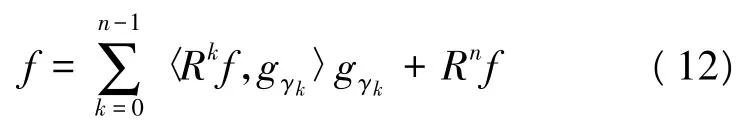
相似地，可以将‖f‖2分解为如下的连加等式:

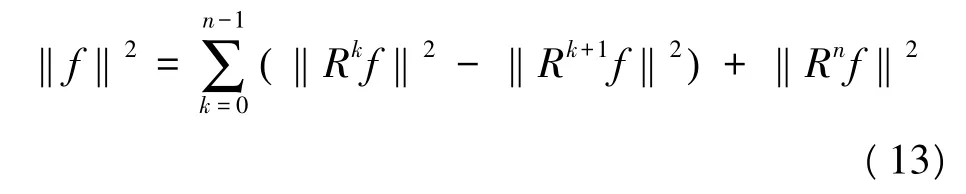
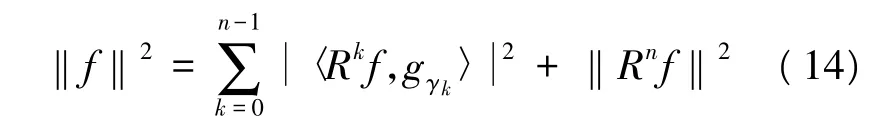
式中，Rnf为原信号用n个原子的线性组合表示之后产生的误差。已经证明在有限的信号长度下，残余信号能量‖Rnf‖随着n的增大呈指数衰减，最终为0。因此，信号可以被分解为:

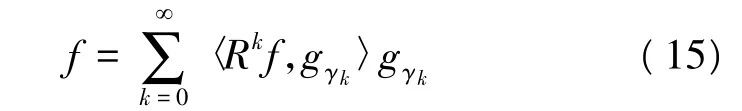
将式(10)带入上式得到一个能量守恒方程:

一般来说，由于‖Rnf‖的衰减特性，因此信号的信号的主要成分通常用很少的原子即可表示:

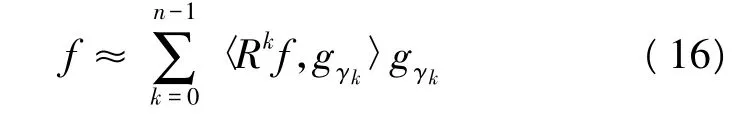
这里n是远小于信号长度N的。

目前MP算法还是一种比较常用的信号稀疏分解方法，但是在利用MP算法进行信号稀疏分解的过程中，每次分解都要计算信号残差在过完备字典中所有原子上的投影，并且是在高维空间进行，因此计算量巨大。通常基于MP算法的稀疏分解需要在N维空间进行多次的内积计算〈Rkf，gγ〉，这使得信号稀疏分解过程的计算量巨大。文献［8］针对基于MP算法在稀疏分解中多次进行计算高维空间内积计算量偏大的问题，提出了一种基于FFT改进的MP信号稀疏分解方法。

对于过完备字典中一个由参数 γ=(s，u，v，w)唯一确定的原子，当信号长度为N时，如果让u在［0，N－1］上取所有可能的值，则该原子要和信号或信号的残差作N次内积运算〈Rkf，gγ〉。虽然这样对信号的稀疏分解效果会更好，但这会使字典的规模增加，从而造成计算量的大幅增加。但是由于u从0到N－1连续取值，因此可以将所有的N次内积计算转换成一次Rkf和gγ的互相关运算，即r(Rkf，gγ)。

由于互相关运算可以利用离散傅里叶变换的快速算法FFT快速实现，所以对于由N次内积计算转换后的互相关运算，可以进一步利用FFT来改进。一般情况下，通过FFT算法计算互相关，不但不会对信号稀疏分解的效果产生任何影响，而且可以使稀疏分解过程中内积的计算速度至少提高一个数量级，从而大大提高信号稀疏分解的速度。

3 仿真与分析

本节采用过完备跳频信号结构字典与基于FFT改进的MP算法对跳频信号进行稀疏分解，并与文献［4］提出的Gabor过完备字典下的稀疏分解效果进行对比。其中，Gabor原子和跳频信号结构原子的波形分别如图1和图2所示。由于信号的重构和分解采用同样的方法，不同的是重构和分解为互逆过程。因此，采用对跳频信号进行分解之后的重构性能来衡量算法的分解效果。

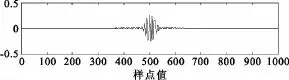
图1 Gabor原子波形Fig．1 Waveform of Gabor atom

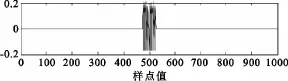
图2 跳频信号结构原子波形Fig．2 Waveform of FH signal structural atom

由于FSK与PSK是通信信号中最常用的两种调制方式，因此仿真中待分解的跳频信号采用FSK调制的跳频信号，其中信号长度 N=1 000，包含10个跳变频率，其中每跳包含100个采样点。跳频信号的跳变频率随着随机序列在200～2 000 Hz之间以200 Hz的间隔取值，采样频率为10 kHz，跳速为1 000跳/秒，信息速率为100比特/秒。跳频信号时域波形如图3所示。

对于上面的FSK调制跳频信号，分别对过完备的Gabor字典和文中提出的过完备跳频信号结构字典，采用FFT改进的MP算法对跳频信号进行稀疏分解，算法的执行结果分别如图4和图5所示。

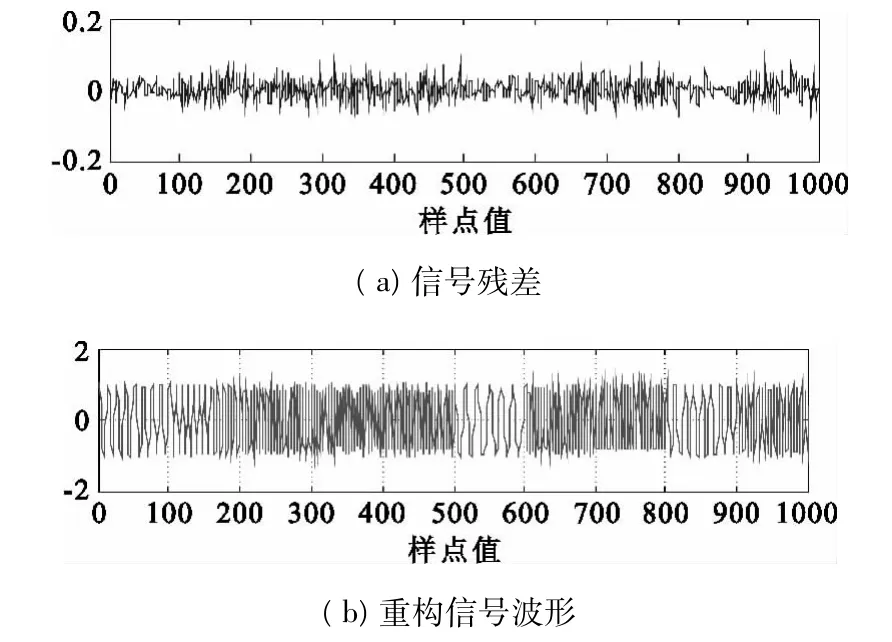
图4 Gabor字典下跳频信号分解及重构结果Fig．4 FH signal decomposition and reconstruction results under the Gabor dictionary

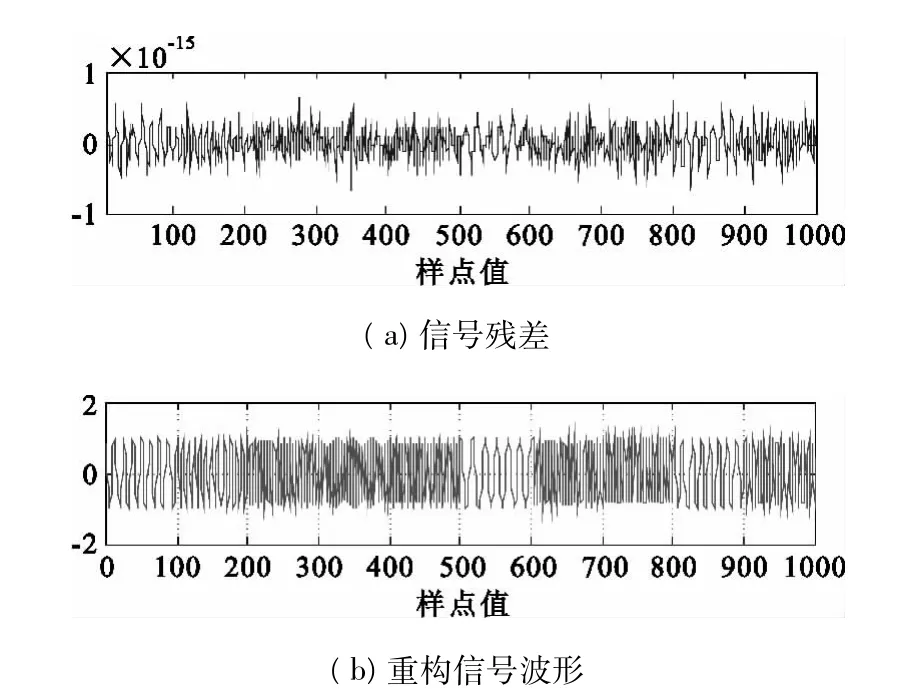
图5 跳频信号结构字典下的信号分解和重构结果Fig．5 FH signal decomposition and reconstruction results under the over－complete structural dictionary

图4(a)，图5(a)均为跳频信号分解得到的残差，信号残差随着迭代次数不断发生变化的，随着迭代次数的增加信号残差值就会变得越来越小;图4(b)，图5(b)均为重构之后的跳频信号波形。对图4(a)和图5(a)所示的信号残差波形进行比较可以看出，采用跳频信号结构字典对信号进行分解得到的残差幅度远远小于过完备Gabor字典下对跳频信号进行分解得到的残差幅度。因此，从信号分解残差的角度来说，基于过完备跳频信号结构字典的信号分解性能优于过完备Gabor字典下的信号分解性能。

由于信号重构和信号分解是采用相同的算法但却完全互逆的过程，因此利用信号的重构性能来评估过完备字典下的跳频信号稀疏分解性能是完全合理的。利用重构跳频信号的均方误差(MSE，Mean Square Error)来衡量算法的重构性能，均方误差表达式如下:

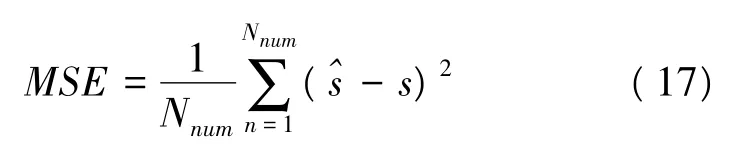
图6为跳频信号在两种过完备字典下进行稀疏分解之后再重构得到的均方误差性能曲线。

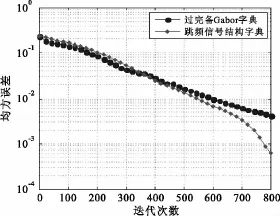
图6 不同过完备字典下的跳频信号分解后再重构的性能Fig．6 Reconstruction performance of FH signal under different over－complete dictionaries

由图6可以得到这样的结论:过完备Gabor字典和跳频信号结构字典均能够很好的对跳频信号进行稀疏分解，且分解效果较好;随着迭代次数的增加，信号稀疏分解效果越好，但是从最终的分解效果来说，文中提出的跳频信号结构字典下的分解性能要明显好于过完备Gabor字典下的分解性能。这也正好验证了之前由图4(a)和图5(a)的信号残差幅值所得到的结论。从图6还可以看出，当迭代次数为600时，均方误差性能均已达到了10－2数量级。

为进一步说明跳频信号结构字典下稀疏分解的优势，这里对不同过完备字典下的稀疏分解算法执行所需时间进行统计，如表1所示。

表1 跳频信号稀疏分解仿真所需时间Table 1 Simulation time for FH signal sparse decomposition

由表1可以看出，虽然两种过完备字典下的跳频信号稀疏分解能够得到相近的分解性能，但是跳频信号结构字典下的稀疏分解方法用时仅为过完备Gabor字典下的0．4%，提高了将近230倍。另外，由于跳频信号结构原子更加接近跳频信号的结构特性，生成的过完备字典中原子个数也将远远少于过完备Gabor字典中的原子个数。因此，生成一个过完备的跳频信号结构字典用时也将明显少于过完备Gabor字典。

综上所述，但是采用文中提出的跳频信号结构字典进行稀疏分解，可以大大减少跳频信号在稀疏表示环节所消耗的时间，从而为后续处理节省了大量时间。

4 结语

跳频信号具有特殊的结构特性。文中从跳频信号的自身结构出发，构造了更加接近其结构特性的跳频信号过完备结构字典，并利用基于FFT方法改进的MP分解算法研究了跳频信号在过完备时频字典下的稀疏分解。该方法对跳频信号的分解效果和分解所需时间两个方面都有了很大改善。后续的研究中希望能够更加充分地利用跳频信号的先验信息来构造过完备字典，而更加快速高效的稀疏分解算法也是一个值得关注的研究方向。

［1］ 梅文华，王淑波，邱永红，等．跳频通信［M］．北京:国防工业出版社，2005:2－7．MEI Wen－hua，WANG Shu－bo，QIU Yong－hong．Frequency Hopping Communications［M］．Beijing:National Defence Industry Press，2005:2－7．

［2］ 姚富强．通信抗干扰工程与实践［M］．北京:电子工业出版社，2012:26－29．YAO Fu－qiang．Communication Anti－Jamming Engineer－ ing and Practice(Second Edition)［M］．Beijing:Publishing House of Electronics Industry，2012:26－29．

［3］ 闫凤丹，于莲芝．基于小波变换的超声数据采集与处理［J］．通信技术，2013，46(09):68－71．YAN Feng－dan，YU Lian－zhi．Ultrasonic Data Acquisition and Processing based on Wavelet Transform．Communi－ cations Technology，2013，46(09):68－71．

［4］ 郭金库，刘光斌，余志勇，等．信号稀疏表示理论及其应用［M］．北京:科学出版社，2013:22－30．GUO Jin－ku，LIU Guang－bin，YU Zhi－yong et al．Signal Sparse Representation Theory and Its Application［M］，Beijing:Science Press，2013．pp．22－30．

［5］ MALLAT S，ZHANG Z．Matching Pursuits with Timefrequency Dictionaries［J］．IEEE Transactions Signal Process，1993，41(12):3397－3415．

［6］ 张春梅，尹忠科，肖明霞．基于冗余字典的信号超完备表示与稀疏分解［J］．科学通报，2006，51(06):628－633．ZHANG Chun－mei，YIN Zhong－ke，XIAO Ming－xia．Redundant Dictionary Based Signal Over－complete Representation and Sparse Decomposition［J］．Chinese Science Bulletin，2006，51(06):628－633．

［7］ LASKA J，KIROLOS S，MASSOUD Y，et al．Random Sampling for Analog－to－information Conversion of Wideband Signals［C］//Design，Applications，Integration and Software，2006 IEEE Dallas/CAS Workshop on．Richardson，TX:IEEE，2006:119－122．

［8］ 尹忠科，邵君，Pierre Vandergheynst．利用FFT实现基于MP的信号稀疏分解［J］．电子与信息学报，2006，28(04):614－618．YIN Zhong－ke，SHAO Jun，PIERRE Vandergheynst．MP Based Signal Sparse Decomposition with FFT［J］．Journal of Electronics＆ Information Technology，2006，28(04):614－618．