基于拍卖博弈的资产剥离实物期权决策＊

梁 铄 陈 静

（中国海洋大学 管理学院，山东 青岛266100）

一、引言

并购重组是企业重要的战略行为。并购重组决策具有环境不确定、时机可选择、成本不可逆等特性，因而适于用期权方法进行研究。Smith和Triantis最早对战略收购的实物期权特性进行了分析，指出恰当的时机选择会提升并购价值。［1］由于并购重组过程至少涉及两个利益主体，单纯的实物期权分析无法刻画利益主体之间的博弈关系，因而近年来以博弈论和实物期权为主体的期权博弈方法逐步兴起，在并购重组研究中占据了越来越重要的地位。Smit最早提出了一个在制定战略收购计划中应用实物期权理论与博弈理论的框架，并指出实物期权理论与博弈论的定量方法与来自战略管理的定性方法结合可为并购过程提供更好的决策。［2］Lambrecht、Morellec和Zhdanov、Mason和 Weeds、扈文秀、郑湘明和陈晓红、陈珠明等分别从出价竞争、不完全信息、规模经济、并购溢价、产品竞争、市场趋势等多个角度对这一领域的研究进行了拓展。［3－9］

目前基于期权博弈的并购重组研究大多关注并购决策，但对于资产剥离这一并购重组的另一重要主题则关注不够。资产剥离行为在中外资本市场上大量发生。如在中国，资产剥离是上市公司仅次于收购兼并的第二大重组方式，自l998年以来一直占整个上市公司资产重组活动的20%以上，某些年份更是占到企业重组总数的40%以上。［10］而在美国自1975年之后的近30年间，资产剥离交易占当年全部交易的35%～40%。［11］（P5－10）此外，资产剥离是并购的前端问题，对剥离决策的充分研究有助于对并购行为的理解。Myers和Majd、Berger等、Choi和Lee、Clark和Rousseau较早利用基本实物期权模型研究了拟剥离资产价值固定与随机变化等不同情况下资产剥离的时机决策问题。［12－15］近年来的文献开始考虑剥离利益主体间博弈关系。Lambrecht和Myers考虑了存在委托代理、债务融资、外部接管等情景下的资产剥离决策。［16］梁铄等研究了委托代理双方信息不对称以及买卖双方进行讨价还价博弈等情景下的资产剥离决策。［17-18］

根据买方市场的竞争程度，实践中资产剥离的交易方式一般可分为二手市场直接销售、议价交易、拍卖等三种。直接销售适于完全竞争的二手资产市场，讨价还价适于买方非常稀少的二手资产市场，这两种情况在现实中并不普遍。更普遍的是，某种资产的二手市场有一定数量的买家，但竞争并不充分。在这种情况下，资产剥离往往采用拍卖的形式进行交易。现有文献大都是在剥离交易采用二手市场直接销售的假设下进行研究，但是对于以拍卖形式进行剥离交易的问题，还没有文献关注。本文利用博弈论中的拍卖模型刻画拍卖交易，研究在不确定环境下资产剥离的时机选择问题。建立了实物期权模型，证明了其解的存在性和唯一性，并进行了算例分析。目的是为实践中企业选择剥离时机及交易方式提供理论依据。

二、模型设定

企业有某项资产需要剥离，拟剥离资产价值为该资产未来创造各期现金流的贴现值。由于环境不确定性，其价值V服从几何布朗运动：

式中，α为资产价值运动的漂移率，本文假设其小于0以反映资产价值逐渐减少的趋势；σ＞0为资产价值运动的波动率；dz为布朗运动的增量过程。由于0是随机过程的一个吸收壁，因此假设期初资产价值V0＞＞0。假设剥离交易的买卖双方均为风险中性，所要求的无风险收益率为μ。令δ＝μ－α＞0表示该资产的回报不足，它表达了企业持有该资产的机会成本。由于该资产具有专用性，价值V只对企业自身成立，企业无法按这一价值进行剥离交易。

在资产剥离时，企业将通过拍卖的方式出售该项资产，拍卖获得的收益为资产回收价值。为简化分析，假设拍卖过程具备对称、独立的私人估价模型（SIPV）的特征，即所有投标者同质，其私人估价服从独立同分布的连续随机变量，每个投标者都知道自己的估 价，但 其 他 人 不 了 解 他 的 估 价。［19］（P191－201）该资产只能作为一个整体进行拍卖，拍卖过程瞬时完成且不发生成本。拍卖方与剥离方表示同样含义，在后文根据语境需要交替使用。

设拍卖中共有n位投标者，代表性投标者i的估价为vi，服从区间［0，珔v］上的均匀分布U（vi）。由于所有投标者独立且同质，其估价的概率分布为独立同分布，因此投资者估价的联合分布函数为U（v1）U（v2）…U（vn），即所有单个投标者估价分布函数的乘积。投标者的战略是他们的投标函数bi，在投标者同质的情况下存在对称均衡，即所有投标者的战略都相同，均为bi＝b（vi）。假定只要投标者的估价不低于保留价格Vd＞0便愿意参与拍卖，保留价格Vd是剥离企业规定的最小投标价，等于企业在剥离时的资产价值①最 优拍卖机制设计还需考虑保留价格的最优设定问题，但这一问题与最优时机选择结合在一起使整个问题过于复杂，且实践中难以做到保留价格的最优设定，故本文从实际出发做这一假设。。

拟剥离资产的价值受不确定环境的影响随机波动，而其回收价值由剥离时的拍卖过程决定，因此企业资产剥离的核心决策，在于选择适当时机进行拍卖。对企业而言，这是一个无到期日的美式卖权。根据美式卖权的特性，选择适当的时机等价于选择一个适当的临界值，当资产价值达到这一临界值时进行拍卖，可 使 拍 卖的收益最大 化。［20］（P116－128）一 旦进入拍卖过程，这一临界值即成为剥离企业规定的最小投标价，也即保留价格Vd。企业要制定最优的资产剥离决策，首先要估计拍卖时所能获得收益，这需要利用拍卖博弈的框架进行分析。之后企业根据这一预期收益确定最优剥离时机，即确定一个适当的资产价值临界值。以下逐步进行讨论。

三、拍卖的预期收益

对称、独立、私人估价拍卖（SIPV）已经得到了充分的研究，在此分析框架下容易证明：①所有把最高投标者作为赢者，有对称均衡和相同保留价格的拍卖，都产生相同的均衡支付，即拍卖所采用的形式无关紧要。②均衡的投标函数b＊（v）严格单调递增，估价高于Vd的投标者在拍卖中赢标的概率是U（v）n－1，且投标者的预期支付额为：［19］（P191－201）

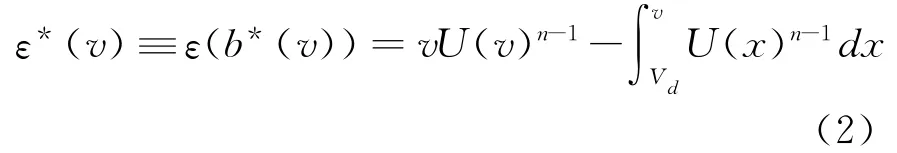
式中右边第一项为投标者预期收入，即所购资产对其自身的价值乘以竞标成功的概率，第二项为投标者参与拍卖的预期利润函数，两项相减即为投标者的预期支付额。这也是对于拍卖者而言，从单个竞标者获得的预期收入。

拍卖者从单个投标者能够获得的收益则还要从上式中扣除成本：

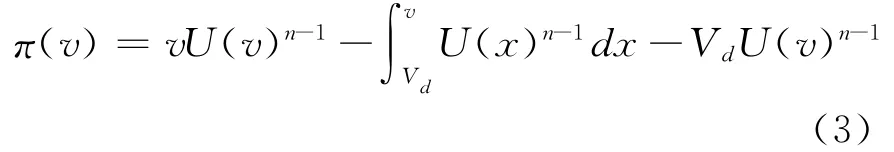
即从单个竞标者获得的预期收入中扣除拍卖者需支付的成本的期望值VdU（v）n－1，其中Vd为拍卖时资产对于拍卖方的价值，U（v）n－1为单个投标者成交的概率。因为不了解投标者的估价，拍卖者只能求投标者的预期支付的期望值。把从n位投标者获得的预期收益的期望值相加，便得到拍卖者总的预期收益②拍卖者求投标者预期支付的期望值时需运用顺序统计量，具体分析过程可参考文献［19］。：

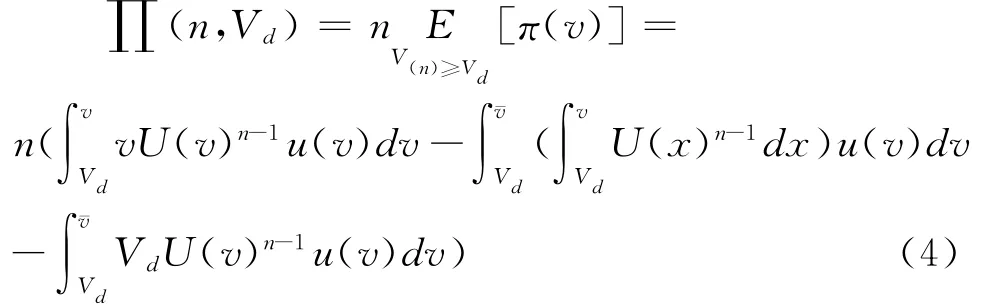
利用分部积分法变形并化简可得：

四、剥离决策

式（5）给出了企业在拍卖时的预期收益，它是拟剥离资产价值的函数。在真正将资产剥离之前，企业持有一个将资产剥离的无到期日美式卖权。运用标准的或有要求权分析法（CCA）及Ito定理，可以得到该剥离期权价值F（V）所满足的二阶微分方程：［21］（P127-142）

边界条件：

式中V＊表示待求的执行剥离决策的最优资产价值临界值。一旦进行剥离，则根据前文假设这一价值即成为剥离方的保留价格Vd。V＊和Vd两者数值相同但其涵义不同，因而用不同符号分别表示。边界条件（6．1）表明，当资产价值为无穷大的时候，剥离期权将不具有价值，因为此时剥离发生的概率趋于0；边界条件（6．2）为价值匹配条件，给出了拍卖时的预期收益；边界条件（6．3）是平滑粘贴条件，表明期权价值函数在执行边界处光滑连续。最优剥离时机选择问题转化为寻找执行剥离的最优临界值V＊。

满足边界条件式（6．1）的微分方程通解为：［21］（P127－142）

其中，A为待定参数，β2为微分方程（6）的特征方程0．5σ2β（β－1）＋αβ－r＝0的负根。将通解代入边界条件式（6．2，6．3），得到如下方程组：

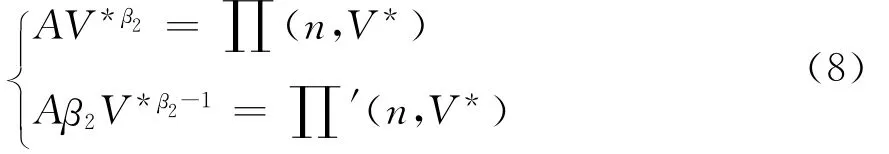
将均匀分布的密度函数与分布函数带入拍卖者利润函数∏（n，V＊）并化简得到：

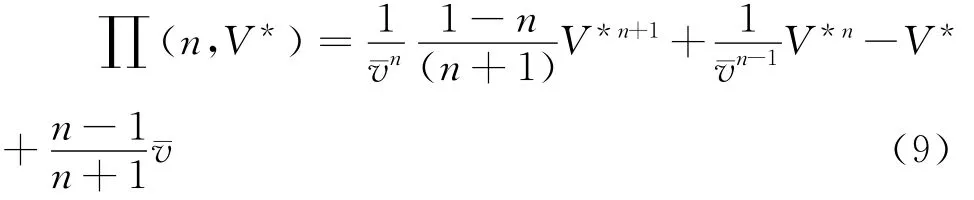
代入方程组（8）后得到：

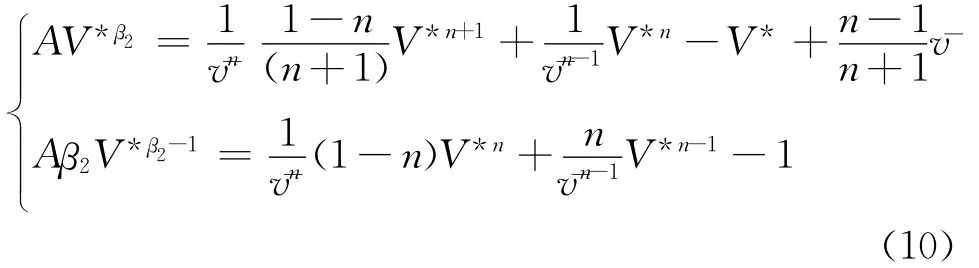
上式为2元n＋1次方程组，待求的未知数为V＊和A。将两式联立化简并消掉A可得：

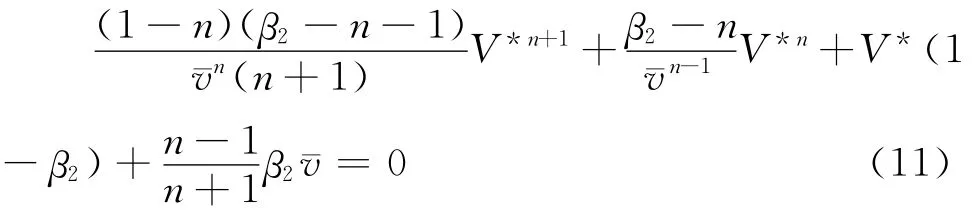
上式为一元n＋1次方程，待求未知数为V＊，在n＞3的情况下，该方程一般无法用解析的方式求解，但可以证明，在问题的经济可行域（0，珔v）内，该方程存在唯一解（证明请见附录）。因此可利用数值求解方法，如牛顿法、二分法等，［22］（P40－50）在可行域内解出V＊。之后，可将V＊值带回方程组（10）求出参数A的值，并进而利用式（7）求出资产剥离期权的价值。企业的资产剥离策略即可根据求得的V＊值制定，当V＞V＊时，等待时机；而当V＝V＊时，进行资产拍卖。此时资产价值V＊为该资产对于剥离方的价值，也是剥离方在拍卖时的保留价格Vd。

五、对n取不同极端值的分析

（一）当n趋于无穷大时

当竞拍人数n趋于无穷大时，买方市场趋近于完全竞争。将拍卖者利润函数（9）对n求极限可以得到：

将上式代入边界条件（6．1－6．3），则边界条件退化为：

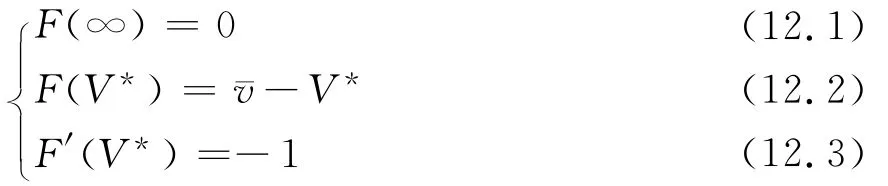
这表明当市场趋近于完全竞争时，资产交易价格将是珔v，卖方接受市场的定价，以这一固定价格出售资产，此时剥离决策问题退化为最基本情况。［12］由于竞拍人数增多加剧了竞争，成交价格会随着竞拍人数的增加而上升，这有利于拍卖方。

（二）当n等于1时

当买方人数等于1时，交易在买卖双方之间进行，事实上已经不符合拍卖的定义，但仍加以分析以便进行比较。令（9）式中的n＝1得到：

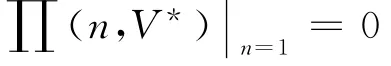
此时卖方的收益为0，交易的价格为拟剥离资产对于剥离方的价值，买方获得交易的全部剩余。这是由于在本文设定的拍卖交易框架中，卖方只是提出一个保留价格，并不因为其唯一性而获得垄断收益。而买方却由于其唯一性在交易中获得完全垄断的地位，因而取得全部交易剩余。由于拟剥离资产的交易价格与它对剥离方的价值一样，剥离期权对于剥离方而言价值为0。根据式（11），此时V＊取值可以为问题经济可行域内的任意值，并不存在时机选择问题。不过在现实中，如果买方只有一个人，卖方并不会采用拍卖的方式进行交易，而会采用讨价还价的交易方式。讨价还价的交易方式隐含了交易双方为双边垄断的假设，买卖双方的讨价还价能力决定了利益的分割。梁铄、唐小我研究了基于讨价还价交易的资产剥离实物期权决策，得到了资产剥离的临界值及交易双方的期权价值公式。［18］

（三）不同交易方式的比较

根据上述分析，当n比较大时，剥离方会选择拍卖的形式进行交易，以尽可能利用买方之间竞争获得更高卖价，如果利用讨价还价方式进行交易则会损害价值。当n＝1时，剥离方自然会选择讨价还价的交易方式。但当买方人数较少时，由于基于拍卖模型的解析解难以取得，选择哪种交易方式能给剥离方带来更高收益则难以判断。不过在参数已知的情况下，总可以通过数值解比较出两者对于剥离方的优劣。

六、数值分析

（一）基本参数

由于期权价值和临界值函数复杂，难以用解析的方式研究其性质，故采用数值分析的方式进行研究。根据问题的实际经济意义选择以下一组参数值，并作为后面参数敏感性分析的基础。

表1 数值分析参数赋值

将上述数据代入式（11），利用数值方法对其求解（本文利用Excel的“单变量求解”功能），可以得到资产剥离的临界值V＊为2．13。将该值代入式（10），可求得 A为7．89。最后利用式（7），可得到资产剥离期权F（V＊）的价值为2．75。

（二）参数敏感性分析

以下分别对σ、α等进行参数敏感性分析，即在保持其他参数不变的情况下，考察某个参数在合理区间内变动对于资产剥离期权价值和剥离临界值的影响。

图1 资产价值运动参数敏感性分析

波动率σ和漂移率α刻画了拟剥离资产价值运动的特性。由图1左图可发现，当资产价值波动性σ提高时，剥离期权的价值增加而剥离临界值下降。这是由于波动率增大会使剥离的预期收益增加。在贴现率一定的情况下，这增大了剥离期权的价值，并允许有更长的等待时间。图1中间图显示了随漂移率α上升，剥离期权的价值在下降，而剥离临界值在上升。漂移率α上升反映了资产价值下降趋势减缓，资产被剥离的可能性减小，由剥离获得的收益也会减小，因而剥离期权价值下降。图1右图显示随无风险利率μ上升，剥离期权的价值下降而剥离临界值上升。这是由于当无风险利率提升时，剥离交易的贴现值会减小，因而剥离期权的价值减小。此外由于等待的机会成本变高，更早的剥离变得有利，这提升了剥离临界值。总体来看，这些结果与标准美式永久卖权对应的分析结果一致。［20］（P138-151）

图2 拍卖交易参数敏感性分析

买者估值上限珔v与拍卖参与人数n是刻画拍卖交易的两个重要参数。由图2左图可以发现，随着买方估值上限珔v的提升，资产剥离期权的价值与剥离临界值都在提升。这是由于随估值上限的提升，买方的期望出价会更高，被剥离资产拍卖的成交价格也会更高，这显然会提高剥离收益，进而提升剥离期权的价值。这种情况下等待会使由贴现造成的损失加大，因而等待时间应当缩短，即资产剥离临界值提高。买方人数n增加的效果与估值上限提升的影响类似。随买方人数增加买方出价竞争会更激烈，这同样会使被剥离资产拍卖的成交价格上升，并进而提高剥离交易收益、剥离期权价值与剥离临界值。

七、结论

本文研究了不确定环境下，采用拍卖方式进行资产剥离的实物期权决策问题，具有重要的实践应用价值。对于实际企业而言，当面临以拍卖方式进行剥离交易的决策时，本文提供的分析方法不但比传统基于贴现现金流的方法要合理，也比基于普通美式卖权的决策要准确，并且应用方便，利用流行的办公计算软件如Excel即可完成分析。因而可为实践中企业决定剥离时机及交易方式等提供理论指导。

本研究对于证券市场投资者的应用价值在于，对于上市公司中处于下降趋势的业务部门或资产，可从其资产专用性、潜在购买者的数量、估值范围等角度考察拟剥离业务部门或资产买方的潜在竞争结构，进而估计资产剥离交易的形式。对于可能采用拍卖形式进行剥离交易的企业，可利用本文提供的方法判断剥离交易时机及剥离对于企业价值的提升，进而以之为基础制定投资策略，获得超额回报。

对本文的拓展可从以下方面进行。一是对于拍卖形式的设定。本文在SIPV框架下分析了剥离交易，而实践中买者的非对称、买者间估值相关性，甚至串谋等因素都会对拍卖过程产生影响，这需要放松本文假设进一步研究。二是拍卖参与人数的确定。在本文的设定中，剥离交易之前企业已知道买方人数，这一假设较强，进一步的假设应当是参与拍卖的人数为随机变量。此外，本文假设被剥离资产对于买者的价值确定，一个可能的拓展是考虑被剥离资产价值对买者来说不断变化，从而将拍卖置于连续时间框架下。

附录

证明方程（11）在经济可行域（0，珔v）内有唯一解。

证明：方程（11）如果有解的话，则解必在区间（0，珔v）内，这是由于方程的解是资产剥离交易价格，卖方不可能将价值为正的资产卖出小于等于0的价格，买方也不可能按大于等于对资产估值上限的价格进行购买。称区间（0，珔v）可为解的经济可行域。

解的存在性：由上述结果知，在可行域的左边界U（v0）小于0，在可行域右边界，U（v0）等于0，其一阶导数为0，二阶导数为正。可知U（v0）在可行域右边界邻域内取极小值0，因而U（·）在右边界的左临域内大于0。由于U（v0）为连续函数，因此在可行域内必存在U（v0）＝0的点。

解的唯一性：函数区间为（上）凸函数，在凹（下凸）函数利用反证法，假设U（v0）在可行域内与横轴有两个交点，则随v0增大第一个U（v0）＝0点导数为正，第二个交点导数为负。这使得U（v0）在右边界处由下向上与横轴相交，这与U（v0）在右边界左邻域大于0矛盾。由曲线在可行域内拐点个数知，U（v0）与横轴相交次数不可能大于2。

综上所述，U（v0）＝0在可行域内有唯一解。证明过程可参考图3。

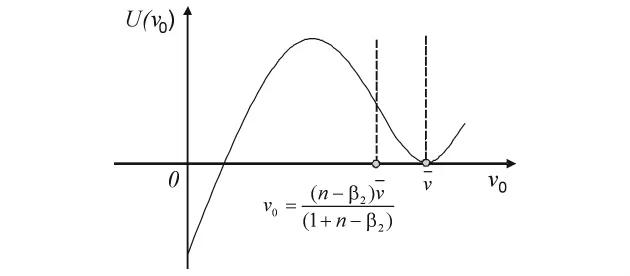
图3 解的存在性与唯一性证明示意图

［1］Smith K，Triantis A．The value of options in strategic acquisitions［A］．Trigeorgis L．Real Options in Capital Investment：Models，Strategies，and Applications［C］．New York：Praeger，1994．

［2］Smit HTJ．Acquisition strategies as option games［J］．Journal of Applied Corporate Finance，2001，14（2）：79-89．

［3］Lambrecht B．The timing and terms of mergers motivated by economies of scale［J］．Journal of Financial Economics，2004，72：41-62．

［4］Morellec E，Zhdanov A．The dynamics of mergers and acquisitions［J］．Journal of Financial Economics，2005，77：647-672．

［6］Robin Mason，Helen Weeds．The timing of takeovers in growing and declining markets．Centre for Economic Policy Research（CEPR，UK）Discussion Paper，2010，NO．DP7678．

［7］扈文秀，边璐，张江朋．基于不完全溢价信息的并购时机期权博弈研究［J］．运筹与管理，2010，19（6）：86-92．

［8］郑湘明，陈晓红．基于非完全信息期权博弈的企业并购决策时机［J］．系统工程，2011，29（7）：81-84．

［9］陈珠明．企业控制权转让的最优时机与均衡价格［J］．上海交通大学学报，2011，45（1）：105-109．

［10］苏文兵，李心合，莫迁．多元化程度、经理人变更与企业资产剥离—来自中国上市公司的经验证据［J］．财贸研究，2009，（6）：89-96．

［11］高根．兼并、收购与公司重组［M］．北京：机械工业出版社，2004．

［12］Myers SC，Majd S．Abandonment value and project life［J］．Advances in Futures and Options Research，1990，（4）：1-21．

［13］Berger PG，Ofek E and Swary I．Investor valuation of the abandonment option［J］．Journal of Financial Economics，1996，49：257-287．

［14］Choi YK，Lee SW．Investment and abandonment decisions with uncertain price and cost［J］．Journal of Business Finance ＆ Accounting，2000，（1）：195-213．

［15］Clark E，Rousseau P．Strategic parameters for capital budgeting when abandonment value is stochastic［J］．Applied Financial E-conomics，2002，（12）：123-130．

［16］Lambrecht BM，Myers SC．A theory of takeovers and disinvestment［J］．Journal of Finance，2007，62（2）：809-845．

［17］梁铄，唐小我，马永开．基于实物期权方法的信息不对称下资产剥离决策研究［J］．系统工程理论与实践，2007，（6）：36-42．

［18］梁铄，唐小我．基于讨价还价的资产剥离实物期权决策［J］．科技管理研究，2009，（12）：297-300．

［19］Elmar Wolfstetter．高级微观经济学——产业组织理论，拍卖和激励理论［M］．上海：上海财经大学出版社，2003．

［20］姜礼尚．期权定价的数学模型和方法［M］．北京：高等教育出版社，2003．

［21］Dixit AK，Pindyk RS．不确定条件下的投资［M］．北京：中国人民大学出版社，2002．

［22］马东升，雷勇军．数值计算方法（第2版）［M］．北京：机械工业出版社，2007．