基于二阶系统解耦对非奇异解的研究
张善美,许 峰
(安徽理工大学 理学院,安徽 淮南232000)
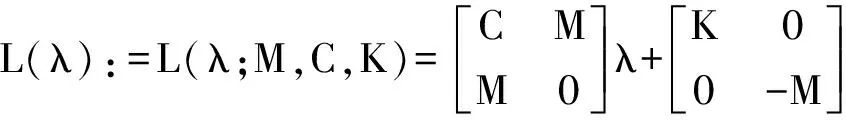
对于L(λ)进行变换求解
令
这里其中MD、CD和KD都为M、C、K的n×n的对角型矩阵[1],由此可以看出A与B是2n×2n阶矩阵Brierley[2]给出了A,B是同维数矩阵情况下,方程AX-XB=C解的一种显式表达.邱海明等人[3]在A,B不同维情况下,给出方程解AX-XB=C的4种显式表达,戴华[4]求解出的积分形式,但关于这类方程的求解均比较复杂,而且一般都引入了其他参量.
本文根据齐次AX+XB=0方程解的一种构造方法求得其非奇异解,即基于系统解耦前后具有相同谱信息来构造通解的形式,从而通过参数估计的方法找到非奇异解.为求解齐次AX+XB=0方程的非奇异解问题找到了一种简便可行的方法.
1 λs+λt≠0时Yst为零矩阵
定理1 对于任意的AX+XB=0形式的矩阵方程,可将其化为JY+YJ=0的形式,这里J为若当标准型,Y为可逆矩阵,当λs+λt≠0且Y中的每个小块Yi为零矩阵(J的每个若当块Ji,Y与J分法相同,λi为J的特征值).
证明由于X为可逆矩阵
AX+XB=0
可以写为
X-1AX=-B
则A与-B有相同的谱信息,即特征值相同,可以通过相似变换找到相同的若当标准型
Y-1JY=-J
这里
所以
AX+XB=0可以写成JY+YJ=0的形式.
即
有
(1)
若二阶系统中的矩阵为n×n阶,则AX+XB=0中的A与B是2n×2n阶矩阵,由式(1)中分块矩阵对应相等有
JsYst=-YstJt
(2)
这里的λsIks+Nks为对应特征值λs(1≤s≤p)的Ks阶Jordan块,Nks为Ks阶位移幂零Jordan块将Js=λsIks+Nks,Jt+λtIkt+Nkt代入式(2)有
(λs+λt)Yst=ystNkt-NKsYst
(3)
用(λs+λt)乘上式两边:
其中:λs+λt≠0.

(λs+λt)rYst=O
由于λs+λt≠0则Yst=0,即Y中所有非对角块中元素均为0.
根据JsYst=-YstJt有
有第一列对应等式
得a11,a21,…,as1=0如此计算后面列方程有a21,…a2s,…,as1,…,ass=0所以有Yst=0
2 λs+λt=0时Yst的形式
定理2对于JY+YJ=0的形式矩阵,这里J为若当标准型,Y为可逆矩阵,其中λsIks+Nks为对应特征值λs(1≤s,t≤p)的Ks阶Jordan块,ks=kt时,且当λs+λt=0时Yst为上三角矩阵.
证明当λs+λt=0时,式(3)可变成
-YstNkt=NksYst
(4)
由于Nks为Ks阶位移幂零阵,可以设,
根据式(4)可以写成
有第一列对应等式a21,…,as1=0如此计算后面列方程有a32,…,as2,……as,s-1=0

所以当ks=kt时,且当λs+λt=0时Yst为上三角矩阵.
接下来讨论当λs+λt=0且ks 对应解得 同理当λs+λt=0且ks>kt时,Yst的构造 综上所述,1)对于由二阶系统变化的AX+XB=0先将其变为YY+YJ=0 2)按照J的分法将Y分成小块Yst,按照分法构造Yst,若λs+λt≠0时Yst=O; ks=kt时,且当λs+λt=0时Yst为上三角矩阵. ks 3)根据构造方法,将参数赋值后找到非奇异的Y,因此,根据X=EYF-1(E,F,均为可逆矩阵)即能得到非奇异的X. 本文根据齐次AX+XB=0方程解的一种构造方法求得其非奇异解,即基于系统解耦前后谱信息相同来构造通解的形式,从而通过参数估计的方法找到非奇异解.下面给出2个例子: 数值试验1: 根据A和B的定义,有 根据构造方式: 由于E跟F均为可逆矩阵,即当a,b,c,d取任意非零数即可得到非奇异的X,根据文献[5-6]的构造方法,得 B= 经计算得,JB=F-1BF=-JA 如当a,b,c,d分别为1,-4,7,9时, X=EYF-1= 则 ≈0 则,B=-X-1PX 数值试验3: 由于E跟F均为可逆矩阵,即当a,b,f取任意非零数即可得到非奇异的X.根据文献[5]的构造方法,得 如当a,b,c,d,f分别为1,3,4,4,-1时,有: 即B=-X-1PX 通过上面2个实例,对于齐次AX+XB=0求非奇异解问题,可以直接构造出解的形式,然后根据这种形式就可以找到非奇异解,相比于直接用线性方程组求解,这样的构造方法可以大大减少计算量,并且可以更加简便的找到非奇异解. 对于求解解耦变换的非线性问题转化为求奇次AX+XB=0方程的非奇异解可以有效地解决二阶系统的解耦问题.本文根据二阶系统通过Lancaster结构,即系统解耦前后具有相同谱信息进行通解形式的构造到一个非奇异解. 参考文献: [1] GARVEY S D, FRISWELL M I, PRELLS U. Co-ordinate transformations for second order systems, part I: general transformations [J]. J. Sound Vib., 2002, 258(5):885-909. [2] BRIERLEY S D, LEE E B.Solution of the equationA(z)(Z)+ (Z)B(z)=C(z) and its application to the stability of generalized linear system [J]. Int J Control, 1994, 40(6): 1065-1075. [3] 邱海明, 付明义. 关于方程AX+XB=C的解法[J]. 控制与决策, 1989, 4(2): 769-776. [4] 戴 华. 矩阵论[M]. 北京: 科学出版社, 2005.248-263. [5] 张善美, 沈继红. 二阶系统解耦中齐次Sylvester方程非奇异解求解[J]. 哈尔滨商业大学学报:自然科学版, 2011,27(6): 849-853, 892. [6] 张善美,沈继红.一类关于Sylvester方程特殊形式的解[J].哈尔滨商业大学学报:自然科学版,2013,29(6):734-740.

3 数值实验









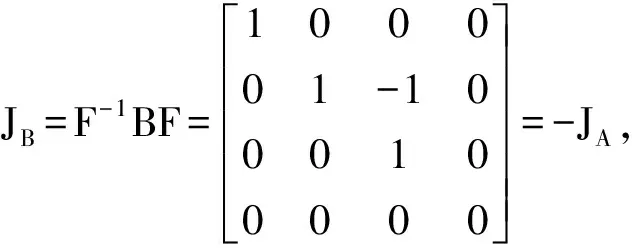



4 结 语

