Exact boundary controllability on a class of variable coefficients wave equation

LI Da-mei, XIE Wei-song

(Department of Mathematics, Tianjin University, Tianjin 300072, China)

1 Introduction

Exact boundary controllability of wave equation has received considerable attention in the literature. Numerous contributions have been achieved over the past several years[1-5].The control of hyperbolic system can be interior control acting on whole or part domain of the solutions and also can be boundary control acting on the boundary of the solving domain. However, it is often rather difficult to analyze the interior controllability in practical application[6-10]. In this paper, we will study exact controllability of the wave equation through boundary control which is assumed to act on a subset of the boundary. In the sequel, we will research a specific but important example since it concerns the exact boundary controllability of wave equation. Now, consider the evolution system

(1)

(2)

for someα>0 and for allζ=(ζ1,ζ2,…ζn)∈nLet Ω be a non-empty bounded open domain ofn,Γbe its boundary withTa given positive number, and set

(u0,u1)∈L2(Ω)×H-1(Ω)

(3)

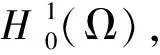
The exact boundary controllability of system (1) means trying to find a control functionu=vonΓ×

(4)

Concerning the exact controllability of system (1), we note that the caseaij=δija(t) is studied[11], and the caseaijwhich is independent of the timetis studied[7]. Now, we analyze the systems in a general case from the theoretical aspects. The objective of this paper is to show that this system is exactly controllable in the general case. We use the HUM introduced by Lions[8].

2 Description of HUM

In this section, we will describe the HUM briefly for exact boundary controllability of the variable coefficient wave equation from a part of the boundary. A brief summary of the relevant definition and some preliminary results are presented which will be used in this paper[12-17].

Let

Define the operatorΛ:F→F′ For any fixedx0∈Rn,we use the following notation

R=sup{|x-x0|:x∈Ω}=‖m(x)‖L∞(Ω),

Γ-={x∈Γ:m(x)·v(x)≤0},Γ+=ΓΓ-={x∈Γ:m(x)·v(x)>0},

(5)

wherev(x)=(v1(x),v2(x),…vn(x)) is the outward unit normal vector Γ.to Now letγ,β>0 andλ≥0 are real number, such that

(2aij-mk∂kaij)ζiζj≥γαijζiζj∀(x,t)∈Ω×+,

(6)

(mkζk)2≤βαijζiζj∀(x,t)∈Ω×+,

(7)

(8)

for allζ∈RnBy condition (2), and notice thataij∈W1,∞(Ω×+)isaboundedset,thenβandλalwaysexist.

Assume

(9)

andletT∈+suchthat

(10)

(11)

3 Exact boundary controllability of the variable coefficients wave equation

WestartwiththefollowingLemmasfortheproblemofexactboundarycontrollability[19-21].Lemma3.1.Theenergyofthesolution(11)definedbytheformula

(12)

isapositivefunctionandsatisfiestheidentity

(13)

Moreover,thereexistsλ≥0suchthat

(14)

e-λtE(0)≤E(t)≤eλtE(0), ∀t∈+

(15)

Proof.ByGuesmia[1], (13)canbeobtained.Accordingto(8), (12)and(13),wecanobtain(14).ByGronwall'sinequalitywecandeduce(15)from(14).Therefore,thelemmafollows.

Remark.Accordingtotheidentity(13),thesystemweanalysedisnotconservativeingeneralsincetheenergyisnotaconstantfunction.Thentheobservabilityinequalities(16)belowaregenerallymoredifficulttoachievethanthatofconservativesystems[22-23].

(16)

(17)

Usingthesymmetryofaijweobtainthat

(18)

Multiplying(17)by2,andintegratingbyparts,wededucethefollowingidentity

(19)

Usingthecondition(2),theestimate(15)andtheassumptionhk∈W1,∞(Ω),aij∈W1,∞(Ω×+)weknowthattheright-handsideof(19)canbeeasilymajorizedbycE(0)wherecisapositiveconstantnumber.What'smore,wecandeducefromthehomogeneousDirchletboundaryconditionin(11)that

φ=φ′=0,∂kφvi=∂vφvk,x∈Γ

Therefore,

hk∂kaij∂jφvi=(h·v)aij∂iφ∂jφ.

Hence,theleft-handsideof(19)isequalto

Ifwechooseh(x)suchthath(x)=v(x)onΓthenthesecondinequalityin(16)followswithc2=c.

Ifwechooseh(x)=m(x),theidentity(19)reducesto

Furthermore,wecanalsodeducefrom(11)that

Therefore,accordingto(2.1)-(2.2)and(3.1),wehave

(20)

Majorizingthelastintegral,wehave

(21)

Thenwecandeducethefollowinginequalityfrom(20)-(21)

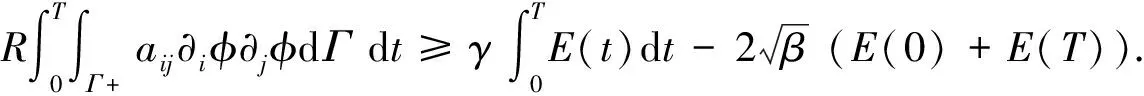
(22)

SupposeE(T)≥E(0),from(14),wehave

Therefore,from(22)wecanfurtherget

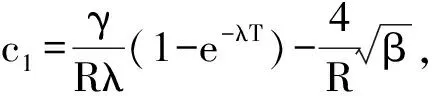
Similarly,wecanobtainthecaseforE(T)≤E(0)TheproofofLemma3.2iscompleted.Remark. (16)iscalledobservabilityinequalities.Lemma3.2meansthatinsomesensetheobservationofthesolutioninaneighbourhoodoftheboundaryduringasufficientlylargetimeallowsonetodeterminetheinitialdate.

Nowwegiveanequivalentformoftheintegralin(16).

(23)

Proof. According to the homogeneous Dirichlet boundary condition in (2.7), we have，

∂kφvi=∂vφvkvi=∂iφvkonΓ,

(24)

Concerning the first inequality in (23), and (24), we can further obtain

therefore,

αaij∂jφ∂iφ≤|aij∂iφvi|2

For the second inequality in (23),

Hence, the proof of Lemma 3.3 is completed.

Applying HUM, we can deduce an exact controllability result of system (1) from the above lemmas.

(25)

Proof. Consider the following system

(26)

It is well known that system (26) has only one solutionΨ∈C(R+;L2(Ω)) . Multiplying (11) by integrating byΨparts formally, and applying Green's formula, we obtain

According to system (11) and (26), we obtain

Hence, settingΛ(e0,e1)=(Ψ′(0),-Ψ(0)) for brevity, we have

(27)

Obviously,Λ:F→F′is a bounded linear map. Indeed, for any given(u0,u1)∈L2(Ω)×H-1(Ω)it will suffice to choose the controlv, and takedefined by the boundary condition of (26), whereφis the solution of (11) corresponding toΛ(e0,e1)=(Ψ′(0),-Ψ(0))and functionΨdefined in system (26) satisfies (Ψ′(0),-Ψ(0))=(u0,u1)By uniqueness of solutions for linear hyperbolic systems, we conclude thatu=Ψand from (26), we obtain the result (25). Therefore, proof of Theorem 3.1 is completed.

Applying Lemmas 3.1-3.2, we conclude from the identity (27) thatΛis a strongly elliptic operator fromFontF′ofor sufficiently large values of(Strongly elliptic is used as coercive, sinceis not a partial differential operator).

Theorem 3.2. Operatorused in Theorem 3.1 is a self-adjoint operator.

In the above formula,〈.,.〉 denotes the duality pairing betweenF′andF.Then we canfurther obtain that

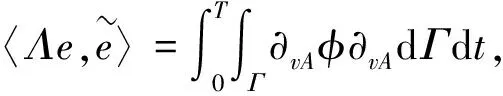
(28)

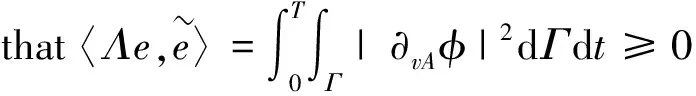
4 Conclusions

In this paper, the case of exact control on a part of the boundary is analyzed more precisely. Furthermore, we prove that the above system is exactly controllable when is large enough. According to the above analysis, some important theoretical results are presented. Moreover, we obtain an improved understanding of the control function from the extensive study of exact boundary controllability. Previous results obtained in the literatures are generalized.

：

[1] GUESMIA A. Exact controllability for wave equation with variable coefficients[J]. Israe Journa of Mathematicsm, 2001, 125: 83-92.

[2] A GUESMIA. On linear elasticity systems with variable coeffiecients [J]. Kyushu Journal of Mathematics, 1998, 52: 227-248.

[3] BARDOS C, LEBEAU G, R RAUCH. Sharp sucient conditions for the observation, control and stabilization of wave from the boundary [J]. SIAM J. Control Optim, 1992, 30: 1024-1065.

[4] E ZUAZUA. Exact controllability for the semilinear wave equation [J]. J. Math. Pures Appl. 1990, 69: 1-31.

[5] XU G. Q, YUNG S P, LI L K. Stabilization of wave systems with input delay in the boundary control [J].ESAIM Control Optim. Calc. Var, 2006, 12(4): 770-785.

[6] HAMCHI I. Uniform decay rates for second-order hyperbolic equations with variabl coefficients [J]. Asymptotic Analysis, 2008, 57: 71C82.

[7] WU J Q, LI S J. Stabilization of wave equation with variable coefficients by nonlinear boundary feedback [J]. J. Syst Sci Complex, 2011, 24: 875-882.

[8] LIONS J L. Exact controllability, stabilizability, and perturbation for distributed systems [J].SIAM Review, 1988, 30: 1-68.

[9] YU L. Exact boundary controllability for a kind of second order quasilinear hyperbolic systems and its applications, Math [J]. Methods Appl. Sci, 2010, 33(3): 263-272.

[10] M AASSILA. Exact boundary controllability of the plate equation [J]. Dierential Integrations, 2002, 13:1413-1428.

[11] M M CAVALCANTI, Exact controllability of the wave equation with mixed boundary condition and time-dependent coefficients [J]. Arch. Math. (Brno), 1999, 35: 29-57.

[12] GLOWINSKI R, LI C H, LIONS J L. A numerical approach to the exact boundary controllability of the wave equation (I). Dirichlet controls: Description of the numerical methods [J]. Japan J. Appl. Math, 1990, 7: 1-76.

[13] CHAI S, GUO Y, YAO P F. Boundary feedback stabilization of shallow shell [J]. SIAM J. Control Optim, 2004, 42(1): 239-259.

[14] CHAI S, LIU K. Observability inequalities for the transmission of shallow shells [J]. Systems Control Lett, 2006, 55: 726-735.

[15] LI T T. Exact boundary observability for 1-D quasilinear wave equations [J]. Math. Methods Appl. Sci, 2006, 29: 1543-1553.

[16] DUYCKAERTS T, ZHANG X, E ZUAZUA. On the optimality of the observability inequalities for parabolic and hyperbolic systems with potentials [J]. Ann. Inst.H. Poincar Anal. Non Linaire, 2008, 25: 1-41.

[17] LI T, RAO B P, WANG Z Q. A note on the one-side exact boundary observability for quasilinear hyperbolic systems [J]. Georgian Math. J, 2008, 15: 571-580.

[18] KOMORNIK V. Exact controllability and stabilization [D].Strasbourg Universite Louis Pasteur, 1993.

[19] LIU W. Stability and controllability for the transmission wave equation [J]. IEEE Trans. Automat. Control,2001, 46: 1900-1907.

[20] ZHOU Y, LEI Z. Local exact boundary controllability for nonlinear wave equations[J]. SIAM J. Control Optim. 2007, 46: 1022-1051.

[21] NING Z H, YAN Q X. Stabilization of the wave equation with variable coefficients and a delay in dissipative boundary feedback[J]. Math. Anal. Appl, 2010, 367: 167-173.

[22] ZHANG Z F, YAO P F. Global smooth solutions of the quasilinear wave equation with internal velocity feedbacks [J]. SIAM J. Control Optim, 2008, 47: 2044-2077.

[23] LIU Z, RAO B. A spectral approach to the indirect boundary control of a system of weakly coupled wave equations [J]. Discrete Contin. Dyn. Syst, 2009, 23: 399-414.