一种矩阵相乘的并行算法实现与性能评测

苑 野 ， 于永澔

(哈尔滨工业大学 基础与交叉科学研究院, 哈尔滨150080)

随着多核处理器技术、高速网络和分布式计算技术的发展，集群系统已经成为高性能计算领域最重要的计算平台[1].集群系统具有性能价格比高、可扩展性好、高可用性、高利用率和易用性好等特点.MPI(Message Passing Interface)[2]是面向并行编程环境下的一种基于消息传递的标准函数库，被广泛应用于分布式存储的可扩展的并行计算机(Scalable Parallel Computers)和工作站集群(Networks of Workstations).MPI具有较高的通信性能、程序可移植性好、可扩展性好、程序代码实现灵活及高效统一的编程环境等特点.由于集群系统具有典型的分布式存储特征， 因此MPI编程模型已经成为目前集群系统上主流的并行程序设计环境.

矩阵计算主要应用于科学与工程计算领域，是科学计算的核心问题.而矩阵相乘是矩阵计算最基本的运算.用传统的串行算法库进行矩阵相乘运算[3-4]会受到矩阵规模、单机硬件性能(CPU速度、内存大小、存储器空间)等方面的限制.对串行算法进行并行化处理，使其达到更高的运算性能，是解决上述限制的最有效途径.人们采用了各种方法对矩阵相乘进行并行化处理，并取得了一定的进展，主要包括基于顺序矩阵直接相乘算法(行列划分方法)、基于递归实现的块矩阵相乘方法、基于二维网格实现的矩阵相乘算法(Cannon算法、脉动阵列算法)和Strassen算法等.行列划分算法是经典的矩阵相乘算法中的一种，以其并行时间复杂性优良、代码简单且易于实现等优势使该方法备受研究者的重视.本文在集群环境下，使用SPMD计算模型及MPI消息传递技术对矩阵相乘的行列划分方法进行了并行化算法实现，并定量的对该并行算法的性能进行了测试，实验表明此并行算法在一定矩阵规模下具有较好的加速性能及效率，优于传统的串行算法.

1 MPI编程技术

MPI是一种消息传递编程模型[5]，并已经成为这种编程模型事实上的标准.它不是一种编程语言，而是一个并行函数库.MPI标准函数库为C语言和FORTRAN语言提供了通用的并行程序编程接口.一个MPI系统通常由一组函数库、头文件和相应的运行、调试环境组成.MPI并行程序通过调用MPI库中的函数来完成消息传递.

1.1 MPI基本概念

1.1.1 进程组(process group)

MPI程序全部进程集合的一个有序子集.进程组中的进程被赋予一个惟一的序号(rank)，用于标识该进程.

1.1.2 通信器(communicator)

由一个进程组和一个标识构成.在该进程组中，进程间可以相互通信.MPI程序中的所有通信必须在通信器中进行.默认的通信器是MPI_COMM_WORLD，所有启动的MPI进程通过调用函数MPI_Init()包含在通信器中，每个进程通过函数MPI_Comm_size()获取通信器中的初始MPI进程个数.通信器可分为在同一进程组内通信的域内通信器和在不同进程组进程间通信的域间通信器.

1.1.3 进程序号(rank)

MPI程序中用于标识进程组或通信器中一个进程的唯一编号，同一个进程在不同的进程组或通信器中可以有不同的序号.MPI_PROC_NULL代表空进程.

1.1.4 消息(message)

包括数据(data)和信封(envelope)两部分.数据包含用户将要传递的内容，信封由接收进程序号/发送进程序号、消息标号和通信器三部分组成.消息被封装在“信封”中，然后经缓冲区向网络传输层打包发送.

1.1.5 MPI对象

MPI系统内部定义的数据结构，包括数据类型、通信器(MPI_Comm)、通信请求(MPI_Request)等，它们对用户不透明.

1.1.6 MPI连接器(handles)

连接MPI对象的具体变量，用户可以通过它访问和参与相应的MPI对象的具体操作.

1.2 点对点通信

点对点通信是指在一对进程之间进行的消息收发操作，是MPI中最基本的通信模式.MPI提供阻塞型(blocking)和非阻塞型(non blocking)两种类型的点对点通信函数.阻塞型函数是指一个例程需等待操作完成才返回，返回后用户可以重新使用调用中所占用的资源.非阻塞型函数是指一个例程不必等待操作完成便可以返回，返回后用户不可重用所占用的资源.根据以上两类通信函数的不同特点，MPI提供了四种不同的通信模式，分别是标准模式(standard mode)、缓冲模式(buffered mode)、同步模式(synchronous mode)和就绪模式(ready mode).

1.3 聚合通信

聚合通信是指在一个通信器内的所有进程同时调用同一个聚合通信函数而进行的通信.聚合通信包括障碍同步(MPI_Barrier)、广播(MPI_Bcast)、数据收集(MPI_Gather)、数据发散(MPI_Scatter)、数据转置(MPI_Alltoall)和规约(MPI_Reduce).

2 矩阵乘法并行算法

集群上矩阵乘法并行算法采用了行列划分方法、SPMD计算模型和基于MPI消息传递的并行处理技术.假设A为m*k阶矩阵，B为k*n阶矩阵，C为m*n阶矩阵，计算问题C=A*B.令m=m`*p、n=n`*p，矩阵A=[A0tA1t…Ap-1t]，矩阵B=[B0B1…Bp-1]，矩阵A第i行的每个元素与矩阵B第j列的各元素分别相乘，并将乘积相加到矩阵C的第i行第j列的一个元素Ci,j，此时C=(Ci,j)=(AiBj).将j=0，1…，p-1存放在Pi中，使用p个处理机，每次每个处理机计算出一个Ci,j，需要p次完成.具体算法[6-7]如下：

begin

Mp1≡myid+1 mod p，mm1≡myid-1 mod p

for i=0 to p-1 do

l≡i+myid mod p

Cl=AB

If i≠p-1，send(B,mm1),recv(B,mp1)

endfor

endfor

在p=n2个处理器进行n*n矩阵乘法时，并行时间的复杂性为O(n).广播算法决定通信开销进而支配通信时间，n*n矩阵通过独立的消息分发到n2个从处理器上，每个从处理器向主处理器返回C的一个元素.其通信时间tcomm=n2(2tstartup+(2n+1)tdata)，其中tstartup是数据传送的延迟或启动时间，tdata是数据传输返回时间[8].

3 实验验证

本文的硬件测试环境是8个节点组成的集群系统，采用Infiniband高速网络互联，每个节点配有1颗Intel Xeon 2.5 G处理器，32 G内存，1 T SAS磁盘，GPFS共享文件系统，软件环境是Red Hat Linux操作系统，编译器为Intel C++ 13.0.1，MPI的版本为Intel MPI 4.1.

加速比和效率是衡量多处理机和单处理机系统相对性能的重要指标.把串行应用程序在单处理机上的执行时间和该程序并行化后在多处理机上的执行时间的比值定义为加速比，它是并行算法可扩展性的重要参数.将加速比与CPU个数之间的比值定义为效率，它反映了在某一时间段内，一个处理器真正用于计算的时间.设矩阵大小分别为1 200×1 200、4 000×4 000，8 000×8 000，各做5次实验，将5次计算时间的平均值作为执行时间.表1为单处理机系统的串行程序执行时间.表2为多处理机系统的并行程序执行时间.图1为矩阵并行程序运行时间变化.图2为不同矩阵规模下运行时间比较.

表1单处理机的串行执行时间

矩阵大小串行执行时间1 200×1 2000.411 1214 000×4 0001.124 6448 000×8 0003.280 423

表2多处理机并行程序执行时间

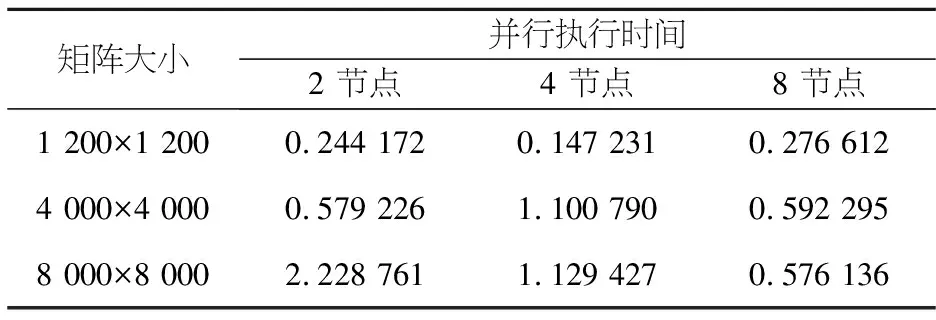
矩阵大小 并行执行时间 2 节点 4 节点 8 节点1 200×1 200 0.244 172 0.147 231 0.276 6124 000×4 000 0.579 226 1.100 790 0.592 2958 000×8 000 2.228 761 1.129 427 0.576 136

图1 矩阵并行程序运行时间

图2 不同矩阵规模下运行时间比较

如图1所示，可以看到在所有矩阵的多节点测试中，并行程序的运行时间随着矩阵规模不断变大时，其运行时间基本保持不断的增加.然而在节点较多(如node=8时)的并行环境下运行时，其并行程序运行时间随矩阵规模变化不明显.如在矩阵为4 000×4 000、8 000×8 000下，运行时间基本保持不变.这主要是因为在程序的执行时间中，绝大部分的时间用于数据的通信而非用于真正的计算.由图2可知，在矩阵规模很大时(当矩阵为8 000×8 000)，其运行时间随着节点数的增加而不断减少.其原因是用于计算的时间占了绝大部分，数据通信时间大量减少，并行计算的优势得到了体现.表3为多处理机并行算法的加速比和效率.图3为不同矩阵规模下加速比比较，图4为不同矩阵规模下并行效率比较.图5为矩阵规模在8 000阶下的加速比.

表3多处理机并行算法的加速比和效率

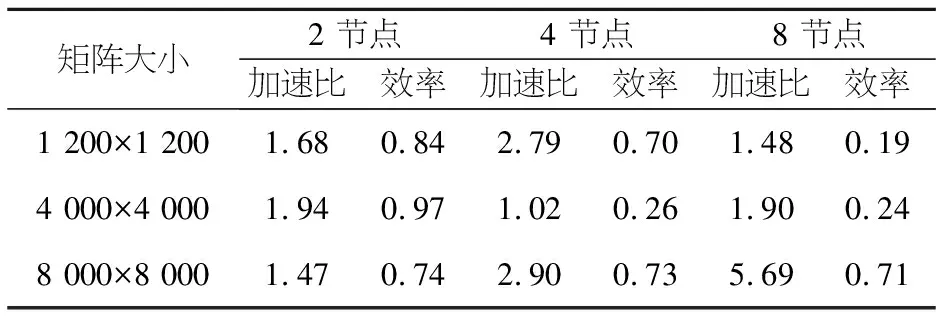
矩阵大小 2 节点 4 节点 8 节点加速比 效率加速比 效率加速比效率1 200×1 2001.680.842.790.701.480.194 000×4 0001.940.971.020.261.900.248 000×8 0001.470.742.900.735.690.71

图3 不同矩阵规模下加速比比较

图4 不同矩阵规模下并行效率比较

图5 矩阵规模在8 000阶下的加速比

如图3～5可知，该并行算法的在不同矩阵规模下，其加速比均大于1，这说明此算法与传统的串行算法相比具有较高的加速性能.当矩阵规模较小时(如矩阵为1 200×1 200时)，其加速比随着节点数的增加表现为先迅速变大，然后逐渐变小.并行效率呈现逐渐下降的趋势.在node=4时获得最大加速比2.79，此时的效率为70%.当矩阵的规模较大时(如矩阵为8 000×8 000)，其加速比几乎表现为线性增加，在node=8时获得最大加速比5.69，而并行效率几乎保持不变，基本维持的在72%左右.这说明此种并行算法在矩阵规模较大的条件下，加速效果明显，效率较高.

4 结 语

本文对集群计算环境下矩阵相乘问题应用SPMD计算模型和基于MPI消息传递技术实现了其并行算法，并通过实验验证了该算法的有效性.与传统的串行算法相比，结果证明此算法在一定的矩阵规模下具有较好的加速性能及效率.

参考文献：

[1] CHAI L, LAI P, JIN H,etal. Designing an efficient kernel-level and user-level hybrid approach for mpi intra-node communication on muti-core systems[C]//ICPP’08:Proceedings of the 2008 37th International Conference on Parallel Processing，Washington DC: IEEE Computer Society, 2008.

[2] MPI: A Message-Passing Interface Standard[S].

[3] BLACKFORD L S, DEMMEL J, J DONGARRA,etal. An update set of basic linear algebra subprograms(BLAS)[J]. ACM Transactions on Mathematical Software，2002, 28(2): 135-151.

[4] COHN H, KLEINBERG R, SZEGEDY B,etal. Group-theoretic algorithms for matrix multiplication[C]//Proceedings of the 46th Annual Symposium on Foundations of Computer Science, 23-25 ，2005.

[5] MCQUILLAN J M, D WALDEN C. Some considerations for a high performance message-based interprocess communication system [J]. SIGOPS Oper.Syst.Rev., 1975, 9: 77-86.

[6] 张林波, 迟学斌. 并行算法导论[M]. 北京: 清华大学出版社，2006.

[7] 陆鑫达. 并行程序设计[M]. 北京: 机械工业出版社, 2006.

[8] 徐红波，胡 文，潘海为，等.高维空间范围查询并行算法研究[J].哈尔滨商业大学学报：自然科学版，2013，29(1)：73-75，111.