关于滴状冷凝成核密度和热交换系数的研究
梅茂飞, 胡 峰, 韩 崇
(徐州工程学院 数学与物理科学学院,江苏 徐州 221111)
0 引言
自Schmidt等[1]发现滴状冷凝这种更为高效的相变传热方式之后,众多学者就滴状冷凝中的热质传递现象进行了大量研究.其中,我国学者开展了许多重要的、开创性的工作[2-5].
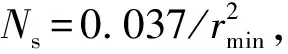
(1)
这里ΔT为气体与凝结表面之间的温差,Ts为饱和蒸汽温度,Hfg为汽化潜热,σ和ρ分别为液滴的表面张力和密度.从方程(1)可以看出,对于相同的凝结工质和饱和蒸汽温度,成核密度只与温差有关,而与固体表面的几何形貌无关.而Mu等[7]通过观察镁表面氧元素的增加量,发现成核密度与镁表面的粗糙程度成正比.综合Rose和Mu等的观点,冷凝表面的成核密度应该既与温差有关,又与表面的粗糙形貌有关.由于缺少测定成核密度的有效实验手段,目前研究成核密度对滴状冷凝热交换的影响主要依靠数值模拟[8]和理论分析[9].本文将通过数值模拟研究冷凝表面的液滴生长过程.
1 粗糙表面成核密度
令面积为Af的粗糙表面液滴成核密度为Nf,粗糙表面在光滑表面的投影面积为A0,投影表面上液滴成核密度为N0.若粗糙表面与光滑表面的成核密度成正比,则有
(2)
这里f=Af/A0表示实际面积与其投影面积之比,称为粗糙因子.从方程(2)可知,若光滑表面的成核密度为1010cm-2,f=2的粗糙表面可以使Nf增加一倍.由于最小液滴尺寸为纳米量级,纳米结构的粗糙表面对液滴的成核密度影响较小,本文的粗糙表面主要指具有微米结构的表面.在光滑表面,若初始液滴呈正方形排列,液滴之间的平均等效间隔记为de,于是,N0=A0/(de+2rmin)2,令de/rmin=a,则
(3)
将方程(3)带入(2)可得
(4)
由于成核液滴的最小半径可由方程(1)表示,所以
(5)
其中a表示光滑表面凝结核的疏密程度,称为密集度.对于相同的温差,a越小意味着液滴的密集程度越高,说明表面的成核密度也越大;a=0意味着相邻两个液滴相切.(5)式说明成核密度不但受温差,而且受粗糙因子的影响.对于1 cm2的区域,以水蒸气为凝结工质,图1为方程(5)的预测值与实验数据[10]的比较.图中的实验数据是利用Getdate软件从文献[10]中截取,并利用1stOpt软件将方程(5)和文献[10]的实验数据进行拟合,得出f和a的最佳估算值分别约为2和6 500.由于文献[10]中初始液滴的分布非常稀疏,所以密集度a较大.
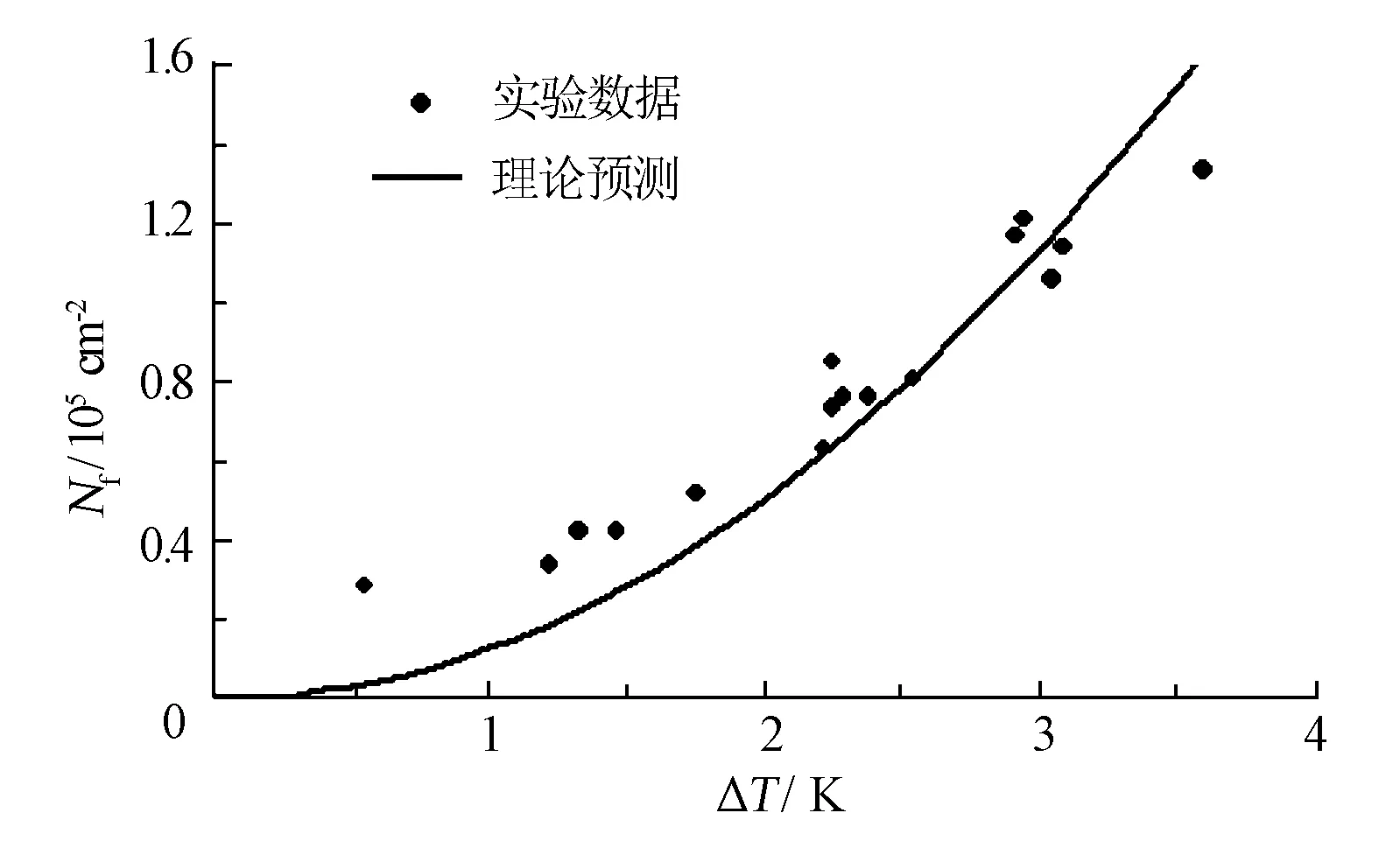
图1 凝结表面液滴成核密度的理论预测和实验数据比较
从图1可以看出,理论预测值与实验值在ΔT>2 K时吻合得较好.当ΔT→0时,凝结表面几乎没有初始液滴生成,而在实际的滴状冷凝过程中,因温度场和浓度场的脉动,仍会有初始液滴形成,故此时预测值与实验值出现明显差异.
2 滴状冷凝的数值模拟
2.1 模拟区域的选择
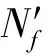

表1 不同温差下凝结表面的成核密度和最小液滴半径
2.2 数值模拟过程的描述
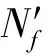
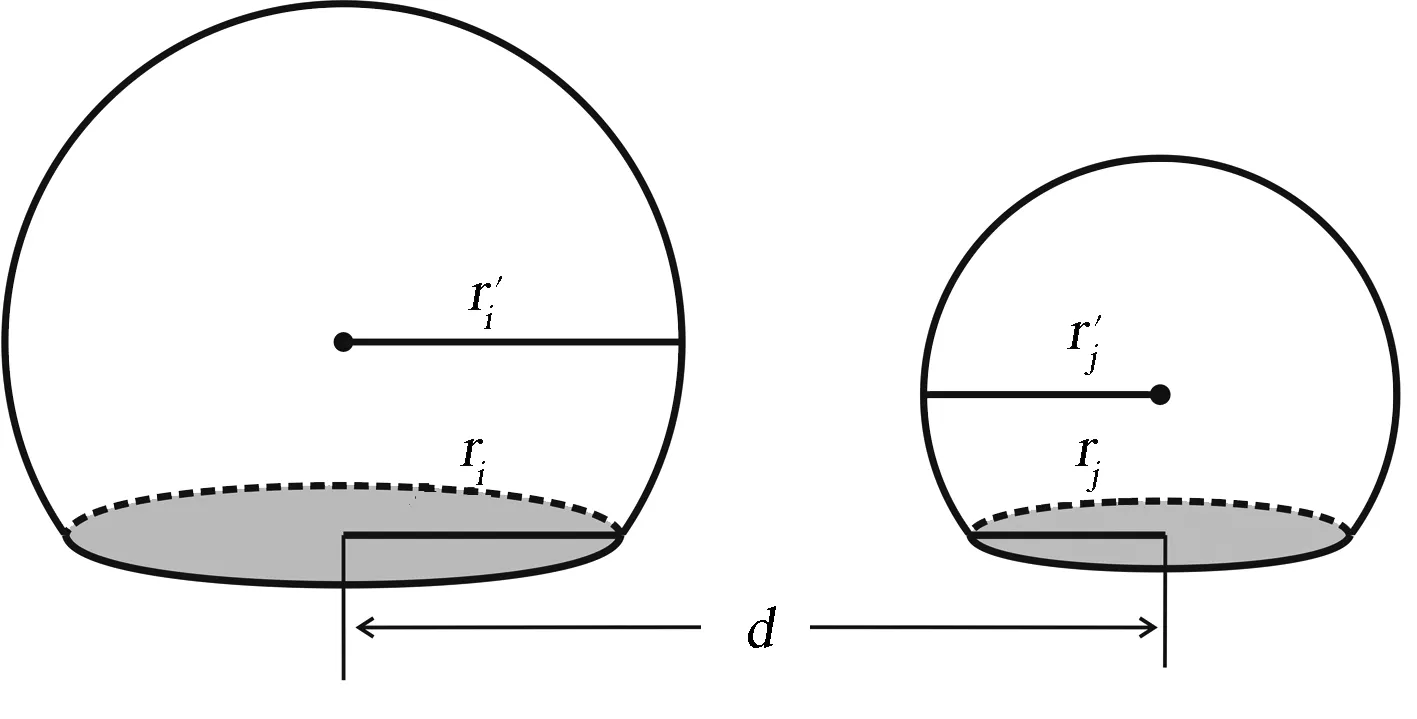
图2 邻近两个球形液滴的间隔
由于大液滴的表面面积较大,其表面张力和基底的粘附阻力比小液滴更大,因此,新液滴的重心靠近大液滴.为了简便起见,规定合并后液滴的重心与大液滴的重心重合[13].当表面对最大液滴的粘附力小于其重力时,最大液滴就会从凝结表面滑落,并且扫除沿途所接触的所有液滴,留下一道裸露的冷凝表面.接着,水蒸气又会在裸露表面重新凝结生长.在模拟液滴脱落时,脱落行为是瞬间的.
3 结果与讨论
首先,考察液滴尺寸分布函数N.Δr·N表示半径落在r-Δr到r+Δr之间的液滴数目,一般地,Δr=0.2r[14].Mei等[12]将凝结表面的液滴类比成多孔介质中的孔隙[15],应用分形几何理论和方法,给出了液滴尺寸分布的微分形式
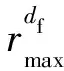
(6)
这里df是液滴尺寸分布的分形维数,rmax是液滴的最大半径.从方程(6)即可获得液滴尺寸分布函数
(7)
在数值模拟中,每迭代一次,就计算出Δri内的液滴数目Δri·Ni,再利用最小二乘法对数据进行拟合.拟合结果显示,logN(r)与logr之间存在线性关系,其斜率为(-df-1).模拟结果得出,最大液滴第一次脱落事件大约发生在第300次迭代.为了考察液滴脱落和重新凝结对液滴尺寸分布的影响,总的迭代次数设定为1 000.图3(a)~(e)显示不同温差下液滴尺寸分布分形维数随迭代次数的变化情况.由于大液滴不断从凝结表面滑落带走所接触的液滴,在液滴滑过的裸露区域又会有大量的初始液滴出现,所以,分形维数会围绕着某个平均值上下波动.图3(f)给出了分形维数的平均值与温差的变化关系,可以发现,分形维数增加的趋势随着温差的增大逐渐减缓.这是因为,随着温差的增大,由于滑落被带走的液滴数目占整个表面液滴的比例降低,从而对液滴尺寸分布的影响减弱.
其次,考察温差对表面热交换系数的影响.对于接触角为90°的单个液滴的热流可以表述为[7,10]
(8)
其中q,k分别为热流量和液体的热导率;hi为气液界面的热交换系数,对于温度为373 K和304 K的气体,分别取1.5×107,1.5×106W/(m2K)[8].
根据方程(8),凝结表面的热交换系数为
(9)
这里qi,si分别是第i个液滴的热流和底面积;n表示凝结表面总的液滴数目.图4显示表面热交换系数随液滴尺寸的变化.从图中可以发现,液滴存在一个最佳尺寸,使得热交换系数达到最大,并且最佳尺寸随着温差的增大而减小.当液滴尺寸达到微米量级时,不同温差下,液滴的热交换系数近乎相等,这主要是因为液滴尺寸达到微米量级以后,液滴自身的热阻对传热起着决定性的作用.
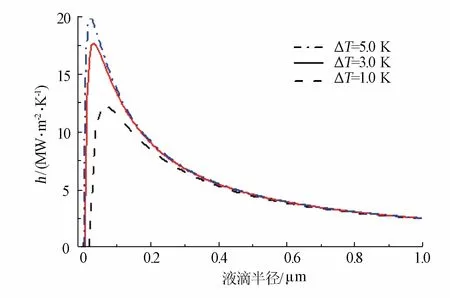
图4 单个液滴的热交换系数随液滴尺寸的变化
图5(a)~(e)显示了不同温差条件下凝结表面热交换系数随迭代次数的变化.可以发现,经过几十次迭代后,表面热交换系数达到最大,这是因为液滴的尺寸达到了最佳尺寸(图4).接着表面热交换系数出现波动情况,而且,温差越大,这种波动情况越密集.这是由于温差的增大,在裸露表面有更多的初始液滴生长.由图4可知,表面热交换系数的主要贡献来自于小液滴,所以,在温差大的表面,液滴滑落会造成表面热交换系数更强烈的波动.图5(f)显示平均热交换系数随温差的增加而增大,这与现有的实验测量是一致的[16].因此,在已知冷凝表面的粗糙度和凝结核密度的情况下,本文的模拟方法可预测冷凝表面热交换系数随温差的变化.
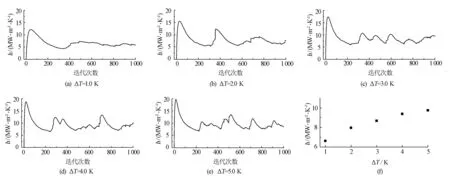
图5 凝结表面热交换系数随迭代次数及温差的变化
4 结论
根据液滴成核密度表达式,利用计算机模拟了温差从1 K变化到5 K的凝结表面液滴成核、生长、滑落和重新凝结的过程.结果显示,液滴尺寸分布分形维数和冷凝表面的热交换系数随着温差增大而增大.该方法作为实验研究的有效辅助手段,可减少试验次数,预测具有最佳热交换性能的冷凝表面.
感谢郁伯铭教授对本文提出的宝贵意见.
参考文献:
[1] Schmidt E,Schurig W,Sellschopp W.Versuche über die kondensation in film-und tropfenform[J].Tech Mech Thermodynamik,1930(1):53.
[2] 程延海,朱真才,韩正铜,等.镀层换热表面凝结传热实验研究[J].中国电机工程学报,2010,30(8):27.
[3] 兰忠,马学虎,王爱丽,等.低压蒸汽滴状冷凝过程中液滴生长特性[J].工程热物理学报,2012,33(1):139.
[4] Liu Tianqing,Sun Wei,Sun Xiangyu,et al.Thermodynamic analysis of the effect of the hierarchical architecture of a superhydrophobic surface on a condensed drop state[J].Langmuir,2010,26(18):14835.
[5] 程延海,朱真才,张世举,等.热交换器表面镀层对传热性能的影响[J].工程热物理学报,2012,33(1):128.
[6] Rose J W.Further aspects of dropwise condensation theory[J].Int J Heat Mass Transfer,1965,19:1363.
[7] Mu Chunfeng,Pang Jingjing,Lu Qiaoyu,et al.Effects of surface topography of material on nucleation site density of dropwise condensation[J].Chem Engin Sci,2008,63(4):874.
[8] Glickman L R,Andrew W,Hunt J R.Numerical simulation of dropwise condensation[J].Int J Heat Mass Tran,1972,15(11):2251.
[9] Wu Wenhai,Maa J R.On the heat transfer in dropwise condensation[J].Chem Engin J,1976,12:225.
[10] McCormick J L,Westwater J W.Drop dynamics and heat transfer during dropwise condensation of water vapour on a horizontal surface[J].Chem Engng Prog Symp Ser,1966,64:120.
[11] 杨春信,王立刚,袁修干,等.珠状凝结是一种典型的分形生长[J].航空动力学报,1998,13(3):271.
[12] Mei Maofei,Yu Boming,Cai Jianchao,et al.A fractal analysis of dropwise condensation heat transfer[J].Int J Heat Mass Tran,2009,52(21/22):4823.
[13] Rose J W,Glicksman L R.Dropwise condensation—the distributions of drop size[J].Int J Heat Mass Tran,1973,16(2):411.
[14] Ichiro Tanasawa,Ochiaiand Jun-ichi.Experimental study on dropwise condensation[J].Bulletin of the JSME,1973,16(1):1184.
[15] Yu Boming,Cheng Ping.Fractal models for the effective thermal conductivity of bidispersed porous media[J].AIAA J Thermophys Heat Transfer,2002,16:2229.
[16] Rose J W.Dropwise condensation theory and experiment:a review[C]//Proc Instit Mechan Engin,2002,216:115-127.

