基于海明距离改进的自适应遗传算法

巩 固， 郝国生， 王文虎

(1.江苏师范大学 计算机科学与技术学院,江苏 徐州 221116; 2.江苏师范大学 科文学院,江苏 徐州 221116)

0 引言

遗传算法(genetic algorithm,GA)是模拟生物进化论的仿生算法,具有简单、通用、鲁棒性强和适于并行分布处理的特点．自1975年Holland系统提出遗传算法以来,很多研究者一直致力于推动遗传算法的改进和发展,在编码方式、控制参数的确定、预防陷于局部最优等方面进行了深入的研究,提出了各种改进的遗传算法．Srinivas等[1]1994年提出了一种自适应遗传算法(adaptive general algorithm,AGA),实现交叉概率Pc和变异概率Pm随群体的适应度自动改变[1-3]．算法运行中,当种群个体的适应度趋于一致或者局部最优时,Pc和Pm增加,以跳出局部最优;当群体个体适应度比较分散时,Pc和Pm减少,以利于优良个体的生存[4-6]．

虽然遗传算法得到了极大的发展和应用,但仍存在着局部搜索能力不够、欺骗问题和“早熟”现象等[3-5]，影响了算法的全局收敛性和计算性能[2,6-7]．很多研究者针对“早熟”现象提出了不同解决方法,如分层遗传算法、CHC算法、messy GA、基于小生境技术的遗传算法、并行遗传算法等,但是“早熟”现象仍然存在,在具体应用中影响到结果的正确获取[8-10]．针对AGA算法的不足,本文提出基因间距思想,利用Hamming距离控制种群的个体差异,将优良基因很好地遗传到下一代,使得染色体可以到达的范围更大,从而产生最优解的机会就变大．在这些工作的基础上，给出了仿真实验,结果验证了改进的自适应遗传算法的有效性，且该算法增强了全局收敛性．

1 自适应遗传算法与改进

1.1 自适应遗传算法

遗传算法参数中的Pc和Pm对算法的性能起着非常重要的作用．若采用固定的Pc和Pm值难以适应种群状态的变化,有时候导致进化过程停滞不前．Srinvivas等提出一种自适应遗传算法,该算法中Pc和Pm能随适应值自动改变[1]．同时,适应值高于群体平均适应值的个体,对应于较低的Pc和Pm,使得上代较优解基因能进入下一代;而低于平均适应值的个体,对应于较高的Pc和Pm,对应解被淘汰掉.所以AGA的Pc和Pm能提供相对某个解的最佳Pc和Pm．AGA在保持群体多样性的同时,保证了遗传算法的收敛性．Srinvivas等提出的自适应算法中Pc和Pm公式[1-2,5]如下：

式中fmax为群体中最大的适应度值,favg为每代群体的平均适应度值,f′为要交叉的两个个体中较大的适应度值,f为要变异个体的适应度值,k1,k2,k3和k4为(0,1)之间的值．

由于Pc和Pm对遗传算法的性能影响较大,故应防止因Pc和Pm选择不当造成算法过早收敛或收敛速度慢的现象出现．但Pc和Pm的选取不能简单地随适应度线性变化．本文结合文献[4-7]的思想,采用余弦形式改进自适应遗传算法算子,构造的自适应遗传算子为

1.2 自适应遗传算法的改进

用Hamming距离控制初始种群的个体差异,以扩大种群的多样性,遏制超长个体的快速繁殖．方法如下:在产生初始种群的过程中,每产生一个新个体都与前面的所有个体进行比较,若新个体与前面某一个个体的Hamming距离小于某一设定值(一般为3到5,该数的设定与链码长度有关),则停止比较，跳出循环,重新产生新个体,直到得到所有个体间均有一定差异的种群．由于种群中的个体解遍及整个解空间,因而能很好地反映搜索空间,从而扩大种群的多样性,遏制超长个体的快速繁殖．依据Hamming距离Hij产生初始种群,使得初始种群的各个体之间保持一定的距离,各个体尽可能均匀地分布在整个解空间上．

两个个体基因组字符串中字符不相同的数目为两个基因组字符串的Hamming距离,距离越大,则两个个体基因组字符串间所包含的不相同模式的数量就越多,种群中的模式也就越多,两个个体所对应的参数差别也越大．考虑到形成初始种群时的方便、快速以及尽可能均匀分布,初始种群的任何两个个体之间要满足如下条件:

在进行选择操作时,采用竞争选择并采用最优保留策略．由于两个相近个体的杂交很难产生相对较好的个体,因此要对被选择的两个个体进行海明距离判断,以增加杂交后代的多样性,产生更好的个体,促进杂交后代的改良．被选择的两个个体的海明距离要满足如下要求：

Hij≥0.33Nch,

式中Nch为基因组字符串的长度．个体基因串满足要求,则被选择；否则重新进行选择.这样就增加了两个被选择个体杂交后产生优良后代的概率．

当种群进化到一定程度时,个体之间的相似度随进化代数逐渐提高,如果仅用Hamming距离来判断个体之间的相似性,则有可能碰到“海明悬崖”问题,即Hamming距离较近的个体其欧式距离有可能比较远,两者的变化不一致．如A，B两个个体基因如下：

同为30位长度的二进制基因串,个体基因串均采用一个20位长二进制基因串(个体基因组串左边)和一个10位基因串(个体基因组串右边)自变量构成．两个个体的模式看似存在很大的相似性,仅在第9位和第25位(由右边计算位置,第一个为0)上存在差异,但其表现型在实际地理位置上却相距很远．为了避开海明悬崖问题,文中对于基因型个体之间的相似性问题,引入基因座权重

式中i表示第i位基因座.根据基因座权重的定义,个体如果在第i位基因值存在差异,且i越大,则个体表现型之间的距离越远．

在AGA中,因早期出现的优良个体被过分保护,使得算法将迅速向最优解收敛,而在算法中后期,种群中的个体因过于集中又会使交叉操作丧失产生新模式的能力,同时因大部分个体适应度都接近种群平均适应度,变异概率较小又使得算法很快就收敛到局部最优解．本文的算法中,以配对个体的差异度作为设置交叉概率的出发点,差异度越大说明它们通过交叉操作相互交换信息的价值也越大,而且以差异度来衡量交叉率也可以避免近亲之间的交叉繁殖．以单点交叉操作为例,假设个体基因长度是L,而配对的2个个体不同的基因位数是m位(即它们的海明距离是m)，则任选交叉点而将这m个基因分在交叉点同侧的可能情形共有N种：

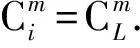
适应度函数

θ=Jf(x)+Wif(x),

式中f(x)为目标优化函数，

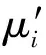
在代数迭代过程中,为了很好地检查局部个体基因串演变情况,每隔3代按

%

检查运算一次．当所有种群的基因串与最优个体的海明距离与个体基因串的比值小于5%时,则进行种群中的最优个体保留策略,其他个体随机产生.这样可以避免在AGA运行的中后期,因种群中的个体过于集中，使交叉操作丧失产生新模式的能力;同时,因大部分个体适应度都接近种群平均适应度,变异概率较小又使得算法很快就收敛到局部最优解问题．

对于文中优化的自适应遗传算法的终止条件,采用按两代种群中最大适应度的相对误差来确定.算法终止评判标准为

<ε,

式中E(Gk+1,Gk)表示两次迭代的误差,maxGk+1和maxGk分别表示第k次和k+1次迭代时个体基因串的最大适应度值的倒数,ε为算法给定的评判标准．当然，算法如果运行500代以上也可终止,采用该终止条件主要是由于遗传算法具有较大的随机性．

2 实验结果与分析

为验证本文提出算法的有效性,采用几组多峰值函数获取最优解实例,利用Matlab 7.0编程和舍费尔德(Sheffield)大学开发的遗传算法工具箱[11],遗传算法参考文献[2-3]的附录源程序,分别对标准遗传算法(SGA)、未改进的自适应遗传算法和改进的自适应遗传算法(IAGA)最优解寻找过程进行比较．个体编码采用二进制编码．3个函数如下：

-100≤x,y≤100;

maxf2=xsin(10πx)+2.0, -1≤x≤2;

-5.12≤x,y≤5.12.

实验对每个函数运行最大次数为50次,种群采用最大100,编码采用32位．实验对比结果见表1．

3个函数有多个局部极值点,SGA很容易陷入早熟,停滞在局部极值点．f1函数只有一个(0,0)为全局最大点,最大值周围有一个圈脊,取值均为0.990 283,函数采用SGA很容易陷入此局部极值点而出现早熟现象．函数f2有多个极值点,SGA也容易出现早熟现象．函数f3是大海捞针类求解最优化,是一个典型的遗传算法欺骗问题,当x=0,y=0时，函数有最大值3 600．函数有4个局部极值点,分别为(-5.12,5.12),(-5.12,-5.12),(5.12,5.12)和(5.12,-5.12),函数均值为2 748.78．

由表1的实验结果和图1可以看出,与标准遗传算法和自适应遗传算法相比,改进的自适应遗传算法所求得的函数平均值更接近于函数的最优值,平均进化代数也明显较少且搜索成功率较高．因此,提出的自适应遗传算法不仅能得到更优的函数最优解,而且收敛速度和搜索成功率也得到提高．

表1 函数优化研究结果

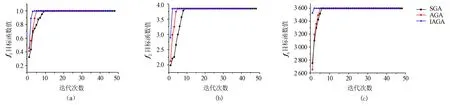
图1 函数f1(a),f2(b),f3(c)最优解的变化

3 结束语

为了解决遗传算法种群出现早熟和容易陷入局部最优的问题,本文在AGA和基因海明距离计算的基础上，提出了对自适应遗传算法的改进策略,并用实例验证了本文提出的算法在一些性能上要优于GA和AGA,较好地避免了GA的早熟出现，也提高了AGA的效率.仿真实验结果显示，改进的遗传算法能较好维持种群的多样性,并能有效地提高全局搜索能力和局部快速搜索能力．

参考文献:

[1] Srinivas M,Patnaik L M.Adaptive probabilities of crossover and mutation in genetic algorithm[J].IEEE Trans on Systems,Man & Cybernetics,1994,24(2):656.

[2] 王小平,曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2003.

[3] 韩瑞锋.遗传算法原理与应用实例[M].北京:兵器工业出版社,2009.

[4] 林明玉,黎明,周琳霞.基于可进化性的自适应遗传算法[J].计算机工程,2010,36(20):1735.

[5] 沈斌,周莹君,王家海.基于自适应遗传算法的流水车间作业调度[J].计算机工程,2010,36(14):201.

[6] Hwang S F,He R S.Improving real-parameter genetic algorithm with simulated annealing for engineering problem[J].Advances Engineering Software,2006,37(6):406.

[7] Zhang J,Chung H S H,Lo W L.Clustering—based adaptive crossover and mutation probabilities for genetic algorithms[J].IEEE Transactions on Evolutionary Computation,2006,11(1):326.

[8] Dilettoso E,Salerno N.A self-adaptive nicking genetic algorithm for multimodal optimization of electromagnetic devices[J].IEEE Transactions on Magnetics,2006,42(2):1203.

[9] Wang Hongjian,Zhao Jie,Bian Xinqian,et al.An improved path planner based on adaptive genetic algorithm for autonomous underwater vehicle[C]//Proceedings of the IEEE International Conference on Mechatronics and Automation,2005，2:857.

[10] 黄永清,梁昌勇,张祥德,等.一种小种群自适应遗传算法[J].系统工程理论与实践,2005,25(11):92.

[11] 雷英杰,张善文.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.