基于自适应进化神经网络算法的入侵检测*

杨宏宇,赵明瑞,谢丽霞

(中国民航大学计算机科学与技术学院,天津 300300)

基于自适应进化神经网络算法的入侵检测*

杨宏宇,赵明瑞,谢丽霞

(中国民航大学计算机科学与技术学院,天津 300300)

针对目前多数入侵检测系统的低检测率问题，提出一种自适应进化神经网络算法AENNA。基于遗传算法和BP神经网络算法，利用模拟退火算法的概率突跳和局部搜索强的特性对遗传算法进行改进，采用双种群策略的遗传进化规则实现BP神经网络权值和结构的双重优化；通过对遗传算法的交叉算子与变异算子的改进，设计一种自适应的神经网络训练方法。实验结果表明，基于AENNA的入侵检测方法能够有效提高系统的检测率并降低误报率。

遗传算法；神经网络算法；模拟退火算法；入侵检测

1 引言

当今社会，随着网络技术和网络规模的不断发展，针对网络和计算机系统的攻击变得越来越频繁，攻击手法也复杂多样。而传统的入侵检测技术由于技术自身的局限和不足已无法满足安全高度敏感部门的需求，研究人员对诸如神经网络技术、专家系统、机器学习和进化算法等智能方法在入侵检测中的应用开展了大量研究，为入侵检测领域的研究开启了一个崭新的方向[1]。

文献[2]在基于最小闭包球的支持向量机算法的基础上，提出了基于广泛内核的最小闭包球算法的入侵检测方法,但该方法无法高效处理多类问题且范围限制严格。文献[3]提出一种基于关联决策的网络多源入侵检测算法，该算法运用模糊识别手段，通过计算各个多源子攻击的关联度，对入侵行为进行模糊差异聚类，完成入侵检测，但过于依赖参数特征的计算准确性，对预分类的结果影响较大。文献[4]提出一种神经网络专家系统模型，并将该模型应用于入侵检测系统，通过关联检测性能的方法扩充了单一系统的检测能力，但该模型也增加了检测时间，时间复杂度偏高。文献[5]提出一种自适应遗传算法，该算法首先考虑个体适应度的变化，并将交叉和变异概率在最大适应度与平均适应度之间作线性变换，但该算法在演化初期，较优个体几乎不发生变化，因此容易走向局部收敛。文献[6]提出一种改进的自适应遗传算法，并有效地应用到非线性系统的参数辨识问题上，但该算法中的局部较优个体不易被淘汰，全局搜索能力不强，且对于分布偏多于平均适应度范围的种群演化容易停滞不前。

传统神经网络算法的收敛速度较慢；遗传算法局部搜索能力差但全局搜索能力却很强；模拟退火算法具有强收敛及概率突跳的特性。本文基于智能互补融合的观点，将遗传算法、模拟退火算法和神经网络结合提出一种自适应进化神经网络算法AENNA(Adaptive Evolutionary Neural Network Algorithm)。

2 神经网络改进进化算法

2.1 改进算法设计思路

传统BP算法虽然具有简单和可塑的优点，但由于BP算法本质上是采用梯度下降搜索方法，因而不可避免地存在固有的不足，如易陷入误差函数的局部极小点，而且对于较大搜索空间、多峰值和不可微函数等问题也不能有效搜索到全局极小点。而遗传算法是克服这一不足的有效解决办法，主要是由于遗传算法是一种全局优化搜索算法，因而能够避开局部极小点，而且在进化过程中无需提供所要解决问题的梯度信息。另一方面，标准遗传算法易出现未成熟收敛现象，虽然相应的改进方法很多，如调整操作参数、增加种群规模等，但都没有考虑使改进后的算法具有学习能力和鲁棒特性，这恰是神经网络的优势所在。因此，本文提出一种自适应进化神经网络算法 (AENNA)，通过改进遗传算法，优化BP神经网络的连接权值与网络结构，应用于BP神经网络的训练。

鉴于传统遗传算法个体的多样性下降过快，影响遗传算法通过交叉和变异跳出局部最优的能力，本文采用双种群遗传策略。此策略属于并行遗传策略，即同时进行多种群的进化，这种策略的优点在于可以改变种群内停滞的局面，在交换不同种群中优秀个体遗传信息的同时，能够跳出局部最优，这也加快了算法的进化速度。

用一个类来表示群体中的每个个体，同一种群的不同个体具有不同的隐含层数、节点数和连接权值。大种群中每个个体都来自一个小种群，小种群中所有个体均具有相同的网络结构、不同的连接权值。不同小种群中的个体在群体内进化，小种群中适应度较高的个体则有较大概率进入大种群进行交叉和变异操作，而后回到原小种群进行下一次的小群体内部进化。小种群中的进化操作选用调整的自适应交叉算子和变异算子，大种群中的进化操作则采用调整的增加算子和删除算子。

考虑到模拟退火算法在解决大型优化组合问题上的有效性，本文将其引入到对遗传算法的改进中，结合遗传算法群体并行搜索能力和模拟退火概率突跳特性来改善优化效率并避免局部极小的可能性。

遗传算法中交叉算子和变异算子对于遗传算法解空间的影响较大，这是由于交叉算子会造成染色体局部相似，交叉概率偏大会破坏适应度值高的个体，偏小则容易让算法停滞；同样，变异概率过大则变成了纯粹的随机搜索，过小则会导致无法驱动搜索转向其他解空间，而无法接近最优解。在参考了文献[5,6]提出的自适应遗传算法的基础上，本文从小种群的交叉算子和小种群变异算子两方面对遗传算法进行改进。

2.2 小种群交叉算子

小种群选用调整自适应交叉算子进行种群个体间的交叉。根据种群适应度值的大小，逐渐地调整整个种群的交叉概率。调整后的交叉概率Pc的计算公式[6]为：

(1)

其中,fa表示最大适应度值，fi表示最小适应度值，fv表示平均适应度值，这三个值用来表示种群适应度的集中程度，使Pc随适应度值在fa、fi和fv之间进行变化。f′为待交叉的两个个体中较大的适应度值。公式中k1=0.6，k3=0.9，k2在(k1,k3)间取值。适应度函数为：

(2)

其中，F为适应度函数值，取值在[0,1]之间；E为误差函数值；N为训练样本总数；ok(t)表示期望输出；yk(t)表示网络的实际输出[7]。

对于个体的选择，采用高适应度值、高概率中选方法将个体从父代中选出，其中概率pi的计算公式[8]为：

(3)

(4)

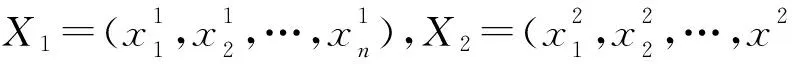
(5)

(6)

由于模拟退火法能有效解决大规模的组合优化问题，所以运用模拟退火机制[10]对交叉后生成的子代进行取舍，具体步骤设计为：

步骤1依据式(5)和式(6)对父代个体X1、X2进行交叉，生成子代个体Y1、Y2，按照式(2)计算子代个体的适应度值F(Y1)、F(Y2)。

步骤2若F(Y1)>F(X1)且F(Y2)>F(X2)，则子代个体Y1取代父代个体X1，子代个体Y2取代父代个体X2，转向步骤4；否则，若子代个体的适应度值小于父代个体的适应度值,则进行步骤3操作。

步骤3在[0,1]产生随机数β，计算Δ=F(X)-F(Y)，其中，X为父代的个体，Y为子代个体；

其中，T0为初始温度，d为初始种群个体间适应度的最大差值，α取0.01；Ti=T0(0.99i-1)，其中，i为进化代数；

Prob=min(1.0,exp(-Δ/Ti))

若Prob≥β，则子代个体Y取代父代个体X;否则保留父代个体X。

步骤4输出取舍后的个体。

2.3 小种群变异算子

小种群采用调整自适应变异算子进行个体变异操作。变异概率依据适应度值的集中程度自适应地变化，通过设置参数区间来限制变异概率的取值范围，可有效保证变异操作的合理性，调整后的变异概率Pm计算公式[9]为：

(7)

其中，fa、fv和fi分别代表种群中的最大适应度值、平均适应度值和最小适应度值；f为待变异的个体适应度值；k1=0.1，k3=0.09，k2均在(k3,k1)取值。

(8)

其中，t表示种群的总进化代数，r表示在[0,1]内非均匀分布的随机数，T表示最大的进化代数，b表示系统参数(通常设为2)。

3 算法流程设计

在对神经网络进化算法的改进中，在交叉概率算子和变异概率算子的计算中采用了个体适应度概率方差，这样能提高遗传算法的收敛速度。同时，引入模拟退火算法对交叉子代进行取舍，也加快了遗传迭代的进度。基于前文对神经网络进化算法的改进并参考文献[11]，设计AENNA的实现步骤如下：

步骤1设定初始参数。设置BP神经网络的层数、每层神经元个数、样本数据模式和误差值等。

步骤2初始化操作。用符合正态分布的小随机数随机产生p个染色体bi作为初始化的大种群。

步骤3估算操作。根据权值、阈值向量，用BP算法处理输入、输出样本，获得全局误差E。若E满足条件，则结束，若个体适应度值符合设定要求，则结束；否则转入步骤4。

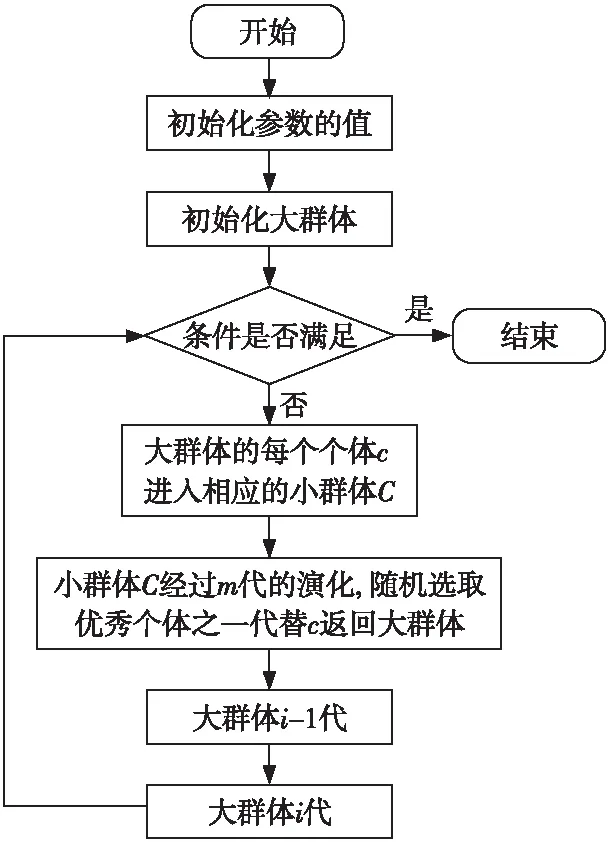
步骤4小种群演化操作(小种群的演化操作流程如图1所示)。将大种群中的个体按照编码长度的差异重组为多个小种群，并对每个小种群进行m代的进化处理。

步骤4.1选择操作。按式(3)和式(4)的选取概率，采用高适应度值、高概率选择法从父代中选择个体进行计算。

步骤4.2交叉操作。按式(1)计算交叉概率，并依据式(5)和式(6)进行交叉运算。

步骤4.3对交叉后的个体进行模拟退火处理，做出必要的取舍。

步骤4.4变异操作。按式(7)计算变异概率，并依据式(8)进行变异运算。

步骤4.5判断操作。若进化代数G

Figure 1 Small population evolution process图1 小种群演化操作流程

步骤5大种群演化(大种群演化操作流程如图2所示)。大种群中主要是不同结构网络的演化竞争，个体按式(3)和式(4)的选择概率计算公式进行改变其网络结构的演化运算，其变异算子步骤如下：

步骤5.1删除操作。将隐含层中所包含的某些节点的权值设置为0，即删除节点及其连接。

步骤5.2增加操作。添加一些节点到隐含层，并产生相应的权值，然后按式(7)进行自适应变异。

步骤6新的大种群重组，转到步骤3。

Figure 2 Big population evolution process图2 大种群演化操作流程

4 基于AENNA的入侵检测

基于AENNA算法的入侵检测系统模型如图3所示，其中包括数据捕获引擎、特征提取模块、数据预处理模块、数据库、AENNA训练模块、AENNA分类器模块和响应模块。

Figure 3 Intrusion detection model based on AENNA图3 基于AENNA的入侵检测模型

数据捕获引擎模块负责在网络中发送和接收数据包。特征提取模块主要将网络数据包信息转化为包含对应数据包特征值的网络连接记录。数据预处理模块负责将字段数值归一化到一个较小的区间范围，减少由于记录间字段数值差异过大而引发的网络训练不良表现。数据库模块主要是为了方便存储，选用数据库存放预处理模块处理的数据以及通过分类器检测后的结果。AENNA训练模块将从数据库中提取标准的数据(包括给定的样本记录向量和网络训练要达到的目标)对分类器进行训练。AENNA分类器模块可以对输入中的未知的网络连接记录判别为正常或入侵，并做出相应处理。响应模块主要用以接收从AENN分类器检测出的结果，并对入侵行为发出警报。

本文的重点是设计对AENNA分类器，其原理是应用数据及划分后的训练样本集对BP神经网络分类器进行训练，在进化神经网络内部建立起对训练样本的识别模型并存储这些攻击行为的特征模式；然后对捕获的网络数据流进行分析处理，以区分正常的网络行为和异常网络行为；当检测到未知类型的攻击行为时，将其反馈给学习样本库以供BP神经网络进行再学习，从而体现AENNA算法分类引擎所具备的通过学习不断扩展检测范围的能力。

5 实验与结果分析

5.1 实验数据

目前入侵检测研究领域常用的数据集有MITLL、SOTM(Scanofthemonth)、Defcon数据集及由哥伦比亚大学IDS实验室基于MITLL采集整理形成的KDDCUP99数据集。由于MITLL数据集未经格式化处理，数据的攻击特征不规范；SOTM和Defcon数据集中数据无攻击标记，数据筛选比较复杂繁琐；KDDCUP99(简称KDD99)对MITLL数据集的网络流量进行了格式化处理，改进并规范了特征的表示，提供了适用于各种入侵检测算法进行测试和评估的数据集[12]。所以，KDD99网络数据集仍是目前公认的最优秀且影响最广泛的网络安全审计数据集，自公布以来出现了许多基于此数据集的研究成果和研究论文。因此，为了验证AENNA入侵检测算法的检测效果，本文采用KDD99数据集进行检测验证实验。

KDD99数据集是入侵检测领域通用的实验数据集，其中包括四种攻击类型的39种不同攻击的大约500万条连接记录，22种出现在训练数据集中，17种出现在测试集中。四种类型分别是刺探攻击Probe、拒绝服务DOS、获取根权限U2R、远程攻击R2L。

原始数据集中记录数过于庞大，依据各类型所占比例，从KDDdata_10_percent和Correct中提取相应的攻击记录，其中DOS攻击记录约占94%，Probe攻击记录数约占3%，R2L攻击记录数约占2%，U2R攻击记录数约占1%。在攻击集的基础上，选取一部分正常连接记录数据与DOS数据记录，按照1∶3的概率将其混杂入正常数据流量集，形成不均衡数据集。选取49 400个有效数据形成训练集，并选取80 500个数据构成测试集[12]。

数据集中每个网络连接记录中都包含41维数据，利用信息熵理论[13]，计算数据集中每个特征判定网络连接为攻击还是正常状态的信息量，并按信息量大小进行排列，最终选取判定所含信息量较大的前10维特征用于实验，从而实现数据集中连接记录特征的降维，形成了更为高效精简的数据集以用于后续的实验。实验数据的具体构成如表1所示。

Table 1 Composition of experimental data sets表1 实验数据集的组成

5.2 实验测试与结果

实验测试环境为PC机，操作系统为Windows XP、奔腾双核2.0 GHz CPU、2 GB内存，采用Matlab 7.0结合Myeclipse 8.5软件平台在PC机上对AENNA算法进行仿真实现，并利用已实现的算法仿真模块对表1中的KDD实验数据集进行检测验证实验。

首先采用AENNA算法结合实验训练数据集对BP神经网络进行训练，并将训练好的神经网络用于入侵检测，利用实验测试数据集测试其检测性能；其次与将BP神经网络算法、遗传算法、传统进化神经网络算法作为训练算法的训练好的神经网络的检测性能做对比。

为了更容易观察和调整BP神经网络的训练结果，根据实际情况，本文采用仅含有一个隐含层的BP 神经网络。根据2.1节中算法的改进思路，利用大小双种群来优化进化神经网络的隐层节点数，从而确定网络结构。由于Sigmoid 函数是一个连续可微的函数，可以将输入值映射到[0,1]内，方便进化神经网络的处理，可以满足BP 模型对传递函数的连续可微的要求，因此将其作为传递函数。初始权值则通过随机的方法将其置为-10～10 的小随机数。其余的网络权值及阈值则通过改进的自适应进化算法来进行优化。

根据上述规则设定参数，并参考文献[11]，在对AENNA的仿真实现中，网络权值取值区间定义为(-10，10)，将精确度确定为0.01，设置输入节点个数为10，输出节点数为2，误差精度设为±0.01，并设置不同的种群、隐含层节点、进化代数的参数进行对比实验，实验结果如表2所示。

Table 2 Comparison of experimentalresults under different parameters表2 不同参数取值的实验结果比较

由表2可见，当隐含层的节点数为7时，AENNA中个体的适应度在较小的遗传代数后取得最优值。因此，优化后的网络结构为“10-7-2”。将网络权值和阈值作为优化结构后的BP神经网络的初始权值和阈值，输入实验训练样本数据集对其进行训练。样本训练完成后，利用KDD实验测试数据集在已知BP神经网络上进行入侵检测测试，得到的检测结果如表3所示。

Table 3 Intrusion detection results based on AENNA表3 基于AENNA的入侵检测结果

由表2和表3可见，在入侵检测实验中，当种群大小设定为155个、隐含层节点数设定为7层且进化代数设为90次时，基于AENNA的入侵检测效果最佳，此时的误报率和漏报率都相对较小。

为进行训练算法的检测性能对比，根据参考文献[11]中的参数设置，特设定统一的实验参数值，如表4所示。

采用实验中的精简数据集，对BP神经网络算法、遗传算法、传统神经网络进化算法和基于AENNA的入侵检测方法进行检测对比，其中BP神经网络的输入节点数为10，输出节点数为2，隐含层节点设为6，遗传算法的初始种群设为50，适应度函数采用基于误差函数的适应度函数。检测效果对比如表5所示。

Table 4 Parameters setting of comparison test表4 对比实验的参数设置

Table 5 Comparison of intrusion detection performance表5 入侵检测效果比较

从表5中可以清楚地看出，基于AENNA的入侵检测算法不但对已知入侵行为有较高的检测率，而且对于未知入侵行为也有较好的检测率。与采用BP算法、遗传算法和进化BP算法的入侵检测方法相比，AENNA的入侵检测算法有较高的检测率和较低的误报率。

6 结束语

为提高入侵检测系统的检测效率，本文在进化神经网络算法基础上，提出一种自适应进化神经网络算法(AENNA)，以大小两个种群的双种群遗传策略为着眼点，通过改进交叉算子和变异算子的计算方式及公式参数，结合模拟退火算法对遗传算法进行了改进，并利用遗传算法对BP神经网络算法进行网络结构及连接权值优化。通过与其他主流入侵检测算法的检测性能对比实验，表明基于AENNA的入侵检测算法对入侵检测系统的检测性能有较大的提升。由于在遗传算法的改进中引入了模拟退火算法思想，增加了整个算法的时间复杂度，因此下一步研究将解决时间复杂度过高的问题。

[1] Qing Si-han, Jiang Jian-chun, Ma Heng-tai, et al. Research on intrusion detection techniques:A survey[J]. Journal of China Institute of Communications, 2004, 25(7):19-29. (in Chinese)

[2] Wang Qi-an,Chen Bing.Intrusion detection system using CVM algorithm with extensive kernel methods[J]. Journal of Computer Research and Development, 2012,49(5):974-982. (in Chinese)

[3] Wang Tao.Association decision based multiple source network intrusion detection algorithm[J]. Computer Simulation, 2012, 29 (8):120-122. (in Chinese)

[4] Gong Xing-chao, Guan Xin. Intrusion detection model based on the improved neural network and expert system[C]∥Proc of IEEE Symposium on Electrical & Electronics Engineering, 2012:191-193.

[5] Srinivas M, Andrew H. A comparative study of techniques for intrusion detection[C]∥Proc of the 23rd IEEE International Conference on Tools with Artificial Intelligence, 2009:570-577.

[6] Ren Zi-wu, San Ye. Improved adaptive genetic algorithm and its application research in parameter identification[J]. Journal of System Simulation, 2006,18(1):41-66. (in Chinese)

[7] Huang Li-jun, Xu Yong-hua. Solving TSP converged on genetic algorithm and the ant algorithm[J]. Journal of Northeast Agricultural University, 2008,39(4):109-113. (in Chinese)

[8] Li Shu-hui, Ma Li, Xu Xue-zhou. Intrusion detection techniques research based on genetic neural networks [J]. Modern Electronic Technique,2005(5):78-80.(in Chinese)

[9] Yan Yan.A new adaptive genetic algorithm[D]. Harbin:Harbin Engineering University, 2007. (in Chinese)

[10] Yang Wei-bo,Zhao Yan-wei.Improved simulated annealing algorithm for TSP [J]. Computer Engineering and Applications, 2010,46(15):34-36. (in Chinese)

[11] Li Shu-hui. Improved evolutionary neural network algorithm and its applications in intrusion detection[J]. Modern Electronic Technique, 2010, 33(1):78-80. (in Chinese)

[12] Zhang Xin-you, Zeng Hua-can, Jia Lei. Research of intrusion detection system dataset-KDD CUP99[J]. Computer Engineering & Design, 2010,31(2):4809-4813. (in Chinese)

[13] Xu Yong-hua, Li Guang-shui. Incremental SVM intrusion detection algorithm based on distance weighted template reduction and attribute information entropyc [J]. Computer Science, 2012, 39(12):76-78. (in Chinese)

附中文参考文献：

[1] 卿斯汉, 蒋建春, 马恒太,等. 入侵检测技术研究综述[J]. 通信学报, 2004, 25(7):19-29.

[2] 王奇安, 陈兵. 基于广泛内核的CVM算法的入侵检测[J]. 计算机研究与发展, 2012, 49(5):974-982.

[3] 王涛. 基于关联决策算法的网络多源入侵检测[J]. 计算机仿真, 2012, 29(8):120-122.

[6] 任子武, 伞冶. 自适应遗传算法的改进及在系统辨识中应用研究[J]. 系统仿真学报, 2006,18(1):41-66.

[7] 黄立君, 许永花. 遗传算法和蚁群算法融合求解TSP[J]. 东北农业大学学报, 2008,39(4):109-113.

[8] 李淑慧, 马力, 徐学洲. 基于遗传神经网络的入侵检测方法研究[J]. 现代电子技术,2005(5):78-80.

[9] 闫妍. 一种新的自适应遗传算法[D]. 哈尔滨:哈尔滨工业大学, 2007.

[10] 杨卫波, 赵燕伟. 求解TSP问题的改进模拟退火算法[J]. 计算机工程与应用, 2010,46(15):34-36.

[11] 李淑慧. 改进进化神经网络算法及其在入侵检测中的应用[J]. 现代电子技术,2010,33(1):78-80.

[12] 张新有, 曾华粲, 贾磊. 入侵检测数据集KDD CUP99研究[J]. 计算机工程与设计,2010,31(2):4809-4813.

[13] 徐永华, 李广水. 基于距离加权模板约简和属性信息熵的增量SVM入侵检测算法[J]. 计算机科学, 2012,39(12):76-78.

YANGHong-yu,born in 1969,post doctor,his research interest includes network information security.

赵明瑞(1985-),男,河北衡水人，硕士生，研究方向为网络信息安全。E-mail:Zhaomingrui545@163.com

ZHAOMing-rui,born in 1985,MS candidate,his research interest includes network information security.

Intrusiondetectionbasedontheadaptiveevolutionaryneuralnetworkalgorithm

YANG Hong-yu,ZHAO Ming-rui,XIE Li-xia

(School of Computer Science and Technology,Civil Aviation University of China,Tianjin 300300,China)

Aiming at the problem of low detection rate existed in current intrusion detection systems,an adaptive evolutionary neural network algorithm (AENNA) based on the genetic algorithm and the BP algorithm is proposed.Firstly,considering the characteristic of probabilistic jumping property and local search ability in the simulated annealing algorithm,the genetic algorithm is improved.Secondly, using the dual population evolution rule,the algorithm optimizes the weight and the network structure of the BP neural network simultaneously.An adaptive neural network training method is designed through improving the crossover operator and mutation operator of the genetic algorithm.Experimental results show that the AENNA based intrusion detection method can effectively improve the detection rate and reduce the false positive rate.

genetic algorithm;neural network;simulated annealing algorithm;intrusion detection

1007-130X(2014)08-1469-07

2012-12-30;

：2013-04-03

国家自然科学基金资助项目(60776807,61179045)；国家863计划资助项目(2006AA12A106)；天津市科技计划重点项目(09JCZDJC16800)；中国民航科技基金(MHRD201009,MHRD201205)；中央高校基本科研业务费专项(ZXH2009A006)

TP393.08

：A

10.3969/j.issn.1007-130X.2014.08.008

杨宏宇(1969-),男,吉林长春人，博士后，教授,研究方向为网络信息安全。E-mail:yhyxlx@hotmail.com

通信地址：300300 天津市东丽区中国民航大学(北区)6#民航信息技术科研基地

Address:IT Science and Research Base of CAAC,6#,Civil Aviation University of China(North Campus),Dongli District,Tianjin 300300,P.R.China