逻辑及数学演算中的不动项与不可判定命题(Ⅰ)

张金成

(中央党校函授学院，安徽 广德 242200)

自从罗素悖论在数学中出现，围绕着悖论问题，一个多世纪以来，出现了众多的解决方案。然而，这些解决方案，并不能令人完全满意，悖论的数学本质并没有解释清楚，矛盾仍然没有解决。

1931年Gödel证明：如果系统N是一致的，那么，系统N中存在不可判定命题，“系统N”是不能完全的。这就是具有广泛影响的不完全定理。

以下在分析实数集不动点的基础上，可以证明：悖论、不可判定命题可以统一转化成逻辑思维领域中的不动点。不动点广泛存在，Gödel不可判定命题是系统N中的不动点，它与系统N能否完全没有直接关系，一般递归集合中也存在类似Gödel的不可判定命题，因此，Gödel不完全定理的证明是不成立的。

1 正集、反集、不动项

1.1 自指代与不动点

定义1 一般地，函数y=f(x)，x∈R,如果用x取代y，得函数方程x=f(x)，则把x=f(x)叫做y=f(x)的自指代方程。

定义2 如果U是一个集合，f:U→U是一个连续映射，且存在x∈U， 使得f(x)=x,就称x是不动点。

例1 函数f(x)=1-x/3，它的自指代方程是：x=1-x/3，函数f(x)=1-x/3的不动点是方程x=1-x/3的解，即3/4，从图像上看是直线y=1-x/3与y=x的交点。

关于函数不动点有以下Brouwer不动点定理。

Brouwer不动点定理设f:[0,1]→[0,1]是连续映射，则必存在x0∈[0,1]，使f(x0)=x0。

以上是R1中，即1维的Brouwer不动点定理，不动点定理可以推广到2维以及n维欧氏空间中(即：平面上的单位闭圆盘B2具有不动点性质， 即任一连续映射f:B2→B2具有不动点。)

不动点的性质已经不仅仅局限于代数、函数领域，它已经延伸到集合论、离散数学、计算机、经济等其他各个领域。[1]

从函数自指代方程f(x)=1-x/3的不动点分析开始，不动点3/4把实数分成2类性质的实数集合：

大于3/4的实数集合：

R+={x|x>3/4,x∈R}

小于3/4的实数集合：

R-={x|x<3/4,x∈R}

设A(x)为命题：x>3/4，若把不动点3/4扣除，A(x)为命题：x<3/4，即有：

R+={x|A(x),x∈R}

R-={x|A(x),x∈R}

不动点3/4把实数分成2个性质相反的集R+、R-。

1.2 二项划分与双射关系

从以上分析可以看出，实数可以分成2个性质相反的集，满足性质P与不满足性质P的集合。

定义3 设P是U={x1,x2,…,xi,…}上的一个性质，如果性质P把集合U划分成2个集合，满足

+α={x|P(x)∧x∈U}

-α={x|P(x)∧x∈U}

U=+α∪-α

则+α,-α叫做集合U二项划分。

例2 设U={…，-2,-1,0,1,2,…}，即全体整数集合J，设P(x)：x是偶数，则P(x)对U是一个二项划分，即：

+α={x|x=2n,n∈J}

-α={x|x=1-2n,n∈J}；U=+α∪-α

设f是从集合A到集合B的映射，若y=f(x)，x∈A→y∈B，即B中任一元素y，都是A中某元素x的像，则称f为A到B上的满射；若对A中任意2个不同元素x1≠x2，他们的像f(x1)≠f(x2)，则称f为A到B的单射；

定义4 若映射f既是单射，又是满射，则称映射f为A到B的“双射”(或“一一映射”)关系。

函数f:A→B为双射，当且仅当对任意y∈B存在惟一x∈A，满足y=f(x)；映射f为A到B的“双射关系”，记为f:A～B[2]。

例3 在上例中U={…，-2,-1,0,1,2,…}，即全体整数集合的一个二项划分，即：

+α={x|x=2n,n∈J}是偶数集合；

-α={x|x=1-2n,n∈J}是奇数集合；

f(x)=1-x，x∈+α↔f(x)∈-α

f(x)=1-x是二分集合+α,-α上的双射关系，即f:+α～-α。

1.3 正集、反集、不动项

定义5 设U={x1,x2,…,xi,…}为一个集合， 如果U被性质P二项划分为+α,-α，那么：

1)满足性质P的元素x组成的集合，叫做正集，即命题P(x)成立，记为+α={x|P(x)∧x∈U}，正集中的元素叫正项；

2)不满足性质P的元素x组成的集合，叫做反集，即命题P(x)成立，记为-α={x|P(x)∧x∈U}，反集中的元素叫反项；

3)如果正、反集合+α,-α上存在双射关系，即f:+α～-α，则叫+α,-α为正、反对称集合。

例4 设U=Q+为全体正有理数集合，给定一个划分P(x)：x2>2。

正集：平方大于2的有理数集合，即：+α={x|x2>2,x∈Q}；

反集：平方小于2的有理数集合，即：-α={x|x2<2,x∈Q}。

存在双射f:+α～-α对应关系f(x)=2/x，+α,-α是正反对称集合。

例5 设U=(-,0)∪(0,+)，不为0的全体实数集合，给定一个划分P(x)：x>0。

正集：大于0的实数集合，即：

+α={x|x>0,x∈U}=(0,+)

反集：小于0的实数集合，即：

-α={x|x<0,x∈U}=(-,0)

存在双射f:+α～-α对应关系f(x)=-1/x，+α,-α是正反对称集合。

在一个集合U={x1,x2,…,xi,…}上，并不是任意一个划分，都可以构成正反对称集合，有些划分不构成正反对称集合。

构成正反对称集合+α与-α必须满足的2个条件，也可以通俗地表达为：

1)正、反对称集合是不相容的+α∩-α=∅；

2)正、反对称集合可以建立一一对应的函数关系，xi∈+α↔f(xi)∈-α。

下文专门讨论正、反对称集合，不再特别指出。

自指代方程上的不动点的定义可以推广如下：

定义6 1)函数f:A→B，即f为集合A到B的映射，对任意x∈A，y∈B，y=f(x)，把满足自指代方程x0=f(x0)的解x0称为不动项。

2)设U={x1,x2,…,xi,…}为一个集合， 如果U被性质P二项划分为正、反对称集合+α,-α，即f:+α～-α，x满足性质P,f(x)满足性质P，即xi∈+α↔f(xi)∈-α，那么：

如果存在一个x0，满足自指代方程x0=f(x0)元素x0叫正反对称集合上的不动项；由元素x0构成的集合，叫做不动集，记为：e={x|x=f(x)}={x0}。

如果自指代方程x0=f(x0)无解，记为：e={x|x=f(x)}=∅。

例6 设U={…，-2,-1,0,1,2,…}，即全体整数集合，给定一个划分P(x)：x是偶数，对应关系f(x)=1-x。

正集：+α={x|x=2n,n∈J}；

反集：-α={x|x=1-2n,n∈J}；

U=+α∪-α。

不动集：x=1-x，x0=1/2是不动项。

这可以看成从整数到分数的发现。

例7 设U=Q+为全体正有理数集合，给定一个划分P(x)：x2>2，对应关系f(x)=2/x。

这就是从有理数构造无理数的“戴德金分割”。

例8 设U=(-,0)∪(0,+)，不为0的全体实数集合，给定一个划分P(x)：x>0，对应关系f(x)=-1/x。

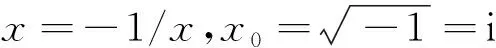
这可以看成从实数到虚数的发现。

“不动项”是通常数学中“不动点”概念的推广，它不再单指是一个点、一个数，它可能是一个点、一个数、一个集合、一个命题等。

对应关系f也不再是单指数之间的运算，而可能是点、集合、或者命题之间的对应关系；

“不动项”和“不动点”都有相同的形式结构x=f(x)，“不动项”比“不动点”具有更广泛的意义。

对不动点，一定有x0∈U，对“不动项”没有U的内外限制，满足x=f(x)的x0存在或者不存在问题，在U外可以找到满足x=f(x)的x0，也是不动项。

定义7 设U={x1,x2,…,xi,…}为一个集合，映射f:U→U，x0满足自指代方程x0=f(x0)。若x0∈U，则元素x0叫U内不动项；若x0∉U，则元素x0叫U外不动项。

不动项元素x0存在，方程x=f(x)有解，且x0∈U，即：存在U内不动项；

U外不动项有2种形式：

1)方程x=f(x)有解，不动项元素x0存在，但x0∉U，即：不动项x0已经构造；

2)方程x=f(x)无解，不动项元素x0不存在，或者说不动项x0没有构造；这种情况，不动集e为空集，e=∅也可以看成U外不动项的特例。

在例1中，设U=R，f:U→U，函数f(x)=1-x/3中，x0=3/4是U内不动项；

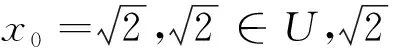
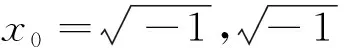
设U=J，f:U→U，函数f(x)=x+1中，x=x+1无解，不动项x0不存在，即第2种情形e=∅。 以后将证明：一个集合U如果能够严格地二项划分成正反对称集合，那么不动项它一定在正反集合之外，即：都是U外不动项，正反对称集合上的不动项有(1)、(2) 2种情形。

f是+α到-α上的一个一一对应关系，满足函数关系y=f(x)，正集+α、反集-α，也可以表示为：

+α={x1,x2,…,xn,…}

-α={f(x1),f(x2),…,f(xn),…}

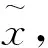
2)若满足x=f(x)，元素x一个特殊的集合，设x=x0，不动集e={x0}。

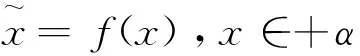
对于P(x)↔当x0满足P(x0)↔P(x0)时，x0即为不动项。

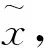
1.4 正、反集对偶变换公理

在以上概念基础上，把矛盾命题重新进行形式描述：

用A+α表示正集+α中的命题A，A-α表示反集-α中的命题A，如：

设+α为欧氏平面上的点集，则-α为非欧平面上的点集，

A+α：在欧氏平面上，过已知直线外一点，只能作惟一一条直线与已知直线平行。

A-α：在非欧平面上，过已知直线外一点，只能作惟一一条直线与已知直线平行。

定义8 在相同集上的否定命题Aα与Aα(即A+α与A+α或A-α与A-α)，叫做经典矛盾命题；在不同集上的否定命题(A+α与A-α或A-α与A+α)，叫做非经典矛盾命题(它与辩证矛盾类似)。

实际上，矛盾命题在不同集上成立，矛盾也就化解了。辩证矛盾就是已经化解或者解释清晰后的矛盾[2]。

由于公式的变化，公理在不同的集中有那些变化，经典逻辑公理在正集中变为：

经典逻辑公理在反集中变为：

由于经典逻辑的公理在正集、反集上都是成立的，今后对2个集上都成立的命题，上标不再区分2个集“+α,-α”，和经典逻辑公式一样不标“+α,-α”。如：A→(B→A)，认为在2个集上都成立。

定义9 正集+α、反集-α的并集U，即：U=+α∪-α，叫做全集。

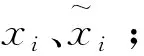
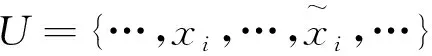
任何一个性质，如果可以对全集形成一个正反对称集划分，如果x0恰恰是性质P划分的不动项，这是一个特殊的命题。

定义10 不动项x0，关于其划分P的性质断定的命题，叫做不动项命题，即命题P(x0)或P(x0)是不动项命题。

如果关于性质M、N、P的不动项记为xM、xN、xP，则M(xM)、N(xN)、P(xP)是不动项命题，并且有P(xP)↔P(xP)。

设命题P是关于正集+α、反集-α的一个划分，即：

若+α={x|P(x)}，则-α={x|P(x)}，f是+α，-α上的一个一一映射，有P(xi)↔

通过一些分析发现P+α与P-α是等价的，例如：欧氏几何与罗氏几何是同构的，它说明一个命题等价于它反集中的否定命题，即应有公理“P+α↔P-α”成立。

根据以上分析，引进一条新公理“P+α↔P-α”或“P(x)↔”。

定义11 称公理“P+α↔P-α” 或“P(x)↔”为“正反集对偶变换公理”。

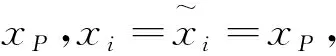
证明：在“正反集对偶变换公理”P(xi)↔中，用xP替换得：P(xP)↔P(xP)。由于正项、反项、不动项定义可以是任何一个集合的元素。如果Xi是一个命题，“正反集对偶变换公理”同样成立，即有：

P(Xi)↔当Xi=XP是不动项时，有：P(XP)↔P(XP)[3]。

1.5 悖论是正、反集上的不动项

在“正反集对偶变换公理”P(xi)↔中，这并不矛盾，但是，当时，即：x0为不动点时，有P(x0)↔P(x0)就表现为悖论。

在例 1中，对于一个确定的实数a：

如果a>3/4⟹-a/3<-1/4⟹1-a/3<3/4⟹则f(a)<3/4，即：A(a)→A(f(a))；

如果a<3/4⟹-a/3>-1/4⟹1-a/3>3/4⟹则f(a)>3/4，即：A(a)→A(f(a))。

由于a=f(a)，这就形成了类似悖论命题A(a)↔A(a)，这个悖论的解就是：a=3/4。

一般地，设f是R上的一个一一映射，f:R→R，如果性质P是R上的一个二项划分，对任意一个x，x满足性质P，f(x)满足性质P，即R+={x|P(x),x∈R}，R-={x|P(x),x∈R}，x∈R+↔f(x)∈R-，P(x)↔P(f(x))。

不动点x0把实数集合分成正、反集合，其中一个集合中的元素满足性质P，另一个集合中的元素满足性质P，而不动点x0可以看成具有2个矛盾性质P与P的点，即P(x0)↔P(f(x0))，这就是悖论形成的内在机理。

在例 4中，设P(x)表示命题x2>2，对于一个确定的数a：

P(a)：a2>2⟹a2=4/a2

4/a2>2⟹a2<2⟹P(a)

4/a2<2⟹a2>2⟹P(a)

由于a=f(a)，这就形成了类似悖论命题P(a)↔P(a)，这个悖论的解就是：

在例 5中，设P(x)表示命题“x>0”，对于一个确定的数a：

P(a)：a>0⟹a=-1/a，

-1/a>0⟹a<0⟹P(a)；

所以，得到悖论：P(a)↔P(a)；

例9 罗素悖论中的集合分为2类：

一类集合是自身的元素，即x∈x，+α={x|x∈x}；

现在构造第2类集合全体组成的集合(即-α)，用R={x|(x∈x)}表示，即x∈R↔(x∈x)，问集合R是那类集合？即用R去自指代。

无论集合R是那类集合，即得到罗素悖论：R∈R↔(R∈R)。

设P(x)表示命题x∈x，+α={x|P(x)}，则P(x)表示命题(x∈x)，-α={x|P(x)}。

第2类集合全体组成的集合R={x|P(x)}；

即x∈R↔P(x)⟹R∈R↔P(R)；

即P(R)↔P(R)。

所以，R={x:x∉x}是关于谓词P(x)的不动项，即罗素悖论是不动项命题[3]。

1.6 逻辑演算中的不动项

在“正反集对偶变换公理”P+α↔P-α中，当存在不动项时，就存在悖论。如果把“正反集对偶变换公理”P+α↔P-α引进逻辑演算系统中，逻辑演算系统中就会同样存在悖论。

在命题演算系统L中，如果承认“正反集对偶变换公理”P+α↔P-α，则不动项存在，存在悖论。即若+α=-α=e，则┝Pe↔Pe；

在谓词演算系统L中，如果承认“正反集对偶变换公理”P(xi)↔则有不动项存在，存在悖论；即若则┝P(xP)↔P(xP)。

由于在经典系统中，定理Pe,Pe┝B成立，所以，如果承认悖论存在，无论是系统L还是系统K，会导致整个系统崩溃。

在以前的命题逻辑系统L，谓词逻辑系统K中，为什么没有发现不动项的存在，是因为在其中没有建立起来正反演算，一个公理系统中是否存在不动项(悖论)，跟演算方式有关。

由于不动项、悖论的存在，是不是“命题逻辑系统L”、“谓词逻辑系统K”都是不足道的，是一个崩溃的逻辑系统？以后的证明表明：“命题逻辑系统L”、“谓词逻辑系统K”都是在已知集合U上的封闭演算，其中的不动项都是U外不动项。U外不动项的存在是正常的，它不会导致“命题逻辑系统L”、“谓词逻辑系统K”崩溃。[4]

1.7 自然数系统中的一般不动项

已经证明，命题逻辑系统L演算中存在不动项；谓词逻辑系统K演算中存在不动项；同理，自然数系统N演算中也存在不动项。

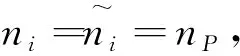
证明设N={0,1,2,3,…}，构造N的子集合U，U⊆N，命题P是关于正集+α、反集-α的一个划分，U=+α∪-α，即：若+α={n|P(n)}，则-α={n|P(n)}，f是+α，-α上的一个一一映射，有P(n)↔

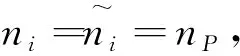
或P(nP)↔P(nP)；以后也将证明：自然数系统N演算中的不动项，也是U外不动项。

由于自然数系统N是一个具体的数学系统，已经不需要正反集对偶变换公理P+α↔P-α，只要进行类似正反集对偶变换的运算(即自指代运算)，就会产生不动项。

在自然数系统N中，设U={n1，n2，…，ni,…}。┝NP(xP)↔P(xP)具有一般性，性质P可以是任何一个性质。

如果P(x)表示：x是偶数；

那么P(nP)↔P(nP)表示：nP是偶数↔nP是奇数。

如果设U表示自然数系统N中的所有命题，P(x)表示：x可以证明；即x是系统N可证命题，┝Nx。

那么P(nP)↔P(nP)表示：nP可以证明↔nP不可以证明。

构造函数f(x)=11-x，若x∈[0,11]⊂N，则f(x)∈[0,11]⊂N；

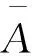
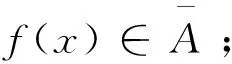
设P(n)表示：n是偶数；则P(n)表示：n是奇数；

P[n]↔P[f(n)]；

让f(n)=11-n自指代，即：n=f(n)，n=nP是它的不动项；

则得到：P(nP)↔P(nP)。

承认正反集对偶变换公理P+α↔P-α，命题逻辑系统L演算中存在不动项；谓词逻辑系统K演算中存在不动项；自然数系统N演算中也存在不动项，不动项及不动项命题的存在是不可否认的。

正、反集对偶变换公理P+α↔P-α产生不动项的本质是自指代，也就是说，只要允许自指代，就可能产生不动项，悖论就不可能避免。

2 U外不动项的逻辑性质

2.1 正反对称集上的不动项一定是U外不动项

对于一个全集U={x1,x2,…,xi,…}，P是一个划分标准，如果性质P可以把U划分成正、反2个对称集。

定理3(U外不动项定理) 设全集U={x1,x2,…,xi,…}是一个已经定义的集合，U可以二分成正反对称集合U=+α∪-α，如果正集、反集上的演算是一致的，那么，不动项xP不属于正集+α，也不属于反集-α，即xP∉U；即：正、反集合上的不动项，是U外不动项。

证明

1)├xP∈+α

┈┈假设；

2)├P(xP)↔P(xP)

┈┈不动项定理；

3)├P(xP)∧P(xP)┈┈经典定理，正集+α中存在矛盾命题，这与正集是一致的相矛盾；

4)├xP∉+α

┈┈(1)，反证法；

同理可证：xP∉-α。

即如果不动项属于正集+α，那么，将导致正集矛盾；同样，如果不动项属于反集-α，那么，将导致反集矛盾；所以，不动项不属于正集+α，也不属于反集-α，即xP∉U。

例11 从整数到分数的发现：U为全体整数集合J，把这个集合，分成偶数集合与奇数集合。

+α={x|x=2n,n∈U}偶数集合；

-α={x|x=1-2n,n∈U}是奇数集合。

正反集对应函数f(x)=1-x；x=f(x)，x=1-x，x=1/2，所以，1/2为不动项，但是，1/2∉+α，1/2∉-α，1/2∉U，即：1/2为U外不动项，1/2不再是整数。

例12 从有理数到无理数的发现：U为全体正有理数集合Q+。

+α={x|x2>2,x∈U}

-α={x|x2<2,x∈U}

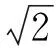
例13 从实数到虚数的发现：U为不为0的全体实数集合R。

+α={x|x>0,x∈U}

-α={x|x<0,x∈U}

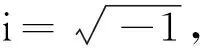
进一步可以探明：凡是通过自指代方程x=f(x)形成的正、反集合上的不动项，都存在类似的性质，是U外不动项，既不在正集中，也不在反集中。

U外不动项xP，不具有原集合U的性质，是变异项。

根据U外不动项定理3，设U=+α∪-α，如果存在正、反集合上的不动项，那么，它们都是U外不动项，由这个定理，很容易得到以下推论：

推论1U=+α∪-α，P是U的一个分割，任何悖论P(xP)↔P(xP)其中项xP是U外不动项。

推论2U=+α∪-α，+α={x|x∈x}，-α={x|(x∈x)}，罗素悖论P(R)↔P(R)，R={x:x∉x}是U外不动项。

推论3U=+α∪-α，+α={P|V(P)=1}，+α={P|V(P)=0}，Pe↔Pe命题演算系统L上的不动项Pe，是U外不动项。

推论4U=+α∪-α，P是U的一个分割，P(xP)↔P(xP)谓词演算系统K上的不动项xP，是U外不动项。

推论5N={0,1,2,3,…}，U⊆N，+α={n|P(n)}，-α={n|P(n)}，P(nP)↔P(nP)自然数系统N上的不动项nP，是U外不动项。

定理4 设全集U={x1,x2,…,xi,…}是一个已经定义的集合，不动项xP具有正集+α性质P(x)，也具有反集-α性质P(x)，不动项xP具有双重性质，同时与正集+α性质P(x)相矛盾，也与反集-α性质P(x)相矛盾。

证明：

1)├P(xP)↔P(xP)

┈┈不动项定理

┈┈(1)，经典定理

3)├P(xP)∨P(xP)

┈┈(2)，经典定理

4)├P(xP)

┈┈(3)

不动项xP具有正集+α性质P(x)；

5)├P(xP)→P(xP)

┈┈(1)，经典定理

┈┈(5)，经典定理

┈┈(6)，

不动项xP也具有反集-α性质P(x)；

8)├(P(xP)→P(xP))∧(P(xP)→P(xP))

┈┈(1)，经典定义

┈┈(8)经典定理

定义12 设全集U={x1,x2,…,xi,…}是一个已经定义的集合，不动项不属于正集+α，也不属于反集-α，即不动项不属于已定义的集合，xP∉U，单独给不动项命名一个集，叫做相对于U的未定义集，即：不动集e={xP}；不动项xP叫做相对于U的未定义项；如果xP是未定义项，P是U上的一个谓词，那么P(xP)叫做未定义命题。

正、反对称集合+α,-α是相互矛盾的集合，通常矛盾集合中的项是不能进行自指代的，当进行自指代时，满足x=f(x)的项xP，在U中不存在；

如果存在xP满足x=f(x)，就会发生变异，xP在U中无定义，只能把U拓展到U外定义xP，所以，U外不动项xP，也称为变异项。

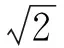
按照以上定义，U外不动项xP相对于已经定义集合U，都是未定义项；所以，悖论(包括罗素悖论)，命题演算系统L上的不动项Pe，谓词演算系统K上的不动项xP，自然数系统N上的不动项nP，相对于它们原始的已定义集合U，都是未定义项。

2.2 U外不动项命题的不可判定性

定理5U外不动项命题P(xP)或P(xP)，相对于任何一致系统都是不可判定命题。

证明假设存在某个一致系统H，若H┝P(xP)，P(xP)↔P(xP)，则H┝P(xP)，与系统H是一致的相矛盾，所以，H┝P(xP)；

假设H┝P(xP)，P(xP)↔P(xP)，则H┝P(xP)，与系统H是一致的相矛盾，所以，H┝P(xP)；

所以：P(xP)，P(xP)在系统H均不可证，P(xP)是系统H的不可判定命题；

当用一个性质P去划分一个系统时，在正集与反集的边缘都会产生不动项，这个不动项命题，无论在任何系统中，都是不可判定的。

对于任意关于谓词N的不动项XN，关于性质M命题M(XN)，若M≠N，则M(XN)不是不动项命题。若M=N，则M(XN)是不动项命题，因此是不可判定的。

定义13U外不动项命题P(xP)的不可判定性，叫做U外不可判定命题。

例15 从整数到分数的发现：U为全体整数集合，把这个集合，分成偶数集合与奇数集合，

+α={x|x=2n,n∈U}偶数集合；

-α={x|x=1-2n,n∈U}是奇数集合。

正反集对应函数f(x)=1-x；，x=1-x，1/2为不动项。

如果设P(x)表示命题：“x是偶数”；则有不动项命题P(1/2)，P(1/2)都是U外不可判定命题。

从有理数到无理数的发现：U为全体有理数集合。

+α={x|x2>2,x∈U}

-α={x|x2<2,x∈U}

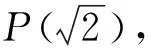
从实数到虚数的发现：U为不为0的全体实数集合。

+α={x|x>0,x∈U}

-α={x|x<0,x∈U}

如果设P(x)表示命题：“x>0”；则有不动项命题P(i)，P(i)都是U外不可判定命题。

按照定理5，所有正、反集合上的不动项命题，都是U外不可判定命题。由这个定理，很容易得到以下推论：

推论6 任何悖论都是U外不可判定命题。

推论7 罗素悖论是U外不可判定命题。

推论8 命题演算系统L上的不动项命题Pe，是U外不可判定命题。

推论9 谓词演算系统K上的不动项命题P(xP)，是U外不可判定命题。

推论10 自然数系统N上的不动项命题P(nP)，是U外不可判定命题。

2.3 U外不可判定性与系统的完全性无关

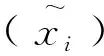
证明假设存在一个一致的公理系统∑，使得∑┝P(xi),(i=1,2,…)，即命题P(xi)在公理系统∑中都可证；

由于命题P(xP)↔P(xP)， 若∑┝P(xP)则∑┝P(xP)，与公理系统∑一致性相矛盾；

所以，P(xP),P(xP)在公理系统∑中是不可判定命题。

由于命题P(xP)↔P(xP)，若∑┝P(xP)则∑┝P(xP)，与公理系统∑一致性相矛盾；

所以，同样有P(xP),P(xP)在公理系统∑中是不可判定命题。

这个U外不动项命题P(xP)，是恒成立不可判定命题，与U内项命题P(xi)在公理系统∑中是否可证没有关系。

如例15，从整数到分数的发现：U为全体整数集合，把这个集合，分成偶数集合与奇数集合。

+α={x|x=2n,n∈U} 偶数集合

-α={x|x=1-2n,n∈U} 奇数集合

正反集对应函数f(x)=1-x；，x=1-x，1/2为不动项，“1/2是偶数”；“1/2是奇数”；均不可证，都是不可判定命题。这个U外不动项命题，它与其他整数xi是偶数还是奇数是否可证没有关系，是U外不可判定命题。

由于一般的可判定集合外也存在不动项，所以，不动项命题的不可判定，是U外不可判定命题，并不影响集合U内命题的可判定性。

由于不动项命题的不可判定，不影响集合的递归性，所以，它也不影响系统的完全性。

传统系统完全性的定义是：设全集UΣ={X1,X2,…,Xi,…}是系统Σ上的全部命题。

1)若∀Xi∈UΣ，(Σ┝Xi)∨(Σ┝Xi)，即：若∀Xi∈UΣ，Xi或Xi在Σ中可证明，就称UΣ相对Σ是完全的，简称系统Σ是完全的；

注：系统Σ完全性的另一个等价定义是：若∀Xi∈UΣ，则MΣXi⟺Σ┝Xi，称系统Σ是完全的(MΣ是系统Σ的模型)。

定理7U外不动项命题P(xP)的不可判定性，不能作为系统Σ是否完全的标准，即U外不动项命题的不可判定性与系统Σ完全性无关。

证明设全集UΣ={X1,X2,…,Xi,…}是系统Σ上的全部命题，在系统Σ一致的假设下，用P(X)表示Σ┝X；P(X)表示ΣX。可证关系P把UΣ划分成正、反2个集合：+α={X|P(X)}；-α={X|P(X)}。建立双射关系F:+α～-α，F(X)=X，如果有不动项XP存在，P(XP)↔P(XP)，即：(Σ┝XP)↔(ΣXP)，那么P(XP),P(XP)在系统Σ中是不可判定命题，但是，它们是U外不可判定命题，XP∉UΣ。

根据“系统Σ完全性”的定义，“系统Σ完全性”只跟UΣ内的命题X是否可证有关系，因为XP∉UΣ，所以，“系统Σ完全性”根XP是否可证，没有关系。

不动项XP不在+α中，也不在-α中，是U外不动项，系统的完全性只与U内的项判定有关。即：P(XP),P(XP)不可判定，+α={X|P(X)}，-α={X|P(X)}中的命题仍然是可判定的。

另外，U外不动项命题P(xP)的不可判定性，能作为系统Σ是否完全的标准，那么不动项命题P(xP)的不可判定，∑相对U是不能完全的。我们可以找到这样一个实例，一个完全的系统中，同样存在不动项。

事实上，由于不动项存在是普遍的，很容易在整数、自然数的任意一个有限子集上找到不动项。如果U外不动项命题P(xP)的不可判定，可以作为系统∑完全性、正反集合递归性的标准；那么将建立不起来真正完全的系统，也找不到真正的递归集合，这显然是错误的。

由于以前的逻辑研究中没有发现不动项，关于系统完全性的定义是有缺陷的，容易把UΣ外不动项XP与UΣ中的命题相混淆，把UΣ外不动项XP与UΣ中的命题区别开，系统完全性定义修改如下：

定义14 设全集UΣ={X1,X2,…,Xi,…}是系统Σ上的全部命题。

1)若∀Xi∈UΣ，(Σ┝Xi)∨(Σ┝Xi)，即若∀Xi∈UΣ，Xi或Xi在Σ中可证明，就称UΣ相对Σ是完全的，简称系统Σ是完全的；

2.4 U外部矛盾的永恒性及其来源

“不动项定理”说明只要有不动项存在，就会有悖论存在，就会有矛盾存在。

推论11 设全集U={x1,x2,…,xi,…}是一个已经定义的集合，如果U可以二分为正反集合，并且存在不动项，那么必然会形成不动项矛盾(即悖论)。

例16 设U1为不包含0的整数集合，+α1={x|x>0,x∈J}，-α1={x|x<0,x∈J}，U1=+α1∪-α1。

设P1(x):x>0，正反集对应函数f(x)=-x；x=f(x)，x=-x，x=0，e1={0}

由于0是不动项，所以，┝P1(0)↔P1(0)；┝P1(0)∧P1(0)，这里发现0是正负数外的一个矛盾数。

如果再把e1={0}加进原来集合U1，扩展到全部的整数集合U2=J，再构造奇数、偶数正反集合。

设+α2={x|x=2n,n∈J}，-α2={x|x=1-2n,n∈J},U2=+α2∪-α2=J。设P2(x):x=2n,n∈J即：是偶数，正反集对应函数f(x)=1-x；x=f(x)，x=1-x，x=1/2，由于1/2是不动项，所以，┝P2(1/2)↔P2(1/2)；┝P2(1/2)∧P2(1/2)。这里发现1/2是奇数、偶数外的一个矛盾数。

矛盾数的出现相对于原来的已知集合U1是一个未定义项，当把这个矛盾数重新定义，并且扩展的原来的已知集合U1中去时得到U2，当以U2为整体已知集合时，原来的矛盾就退化、消融了，但是，以U2为已知集合构造正反集合，在U2之外又有新的矛盾数出现，再把这个矛盾数重新定义，并且扩展的原来的已知集合U2中去时得到U3，当以U3为整体已知集合时，矛盾又退化、消融了，…，如此，数系在矛盾的出现与消融中扩展，外部矛盾总是存在的，是永恒的。

根据“U外不动项定理”：如果全集U={x1,x2,…,xi,…}是一个已经定义的集合，如果正集、反集上的演算是一致的，那么，不动项xP不属于正集+α，也不属于反集-α；即正、反集合上的不动项，是U外不动项。即xP∉+α，xP∉-α，xP∉U。

“U外不动项定理”说明不动项一定存在U外，即不动项矛盾(悖论)来源于正反集合之外。

推论12 设U={x1,x2,…,xi,…}，如果U上的演算是一致的，那么，不动项矛盾“┝P(xP)↔P(xP)”，┝P(xP)∧P(xP)在U外，即xP∉U(矛盾来源于已定义集合U的外部)。

U1分成对立集合U1=+α1∪-α1，产生矛盾集合e1，重新命名不动项，扩展U2=+α1∪e1∪-α1；

U2分成对立集合U2=+α2∪-α2，产生矛盾集合e2，重新命名不动项，扩展U3=+α2∪e2∪-α2；

U3分成对立集合U3=+α3∪-α3，产生矛盾集合e3，重新命名不动项，扩展U4=+α3∪e3∪-α3；

…

Un分成对立集合Un=+αn∪-αn，产生矛盾集合en，重新命名不动项，扩展Un+1=+αn∪en∪-αn；

…

以上分析发现经典逻辑是一个在相对已知集合上二分的封闭思维系统，在这个已知集合的外部可以产生矛盾，产生悖论，而且这种矛盾是无法避免的。如果Un上的演算是一致的，矛盾只会产生在Un的外部，经典逻辑在Un上的演算仍然成立，外部矛盾不会导致系统崩溃。这说明，Un的外部矛盾是一种恒存在的矛盾，是正常的。

3 Gödel不完全定理证明不能成立

3.1 Gödel不可判定命题

简单回顾一下Gödel不完全定理的证明过程：

定义15 一个自然数集上的k元关系R，称为在N中可表达的，如果存在一个有k个自由变元的公式ξ(x1,x2,…,xn)，使得对任何自然数n1,n2,…,nk，

1)如果R(n1,n2,…,nk)在N中成立，则┝Nξ(0(n1),0(n2),…,0(nk))；

2)如果R(n1,n2,…,nk)在N中不成立，则┝Nξ(0(n1),0(n2),…,0(nk))[3]。

引进一个二元关系W：W={(m,n)}，m是公式U(x)的Gödel数，n是公式U(m)从N证明的Gödel数。

可以证明：递归关系在N中都是可以表达的。

可以证明：二元关系W是递归的，所以，W={(m,n)}在N中是可表达的：

(m,n)∈W⟹┝Nw(0(m),0(n))

(m,n)∉W⟹┝Nw(0(m),0(n))

U(x)=∀yw(x,y)---构造公式U(x)；

m=g(U(x))；m是公式U(x)的Gödel数；

用m去替换U(x)中所有自由出现的x得：

U(m)=∀yw(0(m),y)-----y是U(m)证明的Gödel数；

∀yw(0(m),y)的解释是“对任意y，y是U(m)证明的Gödel数不成立”或者；

“对任意y，y是Gödel数为m的公式(即：U(m))证明的Gödel数不成立”；

或者∀yw(0(m),y)↔∃y┝w(0(m),y) “不存在y，y是U(m)证明的Gödel数”，即“U(m)是不可证明的”[4]；

定理8U(m)在N中是一个不可判定命题。

证明

1)(m,n)∈W⟹┝Nw(0(m),0(n))，

(m,n)∉W⟹┝Nw(0(m),0(n))；

2)┝NU(m)

-----假设，

3)┝N∀yw(0(m),y)-----把U(m)从N证明的Gödel数记为n，则(m,n)∈W，

4)┝Nw(0(m),0(n))

-----(3)，(1)，

5)┝Nw(0(m),0(n))

-----(3)，K4，MP，

-----(4)，(5)矛盾；

7)┝NU(m)

-----假设，

8)┝N∀yw(0(m),y)↔∃yw(0(m),y)

-----(7)，

9)U(m)在N中不成立，任意n，(m,n)∉W，

10)┝Nw(0(m),0(n))

-----(1)，(9)，

11)┝Nw(0(m),0(n))

-----(8)

设n是U(m)从N证明的Gödel数，

-----(10)，(11)矛盾，

13)U(m)，U(m)都是不可证命题，即，U(m)在系统中是不可判定的

-----(6)(12)。

以上不可判定命题U(m)的构造与证明是由Gödel在1931年给出的，在一般的数理逻辑文献及[4，10]中都可以找到。

3.2 Gödel不可判定命题是U外不动项

定理9 设G(X)表示谓词┝NX，Gödel不可判定命题U(m)是关于G(X)的不动项。

证明设U={自然数系统N上的全部命题}，用系统N上的可证性质G，把U二分成正反对称集合。

1)设

+α={U(x)|∃nw(m,n),m=g(U(x))}

用谓词G(X)表示┝NX，+α={U(x)|G(U(x))}正集中U(x)都是系统N上可证明公式，即：┝NU(x)；

2)设

-α={U(x)|∀nw(m,n),m=g(U(x))}

-α={U(x)|G(U(x))}

反集中U(x)都是系统N上不可证明公式，即：NU(x)，正反集合的元素都是命题。

3)在系统N一致的前提下，X是可证命题，则X一定是不可证命题。构造正反集合双射关系，Y↔F(X)=X，

正集，反集有对应关系X∈+α↔Y∈-α，G(X)↔G(Y)或者G(X)↔

4)构造自指代方程X↔F(X)，X↔X，G(Xi)↔这个命题方程是否存在不动项？ödel不可判定命题U(m)，恰恰是满足它的解；

5)构造公式U(x)，U(x)=∀yw(x,y)；

6)设m=g(U(x))；m是公式U(x)的Gödel数；

7)用m去替换U(x)中所有自由出现的x得：

U(m)=∀yw(0(m),y)-----y是U(m)证明的Gödel数，U(m)↔G(U(m))；

8)若┝NU(m)，即G(U(m))成立，

则┝NG(U(m))；

10)G(U(m))↔G(U(m))，

G(Xi)↔的解；

11)U(m)是关于命题

G[U(m)]↔G[U(m)]的不动项(这个不动项是命题)；

由于正反对称集合上的不动项都是U外不动项，所以，很容易得到以下推论。

推论13 设+α={U(x)|G(U(x))}，

-α={U(x)|G(U(x))}，U=+α∪-α，Gödel不可判定命题U(m)，是U外不动项。

Gödel不可判定命题是不动项(逻辑上的项具有一般意义，可以是任何一个集合的元素，如：点，数，命题等)，也可以把G[U(m)],G[U(m)]看成一个二阶命题，对偶变换公理是一般的逻辑规律，对二阶命题同样成立；或者利用Gödel数，U(m)也可以转化成一个数，即转化成一阶语言中的普通项。[5]

3.3 Gödel不完全定理的证明不成立

以上讨论并证明了“U外不动项”的一般逻辑性质，概括如下：

1)正、反集上的不动项一定在U外(定理3)；

2)U外不动项相对于U是未定义项(定理4)；

3)U外不动项命题是不可判定命题(定理5)；

4)U外不动项命题的不可判定与U内项在系统中是否可以判定无关，与系统的完全性无关(定理6、7)；

5)U外不动项矛盾是永恒的矛盾，矛盾来源于U外(推论11、12)；

以上证明Gödel构造的不可判定命题，也是系统N中的一个不动项，它也满足以上一般逻辑性质，因此，Gödel关于不完全性定理的证明是错误的。

将修正后的系统完全性定义14，推广到自然数系统N上：

定义16 设全集UN={X1,X2,…,Xi,…}是自然数系统N上的全部命题，。

1)若∀Xi∈UN，(┝NXi)∨(┝NXi)，即若∀Xi∈UN，Xi或Xi在N中可证明，就称自然数系统N是完全的；

注：XG是UN外的不动项，以上定义中特别列出(3)，是为了防止把XG与UN中命题混淆，系统的完全性与UN外的项无关，与UN内的项有关。

定理10 Gödel不可判定命题U(m)，U(m)在系统N中不可判定，是U外不可判定命题，与系统N的完全性无关。

证明

1)XG=U(m)是满足方程

G(XG)↔G(XG)的解，

即：G(U(m))↔G(U(m))，

U(m)是关于命题公式G[U(m)]↔G[U(m)]的不动项；

2)不动项命题G(XG)的不可判定，是U外不可判定命题，不能作为N是否完全的标准；

3)不动项U(m)的不可判定性与系统N相对于UN完全性无关；Gödel不可判定命题U(m)，是U外变异项。

所以，Gödel关于自然数系统N的不完全定理的证明是错误的。

这个U(m)是恒成立不可判定命题，是U外不可判定命题，与U内项命题Xi在公理系统N中是否可证没有关系；

不动项U(m)的不可判定，

+α={U(x)|G(U(x))}，

-α={U(x)|G(U(x))} 的Gödel数集合仍然可能是递归集合。

很容易得到以下推论：

推论14U(m)在系统N中不可判定，是U外不可判定命题，与系统N的定理集合的可判定性无关。无论在系统N中怎么添加公理，这个不可判定命题U(m)是消除不了的，因为U(m)是一个不动项，已经不是系统N的一个命题。如果我们仔细观察不完全定理的证明过程，不可判定命题U(m)的构造，只与系统N的可表达有关，与系统N的公理无关，也就是说：即使系统N一条公理也没有，不可判定命题U(m)照样存在。这个U(m)是恒成立不可判定命题，与公理系统N是否可以完全没有直接关系。

以后将证明：不光Gödel不可判定命题是U外不动项，“Cantor对角线证明方法”所产生的项，也都是U外不动项，“Cantor对角线证明方法”是错误的证明方法。

参考文献:

[1]陈汝栋. 不动点理论及应用[M].北京：国防工业出版社，2012： 1-4.

[2]戴牧民，陈海燕.公理集合论导引[M].北京:科学出版社，2011： 15-17.

[3]张金成. 容纳矛盾的逻辑系统与悖论[J]. 系统智能学报，2012(3)： 208-209.

ZHANG Jincheng. A logic system which accommodates contradictions and paradoxes[J]. CAAI Transactions on Intelligent Systems, 2012(3)： 208-209.

[4]HAMILTON A G. Logic for Mathematicians[M]. Cambridge of University, 1978： 29-40， 82-92.

[5]李未.数理逻辑[M].北京：科学出版社， 2008： 105-110.

[6]张立昂.可计算性与计算的复杂性[M].北京大学出版社, 2011： 80-85.

[7]S.C 克林 著 莫绍揆 译. 元数学导论[M]. 北京：科学出版社 1984： 4-12

[8]何华灿. 泛逻辑学原理[M].北京：科学出版社，2001： 1-15.

[9]Boolos. 可计算性与数理逻辑[M]. 北京： 电子工业出版社; 2002： 152-160.

[10]汪芳庭.数理逻辑[M]. 北京：科学出版社, 2001: 159-163.