改进蛙跳算法的LQR控制器的优化设计

彭勇，陈俞强,2

(1.东莞职业技术学院 计算机工程系,广东 东莞 523808； 2.广东工业大学 自动化学院,广东 广州 510006)

线性二次型调节器(linear quadratic regulator，LQR)是以状态变量和控制变量二次型函数的积分作为目标函数的最优控制系统[1]。

倒立摆系统是一个典型的高阶次、不稳定、多变量的非线性控制系统。自动控制系统的稳定性、可控性、收敛速度、抗干扰能力等抽象的控制概念都可以通过倒立摆系统直观、形象地表现出来，所以倒立摆是自动控制领域中较为理想的实验平台。自适应、状态反馈、智能控制、模糊控制及人工神经元网络等多种控制理论都可以通过倒立摆系统来加以验证，所以通过倒立摆系统来对利用蛙跳算法进行LQR优化控制的效果进行验证[2]。

1 单级倒立摆系统数学模型的建立

假设线性时不变系统的状态方程模型为

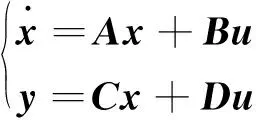
可以引入最优控制的性能指标，既设计一个输入量u，使得式(1)最小。

(1)

式中：Q和R分别为状态变量和输入变量的加权矩阵，tf为控制作用的终止时间。矩阵S对控制系统的终值给出某种约束，这样的控制问题称为线性二次型最优控制问题[3]。

对于倒立摆系统来说，如果忽略了空气阻力和各种摩擦之后, 可将直线一级倒立摆系统抽象成沿着光滑导轨运动的小车和通过轴承连接的匀质摆杆组成。如图1所示[4]。其中, 小车的质量为M，摆杆质量为m，摆杆长为l，F为作用于小车上的外力，μ为小车摩擦系数，I为摆杆转动惯量，x为小车的位移，摆杆角度为θ，重力加速度为g。

图1 单级倒立摆的结构简化模型Fig.1 The model of inverted pendulum system

倒立摆控制系统本质上是一个不稳定系统，如果不给小车施加牵引力以使小车做适当运动，倒立摆就不能保持倒立位置而向左或向右倾倒，系统控制的目的就是让小车在轨道上来回运动，以保持摆杆树立不倒。

至为了使系统模型不过于复杂，先进行几点假设：1)摆杆及小车均为刚体且摆杆为匀质刚体；2)忽略小车运动时所受摩擦力和摆杆转动时所受的摩擦力矩[2,4]。

得到系统的动力学方程组为

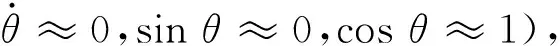
令作用力、位移与角度参数为时间的函数有

于是最终得到方程组为

即系统的状态变量为

则系统状态空间表达式为

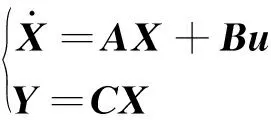
式中：

根据单级倒立摆系统的状态方程，由于终端时间tf=，系统的二次型性能指标为

式中：e(t)=yr-y(t)，yr为系统期望输出；Q和R分别为输出误差变量和输入变量的加权矩阵，决定了系统误差与控制能量消耗之间的相对重要性(Q为半正定对称矩阵；R为正定对称矩阵)。找一状态反馈控制律：u=-Kx，使得二次型性能指标最小化。

由线性二次型最优控制理论可知，若想最小化J，则控制信号应该为

u*=-R-1BTPx

式中：P为对称矩阵，该矩阵满足Riccati微分方程：

易知，状态变量x与Riccati微分方程的解P将决定最优控制信号。

在实际工程中，系数矩阵A、B、C、R多为常数矩阵，而且系统在tf→时趋于稳定，微分方程的解矩阵P将趋于0，使得则Riccati微分方程简化为Riccati代数方程：

PA+ATP-PBR-1BTP+Q=0

则最优反馈系数矩阵K=R-1BTP。

用MATLAB求解LQR(A,B,Q,R)可以求出最优反馈系数矩阵K的值。LQR函数需要选择2个参数R和Q，这2个矩阵是用来平衡输入量和状态量的权重，R一般选择一常量，Q是一个对角线矩阵，一般情况下由元素Q1,1和Q3,3来确定，其他元素项为0。其中，Q1,1代表摆杆角度的权重，而Q3,3是小车位置的权重。所设计的最优控制完全取决于加权系数Q1,1和Q3,3的选择。在以往的设计中, 权重往往是由设计者根据其经验经过反复试验获得的, 需要设计者根据系统输出逐步调整权重矩阵，直到获得满意的输出响应值为止。这样不仅费时，而且也无法保证获得最优的权重矩阵，因此获得的最优控制反馈系数不能保证使系统达到最优。

2 改进蛙跳算法优化LQR参数

混合蛙跳算法(shuffled frog leaping algorithm，SFLA) 在解空间中模拟青蛙群体在寻找食物时的行为探索问题的最优解，是 Eusuff 和 Lansey[5]为解决组合优化问题于 2003 年提出的一种群智能算法。SFLA 结合了 PSO 算法和 Memetic 算法的优点[6]，具有易理解、易实现及寻优能力强等优势。其中，Memetic 是以遗传行为为基础，通过启发式搜索解决优化问题的一种群智能算法。Memetic 算法的特征是可以在进化之前通过局部搜索获得一些经验。

2.1 改进蛙跳算法的实现

2.1.1 标准蛙跳算法[7]

1)初始化：选择Nm和Nf，令Nm为青蛙子群memeplex的个数，Nf为每个子群memeplex青蛙的个数(即可行解的个数)，则初始解(青蛙种群)的个数为：Npop=Nm×Nf。

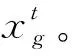
3)青蛙分配：将排好序的青蛙依次循环分配到Nm个子群(即第1只青蛙到第1个子群，第Nm个青蛙到最后一个子群，第Nm+1只青蛙又到第1个子群，周而复始，直到所有青蛙分配完毕)。

4)确定局部搜索(Memetic 进化)迭代次数为Iter。

5)Memetic 进化：

②更新操作

式中：Fitness函数为适应度函数，Δxwmax表示蛙跳最大步长。rand()为(0,1)的随机数。

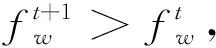
④t=t+1，ift≤Iter，转到①。

6)洗牌(种群信息交换)：

2.1.2 改进的蛙跳算法

1)新的最差青蛙跳跃策略。

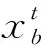
(2)

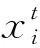
2)加入自适应跳跃因子。

式(2)中rand()函数起到更新步长的作用。但由于rand()函数是一个随机数，很不稳定，会引起步长更新过大或步长更新过小，这样就导致了在最优解附近不停地搜索或者算法收敛时间较长。

数值实验表明，蛙跳算法的跳跃距离应该在开始时大些，保证在整个解空间中搜索，到了后期应该取较小值，以便算法尽快收敛。根据跳跃距离先大后小的特点，本文设计了一种自适应跳跃算子，使得跳跃距离根据算法的运算过程自适应地调整。自适应跳跃因子为

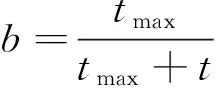
式中：tmax为进化的最大代数，t为当前进化代数。c为系数，取值范围为[0.2,0.6]。则式(2)可修改为

2.2 LRQ控制器的参数优化

本文将采用改进蛙跳算法对 LQR 控制器设计中的权值Q1,1和Q3,3进行多目标优化。

具体算法流程图如图2。

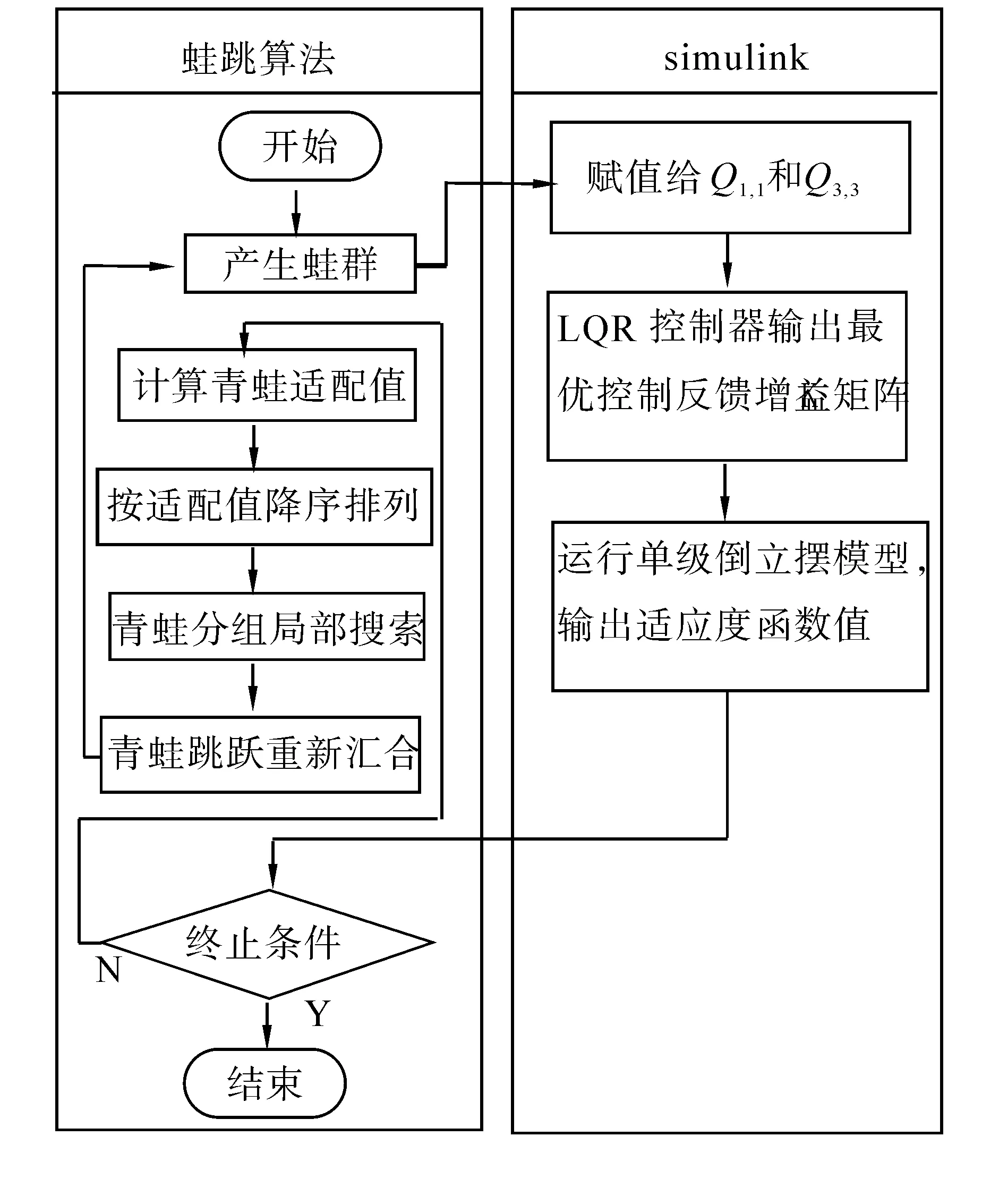
图2 蛙跳算法优化LQR过程示意图Fig.2 The optimization LQR process of SFLA

图2中，改进蛙跳算法与Simulink模型之间连接的桥梁是最优蛙(既LQR控制器参数)和该青蛙对应的适配值(既控制系统的性能指标)。优化过程如下：改进蛙跳算法产生蛙群(可以是初始化蛙群，也可以是更新后的蛙群)，将蛙群中的青蛙依次赋值给LQR控制器的参数Q1,1和Q3,3，然后运行控制系统Simulink模型，得到该组参数对应的性能指标，该性能指标传递到蛙跳算法中作为该青蛙的适配值，最后判断是否退出算法。

3 实验结果与分析

对于LQR控制器参数优化问题已经有多种方法，本文采用标准蛙跳算法、改进蛙跳算法、粒子群算法、遗传算法共4种方法对LQR控制器的参数进行优化，寻找出合适的Q1,1和Q3,3。各算法参数设置如下：

1)遗传算法：采用文献[8]的参数集，种群规模为100，变异概率为0.05，交叉概率为0.3。

2)粒子群算法：利用文献[9]的建议，种群规模为100，认知学习因子为2.9、社会学习因子为1.2、惯性因子为0.4。

3)标准蛙跳算法和改进蛙跳算法：采用文献[10]的建议，文化基因体数为20，文化基因体中青蛙数为10，独立进化次数为10，个体最大进化步长Smax=100%变化范围。

迭代次数改进蛙跳算法设置为50，其他3种均设置为100。

对这4种算法优化同一模型的结果进行比较，以此来检验改进蛙跳算法对此类问题的优化性能。实验结果如图3和图4，仿真得出，遗传算法(GA)的稳态误差为0.24%，而粒子群算法(PSO)、标准蛙跳算法(SFA)、改进蛙跳算法(ISFA)求解后没有稳态误差。

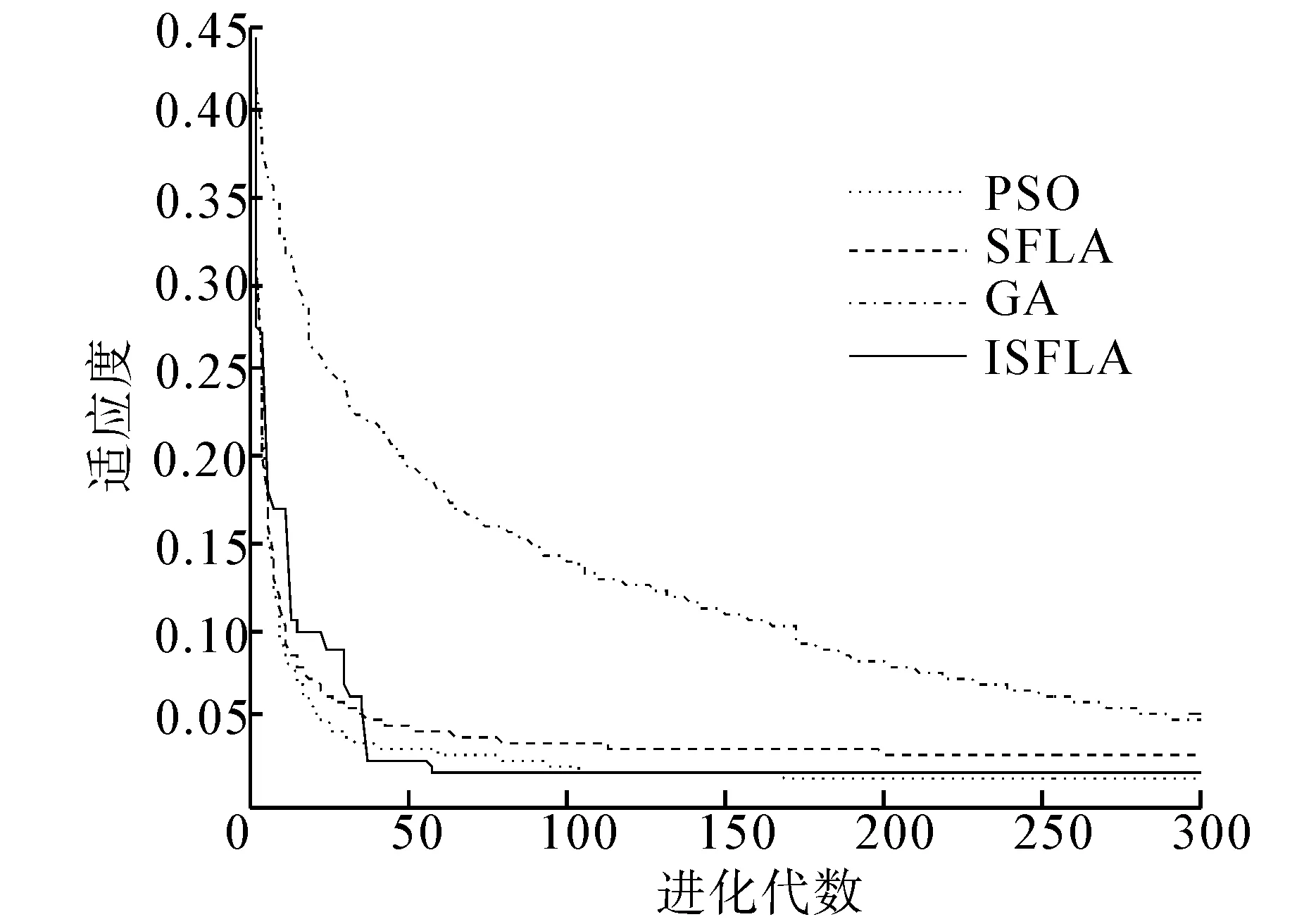
图3 改进蛙跳算法适应度变化曲线Fig.3 Improved shuffled frog-leaping algorithm fitness curve

从图3可以看出改进蛙跳算法在进化代数为58.2时，最优解就稳定下来，粒子群算法、标准蛙跳算法在120代之后最优解才稳定下来，而标准的遗传算法在接近300代时仍然未稳定下来，说明最优解还有上升的可能，由此可见，改进蛙跳算法在快速收敛性方面有较好表现。

针对单级倒立摆的控制，实验系统的模型参数如下:

小车质量M为1.075 kg ，摆杆质量m为0.105 kg ，摆杆长度l为0.25 m ， 小车摩擦系数μ为0.1 N/m/sec ，摆杆转动惯量I为0.003 5 kg·m2。根据不同算法得到的Q1,1和Q3,3代入单级倒立摆模型得到的摆角响应曲线如图4所示。

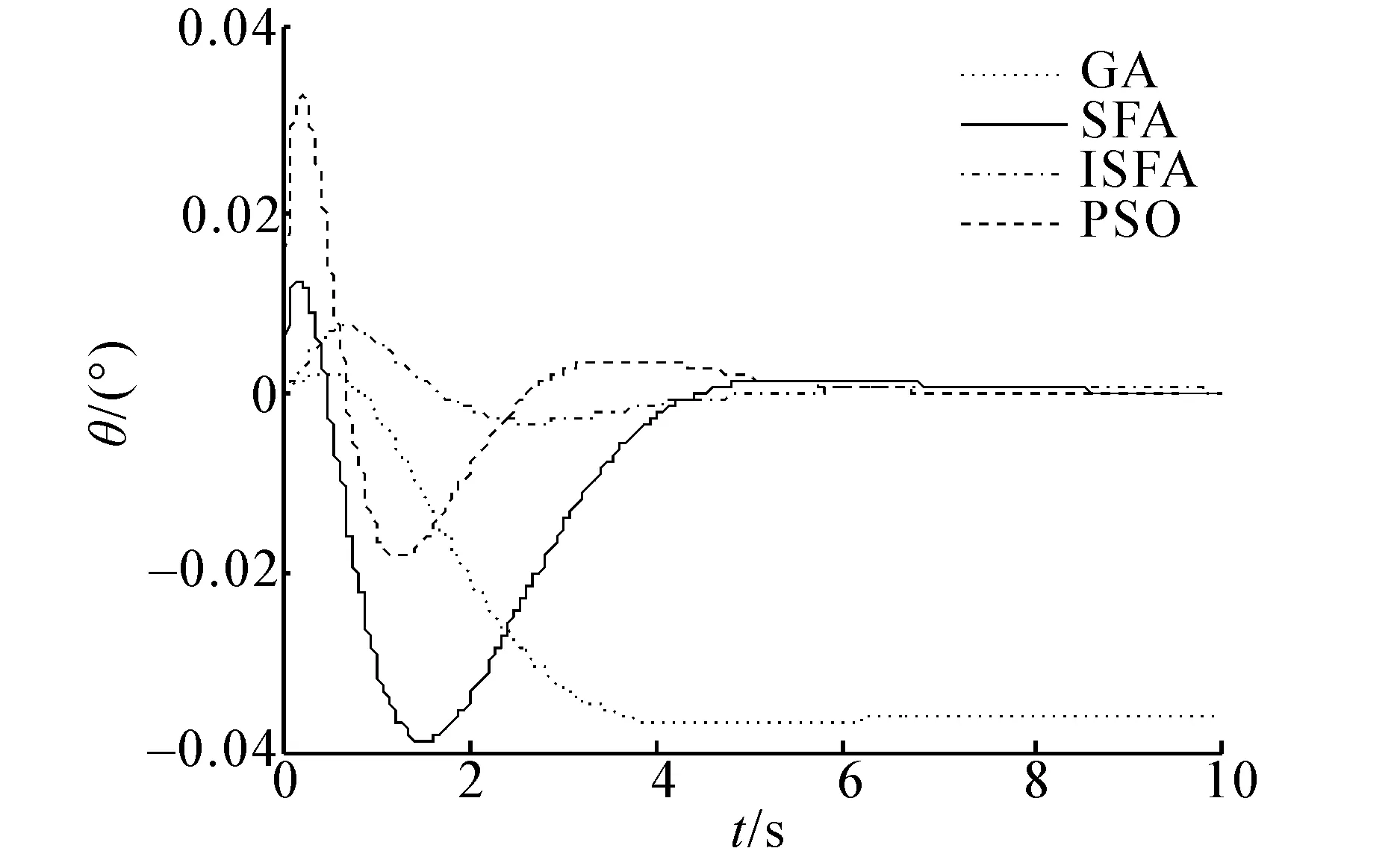
图4 不同算法得到的摆角响应曲线Fig.4 The comparison of response curve

从图4可以看出，系统能较好地跟踪阶跃信号，改进蛙跳算法对LQR控制器参数优化的效果最好，超调量、稳态误差等都有较好的表现，其中超调量是控制系统在阶跃信号输入下的阶跃响应曲线分析动态性能的一个指标值，表示被调参数动态偏离给定值的最大程度；稳态误差是指当系统从一个稳态过度到新的稳态，或系统受扰动作用又重新平衡后，系统可能会出现偏差，这种偏差称为稳态误差，改进蛙跳算法在LQR参数优化上有较好的寻优能力，所得参数对一级倒立摆的控制效果很好，精度也很高。

4 结束语

本文标准蛙跳算法的基础上，通过改进跳跃策略和增加自适应因子等方法，设计了一个新的蛙跳算法的来对LQR控制器进行优化设计，该算法相比于进化算法在收敛性和控制精度上有显著提高，可以较广泛的用于工业控制领域，后续工作主要是继续研究改进蛙跳算法对PID控制器的参数的调整，以期适应更广泛的控制领域。

参考文献:

[1]刘浩梅,张昌凡. 基于LQR的环形单级倒立摆稳定控制及实现[J]. 中南大学学报：自然科学版,2012,43(9): 3496-3501.

LIU Haomei, ZHANG Changfan. Stability control and realization of single link rotary inverted pendulum on LQR controller[J]. Journal of Central South University： Science and Technology, 2012, 43(9): 3496-3501.

[2]张白莉. 单级倒立摆控制系统的稳定性算法设计[J]. 现代电子技术, 2011, 34(3): 120-122.

ZHANG Baili. Stability algorithm design of first-order inverted pendulum control system[J]. Modern Electronics Technique, 2011, 34(3): 120-122.

[3]XU X. Suboptimal LQR problem: controller uncertainty and static output feedback controller[C]//Proceedings of the 23nd Chinese Control Conference. Changsha， China， 2004： 25-32.

[4]胡蓉,陶雪华.单级倒立摆的LQR控制和DMC控制Matlab仿真比较[J].工业控制计算机, 2011, 26(8): 38-40.

HU Rong, TAO Xuehua. Comparison study of LQR control and DMC control on single inverted pendulum[J]. Industrial Control Computer, 2011, 26(8): 38-40.

[5]ALIREZA R V. A hybrid multi-objective shuffled frog-leaping algorithm for a mixed-model assembly line sequencing problem[J]. Computers and Industrial Engineering, 2007, 53(9): 642-666 .

[6]贺毅朝,曲文龙,许冀伟. 一种改进的混合蛙跳算法及其收敛性分析[J]. 计算机工程与应用, 2011, 47(22): 37-40.

HE Yichao,QU Wenlong, XU Jiwei. Improved shuffled frog-leaping algorithm and its convergent analysis[J]. Computer Engineering and Applications, 2011, 47(22): 37-40.

[7]LI Yinghai, ZHOU Jianzhong, ZHANG Yongchuan, et al. Novel multi-objective shuffled frog leaping algorithm with application to reservoir flood control operation[J]. Journal of Water Resources Planning and Management, 2010, 136 (4): 217-226 .

[8]张倩,杨耀权. 基于遗传算法的PID控制器参数优化方法研究[J].电力科学与工程, 2011, 27(11): 53-57.

ZHANG Qian, YANG Yaoquan. PID controller parameters optimization method based on genetic algorithm[J]. Electric Power Science and Engineering, 2011, 27(11): 53-57.

[9]应明峰,鞠全勇,高峰. 基于粒子群优化的PID控制器设计与应用[J].计算机仿真, 2011, 28(11): 283-287.

YING Mingfeng, JU Quanyong, GAO Feng. Design and application of PID controller based on particle swarm optimization[J]. Computer Simulation, 2011, 28(11): 283-287.

[10]葛宇,王学平,梁静.改进的混合蛙跳算法[J].计算机应用, 2012, 32(1): 234-237.

GE Yu, WANG Xueping, LIANG Jing. Improved shuttled frog-leaping algorithm[J]. Journal of Computer Applications, 2012, 32(1): 234-237.