基宽灵敏度分析的径向基神经网络代理模型

张艳霞，陈丹琪，韩莹，刘道华

(1.防灾科技学院 灾害信息工程系,北京 101601； 2. 信阳师范学院 计算机与信息技术学院，河南 信阳 464000)

1 径向基神经网络结构

标准的径向基神经网络模型有3层结构组成，分别为输入层、隐层和输出层，输入层神经元的个数同输入样本点维数相同，即输入层对应着N维输入矢量x=[x1x2…xN]，隐层由K个神经元组成，其与输入层神经元全相连，其是通过隐层的激活函数将线性输入空间映射到非线性隐层空间，每一个隐层神经元的激活函数有高斯型函数、多二次型函数、逆多二次型函数、薄板样条函数组成，常取高斯型基函数[9-12]。

(1)

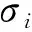
(2)

式中:h=[h1h2…hK]为隐层的输出矢量，wij为隐层的第j个神经元与输出层的第i个神经元的连接权。

2 变基宽灵敏度分析的RBF代理模型

2.1 变基宽的灵敏度分析

(3)

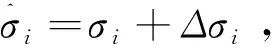
(4)

式中：N是输入样本x的维数，K是隐层神经元基宽数，也是隐层神经元个数。

基于文献[14]提出的计算灵敏度方法，对于第i个神经元在扰动Δx下产生的偏差Si被定义为

(5)

故采用这种扰动递归计算方法，在第K次递归过程中，假设径向基隐层神经元的第K-1个基宽已经被确定，即σi将被确定，因此对于第j个输出神经元的灵敏度被定义为E[(Δyj)2]，即

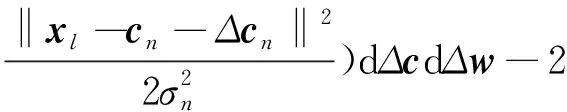
(6)

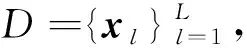
式(6)经展开得

(7)

2.2 基宽灵敏度分析的RBF模型关键参数的获取

由于灵敏度分析能确定径向基关键参数的微小变化对整个径向基构成的影响，但这种分析不能确定RBF模型的具体参数值，故采用灵敏度分析过程中的矩阵信息并应用正交分解方法确定RBF的各具体参数。假设Y=[y1y2…yL]T，L为训练样本数，yi(i=1,2,…,L)表示第i个输出神经元，依据式(2)有

Y=HW=(QA)W

(8)

式中：Y、H、W分别为L×M、L×L、L×M维矩阵，径向基各个隐层神经元基宽的确定可通过矩阵H的关键列分解得到，而H能被分解为QA，其中矩阵Q为L×L维阵并具有正交列[q1q2…qL]，A是一个L×L维上三角阵，具体的H、A阵表示为

在H阵分解过程中，只有一个列能被正交化，且在第K次分解时，一个正交列能够被先前第K-1次正交列得到，具体的相关分解式为

(9)

通过式(9)计算矩阵H的各次迭代的正交列，并能通过RBF灵敏度分析对各正交列进行排序。

假设S(K)(σi)表示为在第K次迭代过程中前K-1个RBF宽度与该σi相关的qi值，且1≤i≤L。并将式(3)以及式(7)中的相关连接权用式(10)代替。

(10)

然后计算径向基神经网络K个隐层各个径向基基宽的灵敏度值，并设Q(K)为第K次迭代的正交矩阵的值，而Q(K)被排序为

‖S(K)(c1)‖≥‖S(K)(c2)‖≥…‖S(K)(cL)‖

(11)

对采用RBF灵敏度分析获得各个基宽的排序值，最终获得RBF的关键基宽，从而获得RBF整个结构的参数值。

2.3 基宽灵敏度分析的RBF代理模型构建算法

通过灵敏度分析及正交变换阵即可获得径向基基宽，即具体代理模型的结构参数，具体算法描述为：

1)通过L个训练样本数据点信息构建3层RBF网络初始结构，并对该网络结构的所有参数进行初始化，包括构建矩阵H、K个隐层节点、每个隐层径向基函数中心、基宽以及隐层与输出层的所有连接权wij的初始化。

2)依据灵敏度分析式(7)计算H中的每一列值，并将该列最大灵敏度值赋给Q(1)，然后计算该训练样本的输出值与样本的期望值的差值E(1)，此时设置K=2。

3)依据式(9)计算正交阵H中的剩余Q(K-1)列。

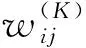
5)判断E(K)-E(K-1)≤δ,δ为事先设定的常数值，如果该式成立，则转7)；否则转6)。

6)计数器K=K+1，并转3)。

7) 输出矩阵Q(K)中的第K列值，即为该径向基函数神经网络的所有隐层神经元的高斯基基宽。

3 实例测试

(12)

式中：fe(x(i))、f(x(i))分别为模型的真实值、代理模型获得的输出值。

F1:f(x,y)=

100≤x,y≤100

F2:f(x,y)=

-3≤x≤3,-2≤y≤2

在实验过程中，采用Intel(R) Core(TM) i3-2120, 3.30GHz CPU，并在MATLAB7.0编程环境下实验，且参数δ=0.45。表1、2为试验对比结果。

表1 训练时间对比

表2 标准差对比

由表1、表2中可知，在相同的训练样本点数时，采用本文方法所需要的训练时间都比采用固定基宽方法需要的时间长，这主要是由于采用该方法时，各个隐层径向基基宽在每一次训练过程中均需要进行灵敏度分析，且需要正交矩阵相关列的计算以及连接权值的调整，但从获得的代理模型精度上来看，不管采用样本数多少，本文所提方法获得模型的标准差均远小于采用固定基宽方法，前者精度比后者精度高一个数量级。从样本点数多少来对比模型的精度，样本点数足够大并不能提高模型精度，也就是训练样本点取合适足够数即可，无需采集大样本数据进行径向基网络的训练，该结果也可从2种模型的对比图(如图1～6所示)反映出，其中图1、2和3分别为函数F1在样本点R为80、200、500情况下获得的模型图，图4、5和6分别为函数F2在样本点R为80、200、500情况下获得的模型图。

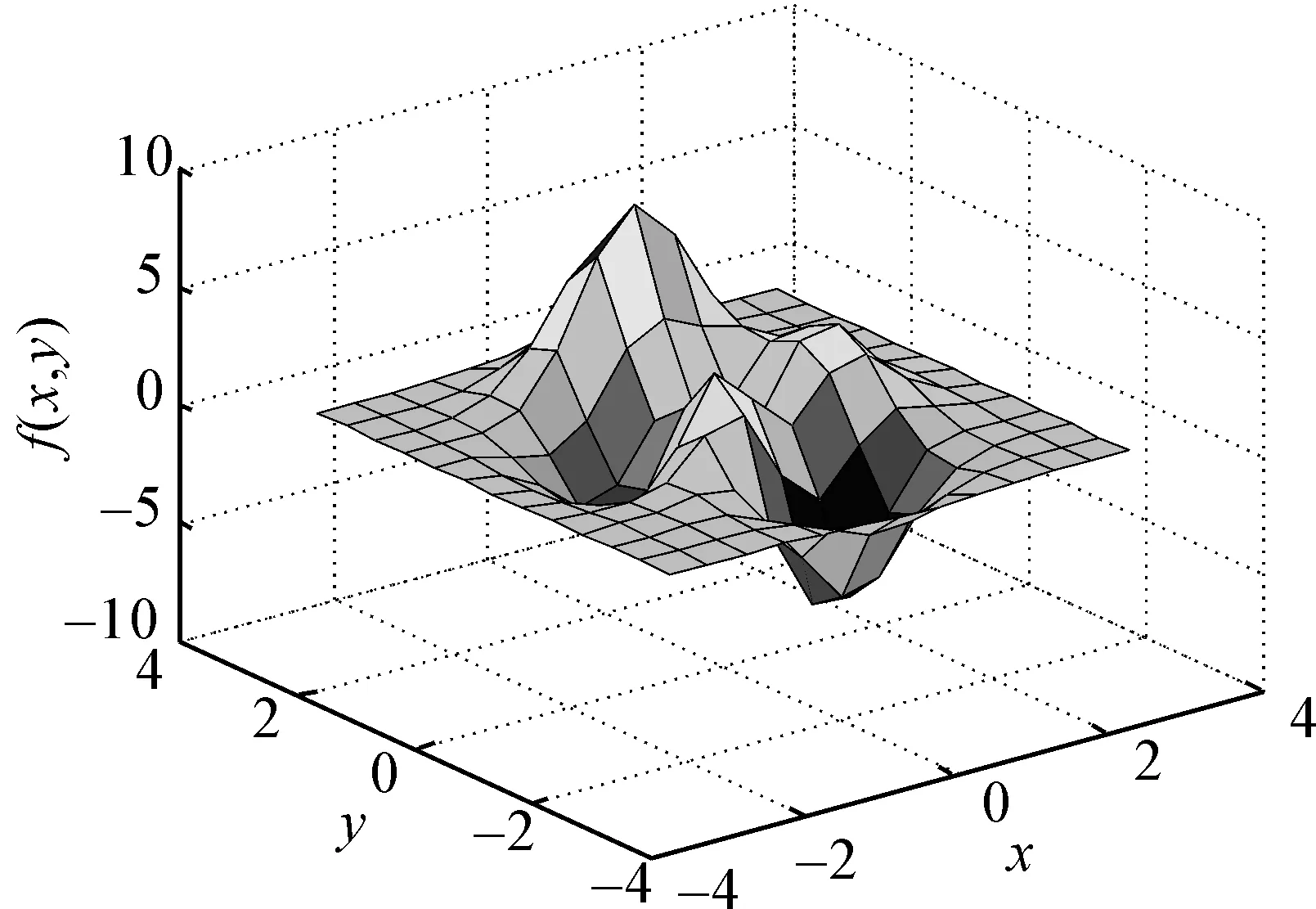
图1 测试函数F1在数据样本点为80时获得的模型Fig.1 The obtained model for the testing function F1(R=80)

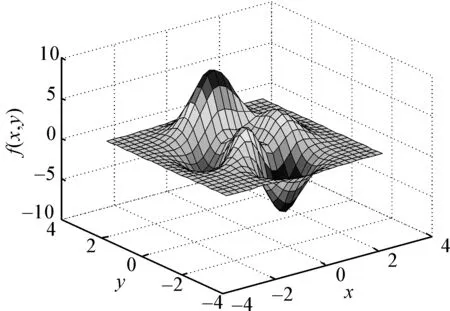
图2 测试函数F1在数据样本点为200时获得的模型Fig.2 The obtained model for the testing function F1(R=200)

图3 测试函数F1在数据样本点为500时获得的模型 图4 测试函数F2在数据样本点为80时获得的模型Fig.3 The obtained model for the testing function F1(R=500) Fig.4 The obtained model for the testing function F2(R=80)

图5 测试函数F2在数据样本点为200时获得的模型 图6 测试函数F2在数据样本点为500时获得的模型Fig.5 The obtained model for the testing function F2(R=200) Fig.6 The obtained model for the testing function F2(R=500)

4 结束语

合适的径向基基宽能提高代理模型的近似精度，本文通过对径向基基宽的灵敏度分析，并对正交矩阵的最大列求解，从而获得隐层各神经元的高斯径向基基宽，最终获得径向基神经网络代理模型结构。采用具体的两测试函数进行验证，证实了这种基宽灵敏度分析的径向基代理模型比采用传统的固定基宽的代理模型具有更高的模型近似精度。同时在实验过程中，也获得采用该方法在构建稳定的代理模型时并不需要太多的训练样本点。为提高代理模型的近似精度，该文只是采用对基宽的灵敏度分析，在以后的工作中有待进一步验证，在基宽灵敏度分析的基础上，同时进行中心灵敏度分析，这样也许能更进一步提高代理模型的精度。

参考文献:

[1]MANOLIS W, NICOLAS T, STEFANOS K. Intelligent initialization of resource allocating RBF networks[J]. Neural Networks, 2005(18): 117-122.

[2]WEI Z, KATIE S, NAN S. Genomic signatures characterize leukocyte infiltration in myositis muscles[J]. BMC Medical Genomics, 2012(5): 1-53.

[3]FRANCESCO P, MASSIMILIANO R, SIMONE R. Numerical and experimental characterization of a novel modular passive micromixer[J]. Biomedical Microdevices, 2012, 14(5): 849-862.

[4]张健，李为吉.飞机多学科设计优化中的近似方法分析[J]. 航空计算技术, 2005, 35(3): 5-8.

ZHANG Jian, LI Weiji. Approximation methods analysis in multidisciplinary design optimization[J]. Aeronautical Computer Technique, 2005, 35(3): 5-8.

[5]赵磊，贾振红，覃锡忠，等. 基于k均值和量子遗传算法的RBF网络优化[J]. 计算机工程, 2011, 37(10): 152-153

ZHAO Lei, JIA Zhenhong, QIN Xizhong, et al. RBF network optimization based on k-means and quantum genetic algorithm[J]. Computer Engineering, 2011, 37(10): 152-153.

[6]李乐庆，康宝生. 基于RBF的散乱点曲面重构[J].西北大学学报, 2011, 41(2): 221-225.

LI Leqing, KANG Baosheng. RBF-based surface reconstruction from scattered data[J]. Journal of Northwest University, 2011, 41(2): 221-225.

[7]MARINARO M, SCARPETTA S. On-line learning in RBF neural networks:a stochastic approach[J]. Neural Networks, 2000(13): 719-729.

[8]张占南. 基于RBF神经网络的γ能谱分析[D]. 大连： 辽宁师范大学， 2011: 43-58.

ZHANG Zhannan. The analysis ofγspectrum by RBF network[D]. Dalian：Liaoning Normal University, 2011: 43-58.

[9]DAVID C, CHEN X W. Radial basis function neural networks for nonlinear fisher discrimination and neyman-pearson classification[J]. Neural Networks, 2003(16): 529-535.

[10]NAM M D, THANH T C. Numerical solution of differential equations using multiquadric radial basis function networks[J]. Neural Networks, 2001(14): 185-199.

[11]刘道华,张礼涛.基于正交最小二乘法的径向基神经网络模型[J].信阳师范学院学报, 2013, 26(3): 428-431.

LIU Daohua,ZHANG Litao. Radial basis function neural network model based on orthogonal least squares[J]. Journal of Xinyang Normal University, 2013, 26(3): 428-431.

[12]KON M A, PLASKOTA L. Information complexity of neural networks[J]. Neural Networks, 2000(13): 365-375.

[13]SHI D, YEUNG D S, GAO J. Sensitivity analysis applied to the construction of radial basis function networks[J]. Neural Networks, 2005(18): 951-957.

[14]ZENG X, YEUNG D S. A quantified sensitivity measure for multilayer perceptron to input perturbation[J]. Neural Computation, 2003(15):183-212.