决策形式背景下的主观贝叶斯概率推理
郑淑贤,解滨,米据生
(1. 河北师范大学 数学与信息科学学院,河北 石家庄 050024; 2. 河北师范大学 信息技术学院,河北 石家庄 050024)
概率推理是根据不确定信息作出推理,同时需要对得出结论的概率作出估计的推理模型。贝叶斯推理问题是条件概率推理问题[1-2],最早在18世纪由英国学者贝叶斯提出,这一领域的研究可以深化人们对概率信息加工过程的理解,能够有效地指导人们进行判断决策以及数据推理。形式概念分析[3]是1982年由Wille首先提出的,它描述了对象和属性之间的联系,在数据分析和知识获取等方面有着非常重要的意义。形式背景是一类具有特殊关系的数据库,其特殊性反映在对象与属性之间的关系仅有是与非2种,决策形式背景是由对象集合、条件属性集合和决策属性集合形成的数据表。
目前许多学者正在进行将贝叶斯概率推理应用到数据库的研究[4-7]。Pawlak[8]建立了贝叶斯理论和数据表之间的联系,Slezak等[9]依据贝叶斯推理提出了贝叶斯数据模型,Y.Y.Yao[10]基于贝叶斯决策过程提出了新的决策理论粗糙集模型,为数据推理提供了新的思想。本文提出的主观贝叶斯概率推理应用了贝叶斯公式的变形公式和主观给出的某些估计量,讨论决策形式背景中条件属性和决策属性的依赖关系。对于决策形式背景,条件属性的重要性存在差异,虽然一些对象含有某种条件属性的数目比较多,但是这些条件属性对决策的影响程度可能比较小;而另外一些对象含有的某种条件属性的数目比较少,但是这些条件属性对决策的影响程度可能比较大。因此,不仅要考虑条件属性的个数,还要考虑条件属性和决策属性的关联程度。
1 基本概念
决策形式背景中知识的发现首先要根据不同的属性将对象进行分类,同一类中的对象均具有共同的属性,所以对属性的研究可以归结到对某类对象的研究。下面给出决策形式背景中对象的分类方法。
定义1[11]称(U,A,I)为形式背景,其中U={x1,x2,...,xn}为对象集,xi(i≤n)称为对象;A={a1,a2,...,am}为属性集,aj(j≤m)称为属性;I为U⊗A上的二元关系,I⊆U⊗A。若(x,a)∈I,则称x具有属性a;若(x,a)∉I,则称x不具有属性a。
定义2[12]如果(U,A,I)与(U,D,J)是2个形式背景,称(U,A,I,D,J)为决策形式背景。
定义3 设(U,A,I,D,J)是一个决策形式背景,当(x,a)∈I时,记为Ia(x)=1,即x具有属性a;当(x,a)∉I时,记为Ia(x)=0,即x不具有属性a。
RA={(xi,xj)∈U×U|Ia(xi)=
Ia(xj),∀a∈A}
称RA为形式背景(U,A,I,D,J)中U上的确定关系。由于关系RA满足自反性、对称性和传递性,因此RA是U上的等价关系。在决策形式背景(U,A,I,D,J)中,由RA可以产生U上的一个划分[13]:
U/RA={[xi]A|xi∈U}
式中:[xi]A={xj∈U|(xi,xj)∈RA}={xj∈
U|Ia(xi)=Ia(xj),∀a∈A}
同样对于决策属性d,有:

2 主观贝叶斯概率推理
概率理论是研究具有不确定性问题的理论,可以将其理解为信任的程度,也就是主观概率。它反映了人们的经验,可能会因人而异。不过它本身的不确定性并不影响其在不确定推理中的应用,依据主观概率进行推理可以更加明显地反映客观事实。下面给出决策形式背景中的主观贝叶斯概率推理。
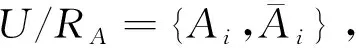
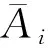
若P是(U,A,I,D,J)上的概率测度,记
∀a∈Ai
则P(Dd/Ai)是条件概率,是集合Ai相对于集合Dd的包含度。
下面根据文献[14],给出决策形式背景中的充分似然率与必然似然率的定义。
定义5 设(U,A,I,D,J)是决策形式背景,其中Ai是条件属性随机变量,Dd是决策属性随机变量,称LS为充分似然率,LN为必然似然率。
(1)
(2)
定理1 设(U,A,I,D,J)是决策形式背景,其中Ai是条件属性随机变量,Dd是决策属性随机变量,则有:
O(Dd/Ai)=LS·O(Dd)
(3)
(4)
式中:
(5)
(6)
(7)
证明由贝叶斯公式可得
(8)
(9)
式(8)、(9)相除即得式(3)。将式(5)和式(6)分别代入式(3),即得
于是
P(Dd/Ai)(1-P(Dd))=LS·P(Dd)(1-
P(Dd/Ai))P(Dd/Ai)[(LS-1)P(Dd)+1]=
LS·P(Dd)
即得式(4),证毕。
定理2 充分似然率LS对P(Dd/Ai)的影响为
1)LS=1时,P(Dd/Ai)=P(Dd),即i-条件属性对决策属性d的可信度无影响;
2)LS>1时,P(Dd/Ai)>P(Dd),即i-条件属性增加决策属性d的可信度;
3)LS<1时,P(Dd/Ai) 证明设y=P(Dd/Ai),a=P(Dd),x=LS,则式(4)成为 y=ax/a(x-1)+1 对x求导即得 若0 例1 一个关于人体健康状况的信息系统如表1,其中U={x1,x2,x3,x4,x5,x6},A={a1,a2,a3},D={d},d成立表示人体健康,d不成立表示人体不健康。 表1 关于人体健康的决策表 定理3 设(U,A,I,D,J)是决策形式背景,其中Ai是条件属性随机变量,Dd是决策属性随机变量,则有 (10) (11) 式中: 证明仿定理1可证。 证明仿定理3.2可证。 主观贝叶斯概率推理为决策形式背景中的条件属性和决策属性间的关系讨论提供了一种简便的方法,计算在一定条件属性下决策成立的可信度,主要根据专家的经验知识给出充分似然率与必然似然率,由式(1)、(2)得 故可得到以下结论: 1)LS=1,当且仅当LN=1; 2)LS≠1(LN≠1),时必有(LS-1)(LN-1)<0; 3)当P(Dd/Ai)=0时,必有P(Ai/Dd)=0,于是LS=0,即对象具有i-条件属性时决策属性d必然不成立; 5)当1 6)当1 由于在主观贝叶斯概率推理中,LS和LN是专家根据经验主观给出的,在给出LS和LN时必须充分理解它们的实际意义,也就是要满足以上6条性质。 2)对于∀ 3)对于 称D为F(X)上的包含度。 容易验证: 是2种不同的包含度。 定理5 设(U,A,I,D,J)是决策形式背景,其中Ai是条件属性随机变量,Dd是决策属性随机变量,则有 证明由定理1和定理2可知: 根据全概率公式: 及 就有 于是得到 同理可得 证毕。 证明由函数的单调性可证。 定理7 设(U,A,I,D,J)是决策形式背景,其中Ai是条件属性随机变量,Dd是决策属性随机变量,以下关系成立: 证明由于 同理可证 证毕。 例2 根据表1,可以得出P(Dd)=2/3, 本文将主观贝叶斯概率推理的方法应用到决策形式背景中,从推理的角度分析了属性值之间的关联性。推理过程接近人们在日常生活中获得概率信息作出判断的情况,清晰地反映出实际应用的信息特点和概率判断的过程,为决策形式背景的数据挖掘和决策判断提供了新的理论依据。在后续的研究中,将进一步探讨基于贝叶斯推理的形式背景中条件属性约简方法。 参考文献: [1]张文修,梁怡,徐萍. 基于包含度的不确定推理[M]. 北京:清华大学出版社, 2007: 107-113. [2]张惠玲,孙剑,邵海鹏. 基于贝叶斯推理的HCM延误模型修正[J]. 计算机工程, 2011, 37(7): 18-20. ZHANG Huiling, SUN Jian, SHAO Haipeng. HCM delay model modification based on Bayesian reasoning[J]. Computer Engineering, 2011, 37(7): 18-20. [3] WILLE R. Restructuring lattice theory: an approach based on hierarchies of concept[M]//Ordered Sets, Reidel, Dordrecht. Boston, USA, 1982: 445-470. [4]ZHANG H Y, ZHOU J, MIAO D Q, et al. Bayesian rough set model: a further investigation[J]. International Journal of Approximate Reasoning, 2012, 53(4): 541-557. [5]YAO J T , YAO Y Y. Probabilistic rough sets: approximations, decision-makings and applications[J]. International Journal of Approximate Reasoning, 2008, 49(3): 253-254. [6]PAWLAK Z. A rough set view on Bayes’ theorem[J]. International Journal of Intelligent Systems, 2003, 18(5): 487-498. [7]SLEZAK D, ZIARKO W. Variable precision Bayesian rough set model[J]. [S.l.]: Springer-Verlag, 2003: 312-315. [8]PAWLAK Z. New look on Bayes’ theorem-the rough set outlook[J]. Rough Set Society, 2001, 5: 20-22. [9]SLEZAK D, ZIARKO W. Bayesian rough set model[C]//International Workshop on Foundation of Data Mining. [S.l.], 2002, 9: 131-135. [10]YAO Y Y. Probabilistic rough set approximations[J]. International Journal of Approximate Reasoning, 2008, 49(2): 255-271. [11]王虹, 张文修.形式概念分析与粗糙集的比较研究[J].计算机工程, 2006, 32(8): 42-44. WANG Hong, ZHANG Wenxiu. Comparative study between formal concept analysis and rough set[J]. Computer Engineering, 2006, 32(8): 42-44. [12]张文修,姚一豫,梁怡.粗糙集与概念格[M]. 西安:西安交通大学出版社,2006: 25-28. [13]米据生,吴伟志,张文修. 基于变精度粗糙集理论的知识约简[J]. 系统工程理论与实践, 2004, 1: 76-82. [14]Nilsson. Artificial intelligence a new synthesis[M].北京: 机械工业出版社, 1999. [15]姚燕青,米据生.直觉模糊集上的混合单调包含度[J]. 计算机科学, 2010, 37(1):255-257. YAO Yanqing, MI Jusheng. Mixed monotone inclusion degree on intuitionistic fuzzy sets[J]. Computer Science, 2010, 37(1): 255-257.
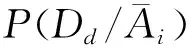

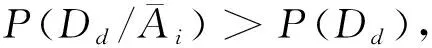

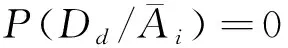
3 基于包含度的概率推理
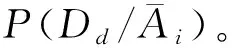

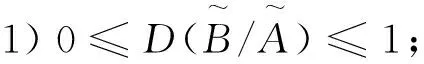
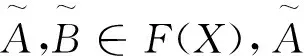


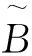
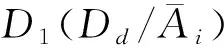

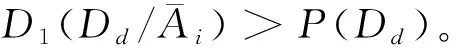

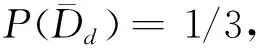

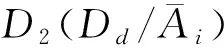
4 结束语

