基于模糊聚类分析的步枪作战效能评估

顾丽娟，李彪，孙慧静，丛萍

（1.海军航空工程学院基础部，山东烟台264001；2.烟台工程职业技术学院管理工程系，山东烟台264001）

基于模糊聚类分析的步枪作战效能评估

顾丽娟1，李彪1，孙慧静1，丛萍2

（1.海军航空工程学院基础部，山东烟台264001；2.烟台工程职业技术学院管理工程系，山东烟台264001）

为了评估步枪的战术效能，科学地构建步枪作战效能评估体系，运用模糊聚类分析方法对步枪作战效能进行评估，最后通过算例验证了所建模型是合理、可行的。

模糊聚类；模糊相似矩阵；作战效能评估；轻武器

轻武器是陆军步兵的基本武器，也是海军、空军及其他军兵种的自卫和近战突击武器，大多由单人或班组操作使用，是当今军事武器库中数量最多、装备最早、用途最广的武器装备。20世纪中叶以后，快速的经济发展和科技的不断进步使得轻武器的发展突飞猛进，步兵轻武器的战斗力也得到了很大的提高，而步枪特别是自动步枪作为轻武器的最主要代表，向着枪族化、猛烈火力、高可靠性、小型化、轻型化等方向发展，其作战效能更是产生了质的飞跃。分析研究国内外轻武器，尤其是对步枪的作战效能指标进行综合评估，对了解军队装备的先进程度，适应新时期军事科学和战备发展具有特别重要的意义。

目前，常用的武器作战效能评估方法主要包括层次分析法和模糊综合评判法[1-3]，即人为给定各个指标不同的权重，最后得到一个量化结果。显然，计算结果不可避免地受到主观因素的影响。为了提高评估的客观性，本文采用模糊聚类分析方法对步枪作战效能进行评估，进而达到将参评步枪科学分组和排序的目的。

1 模糊聚类分析方法

聚类分析是将事物根据一定的特征，并按某种特定要求或规律分类的方法。现实的分类问题往往带有模糊性和复杂性。对带有模糊特征的事物进行聚类分析，分类过程中不是仅仅考虑事物之间有无关系，而是考虑事物之间关系的亲疏程度。对于这类事物的分类，一般用模糊数学方法。通常把应用模糊数学方法进行的聚类分析，称为模糊聚类分析。模糊聚类分析的基本步骤如下。

1）根据不同指标类型，求得规范化数据矩阵[4]。

通常情况下，武器作战效能的各项指标可以定量的分为3种不同类型：第一类指标，要求指标值越大越好，这类指标称为效益型指标；第二类指标，要求指标值越小越好，这类指标称为成本型指标；第三类指标，既非效益型又非成本型，要求指标值越接近该区间越好，这类指标称为区间型指标。本文根据具体的指标类型将原始数据进行规范化处理。

设待聚类的m个样本组成样本集X={x1,x2,…,xm}，每个样本有n项聚类指标，第i个样本的第j项聚类指标为xij(i=1,2,…,m;j=1,2,…,n)。得到m个样本的原始数据X=(xij)m×n(i=1,2,…,m;j=1,2,…,n)。设是原始数据矩阵第j列中的最大值，是原始数

据第j列中的最小值。

若j为效益型指标，则

若j为成本型指标，则

若j为区间型指标，设给定的最优属性区间为为无法容忍下限，x″为无法容忍上限，则j

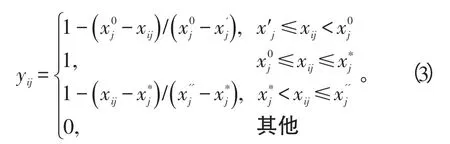
变换后的指标值yij与原指标值xij之间的函数图形为一般梯形。当指标值最优区间的上下限相等，最优区间退化为一个点时，函数图形退化为三角形。

2）建立模糊相似矩阵[5]。建立模糊相似矩阵表示2个样本xi和xj之间的相似程度，rij的计算方法有很多种，如数量积法，相关系数法，最大最小法，算数平均最小法等，可以根据实际需要选用，本文采用最大最小法：

3）构造模糊等价矩阵[6]。

从模糊相似矩阵R=(rij)m×m出发，可以利用传递闭包的方法，来构造一个模糊等价矩阵。为了节省计算量，由平方法有

经过有限次的运算后，一定有R2k

=R2k+1。于是，可以得到一个模糊等价矩阵t(R)=R2k。

4）模糊聚类。

2 步枪的作战效能评估体系的构建

如何更好地分析步枪的作战效能涉及到很多限制条件和不确定因素。本文在参考文献[7-9]和充分考虑多位专家经验的基础上，深入分析影响步枪的作战效能的各种因素，从步枪的战术指标和技术指标中共选取8项作为聚类指标，构建了步枪的作战效能评估体系。具体指标为：射弹初速、有效射程、表尺射程、战斗射速、枪全长、枪全重、弹匣容量。

3 实例分析

选取美国、前苏联和俄罗斯，以及中国的两代自动步枪和突击步枪作为样本，由文献[10]可得拟进行比较的10种步枪的作战效能原始数据如表1所示。我们应用模糊聚类分析的方法对其作战效能进行分类和排序。1）根据不同指标类型，求得规范化数据矩阵。

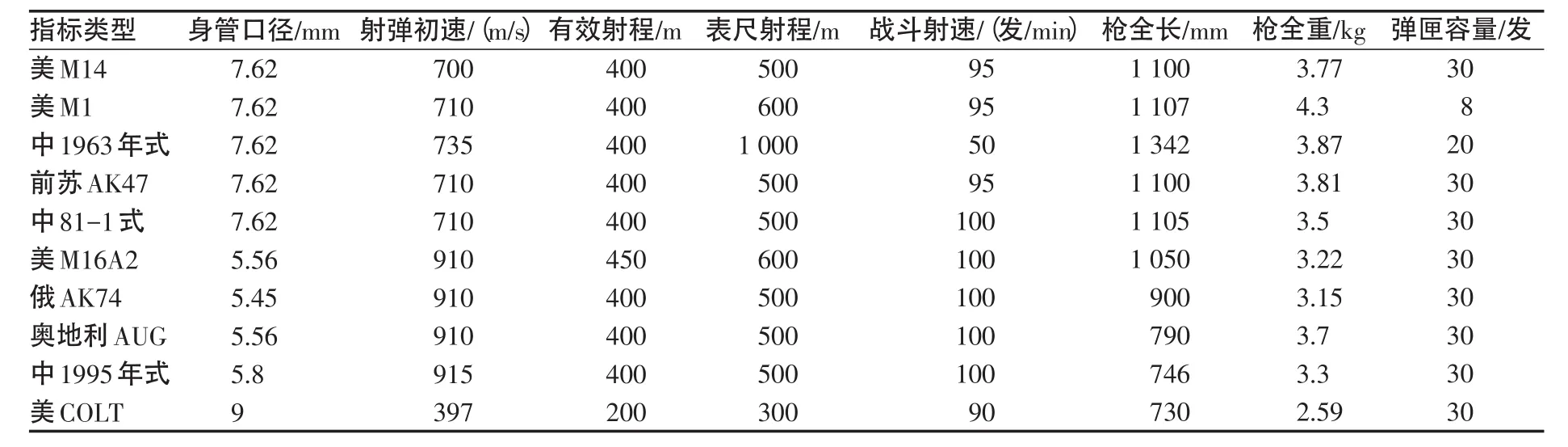
表1 原始数据表Tab.1 Table of primary data

在步枪的作战效能评估体系中，射弹初速、有效射程、表尺射程、战斗射速、弹匣容量为效益型指标；身管口径、枪全重为成本型指标；枪长为区间型指标。根据具体指标类型，选取式（1）、（2）、（6）得到10种步枪的8项指标的规范化数值，如表2所示。

表2 规范化数值Tab.2 Standardized data

续表

2）用最大最小法建立模糊相似矩阵。

根据表2的规范化数据，利用式（4）得到10种步枪的8项评估指标的相似关系矩阵为：

3）构造模糊等价矩阵。

利用式（5），由平方法求得R4=R2∘R2=R2，最终的模糊等价矩阵t(R)为：

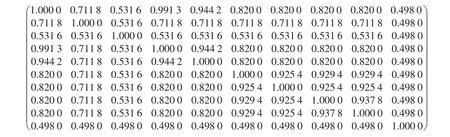
4）模糊聚类。

将t(R)中所有互不相同的元素作为阈值，按从大到小编排如下：

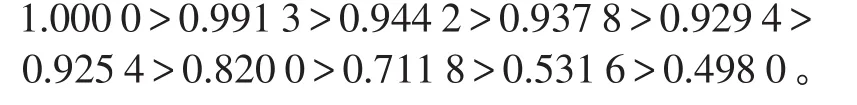
按λ截矩阵t(R)λ进行动态分类：

当λ=1时，X被分为10类，即各个对象自成一类；

当λ=0.991 3时，X被分为9类：{美M14,前苏AK47},{美M1},{中1963年式}, {中81-1式},{美M16A2},{俄AK74},{奥地利AUG}, {中1995年式},{美COLT}；

当λ=0.944 2时，X被分为8类：{美M14,前苏AK47,中81-1式},{美M1},{中1963年式}, {美M16A2},{俄AK74},{奥地利AUG},{中1995年式}, {美COLT}；

当λ=0.937 8时，X被分为7类：{美M14,前苏AK47,中81-1式},{美M1},{中1963年式}, {美M16A2},{俄AK74},{奥地利AUG,中1995年式}, {美COLT}；

当λ=0.9294时，X被分为6类：{美M14,前苏AK47,中81-1式},{美M1},{中1963年式}, {俄AK74},{美M16A2,奥地利AUG,中1995年式}, {美COLT}；

当λ=0.925 4时，X被分为5类：{美M14,前苏AK47,中81-1式},{美M1},{中1963年式}, {美M16A2,俄AK74,奥地利AUG,中1995年式}, {美COLT}；

当λ=0.820 0时，X被分4类：{美M14,前苏AK47,中81-1式,美M16A2,俄AK74,奥地利AUG,中1995年式},{美M1},{中1963年式}, {美COLT}；

当λ=0.711 8时，X被分为3类：{美M14,美M1,前苏AK47,中81-1式,美M16A2,俄AK74,奥地利AUG,中1995年式},{中1963年式}, {美COLT}；

当λ=0.531 6时，X被分为2类：{美M14,美M1,中1963年式,前苏AK47,中81-1式,美M16A2,俄AK74,奥地利AUG,中1995年式}, {美COLT}；

当λ=0.498 0时，X被分为1类，即全部对象成为一类。

根据上述分类结果，得动态聚类图，见图1。

图1 动态聚类图Fig.1 Dynamic clustering graph

4 结语

从上述动态聚类过程可以看出：

1）越先聚为一类的对象，近似程度越高，素质越靠近。体现了“物以类聚，人以群分”的思想。这说明模糊聚类分析方法在评价步枪战术性能中具有较好的效果。

2）同层次分析法和模糊综合评判法比较，模糊聚类分析的方法克服了权重的主观性的弊端，最大限度保证了结果的客观性与科学性。

3）模糊聚类分析是一种探索性分析，分类过程中，给出分类数，但不必事先给出分类标准，这说明模糊聚类分析方法具有较强的可操作性和灵活性。例如，在上述实例分析中，可选取适当的阈值λ=0.925 4，将对象分为5类，可以得到10种步枪作战效能评价的优劣排序：美M16A2、俄AK74、奥地利AUG和中1995式4种步枪作战效能佳，美Ml4、前苏AK47和中81-1式3种步枪作战效能良，美M1、中63式和美COLT步枪作战效能差。

综上所述，模糊聚类方法对步枪作战效能评估具有操作性强、结论科学合理和符合实际的特点，这为步枪的作战使用提供了指导，也为步枪的改进和自主研制、装备保障等提供量化的依据。

[1]林国问，马大为，乐贵高，等.基于FAHP法的多管火箭武器系统效能评估[J].火力与指挥控制，2012，37（9）：98-101. LIN GUOWEN，MA DAWEI，LE GUIGAO，et al.Effectiveness evaluation of MLRS based on FAHP[J].Fire Control&Command Control，2012，37（9）：98-101.（in Chinese）

[2]柯铧，柯科.模糊综合评判在步枪作战效能评估中的应用[J].数学的实践与认识，2011，41（5）：180-185. KE HUA，KE KE.Applications in evaluation of the rifle fighting efficiency by fuzzy synthetical evaluation[J]. Mathematics in Practice and Theory，2011，41（5）：180-185.（in Chinese）

[3]轩永波，黄长强，王勇，等.基于灰色层次分析法的空间武器作战效能评估[J].空军工程大学学报：自然科学版，2011，12（2）：32-37. XUAN YONGBO，HUANG CHANGQIANG，WANG YONG，et al.Effectiveness evaluation of space weapon system based on gray hierarchy method[J].Journal of Air Force Engineering University：Natural Science Edition，2011，12（2）：32-37.（in Chinese）

[4]司守奎，孙玺菁.数学建模算法及其应用[M].北京：国防工业出版社，2011：193-207. SI SOUKUI，SUN XIJING.Mathematical modeling[M]. Beijing：National Defense Industry Press，2011：193-207.（in Chinese）

[5]谢季坚，刘承平.模糊数学方法及其应用[M].2版.武汉：华中科技大学出版社，2005：106-117. XIE JIJIAN，LIU CHENGPING.Applications of fuzzy mathematics[M].2nd ed.Wuhan：Press of Huazhong University of Science and Technology，2005：106-117.（in Chinese）

[6]DUBOIS D，PRADE H.Fuzzy sets and systems：theory and application[M].San Diego：Academic Press，1980：76-90.

[7]YUAN C K，LEE Y H.Effects of rifle weight and handling length on shooting performance[J].Applied Ergonomics，1997，28（2）：121-127.

[8]柯铧，柯科.层次分析法在步枪作战效能评估中的应用[J].数学的实践与认识，2011，41（20）：155-162. KE HUA，KE KE.Applications in evaluation of the rifle fighting efficiency by analytic hierarchy process[J].Mathematics in Practice and Theory，2011，41（20）：155-162.（in Chinese）

[9]KUO CHENGLANG YUAN CHENGKANG，LIU BORSHONG，et al.Using human-centered design to improve the assault rifle[J].Applied Ergonomics，2012，43（6）：1002-1007.

[10]景继生.枪·轻武器发展史[M].天津：百花文艺出版社，2008：81-112. JING JISHENG.Guns the development history of light weapons[M].Tianjin：Baihua Literature and Art Publishing House，2008：81-112.（in Chinese）

Evaluation of the Rifle Fighting Efficiency Based on Fuzzy Clustering Analysiss

GU Li-juan1,LI Biao1,SUN Hui-jing1,CONG Ping2

（1.Department of Basic Sciences,NAAU,Yantai Shandong 264001,China；2.Department of Management Engineering,Yantai Engineering&Technology College,Yantai Shandong 264001,China）

For the purpose of evaluating the effectiveness of rifle,firstly the assessment systems of rifle fighting efficiency scientifically was established.Then a new evaluation model for rifle fighting efficiency was presented by the method of fuzzy clustering analysis.Finally,an example of the assessment model was calculated and the result showed that the model was reasonable,feasible and effective.

fuzzy clustering;fuzzy similar matrix;fighting efficiency evaluation;light weapons

E922.1

A

2014-03-20；

2014-04-02

山东省高等学校科技计划项目（J11LE12）

顾丽娟（1978-），女，讲师，硕士。

1673-1522（2014）03-0280-05

10.7682/j.issn.1673-1522.2014.03.017