能源混沌系统的主动滑模同步控制
徐瑞萍,刘振
1.青岛大学数学科学学院,山东青岛 266071
2.中国海洋大学数学科学学院,山东青岛 266100
◎工程与应用◎
能源混沌系统的主动滑模同步控制
徐瑞萍1,刘振2
1.青岛大学数学科学学院,山东青岛 266071
2.中国海洋大学数学科学学院,山东青岛 266100
研究了一类能源混沌系统的同步问题。基于主动控制理论与滑模控制理论,给出了一种主动滑模控制器的设计方案。由于闭环误差系统依赖于控制器的参数,所以可通过调节这些参数使误差系统渐近稳定,从而实现了能源混沌系统的渐近同步。数值仿真结果说明了所设计方法的有效性与可行性。
混沌;同步;能源系统;主动滑模控制
1 引言
近年来,混沌系统的同步得到研究者和技术人员的广泛关注[1-5]。在过去的20年里,人们提出了许多实现混沌系统同步的方法,如反馈方法、自适应方法、主动控制方法、滑模控制方法、主动滑模控制法等[6-10]。混沌同步不但在化学反应、保密通信、生物医学、信息过程[11-12]等领域有很大的应用潜力和发展前景,随着经济的不断发展,能源的供应和需求问题也得到越来越多的关注。由于能源系统在实际应用中潜在的重要性,这类混沌系统的控制和同步已成为混沌理论研究及应用中的热点问题[13-14]。最近,文献[15]提出了一个新的能源需求-供给动力系统,它是一个三维自治系统,具有非常复杂的动力学行为。文献[16]利用线性反馈控制方法实现了这个系统的同步。
众所周知,滑模控制(SMC)是一种特殊的非线性控制技术,也是一种控制非线性动力系统强有力的方法[17],SMC的主要特点是对内部参数的不确定性和外部扰动都具有很强的鲁棒性。主动控制技术可以消除系统的非线性项。本文结合主动控制和滑模控制技术,设计了一种主动滑模控制器,通过选择合适的控制器参数使得误差系统渐近稳定,从而实现能源混沌系统的同步。
2 系统描述
考虑文献[15]提出的能源系统:
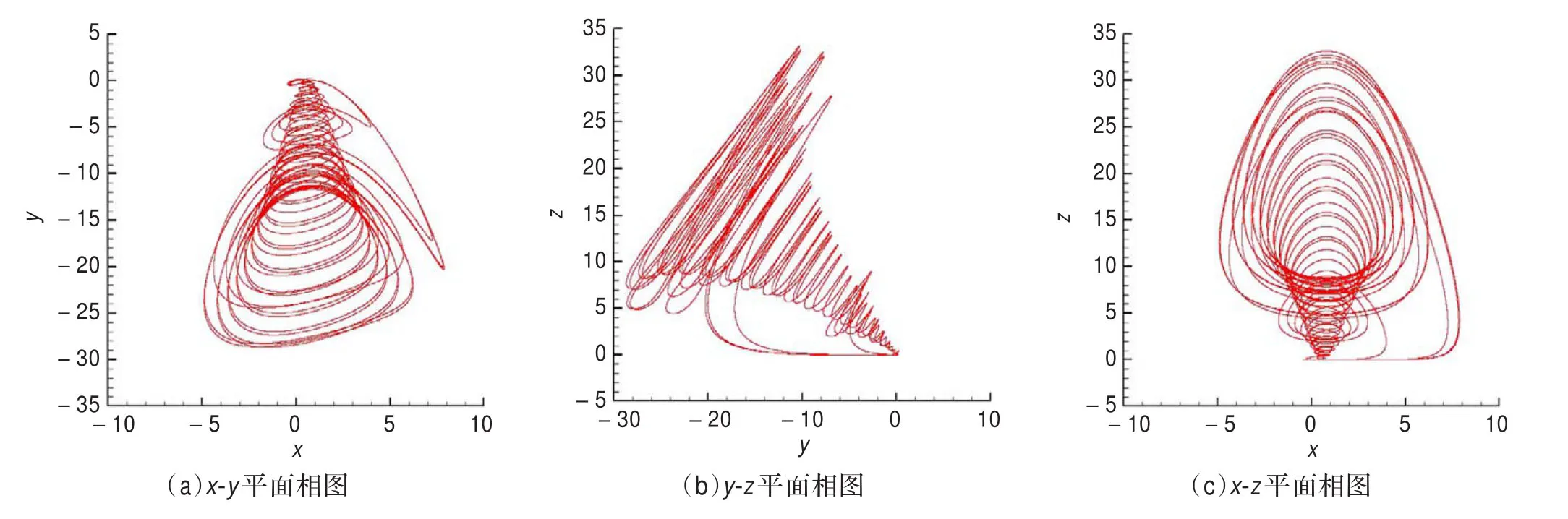
图1 能源系统式(1)的混沌吸引子

3 主动滑模控制器的设计和分析
主动滑模控制器是主动控制器和滑模控制器的结合,下面分别给出它们的设计方法。
3.1 主动控制器的设计
设有驱动系统和响应系统,分别用(x1,y1,z1)和(x2,y2,z2)表示其状态向量。驱动系统的状态方程表示为:
其中a3=a1/M,b4=b3N,d1=c1c3,d2=c1c2。因此,系统式(2)与式(3)的同步问题,转化为系统式(5)的稳定性问题,即
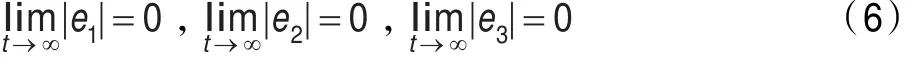
根据主动控制设计程序,选择控制输入u(t)∈R3用来消除误差动力系统式(5)的非线性部分,即选择如下的主动控制函数:
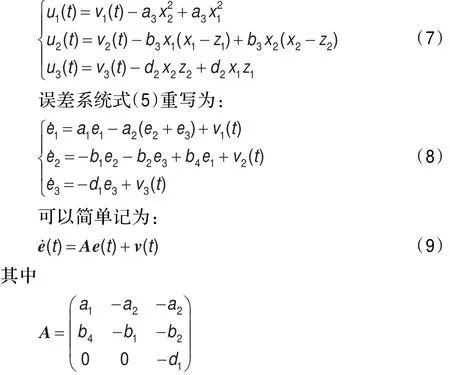
v(t)=(v1(t),v2(t),v3(t))T。方程(9)是带有新控制输入v(t)∈R3的误差系统。关于控制v(t)的选取有许多方法,此处选滑模变结构控制:

其中h=(h1,h2,h3)T是常向量,w(t)∈R是控制输入且满足:

其中s=s(e)是切换函数。将式(10)代入方程(9),可得误差系统:

3.2 滑模面的设计
选取切换面:

基于文献[17]中的等效控制法,在滑模面上应满足:

因此只要选取合适的C,h,使系统式(18)具有负实部的特征根,就能保证滑模运动是渐近稳定的。
3.3 滑模控制器的设计
下面选择合适的控制器使得误差系统的轨线都能在有限时间内到达滑模面。所选控制器应满足到达条件s<0,利用文献[18]中提出的双幂次趋近律:
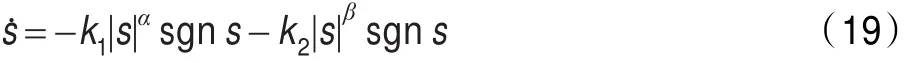
其中sgn(·)表示符号函数,α>1, 0<β<1,k1>0,k2>0是增益。当系统状态远离滑动模态(|s|>1)时,式(19)中第1项起主导作用;当系统状态接近滑动模态(|s|<1)时,第2项起主导作用,两项结合可以保证系统状态在趋近滑动模态过程中的运动品质。
由式(12)和(13)得:

3.4 稳定性分析
定理对于系统式(22),在控制器式(21)的作用下,误差系统是渐近稳定的。即在控制器式(21)的作用下,系统式(2)和系统式(3)达到混沌同步。
证明取Lyapunov函数:

将V沿误差系统式(22)的轨迹对时间t求导,得:
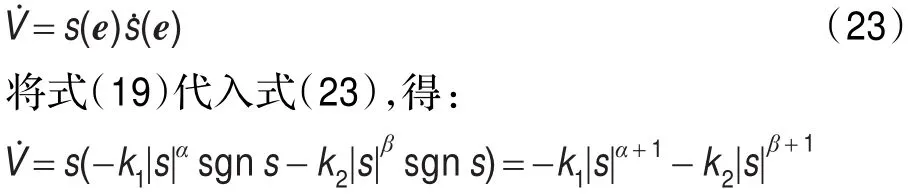
故当k1>0,k2>0时,是负定的,所以误差系统是渐近稳定的。即系统式(2)和系统式(3)达到混沌同步。证毕。
4 数值仿真
利用4阶Runge-Kutta算法进行数值仿真,系统的参数取为a1=0.09,a2=0.15,b1=0.06,b2=0.082,b3=0.07,c1=0.2,c2=0.5,c3=0.4,M=1.8,N=1.0,误差系统的初值取为(-0.5,-1.2,0.4),控制参数取为h=[0.010.40.04]T,C=[1.05-0.281],k1=0.6,k2= 0.2时的数值仿真图(见图2),从图2可以看出,误差系统的状态在t=50之后,就收敛到0。系统切换面s(e)=0运动示意图如图3所示。系统控制器u(t)运动示意图如图4所示。
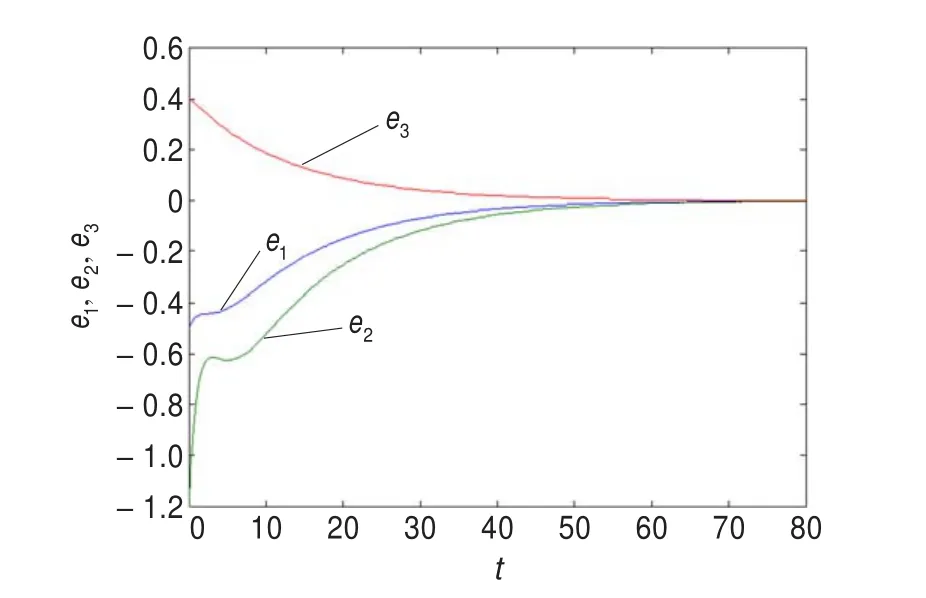
图2 系统误差e(t)=(e1(t),e2(t),e3(t))T运动示意图
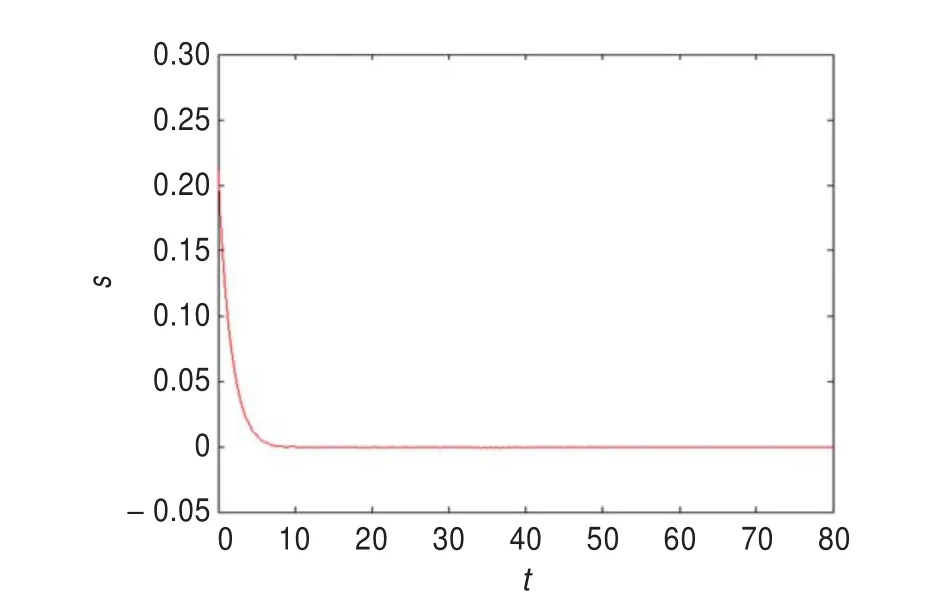
图3 系统切换面s(e)=0运动示意图
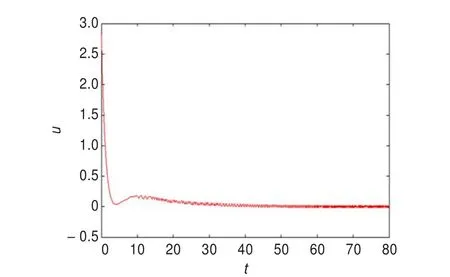
图4 系统控制器u(t)运动示意图
5 结论
本文针对文献[15]提出的能源混沌系统,设计了一种基于双幂次趋近律的主动滑模控制器,通过正确选择控制器的参数使得闭环误差系统渐近稳定,从而能源混沌系统的状态渐近同步。因此,上述方法具有良好的理论研究意义和实际应用价值。
[1]Carroll T L,Pecora L M.Synchronizing chaotic circuits[J]. IEEE Trans on Circ Syst,1991,38:453-456.
[2]Chen G,Dong X.On feedback control of chaotic continuous-time systems[J].IEEE Trans on Circ Syst,1993,40:591-601.
[3]An X L,Yu J N,Li Y Z.Design of a new multistage chaos synchronized system for secure communications and study on noise perturbation[J].Mathematical and Computer Modelling,2011,54:7-18.
[4]Cao J,Li H X.Synchronization criteria of Lur’e systems with time-delay feedback control[J].Chaos,Solitons and Fractals,2005,23:1285-1298.
[5]Ghosh D,Chowdhury A R,Saha P.Synchronization error estimation and controller design for delayed lur’e systems with parameter mismatches[J].IEEE Transactions on Neural Networks and Learning Systems,2012,23(10):1551-1563.
[6]Ma J,Wang Q Y,Jin W Y,et al.Control chaos in the hindmarsh-rose neuron by using intermittent feedback with one variable[J].Chin Phys Lett,2008,25(10):3582-3585.
[7]Sun M,Tian L X,Jiang S,et al.Feedback control and adaptive control of the energy resource chaotic system[J]. Chaos,Solitons and Fractals,2007,32:1725-1734.
[8]张袅娜,周邃,张德江.基于主动控制的异结构混沌系统有限时间同步[J].吉林大学学报,2011,41(4):1131-1134.
[9]Mohammad P A,Sohrab K,Ghassem A.Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique[J].Applied Mathematical Modelling,2011,35:3080-3091.
[10]谭文,蒋逢灵,王耀南,等.一类混沌系统的滑动模态同步控制及其应用[J].计算机工程与应用,2013,49(7):232-234.
[11]张小红,王伟.异维异构混沌系统同步及其在保密通信中的应用[J].计算机科学,2012,39(4):220-222.
[12]Huang C H,Lin C H,Kuo C L.Chaos Synchronizationbased detector for power-quality disturbances classification in a power system[J].IEEE Transactions on Power Delivery,2011,26(2):944-953.
[13]Tian L X,Xu J,Sun M.Chaos synchronization of the energy resource chaotic system with active control[J]. Int J Nonlinear Sci,2006,3(3):228-234.
[14]Sun M,Tian L X,Xu J.Time-delayed feedback control of the energy resource chaotic system[J].Int J Nonlinear Sci,2006,3(3):172-177.
[15]Sun M,Tian L X,Fu Y.An energy resources demandsupply system and its dynamical analysis[J].Chaos,Solitons and Fractals,2007,32:168-180.
[16]Wang Z L.Chaos synchronization of an energy resource system based on linear control[J].Nonlinear Analysis:Real World Applications,2010,11:3336-3343.
[17]高为炳.变结构控制的理论与设计方法[M].北京:科学出版社,1996.
[18]张合新,范金锁,孟飞,等.一种新型滑模控制双幂次趋近律[J].控制与决策,2013,28(2):289-293.
XU Ruiping1,LIU Zhen2
1.College of Mathematics,Qingdao University,Qingdao,Shandong 266071,China
2.School of Mathematical Sciences,Ocean University of China,Qingdao,Shandong 266100,China
Synchronization problem of an energy resource chaos system is investigated.An active sliding mode controller design scheme is proposed via active control theory and sliding mode control theory.The closed loop error dynamic system depends on the parameters of the controller,therefore,the error system achieves asymptotical stability by adjusting these parameters,which means that synchronization of the energy resource chaotic system can be gained.Numerical simulation results are performed to illustrate the effectiveness and feasibility of the proposed control method.
chaos;synchronization;energy resource system;active sliding mode control
A
TP301
10.3778/j.issn.1002-8331.1306-0149
XU Ruiping,LIU Zhen.Synchronization of energy resource chaotic system using active sliding mode controller. Computer Engineering and Applications,2014,50(21):230-233.
徐瑞萍(1976—),女,博士生,讲师,研究方向:混沌系统的控制;刘振(1985—),男,博士生,研究方向:滑模变结构控制。E-mail:xuruiping1228@163.com
2013-06-17
2013-08-02
1002-8331(2014)21-0230-04
CNKI出版日期:2013-11-12,http://www.cnki.net/kcms/detail/11.2127.TP.20131112.1119.015.html

