一种协同的可能性模糊聚类算法

谭欣，徐蔚鸿

长沙理工大学计算机与通信工程学院，长沙 410004

一种协同的可能性模糊聚类算法

谭欣，徐蔚鸿

长沙理工大学计算机与通信工程学院，长沙 410004

模糊C-均值聚类（FCM）对噪声数据敏感和可能性C-均值聚类（PCM）对初始中心非常敏感易导致一致性聚类。协同聚类算法利用不同特征子集之间的协同关系并与其他算法相结合，可提高原有的聚类性能。对此，在可能性C-均值聚类算法（PCM）基础上将其与协同聚类算法相结合，提出一种协同的可能性C-均值模糊聚类算法（C-FCM）。该算法在改进的PCM的基础上，提高了对数据集的聚类效果。在对数据集Wine和Iris进行测试的结果表明，该方法优于PCM算法，说明该算法的有效性。

可能性C-均值聚类（PCM）；模糊C均值（FCM）；协同模糊聚类

1 引言

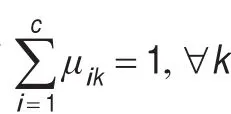
以上聚类算法都是根据数据集的所有特征进行聚类的，每个特征的权值是不同的。若能充分利用特征之间的关系，则聚类的结果会更加精确。协同模糊聚类[15]是一种利用不同特征子集之间的协同关系进行聚类的一种方法。这种方法可与其他的聚类算法相结合，从而提高聚类效果。利用不同特征子集之间的协同系数，得到模糊划分矩阵。优于模糊划分矩阵受不同子集间协同系数的影响，因此要比其他的模糊聚类算法得到的模糊划分矩阵精确、聚类效果好。

本文在上述工作的基础上，对UMPFCA算法进行改进，将协同模糊聚类算法和UMPFCA算法相结合，并将其用于标准数据集的测试，使得聚类性能得到提高。

2 隶属关系不确定的可能性模糊聚类算法

UMPFCA算法将改进的FCM算法与两个新的隶属度参数tik、pik进行融合，其目标函数如下所示：

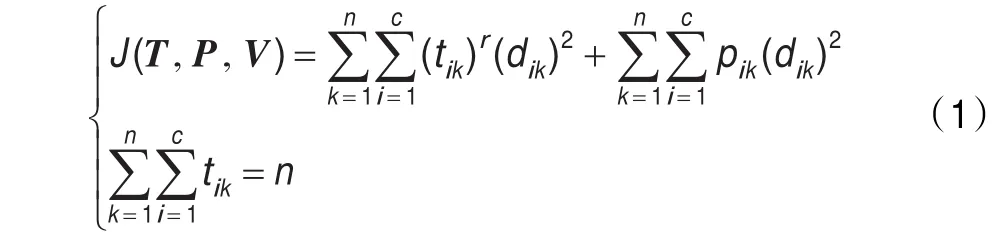
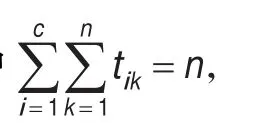
不确定隶属度pik的优点在于有记忆功能，每次迭代中更新数据对象与最近距离聚类间的隶属度值，其他隶属度保持上一次迭代的数值，这样可以“记忆”以前历次迭代过程中的pik，此算法中的不确定性不同于一般概念的不确定性，只有当不同聚类的隶属度都为1时才被定义为不确定性隶属度关系。T，P，V分别为可能隶属度矩阵、不确定性隶属度矩阵及聚类中心矩阵，r为可能性权重指数，r∈(1，∞)。dik表示样本xk与第i类聚类中心Vi之间的欧式距离度量。

根据拉格朗日极值方法求得可能隶属度：

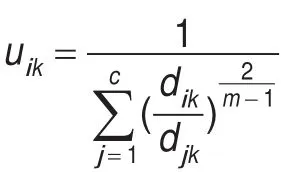
度不会受到其他聚类中心的牵制。

不确定隶属度关系为在聚类算法迭代过程中，当数据集X中第k个数据样本xk对C个聚类中第i个类的隶属度相等的情形，即存在如下情况：

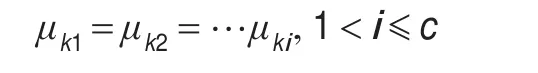
其中，C为聚类个数，表示样本xk对i个聚类ci(1＜i≤c)的隶属关系是不确定的。目前在值域μ上变量取值的分布形式可以分成两种分布情况：概率性分布和可能性分布。在聚类方法中可以分布对应模糊性理论和可能性理论，这两个分布之间有着不同之处，可能性分布取消了概率性分布的约束条件。以上出现的不确定性分布与这两种分布之间有本质区别。不确定模糊聚类算法不同于一般的模糊聚类算法，该算法体现了数据对象对聚类簇隶属关系亦此亦彼的不确定性。

3 协同的可能性模糊聚类算法

协同模糊聚类[14]在普通聚类算法的基础上，将数据的特征分成不同的p个特征子集。每个特征子集的向量个数要相等，并确定不同特征子集之间的协同系数β[ii，kk]，根据协同系数确定不同子集的模糊划分矩阵和原形矩阵。不同特征子集之间的关系强度由协同系数确定，协同系数越大，特征子集之间的协同关系就越强，对模糊划分矩阵和原形矩阵的影响越大；反之，协同系数越小，则相反。

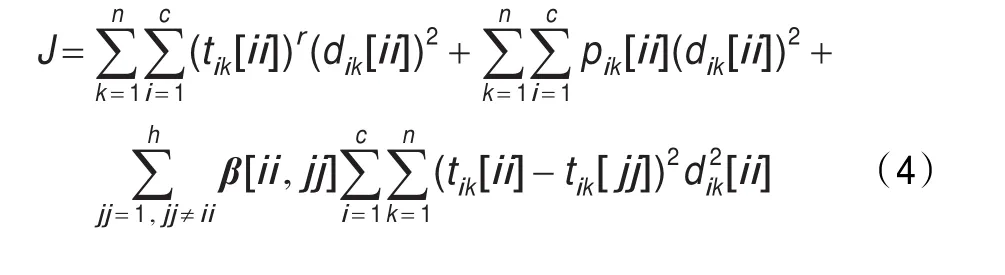
根据此方法，在UMPFCA目标函数的基础上，考虑不同特征子集的模糊划分矩阵之间的协同关系，为此提出如下目标函数：其中，第一部分为UMPFCA目标函数，第二部分是根据各个特征子集的模糊划分矩阵之间的关系而确定。β[ii，jj]是特征子集ii与特征子集jj之间的协同系数矩阵。

根据拉格朗日求极值方法给出vst[ii]的计算公式，首先构造拉格朗日函数V[ii]：

值得注意的是，初始化聚类中心在根据式（6）计算时，需要比随机选取较真实的聚类中心，这样能得到较合理的权值。即先通过FCM得到近似聚类中心，然后使用UMPFCA算法计算其可能隶属度，则得到的以下算法称为C-FCA算法。

C-FCA算法基本分为两个部分：

步骤1初始化过程。对中心矩阵V(0)和可能隶属度矩阵T(0)、非确定性隶属度矩阵P(0)以及一些参数初始化。

步骤2计算中心矩阵V(0)和可能隶属度矩阵T(0)、非确定性隶属度矩阵P(0)。通过内循环和外循环迭代使得两次迭代中心矩阵V(0)差值小于阈值或迭代次数大于TS1，TS2为止。

4 实验结果

为了检验此算法的聚类有效性，使用FCM、WFCM、UMPFCA、C-FCA算法对UCI机器学习库中常被用来检验聚类算法性能的IRIS、Wine数据集进行聚类，用MATLAB7.0编程实现。

IRIS数据是包含3类鸢尾植物Setosa、versicolor、virginica的随机样本，每一类有50个表示IRIS的花瓣长（Petal length）、花瓣宽（Petal width）、萼片长（Sepal length）、萼片宽（Sepal width）的四维空间的样本组成。该数据集的相关资料中的IRIS数据的类中心为(V1= (5.00，3.42，1.46，0.24)，V2=(5.93，2.77，4.26，1.32)，V3= (6.58，2.97，5.55，2.02))。Wine数据集是178个样本构成。

下面用FCM、WFCM、UMPFCA、C-FCA这四种聚类算法对IRIS和Wine数据集进行测试。C-FCA算法中：设置最大迭代次数T1=T2=100，阈值ε=0.01，协同系数β[1.2]=β[2.1]=0.1。IRIS数据集的结果如表1所示。

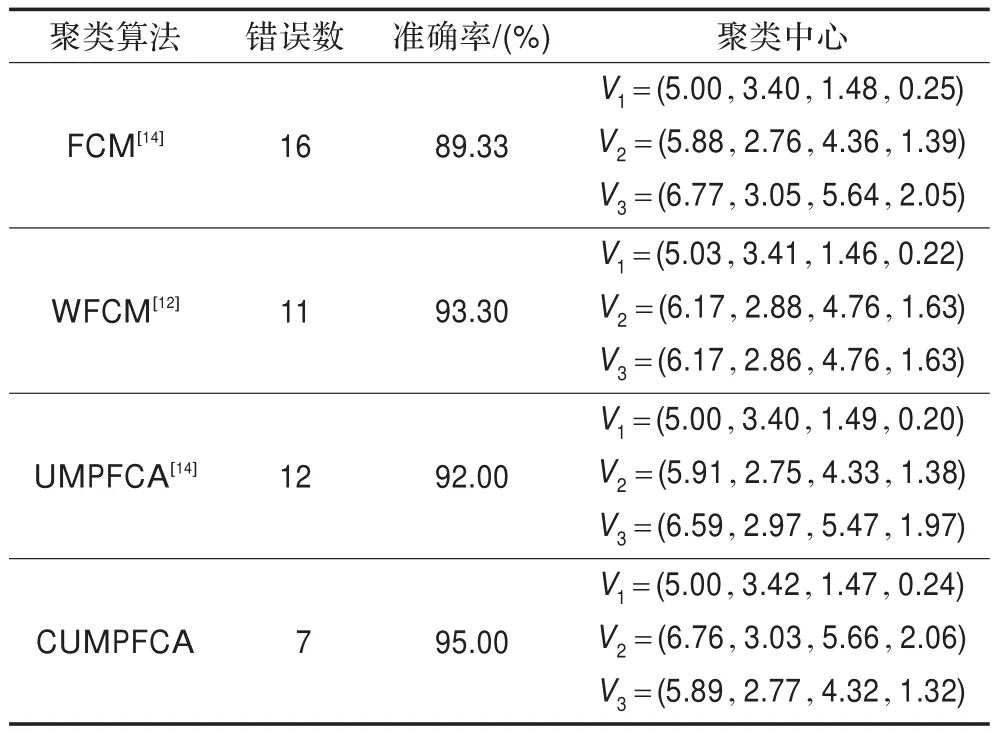
表1 IRIS数据集上四种聚类算法的聚类结果对比1）

在IRIS中，第一类和其他两类完全分离，第二类和第三类有重叠。从表1中可以得到对于IRIS数据，PCM算法最终的误分数仅有10个，但第2个与第3个聚类中心几乎出现了重合，与实际的聚类中心有偏差。UMPFCA有较高的正确率，聚类中心更加接近于真实的聚类中心。C-FCA因为协同系数的影响，得到了较高的准确率。同时C-FCA在聚类结果较好的PCM算法基础上，正确聚类数据进一步提高到96%。表2为FCM、UMPFCA、C-FCA算法对Wine数据集的正确聚类结果。

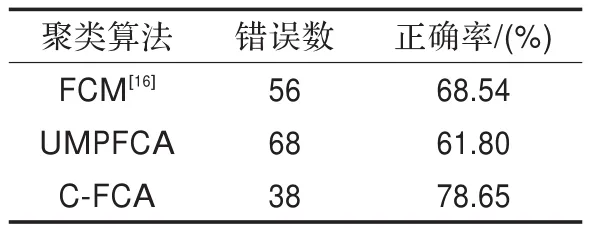
表2 Wine数据集上三种聚类算法的聚类结果对比

可以看出对于Wine数据集，C-FCA正确聚类的数据点数目为140，聚类结果较好，UMPFCA只有110正确聚类结果。C-FCA的正确率达到78.65%。从实验结果可以看到，三种聚类算法中C-FCA聚类算法最好。

二维的IRIS数据集原始分布图如图1所示。

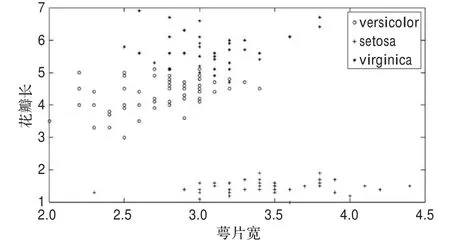
图1 二维的IRIS数据集原始分布图

图2是协同系数β[1，2]=β[2，1]=0.1时的实验结果，协同系数β的取值会影响聚类性能：影响算法的效率。不同值时的结果进行比较如表3，从表中可以看出β取值大于等于0.3时，正确聚类数据的百分比很低。当协同系数取值小于0.08时，聚类结果变动不明显。当取值在[0.08，0.25]区间上，正确聚类数目的百分比为95%，到达最好的聚类结果。

表3 取不同值对IRIS聚类的不同结果比较

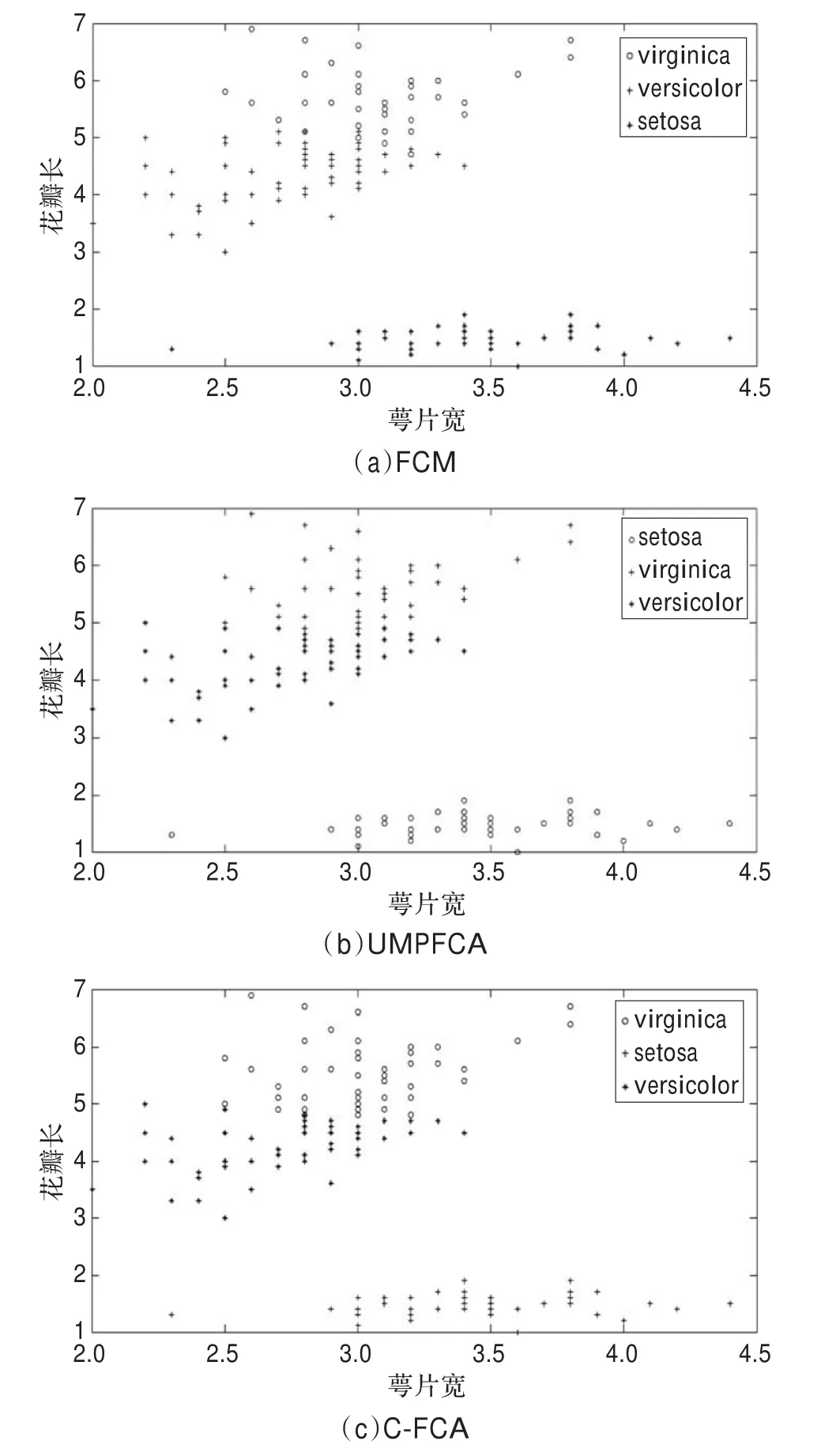
图2 二维的IRIS数据集采用三种算法的聚类效果

在对数据集进行C-FCA算法之前，要先对数据集经过特征选择，IRIS数据集有两个特征子集，分别为2，1，3和2，3，4。经过β取大量的值，当协同系数不断增加时，δ在（0.665，0.669）之间，Δ趋于稳定，所以当协同系数在一定程度上不断增加时，不会影响到δ和Δ，UMFCA和C-FCA算法对IRIS的第二类和第三类的隶属度矩阵的分布情况如图3，图4所示。图4的C-FCA算法得到的同一数据属于两类的隶属度差别更大，较好地描述了聚类的效果。

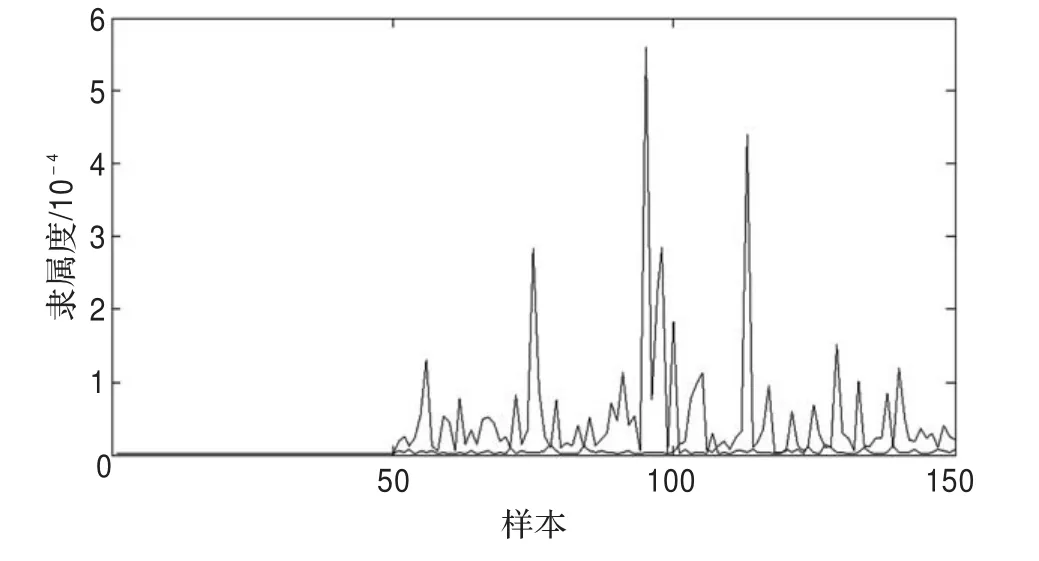
图3 UMPFCA

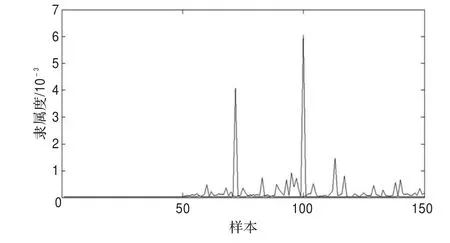
图4 C-FCA

为了验证算法聚类，引入两个准则来对协同系数与隶属度矩阵的关系进行有效性测度。这里引进评估聚类的影响，在后文中对没有任何协同影响作为对比。

在数据集之间，引入数据集1和2协同的影响用两种方式在图中展示，同样的，标记的1-ref和2-ref表示没有任何协同的作用。首先，表达两个划分矩阵的两个特征子集受到协同系数的影响隶属度矩阵的差距，特征子集的划分矩阵分别表示为：U1=[μik[1]]和U2=[μik[2]]。

那么测度函数就是：

显而易见，协同作用越强，即β越大时，δ的值越小，因此，这个参数可以分析协同参数对隶属度的有效影响。协同作用是对称的，β[1，2]=β[2，1]。它反映了数据集被其他模式子集的协同影响。比如，对于数据集结构之间很大不同，那么随着β值的增加δ值就没有变化。

第二个准则是考虑到两个未经过协同计算得到的隶属度矩阵，经过协同聚类计算得到的协同隶属度矩阵和未经过协同计算得到的普通隶属度矩阵的差值与协同系数之间的关系，即

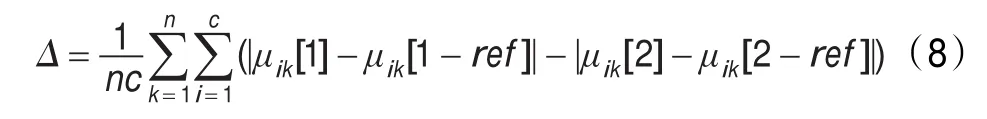
上述的两个测度函数体现了全局特征，那么方便研究单独的特征子集和数据集整体结构。其结果对定义隶属度变化被协同的影响很大而结构在所有数据集中是相容的。

5 结论

本文将UMPFCA算法进行改进，并将其同协同模糊聚类相结合，提出了一种协同的可能性模糊聚类算法（C-FCA）。利用协同模糊聚类在隶属度上的优势和UMPFCA对聚类簇隶属度关系亦此亦彼的不确定上的优势，通过该方法对数据集进行检验，实验结果表明该方法是非常有效的。但本文提出的聚类算法同样存在一些问题，数据量大导致计算量大，费时，协同系数要根据经验确定，且需要大量实验得出合适的值。选择特征子集的参数对数据检验也会影响到最后结果，这些方向的问题有待于进一步的研究。

[1]孙吉贵，刘杰，赵连宇.聚类算法研究[J].软件学报，2008，19（1）：48-61.

[2]Kirindis S，Chatzis V.A robust fuzzy local information c-means clusteringalgorithm[J].IEEE Trans onImage Process，2010，19（5）：1328-1337.

[3]Cai W，Chen S，Zhang D.Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation[J].Pattern Recognition，2007，40（3）：825-838.

[4]张敏，于剑.基于划分的模糊聚类算法[J].软件学报，2004，15（6）.

[5]田军委，黄永宣，于亚琳.基于熵约束的快速FCM聚类多阈值图像分割算法[J].模式识别与人工智能，2008，21（21）：221-226.

[6]Bezdek J C.Pattern recognition with fuzzy objective function algorithms[M].New York：Plenum，1981.

[7]Pal N R，Pal K，Bezdek J C.A new hybrid c-means clustering model[C]//Proc of the IEEE Int Conf on Fuzzy Systems.Piscataway：IEEE Press，2004：179-184.

[8]高新波.模糊聚类分析及其应用[M].西安：西安电子科技大学出版社，2004.

[9]宋鱼庆.医学图像数据挖掘若干技术研究[D].南京：东南大学，2005.

[10]Setnets M.Supervised fuzzy clustering for rule extraction[J].IEEE Trans on Fuzzy Systems，2000，8（4）：416-424.

[11]Krishnapuram R，Keller J M.A possibilistic approach to clustering[J].IEEE Trans on Fuzzy Systems，1993，1（2）：98-110.

[12]刘兵，夏士雄.基于样本加权的可能性模糊聚类算法[J].电子学报，2012，40（2）：371-375.

[13]Pal N R，Pal K，Bezdek J C.A possibilistic fuzzy c-means clusting alogorithm[J].IEEE Trans on Fuzzy Systems，2005，13（4）：517-530.

[14]陈健美，路虎，宋余庆，等.一种隶属关系不确定的可能性模糊聚类方法[J].计算机研究与发展，2008，45（9）：1486-1492.

[15]Pedrycz W.Collaborative fuzzy clustering[J].Pattern Recognition Letters，2002，23（14）：173-186.

[16]祁宏宇，吴小俊，王士同，等.一种协同的FCPM模糊聚类算法[J].模式识别与人工智能，2010，23（1）：120-125.

TAN Xin,XU Weihong

School of Computer&Communication Engineering,Changsha University of Science&Technology,Changsha 410004,China

Fuzzy C-Means（FCM）algorithm is sensitive to noise and Possibilistic C-Means（PCM）algorithm is very sensitive to the initialization of cluster center and generates coincident clusters.With the collaborative relations among different feature subsets,the collaborative fuzzy clustering is combined with other clustering algorithms to make its clustering result better than that of the one with the original algorithm.An improved fuzzy clustering algorithm is proposed based on the combination of PCM and collaborative fuzzy clustering.The experimental results on the data sets show the effectiveness of the proposed method.

Possibilistic C-Means clustering（PCM）;Fuzzy C-Means（FCM）;collaborative fuzzy clustering

A

TP311

10.3778/j.issn.1002-8331.1211-0251

TAN Xin,XU Weihong.Collaborative PCM fuzzy clustering algorithm.Computer Engineering and Applications, 2014,50（21）：147-151.

国家教育部重点科研项目（No.208098）；湖南省科技计划项目（No.2012FJ3005）。

谭欣（1988—），女，硕士研究生，主要研究方向：人工智能与图像处理；徐蔚鸿（1963—），男，教授，博士生导师，主要研究方向：模式识别，人工智能，图像处理。E-mail：tanxincl@163.com

2012-11-21

2013-02-25

1002-8331（2014）21-0147-05

CNKI出版日期：2013-05-13，http://www.cnki.net/kcms/detail/11.2127.TP.20130513.1601.006.html