多阶段双层目标分配问题的精确算法
马芹芹,郭强,付晓薇
西北工业大学理学院,西安 710129
多阶段双层目标分配问题的精确算法
马芹芹,郭强,付晓薇
西北工业大学理学院,西安 710129
针对所有工作必须分阶段依次完成,但同一个阶段的工作可以同时进行的情况下,如何分配现有人员来承担这些工作,才能使得完成所有工作的工期最短,并在此前提下使花费的总用时最少的分配问题,通过引入立方检测矩阵,给出了一种单调下降的迭代算法。该算法不但能获取精确最优解,而且有很好的计算效率。
分配问题;双层目标;立方检测矩阵;迭代算法;精确最优解
1 引言
分配问题通常都与经济效益和社会效益密切相关,而且类型很多[1]。针对以总用时最少为目标的分配问题,文献[2-3]分别给出了求解一对一分配问题的匈牙利法[2]和矩阵迭代法[3];文献[4]给出了求解一对多确定型分配问题的算法;文献[5]给出了求解一对多非确定型分配问题的矩阵迭代法。针对以工期最短为目标的分配问题,文献[6]给出了求解一对一分配问题的O.Gross算法;文献[7]给出了求解一对多确定型分配问题的定界迭代算法;文献[8]给出了求解一对多非确定型分配问题的字典式搜索法。然而,工期最短的分配方案通常并不唯一,因此,可以在获取工期最短的前提下,进一步使总用时最少,其现实意义在于追求最高效率的前提下,最大限度地降低劳动强度。针对这类双层目标分配问题,文献[9]中给出了工作间存在紧前、紧后关系的一对一分配问题的迭代算法;文献[10]给出了求解一对多确定型分配问题的暂态混沌神经网络算法;文献[11]给出了求解一对多非确定型调度问题的多项式时间算法。
上述文献(文献[9]除外)研究的都是所有工作同时进行的情况,然而现实中还存在一些多阶段分配问题,即所有的n项工作必须分m(1<m<n)个阶段依次完成,而同一阶段的工作可以同时进行。该问题同样在现实中有着重要的应用背景。Punnen和Aneja[12]给出了求解以总用时和工期为目标的一对一多阶段分配问题的启发式算法,获取近似最优解。Seshan[13]给出了求解以工期为目标的一对一多阶段分配问题的分枝定界算法,虽然能得到精确解,但计算量太大,效率不高。Sonia和Puri[14]给出了求解m=2时以工期最短为目标的一对一多阶段分配问题的多项式有界算法,但该算法不易推广到2<m<n的情况。Aggarwal等人[15]给出了求解以工期最短为目标的一对多确定型的多阶段分配问题有效算法。目前关于该类问题的双层目标规划的文献还比较少。因此,本文主要针对一对一多阶段双层目标分配问题进行研究,通过借鉴文献[3]的算法思想,给出了可用于迭代运算获取精确最优解的立方检测矩阵,由此形成的算法能保证工期随迭代运算单调递减或者工期不变,但总用时随迭代运算单调递减。
2 多阶段双层目标分配问题的模型分析和相关定义
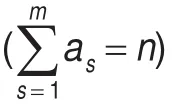

其中外层目标函数式(1)是求在工期最短的前提下使总用时最少,内层目标函数式(2)是求工期最短,内层规划的约束条件式(3)表示每项工作只能由一个人承担,约束条件式(4)表示每个人只能承担一项工作。约束条件式(5)是指xij为0-1变量。
该模型是一个双层0-1整数规划,其可行分配方案的个数为n !,在n较大时,用穷举法求解显然不现实。为此,希望构建一种能够通过迭代运算获取这种多阶段双层目标分配问题的精确最优解的算法。为实现这一目的,需先引入以下概念:

虽然,在i≠j的情况下,立方检测矩阵(dij)n×n中的向量dij并不是(P)的可行分配方案,但是仿照Floyd算法[3]的迭代次序对立方检测矩阵进行迭代,得到的dii(i=1,2,…,n)一定是(P)的可行分配方案。
3 多阶段双层目标分配问题的算法
3.1 算法步骤
根据立方检测矩阵的特点,可以按照下列方法构建多阶段双层目标分配问题的求解思路:首先用最小元素法[16]获取一个可行分配方案,构造当前可行分配方案下的立方检测矩阵,然后按照Floyd算法的迭代次序对立方检测矩阵实施迭代运算,以获取一个工期更短或工期不变,但总用时更少的可行分配方案,不断重复这样的过程,直到最终获得工期最短,并在此前提下总用时最少的可行分配方案,这样的分配方案便是最优分配方案。具体的算法步骤如下:

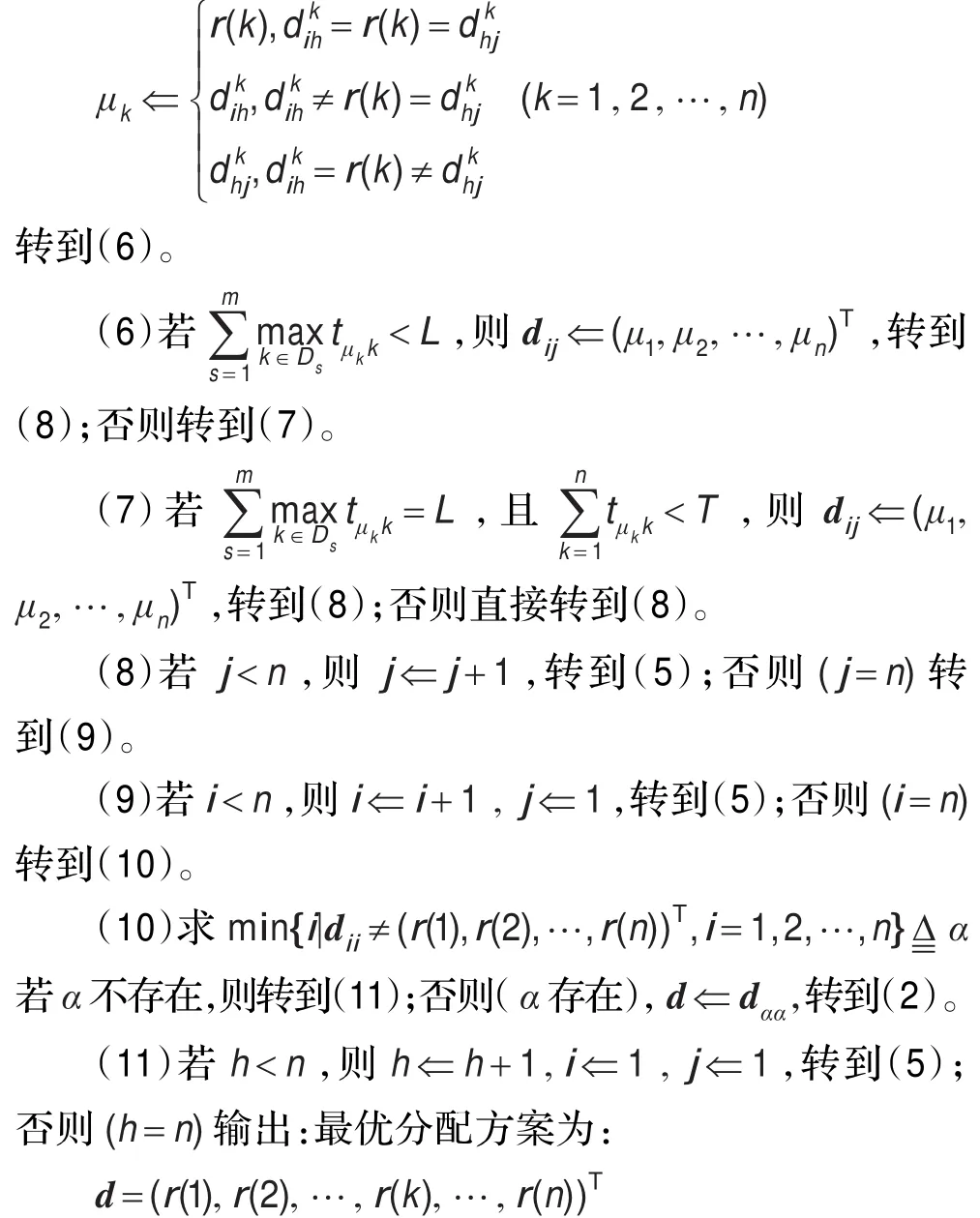
此时,最短工期为L;该最短工期下的最少总用时为T。
由上述算法步骤看出,步骤(1)给出初始可行分配方案的时间复杂度为O(n3),存储输入数据的空间复杂度为O(n2);步骤(3)构造当前可行分配方案下的立方检测矩阵的时间复杂度为O(n3),空间复杂度为O(n3);步骤(4)至步骤(11)按照Floyd算法的迭代次序进行迭代,理论上最坏情况下,迭代一次(即由一种可行分配方案变换到另一种工期更短或者工期不变但总用时更少的可行分配方案)的时间复杂度为O(n4),且最多迭代n!次。所以,本文给出的算法是一个时间复杂度为O(n!·n4)、空间复杂度为O(n3)的指数算法。
3.2 算法依据
定理设d是(P)的可行分配方案,(dij)n×n是对应的立方检测矩阵,则d为(P)的最优分配方案的充要条件是,对(dij)n×n按照算法步骤(4)至步骤(11)实施迭代运算,迭代过程中必有dii≡d(i=1,2,…,n)。
证明必要性(反证法)假设存在dii≠d,则由立方检测矩阵的定义和算法的迭代过程知,dii的初值为d,且随着迭代,dij对应的工期单调递减或者工期保持不变,但总用时单调递减。当i≠j时,dij不是可行分配方案,而i=j时,dij表示由第i项工作经过一个循环调整再重新回到第i项工作的分配方案,故dii(i=1,2,…,n)总是可行分配方案,而且dii对应的工期小于d对应的工期,或者dii对应的工期等于d的工期,但是dii对应的总用时小于d的总用时,这与d为最优分配方案矛盾。
充分性:由算法的迭代过程知,算法的迭代具有遍历性,并且随着迭代,dii对应的工期单调递减或者工期保持不变,但总用时单调递减。若dii≡d(i=1,2,…,n),则说明d对应的工期和总用时已经达到最优了,即d为最优分配方案。
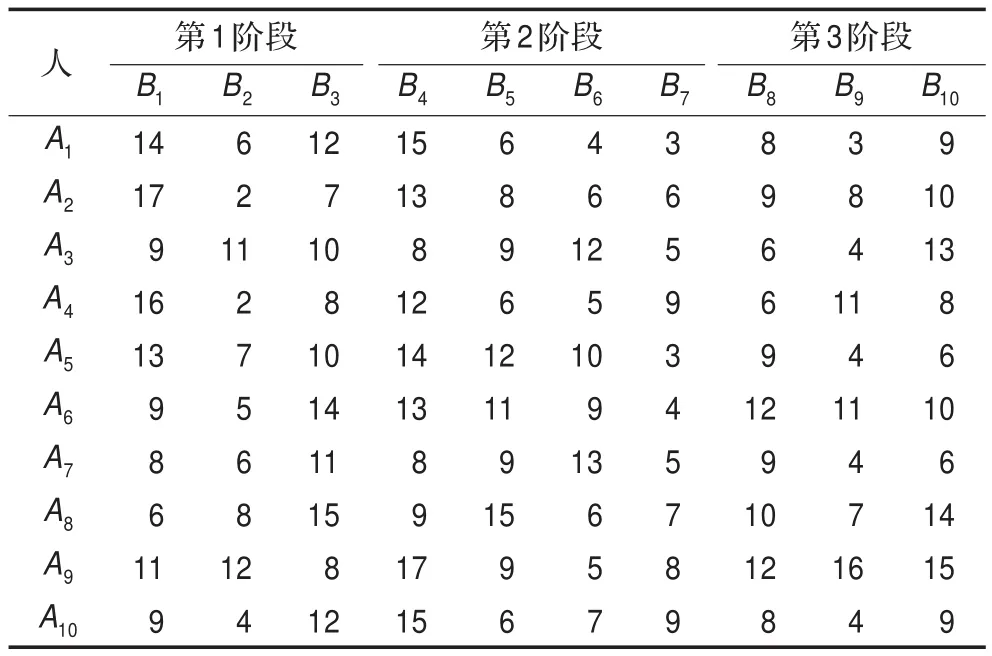
表1 第i人承担第j项工作的用时
4 算例演示
为了更加直观地显示和了解本文所给的算法,下面用一个例子来演示这种算法的运算过程和特点。
已知,n=10,m=3,a1=3,a2=4,a3=3,D1= {1,2,3},D2={4,5,6,7},D3={8,9,10},第i人承担第j项工作的用时矩阵(tij)10×10如表1所示,求工期最短的前提下使得总用时最少的最优分配方案。
解:由算法步骤(1)给出初始可行分配方案:d= (8,2,9,7,10,4,1,6,3,5)T,表示第8个人承担第1项工作,第2个人承担第2项工作,…,第5个人承担第10项工作。按照算法步骤(2)算出此时的工期为28,总用时为60。
按照算法步骤(3)写出该可行分配方案下的立方检测矩阵;接着按算法步骤(4)~(11)进行第1次迭代运算,迭代到i=8,j=8,h=1时,出现d88≠d,d88=(6,2,9,7,10,4,1,8,3,5)T,则d88不但是可行分配方案(表示第6个人承担第1项工作,第2个人承担第2项工作,…,第5个人承担第10项工作),而且d88对应的工期比d对应的工期更短。因此d⇐d88。转到步骤(2)知,d88对应的工期为27。
重复上述操作,至第9次(远远小于10!次)迭代时,知dii=d(i=1,2,…,10),即当前的可行分配方案d=(8,4,2,7,10,9,6,3,1,5)T是最优分配方案,表示第8个人承担第1项工作,第4个人承担第2项工作,…,第5个人承担第10项工作。此时最短工期为21,该最短工期下的最少总用时为53。具体的迭代过程和结果见表2。
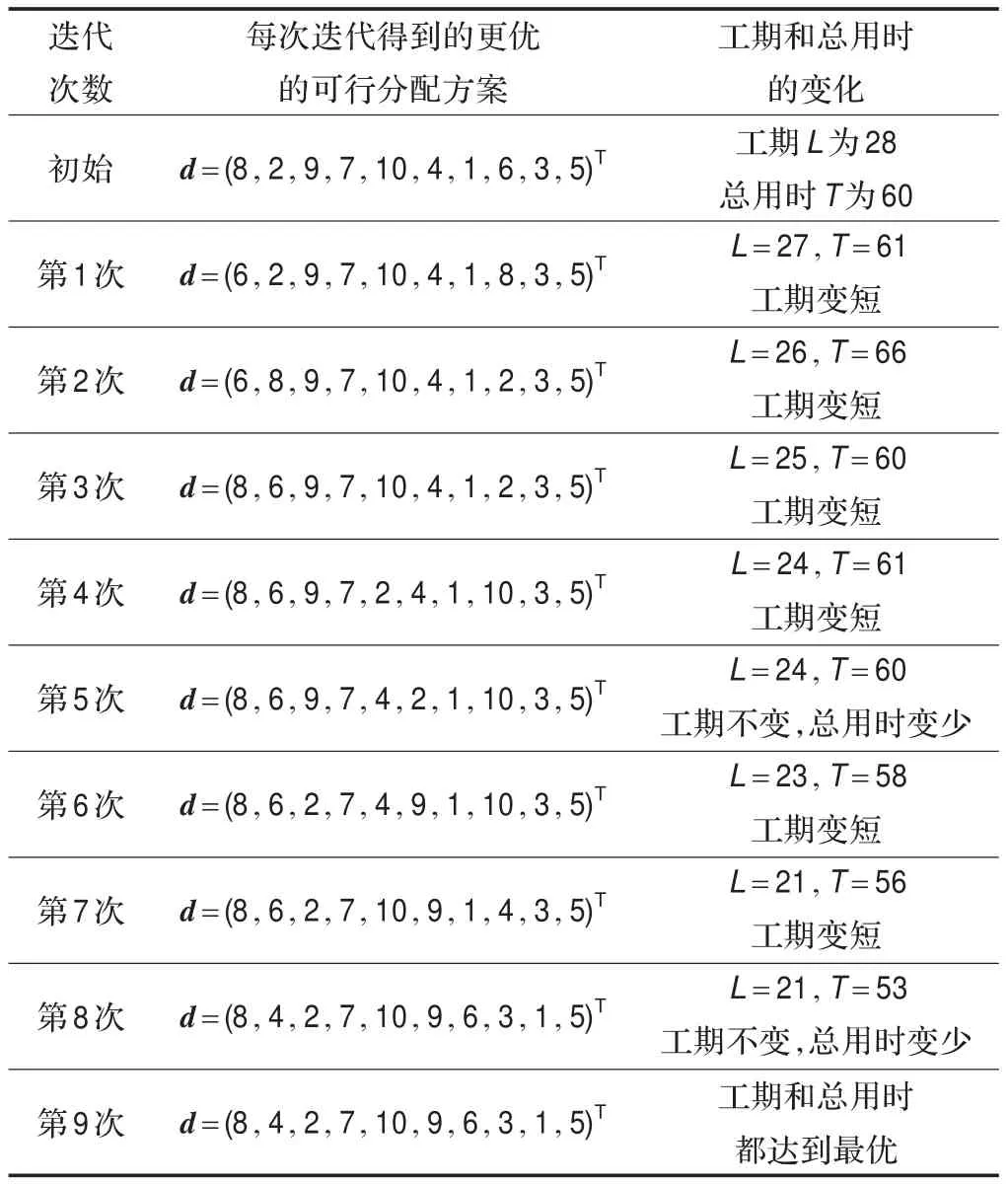
表2 迭代过程
5 结论
本文给出的多阶段双层目标分配问题属于NP完全问题,不存在多项式算法。本文给出的算法属于指数算法,但是其具备的单调迭代运算的特点,使其依然具有很好的运算效率,尤其是在问题的规模不是特别大的情况下。正如,求解线性规划(属于NP完全问题)的单纯形法,虽然属于指数算法,但其单调迭代运算的特征,使得至今没有任何一种求解线性规划的算法能够取代它。因此,本文针对多阶段双层目标分配问题给出的算法有很好的使用价值。另外,本文涉及的是一对一的多阶段双层目标分配问题,在此基础上,还可以进一步讨论一对多确定型的多阶段双层目标分配问题以及一对多非确定型的多阶段双层目标分配问题,这些分配问题同样有着广泛的应用背景。
[1]Pentico D W.Assignment problems:a golden anniversary survey[J].European Journal of Operational Research,2007,176(2):774-793.
[2]Kuhn H W.The Hungarian method for the assignment problem[J].Naval Research Logistics Quarterly,2005,52(1):7-21.
[3]郭强.分配问题的一种新的迭代算法[J].系统工程与电子技术,2004,26(12):1915-1916.
[4]郭强,陈新庄.平衡和不平衡运输问题与分配问题的通用迭代算法[J].运筹与管理,2007,16(6):57-62.
[5]李岩,郭强.非确定型指派问题的求解算法[J].计算机工程与应用,2009,45(15):61-63.
[6]Gross O.The bottleneck assignment problem[M].Santa Monica:The Rand Corporation,1959:16-20.
[7]Mazzola J B,Neebe A W.An algorithm for the bottleneck generalized assignment problem[J].Computer&Operations Research,1993,20(4):355-362.
[8]Aora S,Puri M C.A variant of time minimizing assignment problem[J].European Journal of Operational Research,1998,110(2):314-325.
[9]郭强.基于相关任务分配的网络计划的算法[J].计算机学报,2008,31(7):1138-1145.
[10]汪鸣鑫,周绍梅.基于暂态混沌神经网在非平衡B指派问题的应用[J].计算机工程,2006,32(23):205-207.
[11]Kyparisis G J,Koulamas C.Open shop scheduling with makespan and total completion time criteria[J].Computers&Operations Research,2000,27(1):15-27.
[12]Punnen A P,Aneja Y P.Categorized assignment scheduling:a tabu search approach[J].The Journal of the Operational Research Society,1993,44(7):673-679.
[13]Seshan C R.Some generalisations of time minimizing assignment problem[J].Journal of Operational Research Society,1981,32(6):489-494.
[14]Sonia,Puri M C.Two-stage time minimizing assignment problem[J].Omega,2008,36(5):730-740.
[15]Aggarwal V,Tikekar V G,Hsu L F.Bottleneck assignment problems under categorization[J].Computers&Operations Research,1986,13(1):11-26.
[16]钱颂迪.运筹学[M].北京:清华大学出版社,2005:80-82.
MA Qinqin,GUO Qiang,FU Xiaowei
College of Science,Northwestern Polytechnical University,Xi’an 710129,China
All jobs must be grouped into some stages and carried out successively,but jobs at the same stage can be commenced simultaneously.In this case,this paper researches how to allocate all jobs to the existing persons so as to minimize the completion time subject to the minimum makespan.A monotone decreasing iterative algorithm,which can obtain the precise optimal solution and has good computational efficiency,is proposed by introducing cubic detection matrix.
assignment problem;bi-objective;cubic detection matrix;iterative algorithm;precise optimal solution
A
TP301
10.3778/j.issn.1002-8331.1212-0219
MA Qinqin,GUO Qiang,FU Xiaowei.Precise algorithm of bi-objective assignment problem based on multi-stage. Computer Engineering and Applications,2014,50(21):44-47.
马芹芹(1986—),女,硕士研究生,研究领域为最优化理论与算法;郭强(1961—),男,副教授,研究领域为最优化理论与算法,运筹学与网络规划;付晓薇(1986—),女,硕士研究生,研究领域为最优化理论与算法。E-mail:18792710927@163.com
2012-12-18
2013-02-20
1002-8331(2014)21-0044-04
CNKI出版日期:2013-03-26,http://www.cnki.net/kcms/detail/11.2127.TP.20130326.1040.006.html

