60Co γ射线铅的吸收系数测量实验的数据拟合

张国强，边 纪，方 恺，张志华，杜 艾，赫 丽

(同济大学 物理科学与工程学院，上海 200092)

1 引 言

γ射线吸收系数的测定实验包括利用NaI(Tl)闪烁晶体探测器测定137Cs的能量为0.661MeV的γ射线以及60Co的能量为1.17 MeV和1.33 MeV的γ射线吸收系数[1-3]. 其中，NaI(Tl)闪烁晶体探测器得到的137Cs能谱中只有1个全能峰，数据处理时扣除能谱图的本底后，利用相应公式通过最小二乘法进行数据拟合就可以获得吸收系数.60Co γ射线包含能量为1.17 MeV 和1.33 MeV射线，相应地在NaI(Tl)闪烁晶体探测器得到的60Co能谱中就有2个全能峰. 教材中介绍了2种数据处理的方法：第一种方法是分别测量法：分别取1.17 MeV 和1.33 MeV射线的全能峰进行计算，获得2种射线各自的吸收系数. 这种方法中，由于2种射线的能量相差不大，全能峰的谱线相互重叠，NaI(Tl)闪烁探测器对γ射线很灵敏，造成本底计数比较高，无法准确地扣除本底，难以准确获得2个全能峰各自的吸收系数. 第2种方法是整体测量法：将2个全能峰作为整体来处理，测量能量为1.25 MeV的综合峰. 这种方法虽然解决了由于全能峰能谱相互交叠的问题，但无法单独确定2种能量峰的吸收系数.

基于以上2种方法，找到了一种新的数据处理方式，既可以分别测定60Co 1.17 MeV和1.33 MeV的γ射线吸收系数，同时又可以成功避免由于全能峰交叠带来的本底扣除的问题. 在新的方法中，首先测定60Co γ射线中2种不同能量射线的强度比；然后测定整体射线吸收系数与铅片的厚度之间的关系；再通过数据拟合，就可以求得2种射线各自的吸收系数. 利用这种新的方法测得的吸收系数，其相对误差小于原有的实验方法获得的结果.

近代物理实验是为高年级物理专业本科生开设的，培养学生的理论联系实际能力，综合实验能力和创新精神的课程，其教学方法与教学内容不断发展与丰富[4-5]. 本项工作是由本科生在完成讲义中的实验内容后，通过进一步分析思考而提出的，并将作为今后实验教学的拓展内容.

2 实验原理

2.1 NaI(Tl)闪烁晶体探测器工作原理

NaI(Tl)闪烁晶体探测器由闪烁体、光电倍增管和相应的电子仪器3部分组成[3]. 探测器的前端是NaI闪烁晶体，当射线进入闪烁体时产生次级电子，使闪烁体分子电离和激发，退激发时产生大量光子. 当闪烁光子入射到光电倍增管阴极上，由于光电效应就会产生光电子. 光电子受极间电场加速和聚焦，在各级打拿极上发生倍增，最后被阳极收集后产生电流脉冲.

2.2 γ射线的物质吸收系数

γ跃迁可定义为核由高激发态到较低的激发态，而原子序数和质量数均保持不变的退激发过程. γ射线与物质的相互作用在单次事件中便能导致完全的吸收或散射. 本实验研究的对象为窄束γ射线，不考虑散射成分，并可认为窄束γ射线穿透物质时能量不变，而强度逐渐减弱.

γ射线的强度随厚度的衰减服从指数规律[6]，即：

I=I0e-ux=I0e-uR/ρ,

(1)

式中，I0和I分别为穿过物质前后γ射线的强度，x是物质厚度，u是该物质线性吸收系数. 为了消除密度影响，引入质量厚度R=ρx来表示吸收体厚度，其中ρ为物质的密度. 由于在相同实验条件下，某一时刻计数率N总与该时刻的γ射线强度I成正比，则

N=N0e-uR/ρ,

(2)

则吸收系数u为

(3)

这种求吸收系数的方法可应用于计算具有单一能量的γ射线(如137Cs放射源发出的γ射线)的吸收系数.

60Co放射源发出的γ射线包含能量为1.17 MeV的射线1和能量为1.33 MeV的射线2，利用(2)式可得：

N0e-ux=N0αe-u1x+N0(1-α)e-u2x,

(4)

其中，u1和u2分别为该材料对单能射线1、射线2的吸收系数,α与1-α分别为射线1、射线2的初始射线强度与总强度之比. 由(4)式得：

(5)

其中

(6)

可以通过测定初始时2种射线强度确定α.

这时的吸收系数u与物质厚度x有关. 测定了u和x之间的关系后，就可以利用数值拟合的方法，确定2种射线各自的吸收系数u1和u2.

3 实验内容和数据处理

3.1 实验内容

实验装置和器材包括：a.γ放射源60Co≈1.5 μC；b.200 μm Al窗NaI(Tl)闪烁探头；c.Pb吸收片若干. 实验调节和测量步骤包括：1)调整实验装置，使放射源、准直孔、闪烁探测器的中心位于一条直线上；2)在闪烁探测器和放射源之间加上0,1,2…片已知质量厚度的吸收片，进行定时测量，并保存实验谱图；3)计算所要研究的光电峰净面积Ai，Ai对应公式中的Ii和Ni，其值为总面积Ag和本底Ab的差值；4)分别用数据拟合法和原来的分别测量法计算两种射线的吸收系数，与2种射线的标准吸收系数进行比较.

3.2 数据处理方法

数据处理的关键是双峰净面积的确定. 如图1所示[3]，分别测量法测量60Co的双能射线吸收系数时，A1和A2分别为全能峰1和峰2的净面积，Aa和Ab为相应的本底. 数据拟合法确定的测量60Co的双能射线吸收系数时，总的净面积为全能峰1和峰2的净面积之和，总的本底为全能峰1和峰2的本底之和.

图1 Co源双峰本底示意图

4 实验结果与讨论

4.1 1.17 MeV射线强度与总射线强度比值

在放射源和NaI(Tl)单晶γ闪烁晶体探测器之间不放置铅板时，测得60Co能量为1.17 MeV和1.33 MeV的2种γ射线的综合峰的净面积N0=5 330，其中能量为1.17 MeV的γ射线的全能峰的净面积N10=2 658，则1.17 MeV射线强度与总射线强度比值α为

(7)

实际上，60Co经过1次β衰变成为处在2.5 MeV激发态的60Ni,60Ni的激发态的寿命极短，它放出能量分别为1.17 MeV和1.33 MeV的2种γ射线而跃迁到基态[7].

4.2 数据拟合法确定γ射线单能射线吸收系数

实验数据如表1所示，利用式(5)，通过Mathematica计算软件的FindFit函数做数值拟合，得出1.17 MeV射线的吸收系数u1和1.33 MeV射线的吸收系数u2：

u1=0.736 cm-1,u2=0.675 cm-1.

通过数据拟合的结果可知，铅元素对1.17 MeV射线的吸收系数大于1.33 MeV射线的吸收系数.

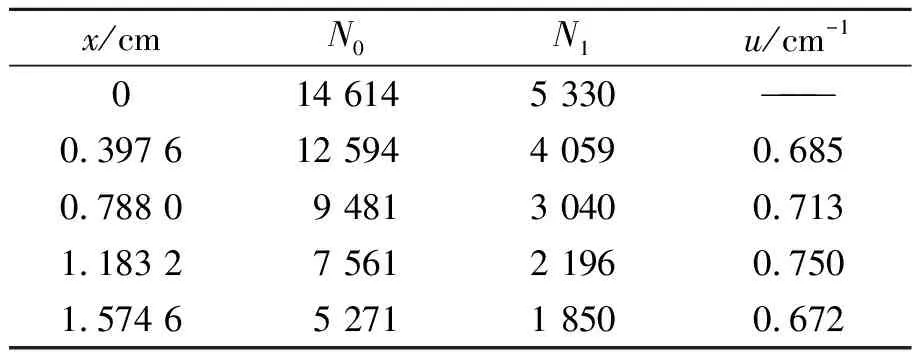
表1 确定总吸收系数u与铅块厚度x之间关系

4.3 用分别测量法确定γ射线单能吸收系数

利用式(1)，通过最小二乘法拟合数据并作图2. 由图2可知，随着铅块厚度的增加，2种能量射线的强度都在变弱. 从图2中可以得到能量为1.17 MeV和1.33 MeV射线的吸收系数u1′和u2′分别为0.837 cm-1和0.539 cm-1.

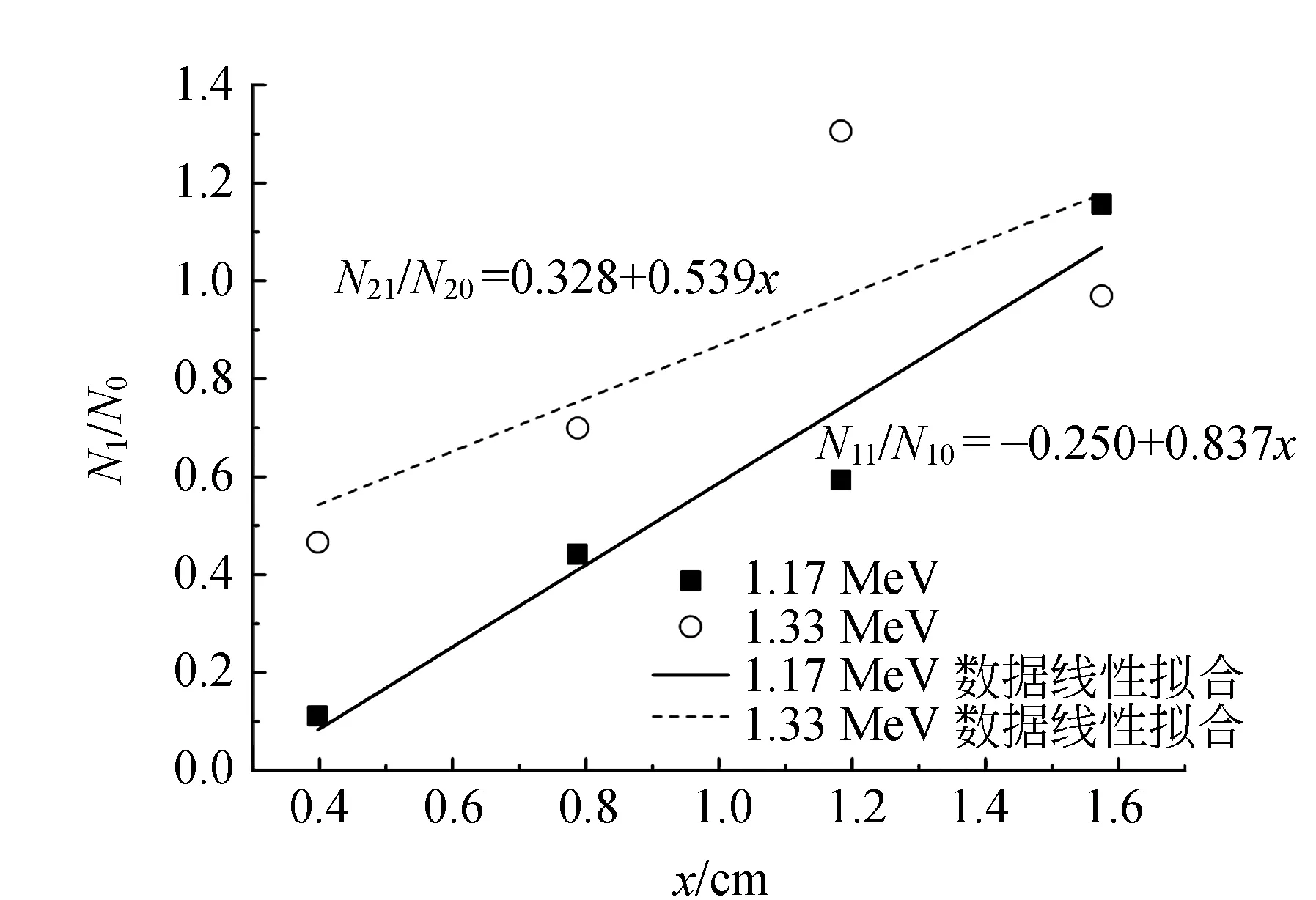
图2 铅片厚度x与N/N0关系

4.4 比较2种方法测量结果

由参考文献[8]中提供的γ射线的能量E(MeV)和吸收系数u(cm-1),分别是(0.5,1.640),(1.0,0.776),(1.5，0.581)和(2.0,0.518)[6]. 利用Mathematica软件FinfFit函数进行拟合，可得能量E和吸收系数u的关系为

u(E)=537.879e-0.306(E+3.994)2+0.553 .

(8)

由式(8)作图，可得图3中的u1曲线，并分别用u2和u3标注出拟合法和分别测量法得到的γ射线的吸收系数. 根据此式即可计算出1.17 MeV和1.33 MeVγ射线吸收系数分别为0.707 cm-1和0.642 cm-1，以此作为吸收系数u的标准值.

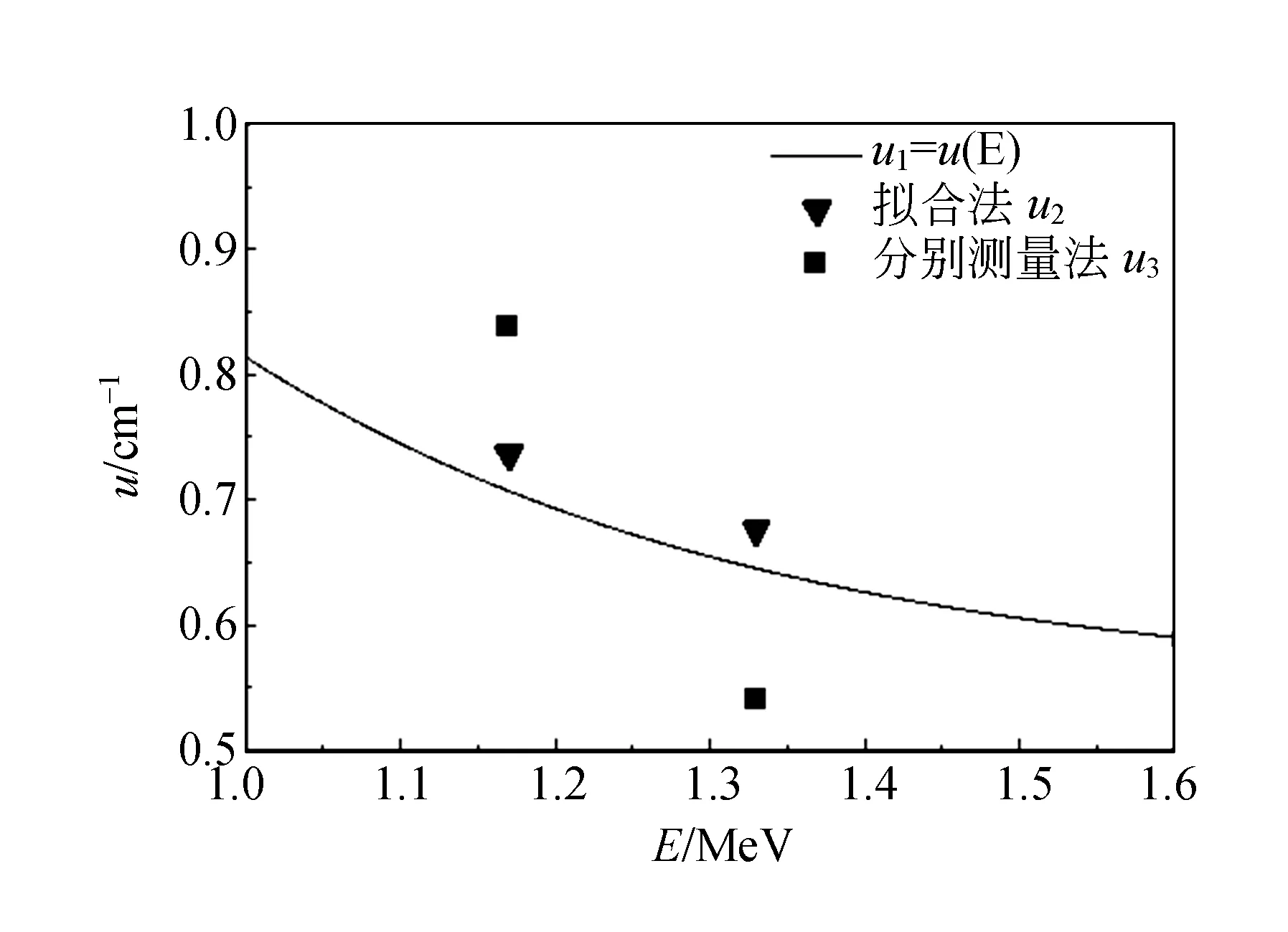
图3 γ射线吸收系数与能量的关系

将用拟合法、分别测量法获得的结果与标准值相比较[6]，由表2可知，数据拟合法得出的结果误差较小，与分别测量相比有显著的优点.

表2 比较两种方法测量u1和u2的误差

5 结 论

本文提出了计算γ射线物质吸收系数的新方法. 通过用2种方法分别测量铅对1.17 MeV和1.33 MeV两种60Co γ射线的吸收系数并与标准值进行对比发现，数值拟合法测得u1和u2值相对误差远小于分别测量所得的值. 由此可以看出，对于测量含多种能量谱线的γ射线中各个能量射线的吸收系数来说，数值拟合法是一种全新的方式.

参考文献：

[1] 谢筱翊，陈玲燕. 相对论效应实验中的数据处理[J]. 物理实验,1990，10(2)：51-54.

[2] 陈玲燕，顾牡，秦树基,等. 相对论效应实验谱仪的系列教学实验[J]. 物理实验,2000，20(3)：3-5.

[3] 同济大学物理实验中心. 近代物理实验讲义[Z]. 2013:78-98.

[4] 任红，谢莉莎，刘彩霞，等. 近代物理实验教学与考试效果分析评价体系研究[J]. 物理实验，2013，33(7)：14-19.

[5] 顾恩遥，白翠琴，吕景林. 冉绍尔-汤森效应实验仪自动化改进[J]. 物理实验，2013，33(11)：11-15.

[6] 黄新民，解挺. 材料分析测试方法[M]. 北京：国防工业出版社，2008.

[7] 杨福家. 原子物理学[M]. 北京：高等教育出版社，2008：356.

[8] 刘克桓. 物理教师手册[M]. 北京：人民教育出版社，1998:980-981.