准稳态问题的热流密度分析

罗 宏

(苏州科技学院 数理学院，江苏 苏州 215009)

1 引 言

热传导的准稳态过程广泛存在于自然界. 在耗能领域，准稳态模型被用在热传导的建模研究中，达到提高热效率，充分利用能源的目的[1-2]，或减小热能损失，节约能源的目的[3-4]. 由于效率和精度上的优点，在材料的物性测量中准稳态亦有较多的应用[5-8]. 关于温度场分析，也可以应用准稳态的模型[9-10]. 准稳态问题常用的理论分析方法是解含有特定边界条件和初始条件的热传导微分方程

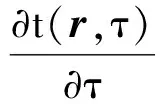
(1)

需用到偏微分方程、傅里叶分析等数学工具，过程较复杂[11]. 文献[12]分析了第二类边界条件下的无限大平行平板中的准稳态热传导过程. 本文则讨论了由对称性可知物体热流密度线分布的情况下，如何求出热流密度沿热流密度线变化的函数，再由热流密度函数得到物体内的温度场函数及导热系数公式. 这种方法简单、直观、效率较高、物理概念清晰. 以下假设在各向同性的均匀介质中，导热系数λ、比热容c和材料密度ρ不随温度变化.

2 方法介绍

一受热物体，如果表面各处热流密度恒定，物体内热源的发热效率恒定，则此物体存在准稳态热传导过程[13]. 准稳态下，由于物体中各处温升速度相同[5,13]，则温度梯度不随时间变化，由傅里叶定律

q=-λt(r,τ)

(2)

可知，物体各点的热流密度不随时间变化. 沿着热流密度的方向前进，会在物体内得到一条曲线，本文称之为热流密度线. 由以上分析，准稳态物体中的热流密度线是固定不动的. 只要知道了物体中热流密度线的分布，则可以推出热流密度沿热流密度线的变化. 现假设已经知道了热流密度沿热流密度线的变化，则可由(2)式的变形式

(3)

沿热流密度线上起点c到任一点x积分，就可得到x点的温度

(4)

由此得到沿热流密度线的温度场分布. 式中s为沿热流密度线的自然坐标. 同时，如果测得热流密度线首尾两端的温度差,沿整条热流密度线积分，就可以得到导热系数的表达式为

(5)

式中c点、e点分别代表热流密度线的首尾两端，分母中的温度差在准稳态下为常量. 由此推得温度场函数和导热系数的表达式. 以下说明已知热流密度线的空间分布，计算热流密度q(x)的方法.

假设热流密度线的路径为已知. 则如图1所示，取体系中任意一条热流密度线cxe,首尾两端c点和e点的热流密度已知(通常此二点位于物体表面).c点热流密度为qc，e点热流密度为qe. 以cxe为边，在其附近取一微小柱体，使热流密度线不穿过柱体表面，柱体表面都由热流密度线构成，则此微小柱体就像一个管道，热量在其中流动，管道内外没有热量交换，本文中称这样的柱体为热流管道.c点处，垂直于cxe的截面(即等温面)，面积为A1；x点处的等温截面面积为A2，热流密度设为q(x)；e点处等温截面面积为A3. 由于此管道极细，则各截面上的热流密度即为cxe线上对应点的热流密度.A1与A2之间的体积为V1，其内部热源发热效率为Q1.A2与A3之间的体积为V2，其内部热源发热效率为Q2. 发热效率以流入物体为正，热流密度按图示方向为正. 以下求q(x).

图1 热流管道微元

由比热容的定义

ΔQ=cmΔt,

(6)

及能量守恒定律，在V1内，流入的净热量决定升高的温度

qcA1+Q1-q(x)A2=cρV1Δt,

(7)

式中ρ为材料的密度，Δt为单位时间内V1升高的温度. 同理在整个柱体内有

qcA1+Q1+Q2-qeA3=cρ(V1+V2)Δt,

(8)

由于准稳态下物体内部各处温升速度相同，所以上两式中Δt相同. 从两式中消去Δt可得到q(x)

(9)

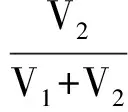
3 示例：长的空心圆柱体

以满足第二类边界条件、准稳态下的长空心圆柱体为例，来说明如何运用以上方法求温度分布及导热系数. 文献[6]中正是使用这样的测量系统.

图2 无限长圆柱体截面图

(10)

此为空心圆柱体内半径为x的圆面上的热流密度. 将(10)式代入(4)式，沿径向积分就得到柱体内的温度分布

(11)

此柱体达到准稳态后，相同半径x的圆面上，温度都相同. 将x=R代入(11)式或将(10)式代入(5)式可得

(12)

为长空心圆柱体内的导热系数表达式，式中Δt=t(R)-t(r)为内外表面的温度差，在准稳态下为常量.

4 结束语

热流密度和温度场之间的关系由(2)式的傅里叶定律提出. 由此，可以由温度场出发，进而分析热流密度等其他物理量或物理效应. 也可以由热流密度出发来分析. 本文选择后一种方法. 在准稳态下，物体内温升速度不随时间变化，即热流密度不随时间变化，由时间不变量出发分析问题有其便捷性. 另外，由热流密度可以直接和能量守恒定律相联系，为分析解决问题带了了便利. 本文分析准稳态的方法简单直观、效率高. 其缺点是，需首先由对称性或其他方法得到物体内热流密度曲线的路径. 对于由对称性分析可以知道物体中热流密度线路径的问题，可以快速得到其热流密度函数、温度场分布和导热系数的表达式. 对于可以估计热流密度线路径的问题，则可以对物体内的温度分布、热流密度做初步的评价. 另外，从这一方法出发，可以定性地分析准稳态下体系热流以及温度场的一些性质. 对于热物性测量仪器的设计及工程问题中的热流和温度场分析都有帮助.

参考文献：

[1] Fardoun F, Ibrahim O, Zoughaib A. Quasi-steady state modeling of an air source heat pump water heater[J]. Energy Procedia, 2011(6):325-330.

[2] Khandekar S, Gautam A P, Sharma P K. Multiple quasi-steady states in a closed loop pulsating heat pipe [J]. International Journal of Thermal Science, 2009,48(3):535-546.

[3] Wauman B, Breesch H, Saelens D. Evaluation of the accuracy of the implementation of dynamic effects in the quasi steady-state calculation method for school buildings[J]. Energy and Buildings, 2013,65(8):173-184.

[4] Medina M A. A quasi-steady-state heat balance model of residential walls[J]. Mathematical and Computer Modelling, 1999(30):103-112.

[5] 郭重雄，余其铮，薛洪福. 导热系数和比热准 稳态测量方法的分析[J]. 哈尔滨工业大学学报，1984(2):62-72.

[6] 赵小明，陆世豪，顾兆林,等. 准稳态理论测量溶解热及比热容的实验研究[J]. 西安交通大学学报，2005,39(9):958-961.

[7] 周乐平，王补宣. 准稳态法测量纳米颗粒悬浮液的热物性[J]. 工程热物理学报，2003,24(6):1038-1039.

[8] 张红佳，郭永利，李正,等. 真空热流法测定不良导体的导热系数[J]. 物理实验，2012,32(9):5-7.

[9] 殷鹏飞，张蓉，熊江涛,等. 搅拌摩擦焊准稳态热力耦合过程数值模拟研究[J]. 物理学报，2013,62(1)：1-8.

[10] 赵福海，华学明，叶欣,等. 热丝TIG焊热丝准稳态温度场的解析模型[J]. 上海交通大学学报，2012,46(7):1063-1068.

[11] 雷柯夫 A B. 热传导理论[M]. 裘烈钧，丁履得译. 北京：高等教育出版社，1955:55-71，151-176.

[12] 罗宏. 用傅里叶定律分析无限大平行平板中的准稳态[J]. 物理实验，2014,34(8)：31-33.

[13] 胡汉平. 准稳态温度场存在的充要条件[J]. 应用科学学报，2004,22(1):91-93.