3排管冻结梯形-抛物弓叠合等效温度场模型和平均温度
胡向东,任 辉
(1.同济大学 地下建筑与工程系,上海 200092;2.同济大学 岩土及地下工程教育部重点实验室,上海 200092)
3排管冻结梯形-抛物弓叠合等效温度场模型和平均温度
胡向东1,2,任 辉1,2
(1.同济大学 地下建筑与工程系,上海 200092;2.同济大学 岩土及地下工程教育部重点实验室,上海 200092)
由于3排管冻结温度场的复杂性,不便于对冻土帷幕温度场进行简便描述。故以现有的3排管冻结温度场的势函数叠加法解析解为理论基础,根据温度场的周期性,选择主面与界面之间的合适位置作为等效截面,以等效截面的温度场等效整体温度场。以平均温度为检验标准,简化等效截面的温度场曲线,得出方便应用的梯形抛物弓叠合等效温度场模型。基于等效温度场模型确定平均温度计算方法,得出免于积分运算的平均温度简便计算公式。该公式计算精度满足工程要求,表明等效温度场及其平均温度计算方法具有良好的实用性。
3排管冻结;等效温度场;平均温度;冻土帷幕;人工地层冻结法
冻结温度场的研究是人工地层冻结法理论研究的基础,也是冻结设计施工的理论依据。随着人工地层冻结法在矿山建设、城市地下工程和河底隧道工程中的广泛应用,单排冻结管温度场以及双排冻结管温度场的研究取得了一系列成果[1-3],笔者也进行了单、双排管冻结温度场及其平均温度的完善和应用性研究[4-10]。
由于工程实践的需要,为了实现厚度较大和平均温度较低的冻土帷幕,多排(3排及3排以上)管冻结方案被广泛地应用于大水流地层矿山井筒和深井冻结、盾构进出洞地基加固等工程中。但是对多排管冻土帷幕温度场及其平均温度计算方法的研究极少,有学者通过数值模拟获得了经验公式[11],笔者基于巴霍尔金解析解的双排管冻结温度场公式通过作图的方法应用于描述多排管冻土帷幕温度场,并得到多排管冻土帷幕厚度及平均温度的计算公式[12]。也有学者在上海地铁某一区间隧道修复采用四排局部垂直冻结时,对冻结壁温度场发展进行实时监测,分析多排管局部冻结冻土壁温度场特性[13],但没有对多排管冻土壁进行深入的理论研究。工程界也有采用计算单排管冻土帷幕平均温度的“成冰”公式[14]近似计算多排管冻土帷幕平均温度的情况。故笔者针对3排管冻结温度场进行研究,得出3排管冻结温度场的势函数叠加法解析解,并验证了其解析解结果的可靠性[15]。考虑3排管冻结温度场的复杂性,为方便研究冻土帷幕力学性能和指导冻结设计施工,笔者将以3排管冻结温度场解析解为理论基础,探求3排管冻土帷幕的在二维平面的等效温度场模型。
1 3排管冻结温度场
3排管冻土帷幕冻结管布置方式一般可分为两大类:一为3排冻结管直线型对齐排布,二为相邻两排冻结管管间距错开l/2排列,成为3排冻结管直线型交错排布,如图1所示。
根据3排管冻结温度场的势函数叠加法解析解理论[15],以图1所示坐标系(xoy)为准,3排管冻土帷幕稳态温度场分布的解析解表达式为

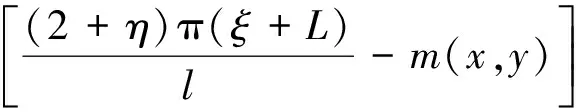
(1)
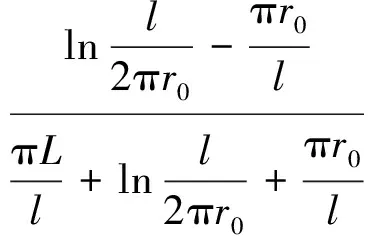
式中,t(x,y)为任意点(x,y)的温度,℃;tct为冻结管表面的温度,℃;l为每排两根冻结管的间距,m;L为3排冻结管的排距,m;ξ为每排冻结管至冻土墙边缘的冻土厚度,m;r0为冻结管外半径,m;ω为区别3排管两种排列方式的符号:对于3排冻结管对齐排列,ω=1;对于3排冻结管交错排列,ω=-1。
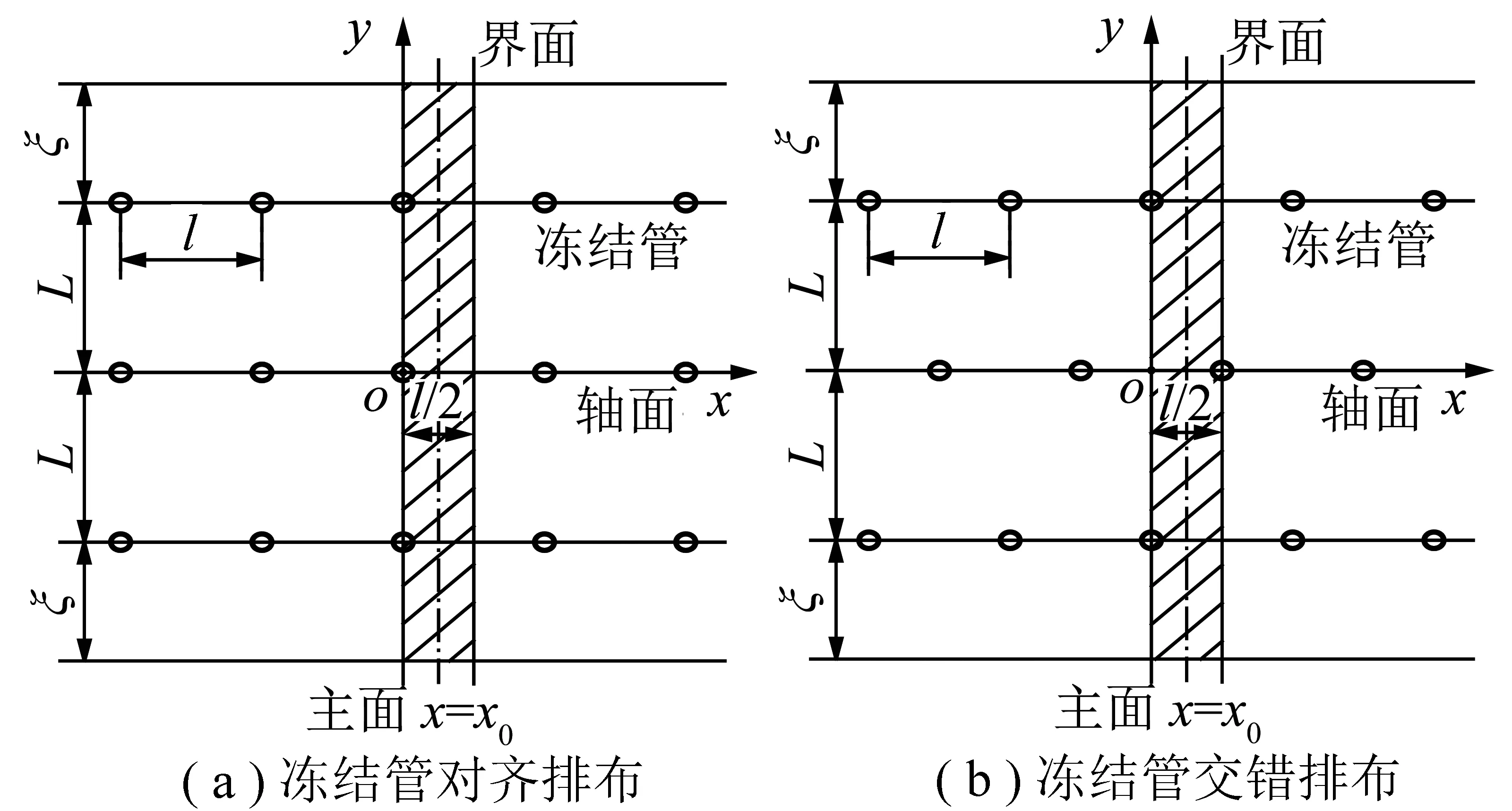
图1 3排管冻土帷幕冻结管布置方式Fig.1 Arrangement of three-row-pipe freezing
2 3排管等效温度场
2.1 等效温度场的确定
不论从式(1)还是图2都可以直观地看出3排管冻土帷幕的温度场的复杂,不利于理论研究和工程应用,为此我们希望找出一个等效截面x=xe,并以此截面上的温度t(xe,y)来替代真实温度场。

图2 3排管冻土帷幕温度场示意Fig.2 Temperature field distribution of three-row-pipe freezing
考虑冻结管布置的对称性,及温度场在x轴上的周期性,整个冻土帷幕只需要研究其中0≤x 分析式(1)可知,当冻结管外半径和冻结管分布形式确定时,整个冻土帷幕的温度场主要受冻结管间距l、冻结管排距L、冻结管至冻土墙边缘的冻土厚度ξ的影响,针对上述3个参数的不同取值,利用式(1)计算结果考察0≤x 选取x=0,l/6,l/4,l/3,l/2这5个特征截面,观察其冻土帷幕温度曲线t(x,y)的分布情况。根据冻结管两种不同排布方式,选择不同参数取值得到352组冻土帷幕的5个特征截面温度分布情况,参数具体取值详见表1。观察每组数据的温度曲线可知,在相同的冻结管排布方式下,曲线的形状都是类似的。故针对冻结管两类不同排布方式,选取1组参数(L=1.0m,l/L=1.0,ξ/L=0.5)为例进行具体说明,描述这5个特征截面的温度分布情况,如图3所示。 表1参数取值 参数取值L1 0,1 2,1 4,1 6ml/L0 7,0 8,0 9,1 0ξ/L0 5,0 6,0 7,0 8,0 9,1 0,1 1,1 2,1 3,1 4,1 5 图3 特征截面冻土帷幕温度场Fig.3 Temperature field distribution of the characteristic cross-sections 根据图3显示可知,3排管在主面(x=0)与界面(x=l/2)之间不同截面的温度场主要是在冻结管位置温度变化较大,尤其是3排管外面两排冻结管位置温度变化更明显,并且在主面(x=0)到截面(x=l/6)温度变化梯度最大,随后逐渐减小,这就表明在冻结管位置从主面(x=0)到界面(x=l/2)温度是迅速升高,使得截面温度曲线趋于一致。由此可知,仅主面附近小部分范围因靠近冻结管温度较低,使得此部分截面温度曲线在冻结管位置有较大变化,而其他大部分截面温度曲线型状基本类似。因此,考虑用其中某一特征截面的温度曲线来近似描述整个温度场的温度变化情况,此特征截面即为等效截面,笔者拟采用主面(x=0)与界面(x=l/2)之间的中间位置(xe=l/4)作为等效截面。 根据上述分析结果,xe=l/4特征截面作为等效截面来描述整个冻土帷幕温度场,但xe=l/4代入式(1)后所得温度场公式仍然很复杂,故对特征截面(xe=l/4)进行处理,观察xe=l/4的温度曲线,可将温度曲线简化为如图4所示的等效温度曲线(在参数相同的情况下,xe=l/4截面的对齐排布和交错排布温度曲线一致),曲线分上下两部分,上部分为抛物弓型状,下部分为等腰梯形型状,抛物弓顶点和梯形顶点位置温度取特征截面xe=l/4所对应的温度,分别为t(l/4,0)和t(l/4,L),此时等效温度曲线可表示为 (2) 其中: 式(2)即为等效温度场分布的表达式。 图4 等效温度场示意Fig.4 Temperature field distribution of the equivalent model 2.2 等效温度场的验证 等效温度场与真实温度场等效的标准有2条:① 在等效截面上等效温度场曲线与真实温度场曲线吻合;② 等效温度场的平均温度与真实温度场的平均温度相等。第①条标准由等效温度场曲线的定义(式(2))已经满足,由图4已可见。以下对第②条标准进行验证。 (1)以3排管冻结温度场的势函数叠加法解析解为理论基础,根据冻结管布置的对称性及温度场在x轴上的周期性,整个冻土帷幕的平均温度等于0≤x (3) (4) 图5 冻土帷幕平均温度计算结果比较Fig.5 Comparison of calculated average temperature 从图6可以看出,相对误差位于2.61%~4.95%,误差控制在5.0%以内,且随着l/L的增大,误差增大,随着ξ/L的增大,误差减小。 图6 等效温度场平均温度的误差Fig.6 Accuracy of average temperatures of the equivalent temperature field 3.1 平均温度计算公式 上一节采用平均温度这一指标来验证等效温度场的准确性,据此,可以导出冻土帷幕平均温度的近似简单求解方法,就是利用等效温度场来替代真实的温度场,联合式(2),(4)得 (5) 其中 3.2 平均温度计算公式的适用性 人工地层冻结过程是一个瞬态热传导过程,是个具有相变并且相变界面移动的问题。然而本文计算公式由于是基于3排管冻结稳态温度场解析解[15],其适用性值得注意。对于采用稳态温度场近似瞬态温度场的适用性问题,学术界和工程界普遍接受的观点是:由于人工地层冻结是个发展相对缓慢的过程,尤其是在冻结的后期,其温度场非常接近稳态导热温度场,在人工地层冻结法的温度场理论与工程中,对此状态可按稳态导热近似求解人工冻结温度场。世界上最流行和实用的人工冻结温度场解析解有前苏联[1]、美国[2]和日本[3]公式,他们均为稳态温度场公式。对此问题,笔者曾针对文献[1]的单排管和双排管冻结巴霍尔金公式的准确性进行了分析[9],结果表明,在冻结的中后期(ξ/l> 0.7),温度场任何一点的计算误差不超过1℃。作为本文基础的3排管冻结温度场公式[15]与巴霍尔金公式基本特征相同,因此可以推测,在冻结的中后期,本文计算公式具有足够的准确性。 (1)以3排管温度场解析解为基础,建立了等效温度场模型,即找到一个等效截面,以等效截面的温度场替代整体温度场。将此截面温度场分布图形简化为由上下两部分构成的图形,上部分为抛物弓,下部分为等腰梯形。 (2)利用平均温度验证等效温度场的准确性。等效温度场的平均温度和解析解温度场的平均温度两者的对比分析表明,等效温度场平均温度计算结果的相对误差不超过5.0%,精度满足工程要求,表明等效温度场具有良好的实用性。 (3)基于等效温度场,建立了3排管冻土帷幕平均温度计算公式。该公式为免于积分计算的简便公式,计算准确,且结果偏于安全。 [1] Bakholdin B V.Selection of optimized mode of ground freezing for construction purpose[M].Moscow.State Construction Press,1963. [2] Sanger F J.Ground freezing in construction[J].Journal of the Soil Mechanics and Foundations Division,1968,94(SM1):131-158. [3] 戸部暢,秋元攻.凍土内温度分布計算式と,その応用[J].冷凍,1979,54(622):3-11. Tobe N,Akimoto O.Temperature distribution formula in frozen soil and its application[J].Refrigeration,1979,54(622):3-11. [4] 胡向东,黄 峰,白 楠.考虑土层冻结温度时人工冻结温度场模型[J].中国矿业大学学报,2008,37(4):550-555. Hu Xiangdong,Huang Feng,Bai Nan.Models of artificial frozen temperature field considering soil freezing point[J].Journal of China University of Mining & Technology,2008,37(4):550-555. [5] 胡向东,白 楠,余 锋.单排管冻结温度场ТРУПАК和БАХОЛДИН公式的适用性[J].同济大学学报(自然科学版),2008,36(7):906-910. Hu Xiangdong,Bai Nan,Yu Feng.Analysis of Trupak and Bakholdinformulas for temperature field of single-row-pipe frozen soil wall[J].Journal of Tongji University(Natural Science),2008,36(7):906-910. [6] 胡向东.直线形单排管冻土帷幕平均温度计算方法[J].冰川冻土,2010,32(4):778-785. Hu Xiangdong.Average temperature calculation for the straight single-row-pipe frozen soil wall[J].Journal of Glaciology and Geocryology,2010,32(4):778-785. [7] 胡传鹏,胡向东,朱合华.单排管冻结巴霍尔金温度场控制参数敏感度分析[J].煤炭学报,2011,36(8):938-944. Hu Chuanpeng,Hu Xiangdong,Zhu Hehua.Sensitivity analysis of control parameters of Bakholdin solution in single-row-pipe freezing[J].Journal of China Coal Society,2011,36(8):938-944. [8] Hu Xiangdong.Average temperature model of double-row-pipe frozen soil wall by equivalent trapezoid method[A].API Conference Proceedings[C].2010,1233:1333-1338. [9] 胡向东,赵俊杰.人工冻结温度场巴霍尔金模型准确性研究[J].地下空间与工程学报,2010,6(1):96-101. Hu Xiangdong,Zhao Junjie.Research on precision of Bakholdin model for temperature field of artificial ground freezing[J].Chinese Journal of Underground Space and Engineering,2010,6(1):96-101. [10] 胡向东,赵 飞,佘思源,等.直线双排管冻结壁平均温度的等效抛物弓形模型[J].煤炭学报,2012,37(1):28-32. Hu Xiangdong,Zhao Fei,She Siyuan,et al.Equivalent parabolic arch method of average temperature calculation for straight double-row-pipe frozen soil wall[J].Journal of China Coal Society,2012,37(1):28-32. [11] 彭益成,胡向东.丁文其.多排管冻土帷幕平均温度特征与计算方法[J].低温建筑技术,2009,36(10):89-91. Peng Yicheng,Hu Xiangdong,Ding Wenqi.Characteritics and calculation method of average temperature for multi-row-pipe frozen soil wall[J].Low Temperature Architecture Technology,2009,36(10):89-91. [12] 胡向东,何挺秀.多排管直线冻土墙平均温度的等效梯形计算方法[J].煤炭学报,2009,34(11):1465-1469. Hu Xiangdong,He Tingxiu.Equivalent-trapezoid method of average temperature calculation for multi-row-pipe straight frozen soil wall[J].Journal of China Coal Society,2009,34(11):1465-1469. [13] 肖朝昀,胡向东,张庆贺.多排管局部冻结冻土壁温度场特征[J].岩石力学与工程学报,2007,26(S1):2694-2700. Xiao Zhaoyun,Hu Xiangdong,Zhang Qinghe.Characters of temperature field in frozen soil wall with multirow freeze-tubes and limited depth freezing[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(S1):2694-2700. [14] 陈文豹,汤志斌.潘集矿区冻结壁平均温度及冻结孔布置圈径的探讨[J].煤炭学报,1982(1):46-52. Chen Wenbao,Tang Zhibin.The average temperature in ice wall and the diameter of frozen circle in Panji coal field[J].Journal of China Coal Society,1982(1):46-52. [15] 胡向东,汪 洋.三排管冻结温度场的势函数叠加法解析解[J].岩石力学与工程学报,2012,31(5):1071-1080. Hu Xiangdong,Wang Yang.Analytical solution of three-row-piped frozen temperature field by means of superposition of potential[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(5):1071-1080. Atrapezoidal-parabolicarchsuperimposedequivalenttemperaturefieldmodelanditsaveragetemperatureformulafortriple-row-pipefreezing HU Xiang-dong1,2,REN Hui1,2 (1.DepartmentofGeotechnicalEngineering,TongjiUniversity,Shanghai200092,China.2.KeyLaboratoryofGeotechnicalandUndergroundEngineeringofMinistryofEducation,TongjiUniversity,Shanghai200092,China) The temperature field of triple-row-pipe freezing is difficult and inconvenient to be described simply due to its complexity.Based on the existing analytical solution of triple-row-pipe frozen temperature field,according to the periodicity of the temperature field,an appropriate position between the main section and the intersection was chosen to be the equivalent section,so that the true temperature field could be replaced by the temperature field of the equivalent section.Using the average temperature as equivalence criteria,a trapezoidal-parabolic arch superimposed equivalent temperature field model was proposed by simplifying the temperature field curve of the equivalent section.In addition,asimplified average temperature formula,which was noneintegral operation,was deduced from the equivalent temperature field model.The calculation results show that the equivalent temperature field and its average temperature formula are accurate enough. triple-row-pipe freezing;equivalent temperature field;average temperature;frozen soil wall;artificial ground freezing 10.13225/j.cnki.jccs.2013.0166 国家自然科学基金资助项目(50578120,51178336) 胡向东(1961—),男,浙江衢州人,副教授,博士生导师。Tel:021-65988771,E-mail:anton.geotech@tongji.edu.cn。通讯作者:任 辉(1986—),男,湖南常德人,硕士研究生。Tel:021-65985249,E-mail:ren445@126.com TD265.3 A 0253-9993(2014)01-0078-06 胡向东,任 辉.3排管冻结梯形-抛物弓叠合等效温度场模型和平均温度[J].煤炭学报,2014,39(1):78-83. Hu Xiangdong,Ren Hui.A trapezoidal-parabolic arch superimposed equivalent temperature field model and its average temperature formula for triple-row-pipe freezing[J].Journal of China Coal Society,2014,39(1):78-83.doi:10.13225/j.cnki.jccs.2013.0166
Table1Parametervalues
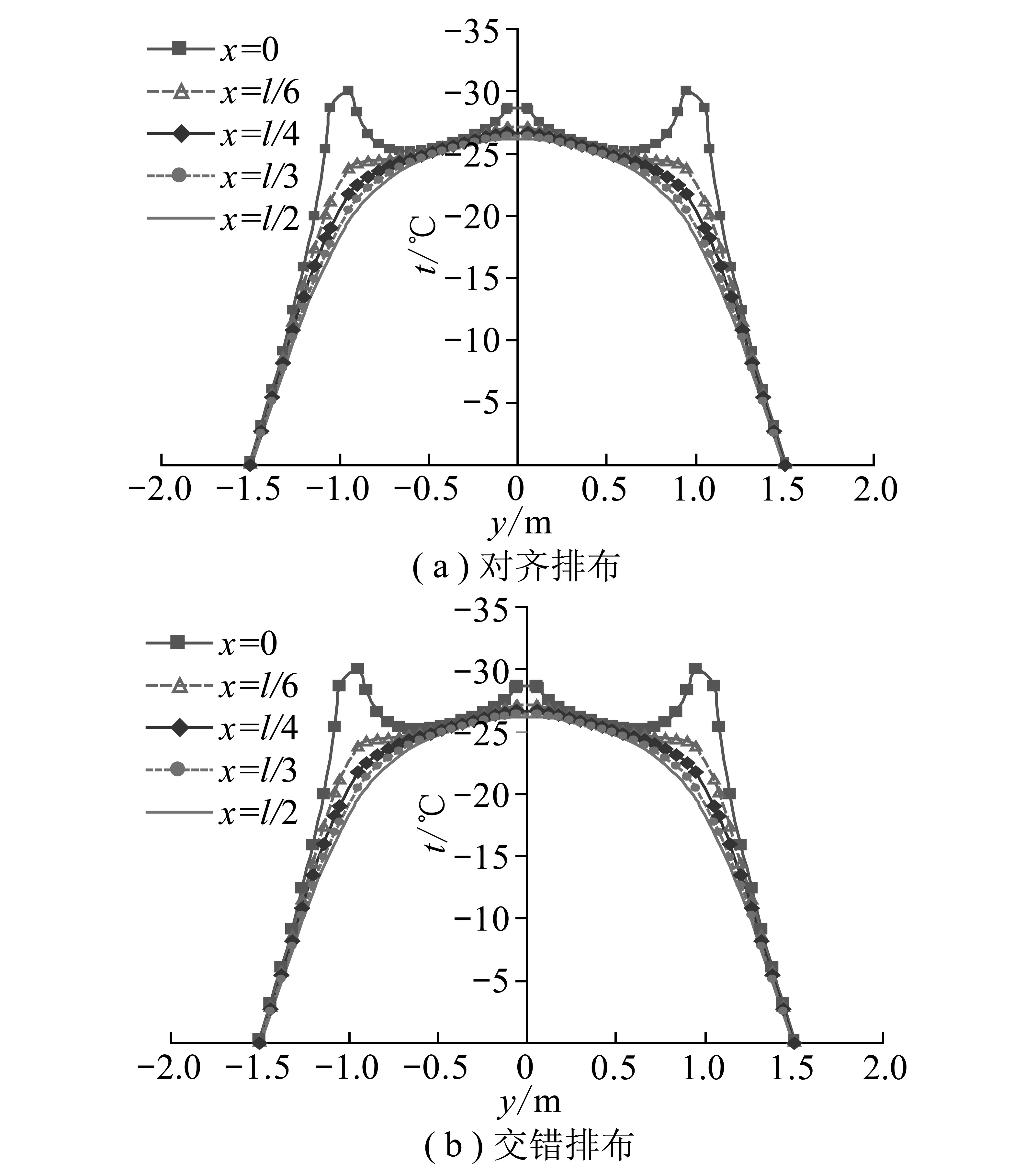
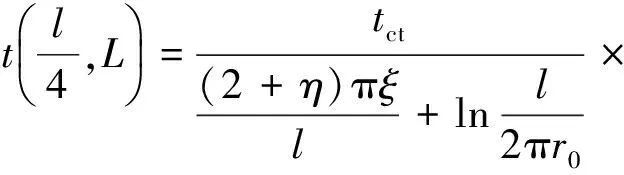
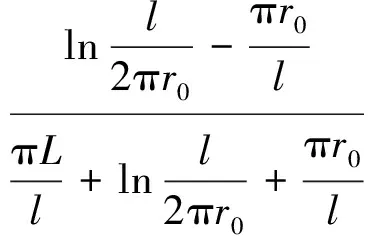







3 利用等效温度场求解平均温度
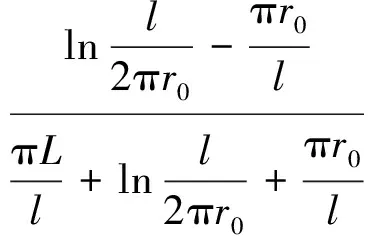

4 结 论


