顶板断裂瞬间煤体稳定性的动力学分析及数值模拟

祝 捷，张 敏,唐 俊，王曌华,谈晓钟

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083；2.中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室，北京 100083)

顶板断裂瞬间煤体稳定性的动力学分析及数值模拟

祝 捷1,2，张 敏1,唐 俊1，王曌华1,谈晓钟2

(1.中国矿业大学(北京) 力学与建筑工程学院，北京 100083；2.中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室，北京 100083)

为了研究顶板突然性断裂诱发煤层失稳的致灾条件，本文采用动力学方法分析了顶板断裂瞬间煤岩系统的受力状态和力学响应。首先推导了顶板断裂时惯性力、惯性力矩的计算公式，进而得到顶板断裂瞬时转动加速度与惯性力、惯性力矩的关系，利用数值模拟计算了顶板断裂前后以及不同转动角加速度条件下的煤岩体应力、变形和两帮位移。计算结果显示：当顶板断裂瞬时转动角加速度较小，即顶板断裂释放能量较小时，工作面煤壁两帮移近量随顶板瞬时转动角加速度的增大而增大；当顶板断裂瞬间转动加速度达到某临界值时，煤岩系统出现失稳分支点，具体体现为工作面处煤体的应力基本不变，煤壁顶部竖向下沉激增，煤岩系统的平衡须依靠煤壁回缩方可维持。因此顶板断裂可以诱发煤岩体系统的失稳，但并非失稳的充分条件。

煤体稳定性；顶板断裂；动力学分析；分岔失稳

冲击地压是采动影响下，达到强度极限的煤岩力学系统将聚集的能量以突然、急剧、猛烈的形式释放出来的动力现象。冲击地压可视作煤岩系统的失稳破坏，分为材料失稳型冲击、结构失稳型冲击和耦合失稳型冲击几种类型[1]。宏细观试验和现场观测结果显示煤中裂纹不断扩展或层裂结构的形成最终促使煤体失稳[2-4]。煤岩冲击失稳与坚硬顶板结构、煤层冲击倾向性、地质构造、不完全开采造成的应力集中等因素有关[5-6]。

将煤层视作受顶底板夹持的积聚能量的变形体，在顶底板与煤层摩擦力作用下维持平衡状态[3]。由于冲击地压的发生能量级别较小，因此需要外在的诱发条件，即扰动促使煤岩体内应力状态产生由静转动的变化[6]。但扰动并不意味着必然发生冲击地压，只有当煤岩系统处于临界稳定状态或接近临界稳定状态时，外界扰动才诱发冲击地压，尤其当煤层处于临界稳定状态时，微小扰动都可能诱发冲击地压。巷道开挖引起的煤岩内部裂纹稳定扩展到不稳定扩展是煤岩应变能快速释放的开端[7-8]；放炮落煤、顶板断裂或断层撕裂引起的动载作用及天然地震引起的震动也可能打破巷道围岩应力平衡导致冲击地压[9]。

顶板断裂是诱发冲击地压的重要因素，学者们建立了坚硬顶板断裂的弹性力学模型[10]、弹性薄板小挠度力学模型[11]和顶板断裂突变模型[12]等，分析工作面上覆坚硬岩层的应力分布、极限垮落步距、工作面前方煤岩能量积聚释放规律以及坚硬顶板断裂起动过程的突变条件。笔者从顶板断裂瞬间的煤岩体受力状态入手，结合数值模拟分析顶板断裂瞬间煤层应力和变形状态的改变，进而研究顶板断裂时煤岩系统的稳定性问题。

1 顶板断裂瞬间的理论分析

煤层开采后，坚硬顶板将悬露、下沉，当其悬露到一定极限跨度后，岩体内应力超过其抗拉强度时，将形成初次断裂。随着推采，顶板岩层形成“砌体梁”结构，发生周期性断裂[10]。图1是工作面前方顶板断裂前后煤岩结构示意图。以往顶板断裂模型采用了不同的边界约束，如弹性地基梁约束、两边简支或一边简支、一边固定等，对顶板内力和弹性能进行了计算，但以静力分析为主。

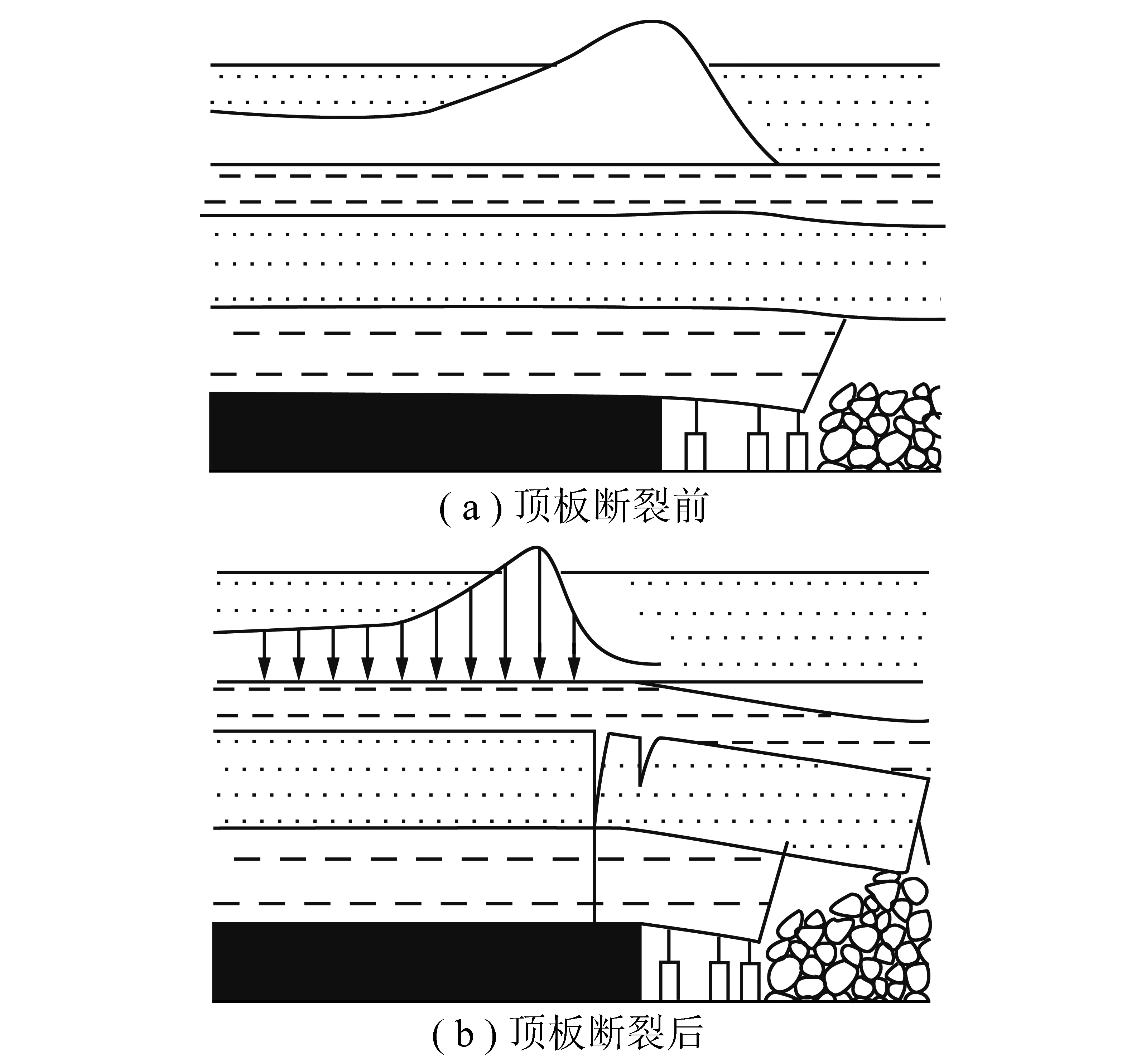
图1 顶板断裂前后煤岩结构示意Fig.1 Coal-rock system before and after roof fracture

为了反映顶板断裂瞬间的情况，笔者利用动力学分析中的动静法对顶板断裂瞬间煤岩系统受力状态进行分析。顶板未断裂时，煤岩系统处于稳定平衡状态，顶板各处转角连续(图1(a))。由于岩层中的原生节理、裂隙以及由于巷道开挖生成次生裂纹的影响，断裂可能出现高应力区或初始缺陷处。假设顶板断裂位置距煤壁x1(图2(a))。

图2 顶板断裂瞬间的力学模型Fig.2 Mechanical model when roof fracturing

笔者根据刚化原理，取图2(b)所示断裂点A后方顶板任意长度(x2-x1)的AB段进行受力分析。AB段顶板长度为(x2-x1)，顶板厚度为H。顶板受垂直应力q及切应力p作用，断裂发生时，A点后方岩梁将做定轴转动，断裂瞬间其角速度为0，转动加速度α。故其惯性力系可简化为作用于断裂处A点惯性力FI和惯性力偶矩MI，即

(1)

(2)

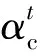
根据动力学的动静法原理，作用于岩梁上所有的主动力、约束力和惯性力组成平衡力系，得到A处岩梁的轴力NAx、剪力VAx和弯矩MBx为

(3)

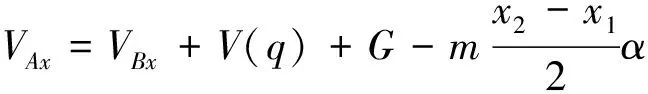
(5)

式中，N(p)，V(q)，M(q)分别是切应力p和垂直应力q在A点处产生的轴力、剪力和弯矩；NBx，VBx，MBx分别为B点轴力、剪力和弯矩；G为AB段顶板自重。如果顶板不断裂，那么A处惯性力FI和惯性力偶矩MI均为0。由式(3)～(5)可知，顶板的断裂瞬间，A处轴力没有变化，A处剪力和弯矩在惯性力和惯性力矩作用下变化如下：

(6)

(7)

式中，ΔVx和ΔMx为顶板断裂在A点引起的附加剪力和附加弯矩，其大小与顶板悬露长度、断裂点位置、转动岩梁自重及转动加速度有关。顶板悬露长度增大、断裂点靠近煤壁、转动岩梁自重增大及转动加速度的提高，都使断裂处附加剪力和附加弯矩加大。

可见顶板断裂改变了煤岩体的受力状态。煤层受到顶底板的夹持，承受很高的压力，煤岩体内储存了大量弹性能。顶板造成的局部剪力和弯矩变化一旦引起顶底板夹持作用减弱或工作面煤体失稳，煤岩体储存的弹性能瞬间释放，极有可能形成突然的煤层冲击破坏。

2 顶板断裂影响的数值计算

2.1 数值模型及计算方案

在理论分析的基础上，笔者通过数值模拟进一步探讨顶板断裂瞬间煤岩体的稳定性问题，采用ANSYS建立二维计算模型如图3所示(x轴正方向朝右，y轴正方向朝上)。

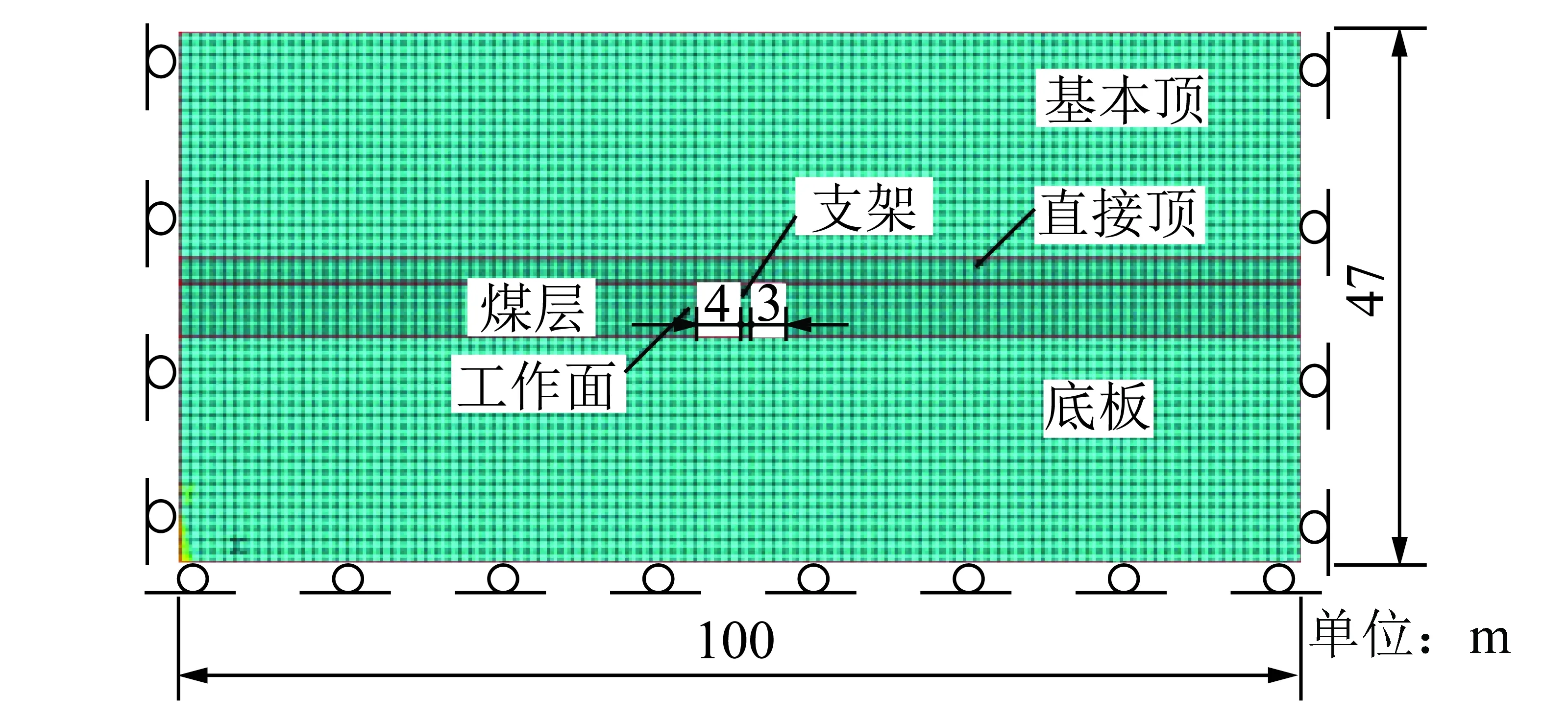
图3 计算模型Fig.3 Numerical model

模型宽100 m，高47 m，单元总数为5 400个，节点数为5 500个，模型上边界为自由边界，施加竖向载荷模拟上覆岩层自重，下边界限制垂直移动，左右边界限制水平移动。模拟开采深度600 m，在模型上边界受10 MPa垂直应力，水平方向受位移约束。煤层开切眼巷道宽度8 m，支架宽度1 m，距离工作面4 m。计算时采用Mohr-Coulomb强度准则作为煤岩体材料屈服判据。根据岩石力学实验和现场调研资料，数值计算中各岩层参数取值见表1。

表1模型中的材料力学参数
Table1Themodelparametersofrockandcoal

材料密度/(kg·m-3)弹性模量/GPa泊松比黏聚力/MPa内摩擦角/(°)基本顶270720 850 195 229 5直接顶24618 800 264 430 0煤层14403 400 162 426 9底板287317 660 146 529 2支架7800210 000 30

2.2 顶板断裂前的计算结果

首先对顶板断裂前，即上覆岩层作用的载荷工况下进行求解。考虑实际煤层的变形特点，求解调用非线性大变形计算模式，得到顶板断裂前煤岩体应力和变形情况如图4所示。图4显示工作面前方10 m形成垂直应力集中区；工作面前方1.7 m内煤体朝巷道方向产生水平位移，煤壁处最大水平位移为2.5 mm。

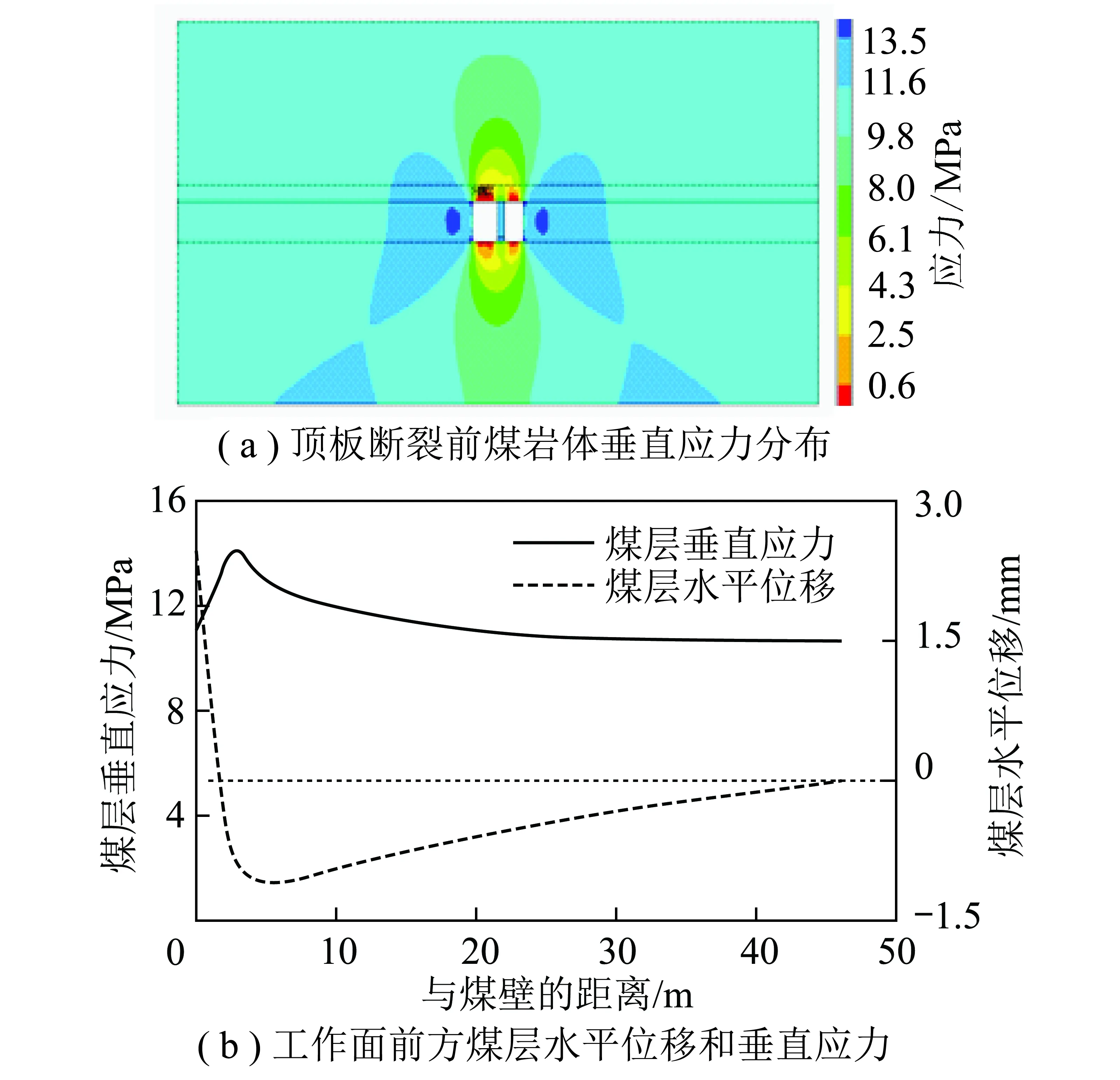
图4 顶板断裂前煤岩体的位移和应力Fig.4 The horizontal displacement and vertical stress of coal beam at front of the working face

基于节点应力的计算结果，得到开切眼巷道上方直接顶的弯矩分布如图5所示。支架上方顶板弯矩较小。巷道两个顶角上方直接顶弯矩最大，达到5 973 kN·m；距巷道顶角2 m处岩梁弯矩较大，达到3 965 kN·m。因此初步拟定顶板断裂位置在距工作面水平距离2 m处。

图5 顶板断裂前直接顶的弯矩Fig.5 The bending moment of floor before fracture

2.3 顶板断裂瞬间的计算结果

如图2(a)所示，一旦工作面煤壁上方顶板发生断裂，断裂处后方岩梁随即产生角加速度。依据式(6)和(7)，角加速度决定了惯性力和惯性力矩的大小，角加速度越大，断裂瞬间的惯性力和惯性力矩越大，对煤岩系统的影响也越大。笔者在工作面上方顶板施加惯性力和惯性力矩，同时在巷道煤壁上设置测点1和测点2(图6)。

图6 惯性力施加情况和测点位置Fig.6 The inertial forces and gauging points

在2.2节计算基础上，笔者对不同惯性角加速度条件下的煤层力学响应，包括应力、变形和煤壁水平位移进行了计算。为了便于观察顶板断裂对煤体位移的影响，笔者将未断裂时测点位移置零。

表2列出了不同惯性角加速度对应测点1的竖向应力σy和竖向位移uy。由表2可知，对应未断裂前测点1的应力(α=0)，顶板断裂对测点1竖向应力的影响较小。但是对比顶板角加速度α为19 r/s2和19.5 r/s2的计算结果发现：α=19.5 r/s2时，应力几乎不变，但竖向位移显著增大。测点1的垂直位移如图7所示。图中测点1的竖向位移随断裂瞬间顶板转动角加速度的增大而增大；顶板角加速度19.5 r/s2时，测点位移曲线出现偏折，即煤壁顶部竖向位移激增。

表2不同转动加速度下的竖向应力和位移(测点1)
Table2Theverticalstressanddisplacement(PointNo.1)

α/(r·s-2)σy/MPauy/mm015 2902 515 310 0295 015 320 0587 515 340 08710 015 350 11612 515 370 14515 015 380 17417 515 400 20319 015 4080 22319 515 4090 252

图7 不同角加速度下的测点垂直位移Fig.7 The vertical displacement of Points No.1

3 讨 论

测点1竖向应力的最大增幅(α=19.5 r/s2时)仅为7.8%，因此本文施加的惯性力和惯性力矩与煤岩系统原有载荷相比甚小，顶板断裂影响可视为微小干扰。依据平衡稳定性的根本准则，对处于平衡状态的体系施加微小干扰，如果扰动后的状态对原始状态的偏离在允许范围以内，那么煤岩系统是稳定的，否则是不稳定的。

当断裂引起的角加速度α=19.5 r/s2时，测点1出现应力基本不变时竖向位移激增的现象具有结构失稳特征。对应表1不同角加速度，作者通过数值计算得到图6测点2，即煤壁中部水平位移(图8)。图8显示断裂瞬时角加速度α≤19.0 r/s2时，煤壁水平位移随着转动角加速度的增大而增大，且煤壁位移始终朝巷道方向；当α=19.5 r/s2时，煤壁水平位移骤然减小为负值，这意味着煤壁需要向工作面前方回缩一定距离后，煤岩系统方可维持平衡。

上述现象可以用结构失稳理论加以解释，即α=19.5 r/s2时的煤岩系统平衡状态虽然在α=19.0 r/s2的平衡状态附近，但α=19.5 r/s2时煤岩平衡系统煤壁变形出现回缩的突然转变，其煤岩体变形和应力状态与α≤19.0 r/s2时已有本质不同。依据本文计算结果，α=19.0 r/s2成为失稳分支点。顶板断裂瞬间，顶板转动角加速度α大于19.0 r/s2时，煤层即发生分岔失稳。

图8 不同角加速度下的煤壁中部水平位移Fig.8 The inertial forces and gauging points

4 结 论

(1)采用动力学动静法分析了顶板断裂瞬间煤岩系统的受力状态，推导了顶板断裂时惯性力和惯性力矩的计算公式，得到顶板瞬时转动加速度与惯性力和惯性力矩的关系。

(2)基于顶板断裂惯性力和惯性力矩的理论分析，模拟分析了顶板断裂前后以及不同惯性角加速度条件下的煤岩体应力和变形，计算结果显示：当顶板断裂瞬时转动角加速度较小时，工作面煤壁位移随顶板转动角加速度的增大而增大；当顶板断裂瞬间转动加速度达到某临界值，煤壁顶部竖向位移激增，煤壁两帮的变形由指向工作面突变为背离工作面。

(3)依据结构稳定性原理，本文算例中的煤层在顶板断裂瞬间转动加速度为19.5 r/s2时发生失稳，而顶板转动加速度较低时煤层可保持稳定。由此可见顶板断裂不一定诱发煤层失稳，煤岩系统受扰动前的力学状态和顶板断裂时释放的能量都会对煤体稳定性产生重要作用。

[1] 姜耀东，赵毅鑫，刘文岗，等.煤岩冲击失稳的机理和实验研究[M].北京：科学出版社，2009:2-27.

[2] 张晓春，缪协兴，杨挺青.冲击矿压的层裂板模型及实验研究[J].岩石力学与工程学报，1999，18(5)：506-510. Zhang Xiaochun，Miao Xiexing，Yang Tingqing.The layer-crack-plate model and testing study of the rockburst in mines[J].Chinese Journal of Rock Mechanics and Engineering，1999，18(5)：506-510.

[3] 赵毅鑫，姜耀东，韩志茹.冲击倾向性煤体破坏过程声热效应的试验研究[J].岩石力学与工程学报，2007，26(5)：965-971. Zhao Yixin,Jiang Yaodong,Han Zhiru.Experimental study on acoustic and thermal infrared characteristics of bump-phone coal[J].Chinese Journal of Rock Mechanics and Engineering,2007，26(5)：965-971.

[4] 尹光志，代高飞，皮文丽，等.冲击地压的滑块模型研究[J].岩土力学，2005，26(3)：359-364. Yin Guangzhi，Dai Gaofei，Pi Wenli，et al.Study on rock burst using stick slip model[J].Rock and Soil Mechanics，2005，26(3)：359-364.

[5] 窦林名,曹胜根,刘贞堂,等.三河尖煤矿坚硬顶板对冲击矿压的影响分析[J].中国矿业大学学报，2003，32(4)：388-392. Dou Linming，Cao Shenggen，Liu Zhentang，et al.Influence of key roof on rock burst in Sanhejian Mine[J].Journal of China University of Mining & Technology，2003，32(4)：388-392.

[6] 邹德蕴，姜福兴.煤岩体中储存能量与冲击地压孕育机理及预测方法的研究[J].煤炭学报，2004，29(2)：159-162. Zou Deyun,Jiang Fuxing.Research of energy storing and gestation mechanism and forecasting of rockburst in the coal and rock mass[J].Journal of China Coal Society，2004，29(2)：159-162.

[7] 潘一山，李忠华，章梦涛.我国冲击地压分布、类型、机理及防治研究[J].岩石力学与工程学报，2003，22(11)：1844-1851. Pan Yishan，Li Zhonghua，Zhang Mengtao.Distribution，type，mechanism and prevention of rockbrust in China[J].Chinese Journal of Rock Mechanics and Engineering,2003，22(11)：1844-1851.

[8] 缪协兴，安里千，翟明华，等.岩(煤)壁中滑移裂纹扩展的冲击矿压模型[J].中国矿业大学学报，1999，28(2)：113-117. Miao Xiexing，An Liqian，Zhai Minghua，et al.Model of rockburst for extension of slip fracture in palisades[J].Journal of China University of Mining & Technology，1999，28(2)：113-117.

[9] 齐庆新，刘天泉，史元伟.冲击地压的摩擦滑动失稳机理[J].矿山压力与顶板管理，1995(4)：174-177. Qi Qingxin，Liu Tianquan，Shi Yuanwei. Mechanism of frction sliding destability of rock burst[J]. Ground Preesure and Strata Control，1995(4):174-177.

[10] 李新元，马念杰，钟亚平,等.坚硬顶板断裂过程中弹性能量积聚与释放的分布规律[J].岩石力学与工程学报,2007,26(S1):2786-2793. Li Xinyuan，Ma Nianjie，Zhong Yaping,et al.Storage and release regular of elastic energy distribution in tight roof fracture[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(S1):2786-2793.

[11] 姜福兴.薄板力学解在坚硬顶板采场的适用范围[J].西安科技大学学报,1991(2):12-19. Jiang Fuxing.Application range of thin plate mechanics solution in hard roof of working face[J].Journal of Xi’an University of Science and Technology,1991(2):12-19.

[12] 王 平，姜福兴，冯增强,等.高位厚硬顶板断裂与矿震预测的关系探讨[J].岩土工程学报,2011,33(4):618-623. Wang Ping,Jiang Fuxing,Feng Zengqiang,et al.Relationship between fracture of high-position thick and hard roof and mine quake forecast[J].Chinese Journal of Geotechnical Engineering,2011,33(4):618-623.

Dynamicsanalysisandnumericalsimulationoncoalstabilityatthemomentofrooffracture

ZHU Jie1,2，ZHANG Min1,TANG Jun1,WANG Zhao-hua1,TAN Xiao-zhong2

(1.SchoolofMechanics&CivilEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China;2.StateKeyLabofCoalResourcesandSafeMining(Beijing),ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China)

The stress state and mechanical responses of coal and rock system at the moment of roof fracture were analyzed to investigate the disaster mechanism of coalburst due to roof fracture by means of the dynamic methods.And the inertial force and moment were deduced.Based on the relationship of the inertial force,moment and roof rotational acceleration,the stress,deformation and displacement of coal-rock mass before and after fracture,including different inertial angular acceleration conditions were simulated.The numerical results indicate that when roof rotational acceleration and its release energy is low,coal wall by the side of working face moves to roadway and its shift increases with roof rotational acceleration increasing.Once the inertial angular acceleration reaches a critical value,the bifurcation instability point occurs.The coal-rock system keeps stable only when coal wall retracts.Meanwhile the top of coal wall sink sharply though the stress is almost invariant.Therefore roof can course the instability of coal-rock system,but not a sufficient condition for coalburst.

coal stability;roof fracture;dynamics analysis;bifurcation instability

10.13225/j.cnki.jccs.2013.0008

国家重点基础研究发展计划(973)资助项目(2010CB226801);中国矿业大学煤炭资源与安全开采国家重点实验室开放基金资助项目(SKLCRSM10KFB09);高等学校博士学科点专项科研基金资助项目(20120023120011)

祝 捷(1978—)，女，江西南昌人，副教授。Tel：010-62339322，E-mail:chinazhujie@163.com

TD315

A

0253-9993(2014)02-0253-05

祝 捷，张 敏,唐 俊,等.顶板断裂瞬间煤体稳定性的动力学分析及数值模拟[J].煤炭学报,2014,39(2):253-257.

Zhu Jie，Zhang Min,Tang Jun,et al.Dynamics analysis and numerical simulation on coal stability at the moment of roof fracture[J].Journal of China Coal Society,2014,39(2):253-257.doi:10.13225/j.cnki.jccs.2013.0008