一类线性双曲型偏微分方程的有限差分格式求解

刘付军，龚 东，王高放

(河南工程学院 理学院，河南 郑州451191)

有限差分法是求解微分方程的一种有效的数值解法．对于线性双曲型偏微分方程，已建立了一些典型差分格式，如显式、隐式和紧差分格式等［1-4］．文献［5］利用差分格式对二阶常微分方程进行了求解．文献［6］利用一种加权平均格式对一阶双曲型偏微分方程进行了数值分析．双曲型偏微分方程是描述振动或波动现象的一类重要的偏微分方程，在实际问题中有着广泛的应用［7］．针对二阶常系数线性双曲型偏微分方程建立了两种差分格式并对这两种差分格式进行加权平均，求出加权平均值，建立了一个新的差分格式，验证了该差分格式解的存在性、收敛性和稳定性．

1 差分格式的建立

考虑二阶双曲型问题

区域记作Ω={(x，t)|0≤x≤1，0＜t≤T}．

对区域Ω进行剖分．记xi=ih，0≤i≤m;tk=kτ，0≤k≤n．其中，h=1/m，τ=T/n．记Ωh={xi|0≤i≤m}，Ωτ={tk|0≤k≤n}，Ωhτ=Ωh×Ωτ．称在t=tk上的节点{(xi，tk)|0≤i≤m}为第k层节点．定义Ωhτ上的网格函数用来表示，其中．此外，记，0≤i≤m，0≤k≤n．

1．1 显式差分格式

在节点(xi，tk)上考虑定解问题(1)，有

将u(xi-1，tk)和u(xi+1，tk)分别在节点(xi，tk)处进行Taylor展开，得到

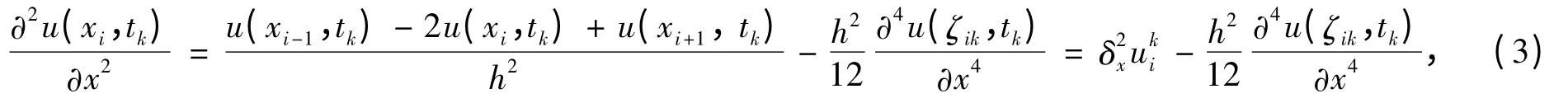
其中，xi-1＜ζik＜xi+1．将u(xi，tk-1)和u(xi，tk+1)分别在节点(xi，tk)处进行Taylor展开，得到

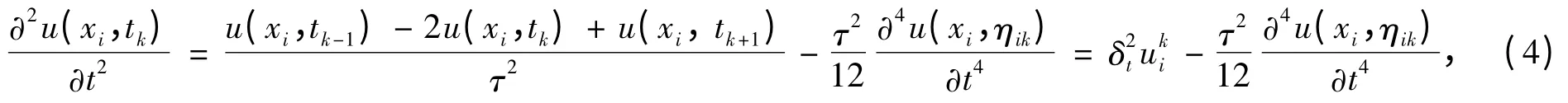
其中，tk-1＜ηik＜tk+1．将式(3)和式(4)代入式(2)得到

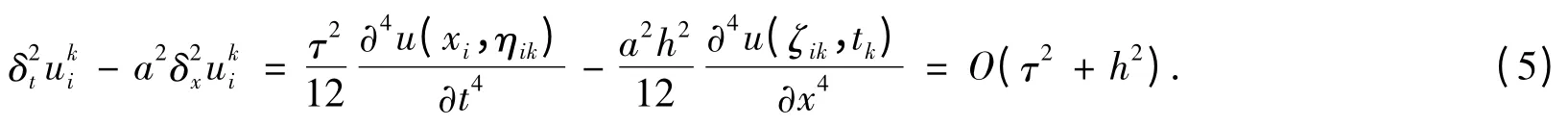
针对问题(1)，建立如下近似差分格式:

该格式称为3层5点显式差分格式．

1．2 隐式差分格式

将u(xi，tk-1)和u(xi，tk+1)分别在节点(xi，tk)处进行Taylor展开，得

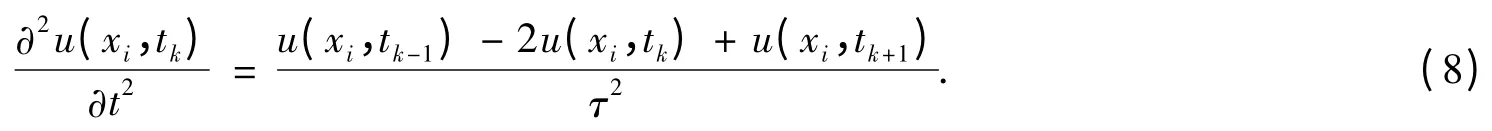
将式(7)和式(8)代入到式(2)中，可得如下近似差分格式:

该格式称为3层5点的隐式差分格式．

1．3 加权平均差分格式

对显格式(6)和隐格式(9)进行加权平均，加权平均数用θ表示，得到

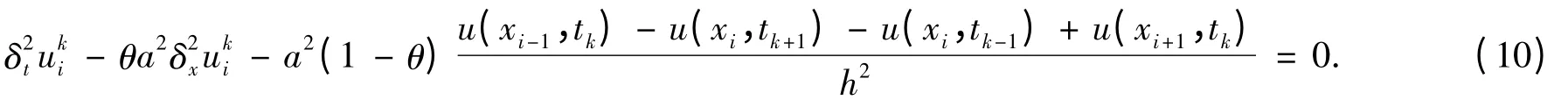
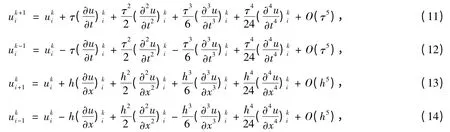
其截断误差记为

将式(11)至式(14)代入式(10)，可得

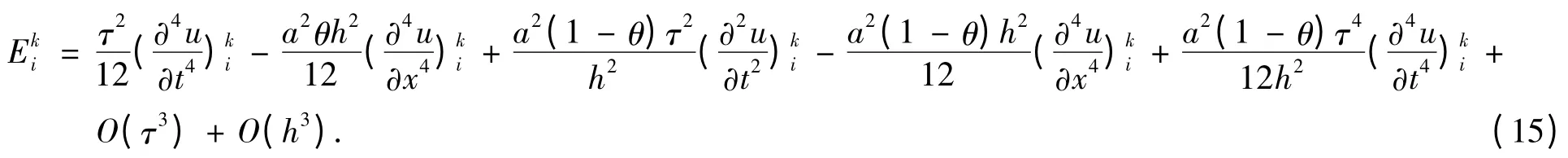
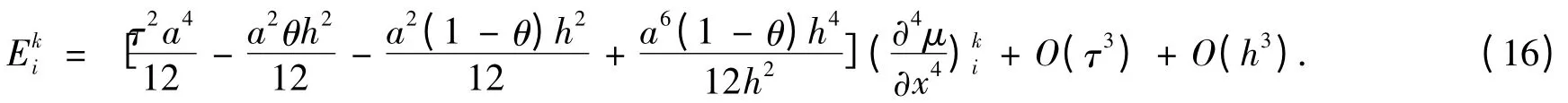
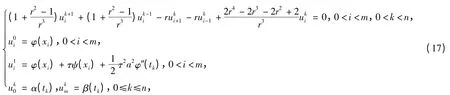
该格式称为一种新的加权平均差分格式．

2 加权平均差分格式解的收敛性和稳定性

首先，得到该加权平均差分格式解的存在性．

定理1 加权平均差分格式(17)的解是存在唯一的．

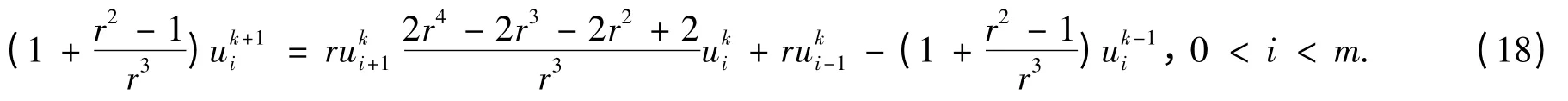
下面给出该加权平均差分格式解的收敛性和稳定性．

定理2 加权平均差分格式(17)的解是收敛的．

证明 设{u(x，t)|0≤x≤1，0≤t≤T}是定解问题(1)的解是差分格式(17)的解．记，0≤i≤m，0≤k≤n，则由式(16)可知，当h，τ→0时，误差e(h3+τ3)→0，差分格式(17)的解收敛到定解问题的精确解，则差分格式(17)与相应的微分方程(1)相容，故该差分格式是收敛的且差分格式具有三阶精度．

定理3 加权平均差分格式(17)的解是稳定的．

证明 Lax定理指出，对于一个适当提出的线性微分方程初值问题以及它的一个满足相容性条件的差分逼近，收敛性的充分必要条件是稳定性．

根据前面已经证明了的差分格式(17)的相容性和收敛性，由Lax定理即可得差分格式(17)的稳定性．

3 数值算例

应用新的加权平均差分格式(17)计算如下定解问题:

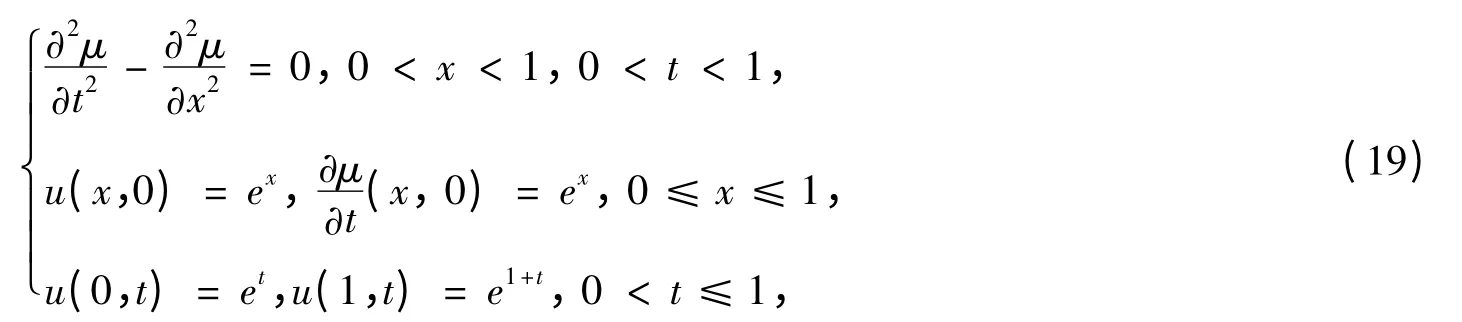
该定解问题的精确解为u(x，t)=ex+t．

下面给出了当步长h=1/10，τ=1/20(即步长比r=1/2)时，计算得到的部分数值结果，如表1所示．

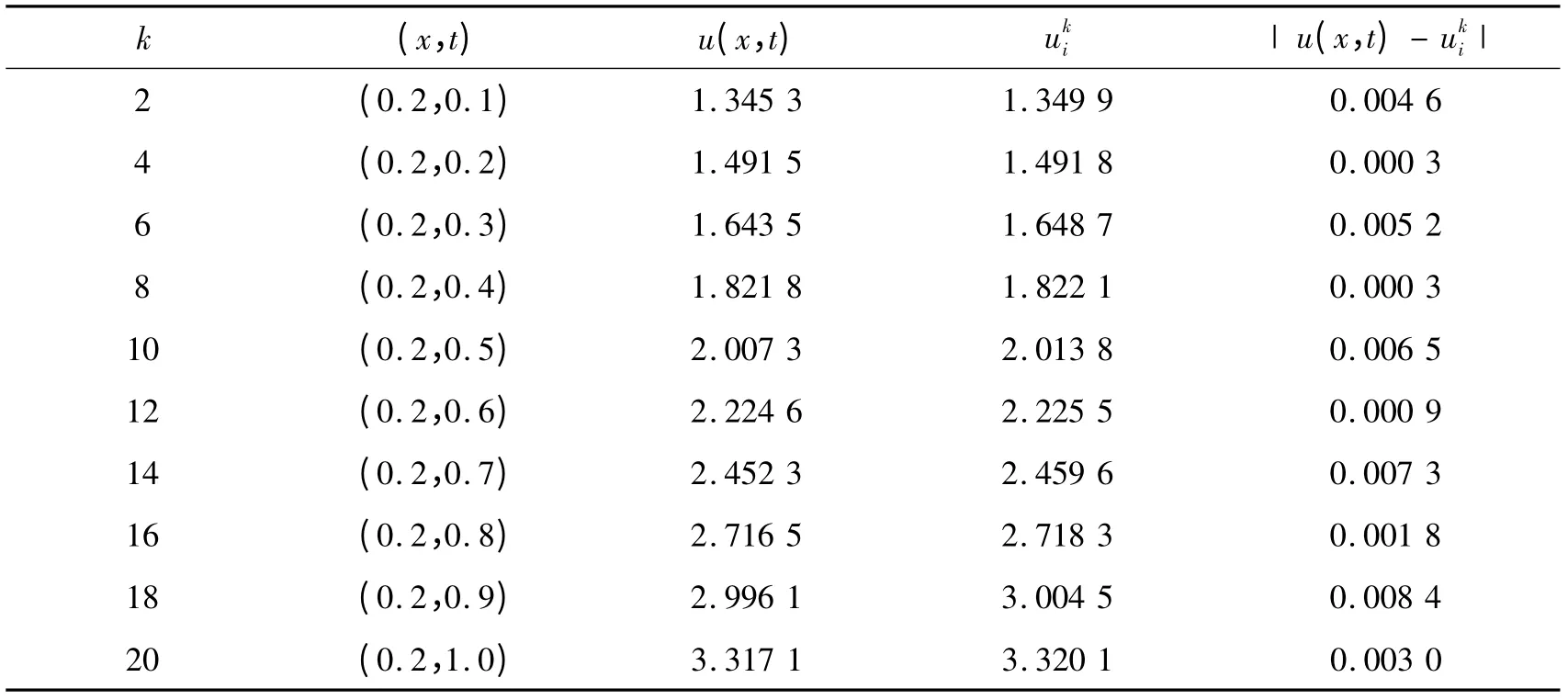
表1 数值解与精确解的比较Tab．1 Comparison of the numerical solution and the exact solution

由表1可以看出，精确解与数值解的误差控制在量级范围之内，且当h，τ→0时，所得的结果越接近精确解．

［1］ 李立康．微分方程数值解法［M］．上海:复旦大学出版社，2003．

［2］ 孙志忠．偏微分方程数值解法［M］．北京:科学出版社，2012．

［3］ 胡建伟，汤怀民．微分方程数值方法［M］．北京:科学出版社，2007．

［4］ 李胜坤，冯民富，李珊．Benjamin-Bona-Mahony方程的有限差分近似解［J］．四川师范大学学报:自然科学版，2003，26(4):363-365．

［5］ 张守贵．用差分法求解二阶常微分方程初值问题［J］．重庆理工大学学报:自然科学版，2012，26(8):110-112．

［6］ 杨韧．求解一阶线性双曲型偏微分方程组的一个差分格式［J］．四川师范大学学报:自然科学版，2009，32(5):614-617．

［7］ 谷超豪，李大潜，陈恕行，等．数学物理方程［M］．北京:高等教育出版社，2002．