The Application of BP Neural Network Based on PSO Algorithm to Pressure Sensor Temperature Compensation*

SUN Yanmei，MIAO Fengjuan，TAO Bairui

(University of Qiqihar Institute of Communications and Electronics Engineering，Qiqihar Heilongjiang 161006，China)

The Application of BP Neural Network Based on PSO Algorithm to Pressure Sensor Temperature Compensation*

SUN Yanmei*，MIAO Fengjuan，TAO Bairui

(University of Qiqihar Institute of Communications and Electronics Engineering，Qiqihar Heilongjiang 161006，China)

For the temperature drift of the silicon piezoresistive pressure sensor，compensation method by Back Propagation(BP)network based on Particle Swarm Optimization(PSO)algorithm has been proposed.This model has overcomed the drawback of slow convergence and easily trapping in the local minimum of BP network through global search weight and threshold in PSO algorithm.The simulation experiment results show that the model can depress the temperature drift of the silicon piezoresistive pressure sensor effectively，and the stability and accuracy of the silicon piezoresistive pressure sensor are improved greatly.

temperature compensation;particle swarm optimization algorithm;BP network;pressure sensor

目前，在压力测量领域中，硅压阻式压力传感器是使用最多的一种，由于半导体材料的压阻系数具有较大的温度系数，导致硅压阻式压力传感器的输出极易受到温度的影响，即存在温度漂移问题。温度漂移严重制约着硅压阻式压力传感器的测量精度和应用领域，为消除非目标参量(温度)对压阻式压力传感器输出特性的影响，压阻式压力传感器的温度补偿研究一直在进行［1-6］。

BP神经网络是温度补偿中使用最为广泛的一种，它具有强大的非线性映射能力和自学习能力［6-10］，但由于BP算法的本质是梯度下降法的一种迭代学习，梯度下降法进行稳定学习要求学习率很小，因此使得收敛速度很慢。梯度下降法训练时从某一点开始沿误差函数的斜面逐渐达到最小值，误差函数一般存在多处曲面谷［2］，梯度下降法只能搜索到误差曲面的某一低谷，但无法跳出，也就搜索不到其他更小的误差，即陷入局部极小，而粒子群优化算法通过追随当前搜索到的最优值可进行全局寻优，可以有效的解决BP网络收敛速度慢和易陷入局部极小的问题［11-12］。

1 BP神经网络

BP神经网络属于前向神经网络，其结构示意图如图1所示。

图中，P为输入，R为维数;S1为隐含层神经元个数;S2为输出层神经元个数;W1为隐层神经元权值;

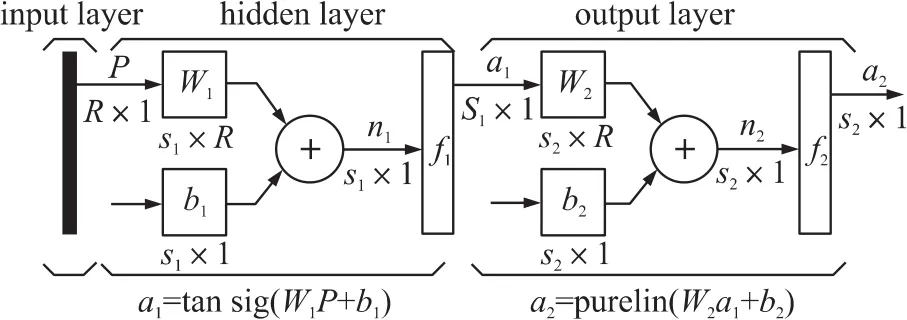
图1BP网络结构示意图

W2为输出层神经元权值;a1为隐层神经元输出［4］;a2为输出层神经元输出;b1为隐层神经元阈值;b2为输出层神经元阈值;n1为隐层节点输入;n2为输出节点输入;f1为传递函数，一般为:f(x)=1/(1+e-x);f2为purelin型传递函数。网络误差为:

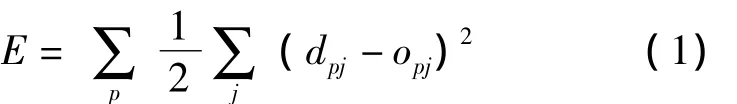
其中，dpj为第p个输入模式输出神经元j的理想输出［8，10］，opj为期望输出。

BP算法权值修正公式为:

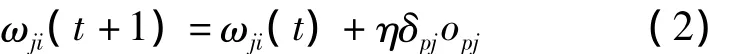
其中，η为学习速率。

输出层神经元:

隐层神经元:

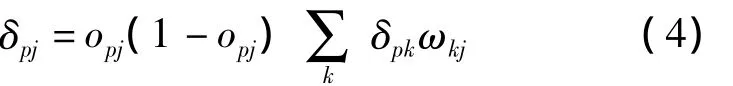
BP算法的本质是梯度下降法的一种迭代学习，梯度下降法进行稳定学习要求学习率很小，因此使得收敛速度很慢。而且训练从某一点开始沿误差函数的斜面逐渐达到误差的最小值，所以起点不同将产生不同的极小值，即得到不同的最优解。

2 基于PSO的BP神经网络温度补偿

2.1粒子群优化算法

粒子群优化算法PSO(Particle Swarm Optimization)是基于群体智能的进化算法技术，此算法采用实数求解，且需要调整的参数较少，易于实现，是一种通用的全局搜索算法［11］。在优化过程中，每个粒子记忆、追随当前的最优粒子，在解空间中进行搜索，粒子群算法初始化为一群随机粒子，然后通过迭代找到最优解。每次迭代，粒子通过追逐两个极值更新自己的位置:一个是粒子自身找到的当前最优解，这个解称为个体极值pbest，另一个是整个群体当前找到的最优解，这个解称为全局极值gbest。粒子在找到上述两个极值后，根据下列式子更新自己的位置。

式中，ω为惯性权重;c1和c2为学习因子;m1、m2为介于(0，1)之间的随机数和分别为粒子i在第k次迭代中第d维的速度和位置，两者都被限定在一定得范围内;是粒子i在第d维的个体极值的位置;是群体在第d维的全局极值的位置。

2.2 基于PSO的BP神经网络温度补偿算法设计和实现

BP网络训练的关键是权阈值的更新过程，PSO搜索过程主要是不同维数上速度和位置的改变，因此BP网络中的权阈值应与PSO中粒子的位置相对应。每个粒子代表一组待优化的权阈值。神经网络的训练目标是使样本输出值与网络实际输出值的误差平方和达到最小(对应的PSO中的适应值最大)，适应度函数取为:

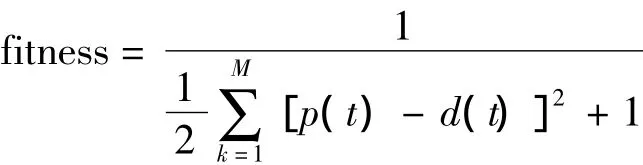
其中，M为学习样本数，p(t)为网络的实际输出，d(t)为样本输出。

PSO需要优化的连接权值总个数为:M=m× (n+1)+m+1，n为输入层神经元节点数，m为隐层神经元节点数。用PSO算法优化的权值和阈值作为BP网络的初始权值和阈值，然后构建BP网络进行训练［12］。

2.3 算法实现步骤

①对输入数据进行标准化处理;②将数据分为测试数据和训练数据;③初始化BP网络结构，设定输入层、隐层、输出层的神经元个数;④初始化粒子群及每个粒子速度;⑤计算每个粒子的适应度:输入一个粒子，按BP网络的前向计算方法计算出每个粒子的输出值及其均方误差;再计算出所有样本的均方差，计算该粒子的适应度。继续输入其他粒子，计算出所有粒子的适应度;⑥比较适应度，确定每个粒子的个体极值点和全局最优极值点:若present＞pbest，pbest= present，则pbest=present;否则，pbest不变;若present＞gbest，则gbest=present;否则，gbest不变;⑦更新每个粒子的位置和速度，判断更新后的速度和位置是否在限定的范围内。1)考虑速度时，若vij＞vmax，则vij=vmax，否则vij不变;2)考虑位置时，若xij＜xmin，则xij=xmax，否则xij不变。其中vmax，xmin都为常数;⑧迭代次数若达到最大迭代次数或k与k+1次迭代过程中的全局最优极值的绝对差值abs(gbest(k+1)-gbest(k))低于设定的最小误差，则迭代过程结束。算法收敛时最后一次迭代的全局最优值gbest中每一维的权值和阈值就是所求的;否则返回(4);⑨将PSO优化好的权值和阈值作为BP网络的初始权值和阈值对网络进行训练;⑩将测试数据代入训练好的网络进行仿真。

3 压力传感器温度补偿

3.1 压力传感器温度漂移标定数据

实验采用MPX10型压力传感器，把压力传感器和温度传感器放在恒温箱中，温度分别为22℃、34℃、44和70℃共4个温度点，然后测量出不同温度下不同压力标定值的压力传感器电压输出值。压力标定值为P，传感器的输出电压为Up，工作温度由集成温度传感器AD590测定，其输出为Ut，其标定数据如表1所示。3.2温度补偿

将基于PSO的BP神经网络温度补偿模型用于补偿该压力传感器，将Up和Ut作为网络输入，标定值p作为网络输出值，对数据做归一化处理，在MATLAB中用premnmx函数可实现标准化，标准化后所得样本库数据如表2所示。

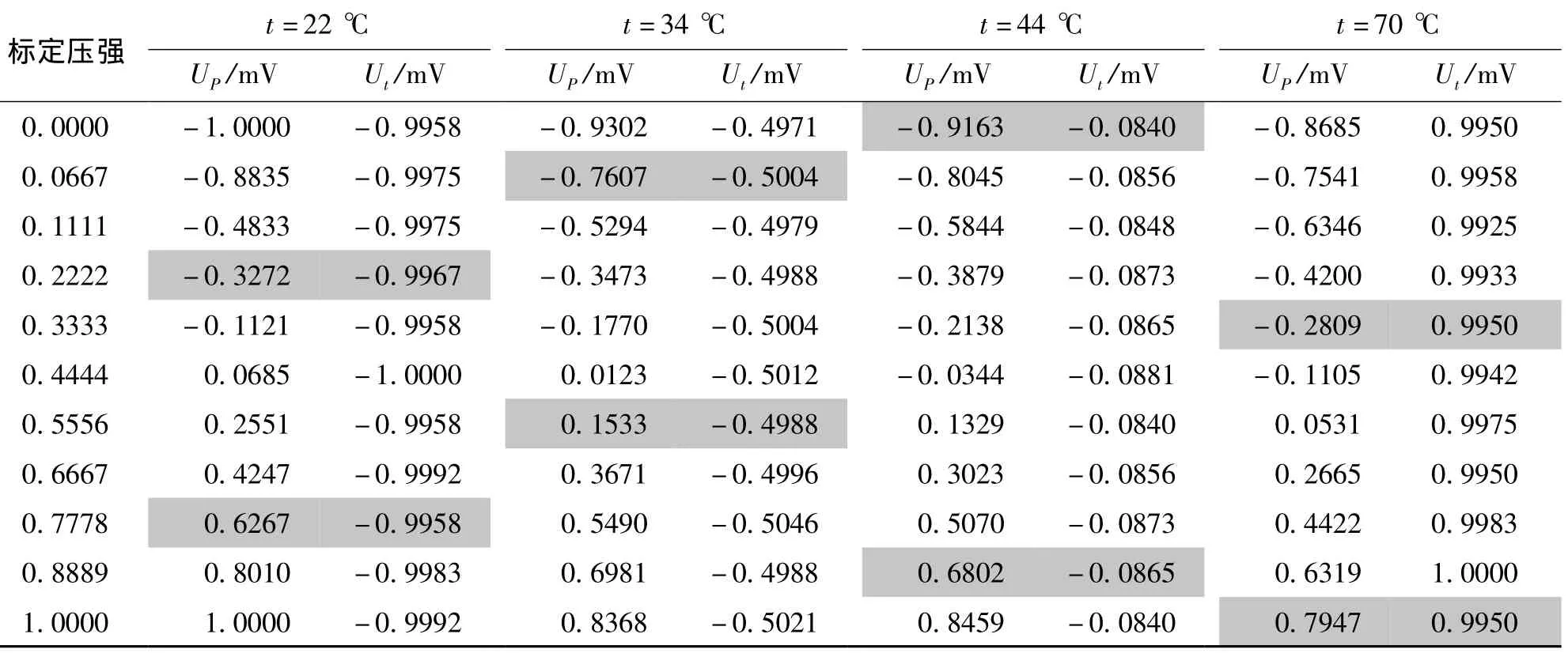
表2 标准化后的标定数据

按照§2.3所述步骤进行温度补偿，建立单隐层BP网络模型:2个输入节点和1个输出节点，隐层节点确定为11个，隐含层使用Sigmoid函数，输出层的计算使用线性Pureline函数;最大迭代次数设为1 500;目标误差设为1×10-6;训练函数为trainlm;学习速率为0.01;学习函数为learngdm;PSO算法中初始搜索点的位置及其速度在允许的范围内随机产生;种群规模为40;惯性权重取1;学习因子c1=c2=2.5;将样本库表2中32组数据进行网络训练。其余8组作为测试样本(阴影部分)。

PSO寻优结束后相应的权值矩阵和阈值矩阵分别为:

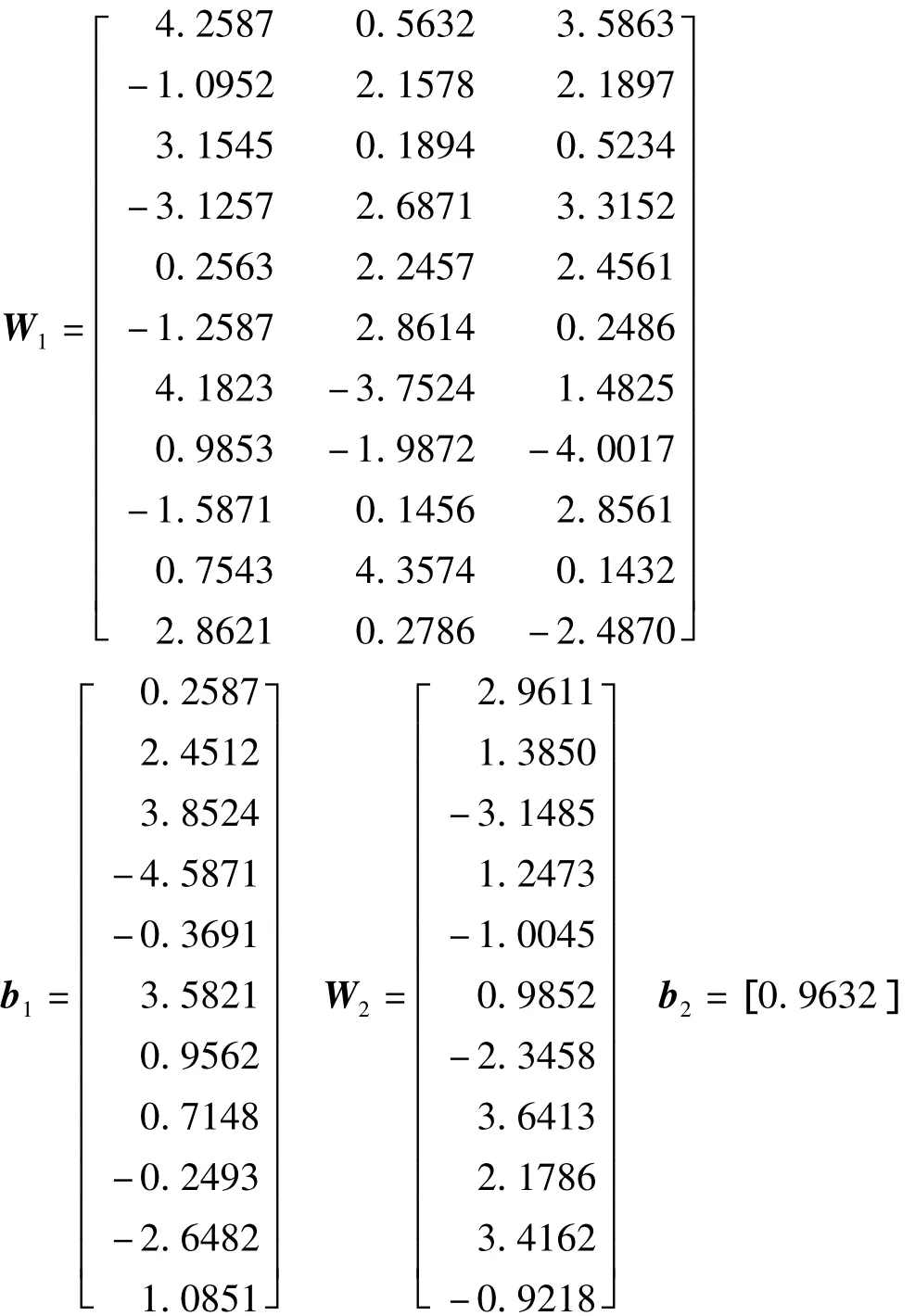
将PSO优化好的权值和阈值作为BP网络的初始权值和阈值对网络进行训练，经过50次迭代后，目标误差达到1.2539×10-6，如图2(a)所示。同样的数据用BP网络进行训练，经过50次迭代后，训练误差为1.9827×10-4，其训练曲线如图2(b)所示，其目标误差同样为10-6由此可知，BP网络陷入了局部极小。

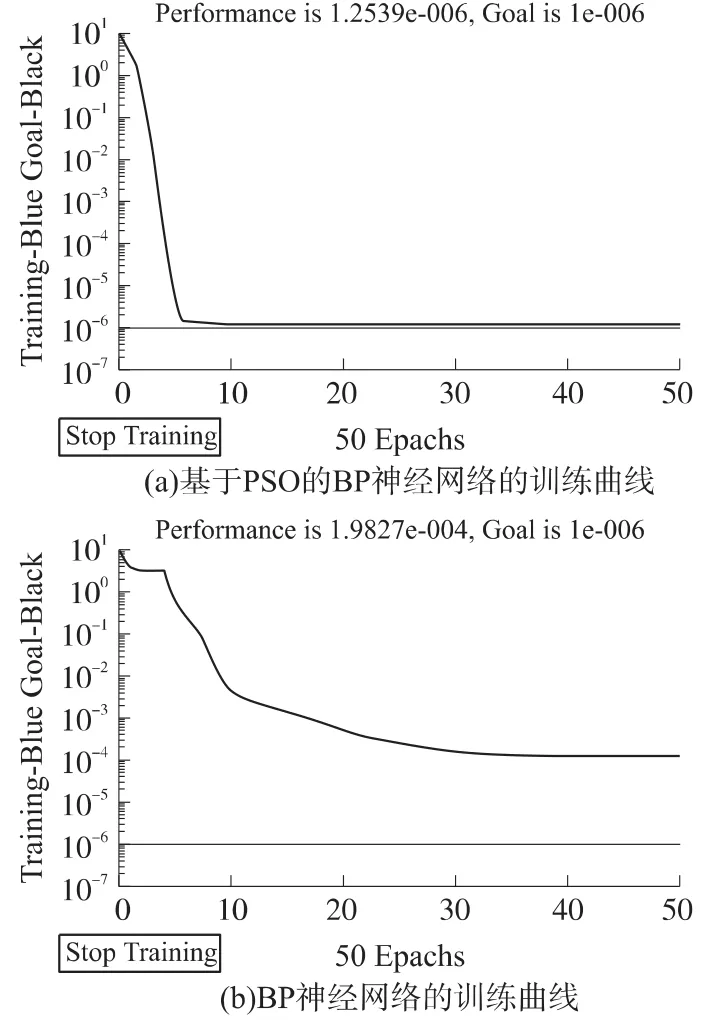
图2 训练曲线

可以看出，与BP网络相比，基于PSO的BP神经网络收敛速度更快，而且补偿精度高，有效避免了局部极小。将测试样本代入训练好的网络，温度补偿后的压力输出值，如表3所示。

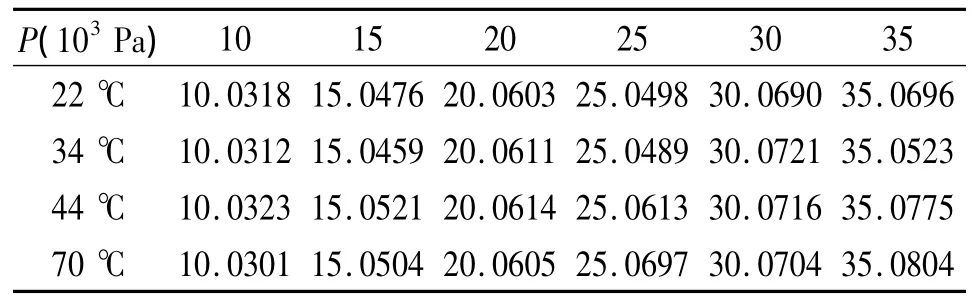
表3 基于PSO的BP神经网络的补偿数据

3.3 补偿效果及分析

基于PSO的BP神经网络与BP神经网络温度漂移补偿过程对比如图3所示。

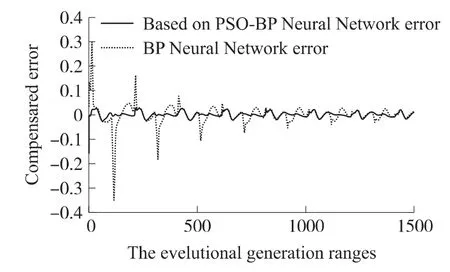
图3 训练误差曲线

由图3可以看出，基于PSO的BP神经网络的补偿精度明显比BP网络要高，PSO通过追随当前搜索的最优值进行全局寻优，成功实现避免局部极小的出现，而且补偿精度较高。

图4 工作曲线

图4 (a)为补偿前工作曲线，输出值最大相对误差为22.8%。温度补偿后在各个温度点进行仿真，如图4(b)所示。可以看出，不同温度下各工作曲线高度重合，大大消除了温度漂移，补偿后输出的最大相对误差降到了3.2%。

计算补偿后零点漂移和灵敏度漂移，与补偿前比较如表4所示。补偿后比补偿前的温度稳定性能提高了1～2个数量级，减小了温度对压力传感器输出的影响。

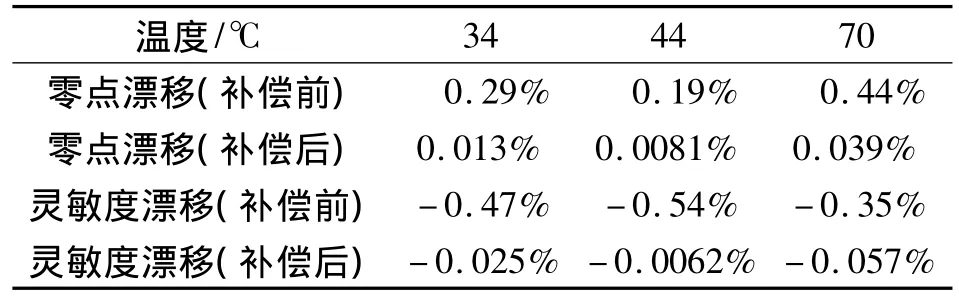
表4 补偿前后温度漂移比较

基于PSO的BP神经网络与基本的BP网络相比，收敛快，而且补偿精度较高。零点温度漂移和灵敏度温度漂移都显著减小。如表5所示，在进行补偿时，传统的BP神经网络偶尔陷入局部极小，而基于PSO的BP神经网络几乎不会陷入局部极小。

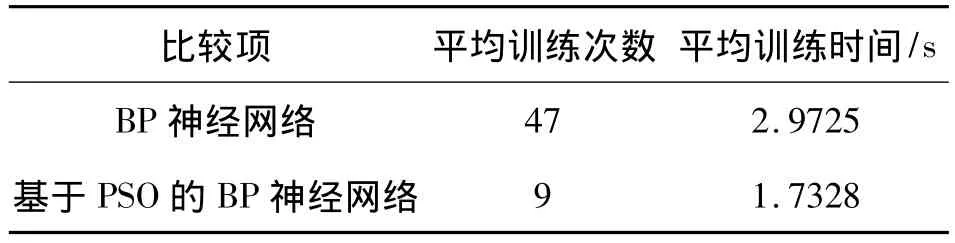
表5 BP神经网络与PSO-BP神经网络比较

4 小结

针对硅压阻式压力传感器温度漂移问题，提出了基于PSO的BP神经网络的温度补偿方法，并验证了方法的有效性，通过粒子群化算法对BP网络的极小和阈值进行全局寻优，克服了BP网络收敛速度慢和易陷入局部极小的缺陷，实验结果表明，该模型补偿精度较高，且收敛速度较快，节省运行时间，可有效避免BP神经网络收敛时陷入局部极小，其补偿效果明显优于BP网络，该方法有效的抑制了温度对压力传感器输出的影响，提高了传感器的稳定性和准确性。

［1］行鸿彦，彭基伟，吕文华，等.一种湿度传感器温度补偿的融合算法［J］.传感技术学报，2012，25(12):1711-1716.

［2］Marques M，Martin B B.Sensor Linearization with Neural Networks［J］.Industrial Electronics.2010，48(6):1288-1290.

［3］Futane N P，Roy Chowdhury S，Roy Chowdhury C，et al.ANN Based CMOS ASIC Design for Improved Temperature-Drift Compensation of Piezoresistive Micro-Machined High Resolution Pressure Sensor［J］.Microelectronics Reliability，2010，50(7):282 -291.

［4］Gao Yang，Qiu Yishen，Chen Huaixi，et al.Four-Channel Fiber Loop Ring-Down Pressure Sensor with Temperature Compensation Based on Neural Networks［J］.Microwave and Optical Technology Letters，2010，52(8):1796-1799.

［5］张朝龙，江巨浪，李彦梅，等.基于云粒子群-最小二乘支持向量机的传感器温度补偿［J］.传感技术学报，2012，25(4):472-477.

［6］Huang Y S，Young M S.An Accurate Ultrasonic Distance Measurement System with Self Temperature Compensation［J］.Instrumentation Science and Technology，2009，37(1):124-133.

［7］Futane N P，Roy Chowdhury S，Roy Chaudhury C，et al.Analog ASIC for Improved Temperature Drift Compensation of a High Sensitive Porous Silicon Pressure Sensor［J］.Analog Integrated Circuits and Signal Processing，2011，67(3):383-393.

［8］Marques M，Martin B B.Sensor Linearization with Neural Networks［J］.Industrial Electronics.2010，48(6):1288-1290.

［9］Dirk De Bruyker，Robert Puers.Thermostatic Control for Temperature Compensation of a Silicon Pressure Sensor［J］.Sensors and Actuators A:Physical，2000，82(1):120-127.

［10］Chen Chyitsong，Chang Wei-der.A Feedforward Neural Network with Function Shape Autotuning［J］.Neural Network，1996，9(4): 627-641.

［11］周晓君，阳春华，桂卫华.PSO-BP神经网络的分级过程建模［J］.计算机与应用化学，2011，28(07):825-828.

［12］Wang H S，Wang Y N，Wang Y C.Cost estimation of Plastic Injection Molding Parts through Integration of PSO and BP Neural Network［J］.Expert Systems with Applications，2013，40(08):418 -428.

孙艳梅(1979-)，女，吉林前郭人，讲师，硕士，主要研究方向为传感器技术，sym791122@163.com。

基于PSO的BP神经网络在压力传感器温度补偿中的应用*

孙艳梅*，苗凤娟，陶佰睿
(齐齐哈尔大学通信与电子工程学院，黑龙江齐齐哈尔161006)

针对硅压阻式压力传感器的温度漂移问题，提出了基于粒子群优化算法PSO(Particle Swarm Optimization Algorithm)的BP神经网络的温度补偿模型，通过粒子群化算法对BP网络的权值和阈值进行全局寻优，克服了BP网络收敛速度慢和易陷入局部极值的缺陷，而且温度补偿的精度较高。研究结果表明，该方法有效的抑制了温度对压力传感器输出的影响，提高了传感器的稳定性和准确性。

温度补偿;粒子群优化算法;BP神经网络;压力传感器

TP212

A

1004－1699(2014)03－0342－05

2013-12-23修改日期:2014-03-09

C:2520C;2560L

10.3969/j.issn.1004－1699.2014.03.013

项目来源:国家自然科学基金项目(61204127);黑龙江省自然科学基金项目(F201332);黑龙江省普通高等学校新世纪优秀人才培养计划项目(1253-NECT025)