基于分层壳单元与纤维梁单元组合剪力墙滞回性能分析

王文达，杨全全，李华伟

(兰州理工大学 甘肃省土木工程防灾减灾重点实验室，兰州 730050)

现代建筑向超高层、复杂功能发展，钢、混结构应用广泛。传统混合结构如外钢框架-钢筋混凝土核心筒体系钢筋混凝土剪力墙或筒体作为主要抗侧力构件，地震发生时因其延性差，随裂缝不断开展，混凝土剪力墙会逐渐退出，外围框架需承担更多水平荷载，整个体系因此遭破坏。考虑钢筋混凝土剪力墙构件受力特点，可通过将钢筋混凝土剪力墙设计成带边框柱的钢-混凝土组合剪力墙提高其延性[1]。带边框柱钢-混凝土组合剪力墙体系中，墙板一般用钢筋混凝土结构，边框柱采用钢管混凝土或型钢混凝土等组合柱形式，以提高对剪力墙的约束效果，增强整体结构的抗震性能。曹万林等[2]对3榀钢管混凝土边框柱剪力墙进行低周往复荷载的抗震性能试验表明其抗震性能良好；王敏等[3]经对2榀钢管混凝土边框柱剪力墙进行低周反复荷载试验研究表明，高轴压比组合剪力墙抗震性能更好；Liao等[4]对4榀圆钢管混凝土边框柱剪力墙进行低周往复荷载试验结果表明，轴压比、高宽比对组合剪力墙延性及耗能能力影响较大；Fumiya等[5]对4榀型钢混凝土边框柱剪力墙体系进行往复加载试验，研究加载速度与型钢布置对剪力墙力学性能影响；梁兴文等[6]通过对8榀采用高强混凝土型钢混凝土边框柱剪力墙进行拟静力试验结果表明，该类剪力墙在适当轴压比及配钢率下变形能力较强；Liao等[7]对3榀型钢混凝土边框柱剪力墙体系进行低周往复荷载试验及参数分析；钱稼茹等[8]对5榀型钢混凝土边框柱剪力墙进行往复水平加载试验结果表明，墙端约束边缘构件对提高高轴压比剪力墙变形能力作用显著；Wallace等[9]对2榀钢管混凝土边框柱剪力墙与4榀型钢混凝土边框柱剪力墙进行水平荷载作用试验，研究不同轴压比对剪力墙抗震性能影响。

以上试验研究表明，采用组合柱为边框柱形成的组合剪力墙体系因边框柱约束效果，组合剪力墙抗震性能良好；但对组合剪力墙结构体系数值模拟研究较少。Liao等[7]基于有限元软件ABAQUS采用三维实体单元对3榀型钢混凝土边框柱剪力墙与3榀钢筋混凝土暗柱剪力墙进行模拟，与试验结果吻合良好；王文达等[10]基于Opensees平台对6榀钢管混凝土边框柱剪力墙进行低周往复加载试验数值模拟，取得良好效果；夏汉强等[11]用SAP2000软件对矩形钢管混凝土边框柱剪力墙进行分析，结果符合相关技术规程结构分析假定。

本文基于对有限元软件ABAQUS二次开发技术，分别采用纤维梁单元、分层壳单元建立组合剪力墙体系数值模型，对钢管混凝土边框柱-RC剪力墙及型钢混凝土边框柱-RC剪力墙两类钢与混凝土组合剪力墙体系的滞回试验结果进行数值模拟，并对比了组合剪力墙体系数值模拟破坏特征，与试验结果总体吻合良好。本文方法可为实现高层建筑钢与混凝土混合结构体系抗震性能有效、准确的数值模拟分析提供参考。

1 纤维梁单元在组合剪力墙模型中应用

ABAQUS中有6种常用梁单元，包括铁木辛柯梁单元(B21，B31，B22，B32)及Euler-Bernoulli梁单元(B23，B33)，其中B31，B32，B33均为空间梁单元。本文用B31梁单元模拟组合剪力墙边框柱时，将钢材离散成若干纤维，在程序中通过*rebar关键字定义钢纤维，以此模拟组合边框柱中钢管、型钢或钢筋。如模拟钢管混凝土边框柱时，采用16根钢纤维模拟钢管，见图1(实心圆点)，通过调整混凝土本构关系近似体现钢管对核心混凝土的约束作用[12]。

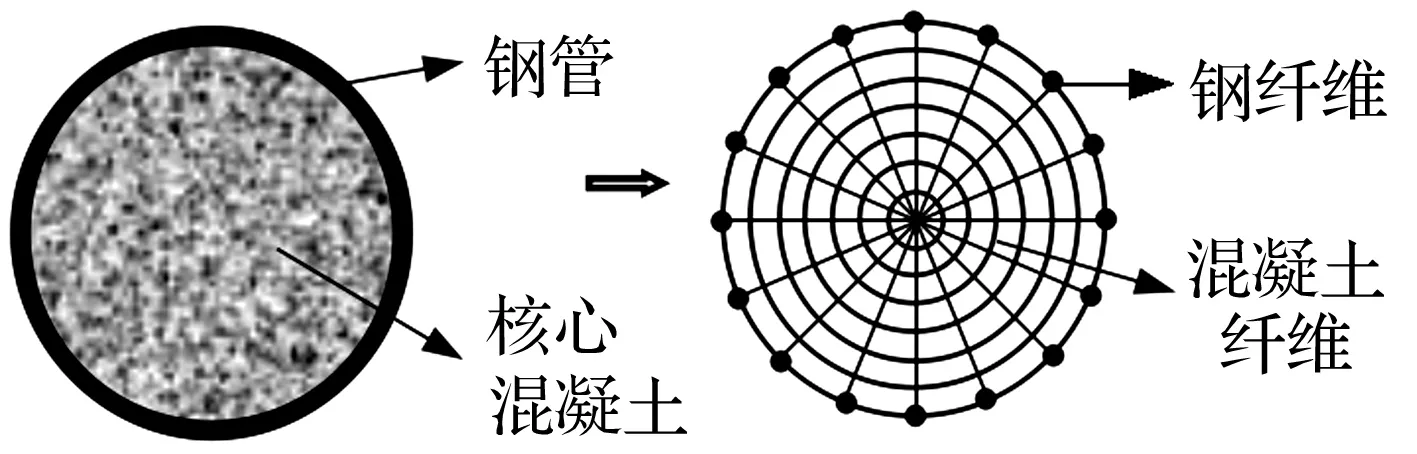
图1 钢管混凝土柱截面纤维划分

2 分层壳单元在组合剪力墙模型中应用

分层壳模型为将一个壳单元划分成若干层，见图2，再据剪力墙实际情况设置每层厚度及材料性质(混凝土或钢筋)。用有限元计算时先获得壳单元中心层应变及曲率，据各层材料间满足平截面假定，可由中心层应变、曲率获得各混凝土层及钢筋层应变，再由各自材料本构方程获得相应应力。采用积分获得整个壳单元内力[13]。分层壳单元优点为考虑剪力墙面内弯矩-面内剪切-面外弯曲间耦合，可更准确模拟实际工程剪力墙复杂的非线性力学行为。

在ABAQUS中对剪力墙结构模拟中，二维问题采用平面应力单元，三维问题采用壳单元[12]。选取材料本构模型时混凝土可选ABAQUS自带塑性损伤模型(Concrete Damaged Plasticity)或弥散裂缝模型(Concrete Smeared Cracking)，钢筋可用软件自带的弹塑性本构关系。

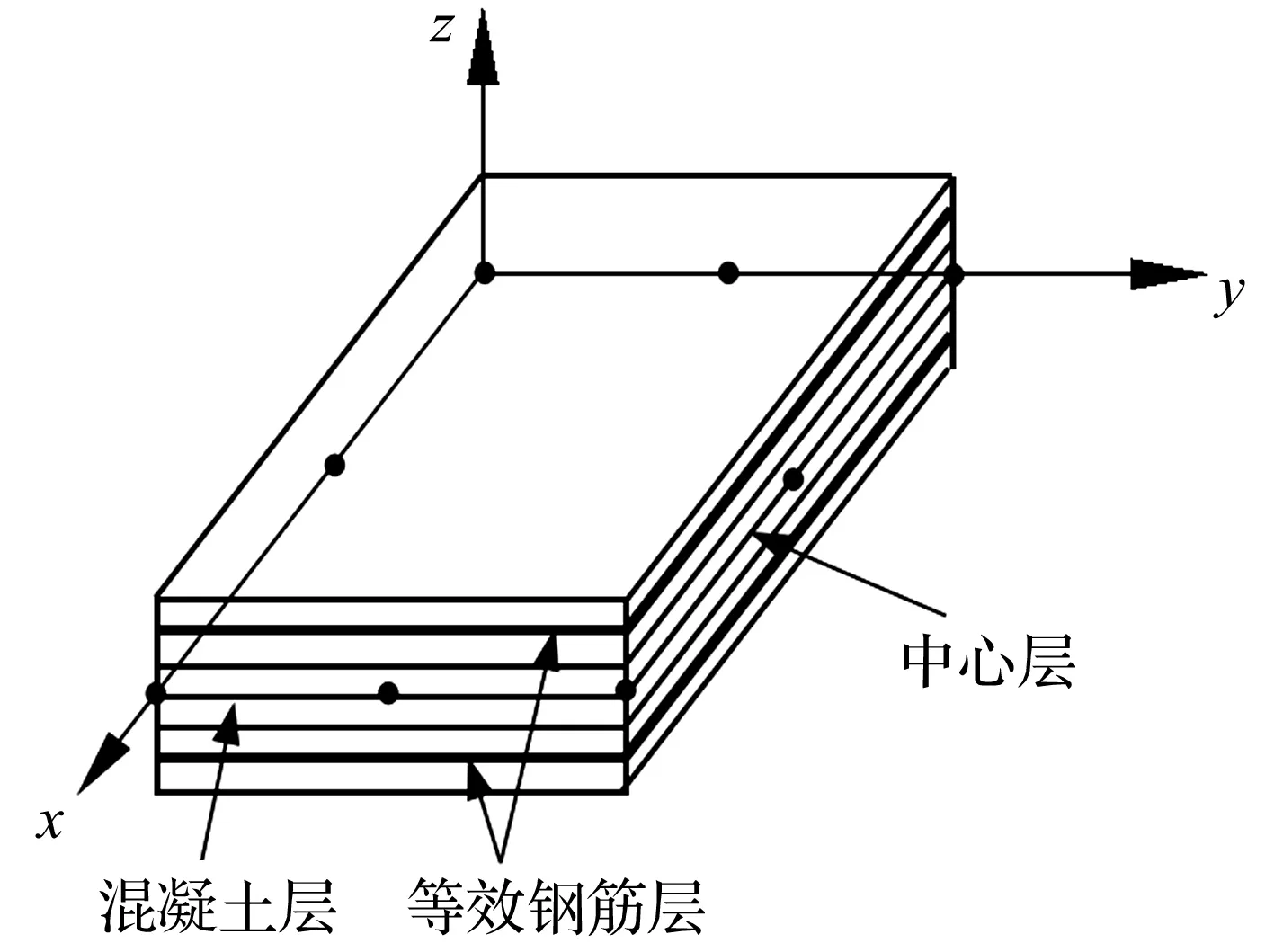
图2 分层壳单元模型

剪力墙有限元模型创建关键在于钢筋合理模拟，ABAQUS中有两种方式可实现钢筋模拟，即分离式、组合式。分离式即将剪力墙中每根钢筋单独建模，再通过软件中节点耦合或嵌入(Embed)等功能使钢筋网片与墙体共同工作；组合式即将钢筋弥散于墙体内，适用于钢筋分布均匀区域。对墙端配筋较密的钢筋则采用分离式较方便。本文因端柱由梁单元模拟，墙体均匀配筋，故采用组合式创建钢筋网片。

3 数值模型建立

3.1 建模方法

在ABAQUS中用B31梁单元创建边框柱部件，并赋予混凝土材性，再通过*rebar关键字将钢纤维添入，给出每根纤维材料属性、截面名称、截面面积及截面相对坐标。用S4壳单元创建墙板部件，在“Rebar Layers”中定义各层钢筋属性。通过共节点绑定方式将边框柱梁单元与墙板壳单元连接，使二者能协同作用抵抗水平荷载。

3.2 材料本构模型

3.2.1 剪力墙混凝土本构模型

剪力墙混凝土采用ABAQUS中塑性损伤模型，其中受压性能采用文献[14]附录C中单轴受压应力-应变关系，考虑ABAQUS用能量准则定义混凝土受拉软化性能时计算收敛性较好，故采用开裂应力-断裂能关系考虑受拉性能。在混凝土受压性能中定义损伤因子，用应力应变关系通过Sidiroff能量等价原理推导的公式[15]为

(1)

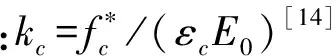
3.2.2 钢管混凝土柱中核心混凝土本构模型

钢管混凝土边框柱中核心混凝土受压骨架曲线采用考虑钢管约束效应的单轴应力-应变关系[1]。受压加卸载准则采用加载、再卸载原则[16]，见图3，在受压段卸载至残余应变后，应力值保持为0，直至进入受拉段。再加载时按原卸载路径进行，直至回到受压骨架线。受压卸载的残余应变εz的计算式为

(2)

式中：Ec0为混凝土初始弹性模量；εc0为峰值应力对应的应变；σcun,i，εcun,i分别为第i次卸载处应力、应变；εca为计算过渡量。

混凝土受拉骨架线采用双折线模型，受拉开裂应力计算式[17]为

(3)

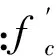
在受拉侧卸载时指向原点，再加载时按卸载路径回到受拉骨架曲线。

3.2.3 型钢混凝土柱中混凝土本构模型

型钢混凝土边柱中混凝土采用修正Kent-Park模型[18]，该模型能考虑型钢混凝土柱中箍筋对混凝土的约束效应。受压骨架线及加卸载准则见图4，具体表达式为

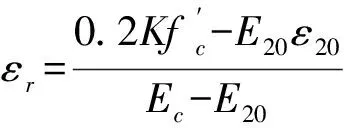
(4)

式中：σr，εr分别为虚拟点R处应力、应变；ε0为对应于应力峰值点A处应变；ε20为对应于0.2倍应力峰值点B处应变；fc为混凝土圆柱体抗压强度；Ec为骨架线上升段初始弹性模量；K为箍筋约束效应系数；σm,i，εm,i分别为第i次卸载处应力、应变；Er,i为第i次卸载刚度。

受拉骨架线为带软化段的双线型，且在受拉侧卸载时指向原点或上次残余应变点。

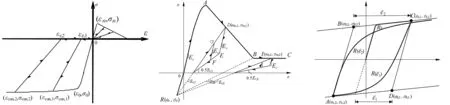
图3 核心混凝土单轴本构模型

3.2.4 钢材本构模型

钢管、型钢及钢筋采用考虑包辛格效应的Menegotto-Pinto修正模型[19]，见图5。具体表达式为

(5)

式中：σ0，ε0分别为两条渐近线交点(B或D)处应力、应变；σr，εr分别为应变逆转点(A或C)处应力、应变；R为曲线过渡参数，计算时建议R0=20，R1=18.5，R2=0.15；εy，εm为屈服应变、历史最大应变。

基于以上材料本构模型，利用ABAQUS软件用户材料子程序接口UMAT将混凝土、钢材本构模型编制材料单轴滞回本构模型子程序。本文在用纤维梁单元模拟循环荷载作用组合边框柱时调用该子程序。

4 算例验证

4.1 钢管混凝土柱-钢梁平面框架模拟

为验证非线性纤维梁单元建模方法及材料本构模型的合理性，选钢管混凝土平面框架进行数值模拟，对3榀单层单跨钢管混凝土柱-钢梁平面框架在水平往复荷载作用下试验结果[20]进行模拟，试件具体参数见文献[19]，计算所得荷载(P)-位移(Δ)滞回曲线与试验曲线对比见图6。由图6看出，计算滞回曲线的刚度退化及捏缩效应均与试验结果吻合较好，但计算所得承载力略低于试验结果，主要因采用梁单元模拟框架时不能采取加强构造措施(如柱脚加劲板)，且在通过添加钢纤维方式模拟钢管时不能考虑与钢梁节点刚域。总体上，采用纤维梁单元模拟钢管混凝土框架滞回性能效果较好。

4.2 钢筋混凝土暗柱剪力墙单调加载试验模拟

为验证建模方法的正确性，对3榀[21]及2榀[22]带钢筋混凝土暗柱剪力墙进行单向推覆试验的数值模拟，几何、材料参数见表1。经与试验对比知，二者结果吻合较好，单调加载骨架曲线与试验曲线对比见图7，采用分层壳单元模拟钢筋混凝土剪力墙能取得良好效果。

图6 钢管混凝土框架计算与试验荷载(P)-位移(Δ)滞回曲线对比

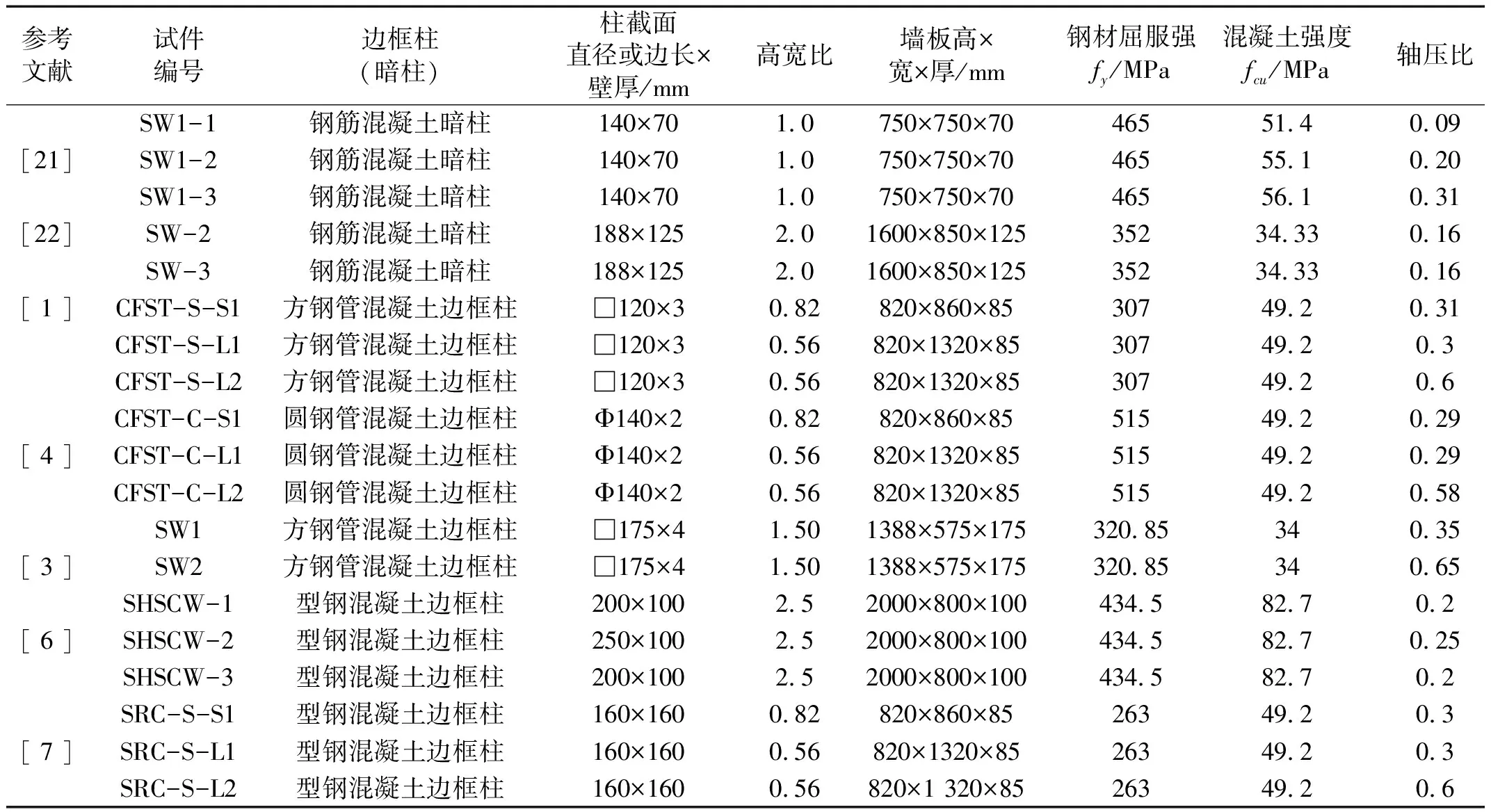
表1 试件几何参数与材料参数

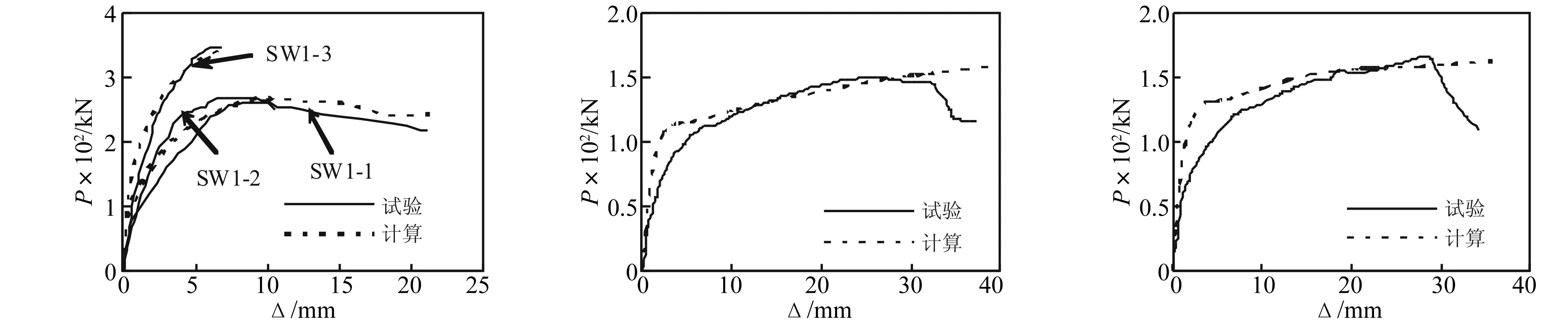
(a) SW1-1～SW1-3[21] (b) SW-2[22] (c) SW-3[22]

4.3 钢管混凝土边框柱剪力墙滞回曲线计算

用所述建模方法对8榀带钢管混凝土边框柱的组合剪力墙[1,3-4]进行低周往复加载试验的数值模拟。试件参数见表1。计算所得荷载(P)-位移(Δ)滞回曲线与试验曲线对比及单调加载曲线见图8。由图8看出，计算结果在抗剪承载力、捏缩效应、刚度退化及延性方面均与试验结果基本吻合，但计算初始刚度偏大于试验，原因为计算分析中模型底部选完全固结约束(即刚接)而试验中并非理想的完全固结，故分析中对结果有一定影响。

图8 钢管混凝土边框柱剪力墙计算与试验荷载(P)-位移(Δ)滞回曲线对比

4.4 型钢混凝土边框柱剪力墙滞回曲线计算

用所述建模方法对6榀带型钢混凝土边框柱的剪力墙[6-7]进行低周往复加载试验的数值模拟。各剪力墙几何尺寸及部分材料参数见表1。计算所得荷载(P)-位移(Δ)滞回曲线与试验曲线对比及单调加载曲线见图9。由图9看出，滞回曲线在抗剪承载力、捏缩效应、刚度退化及延性方面均与试验结果较吻合。

由以上模型验证得知，基于ABAQUS软件、采用分层壳单元及纤维梁单元模拟组合柱-钢筋混凝土组合剪力墙体系方法及本文的本构模型子程序能较好模拟带组合边框柱剪力墙抗剪承载力、捏缩效应、刚度退化及延性等性能，且可提高计算效率。

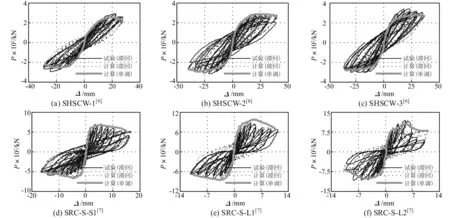
图9 型钢混凝土边框柱剪力墙计算与试验荷载(P)-位移(Δ)滞回曲线对比

5 组合剪力墙破坏形态对比分析

以剪力墙试件CFST-S-L1[1](高宽比0.56)、SHSCW-2[6](高宽比2.5)为例分别对钢管混凝土边框柱剪力墙、型钢混凝土边框柱剪力墙计算获得破坏形态与试验实测图片进行对比分析。

5.1 钢管混凝土边框柱剪力墙破坏形态分析

ABAQUS软件中采用塑性损伤模型的混凝土出现主拉塑性应变时表示该混凝土已开裂，因此本文将墙板主拉塑性应变矢量图与试验实测裂缝模态对比知基本能反映墙板混凝土开裂状况；墙板主拉塑性应变云图中应变较大区域表示裂缝宽度较大，本文给出的墙板主拉塑性应变云图可用于反映墙板混凝土裂缝宽度大小。以钢管混凝土边框柱剪力墙CFST-S-L1[1]为典型试件，选3典型时刻对应特征点进行分析，3个特征点分别选墙板出现初始裂缝、组合剪力墙达峰值荷载时、荷载下降到85%极限荷载时(最终破坏时刻)。对每个特征点分别给出主拉塑性应变矢量图、主拉塑性应变云图及实测裂缝模态。

(1) 墙板出现初始裂缝时刻。试验过程中水平荷载P=594 kN时墙板出现第一条剪切斜裂缝，裂缝宽度达0.18 mm，与水平方向夹角约37。[1]；计算分析P=494.3 kN时，墙板右下方混凝土单元达到抗拉强度开裂，墙板出现初始裂缝时混凝土裂缝分布见图10。由图10看出，裂缝方向(垂直于箭头方向)约45°，与试验结果较接近。

(2) 组合剪力墙达峰值荷载时刻。试验过程中水平荷载达P=967.9 kN时试件达峰值荷载，计算模拟峰值荷载为989.5 kN。组合剪力墙达到峰值荷载时墙板混凝土裂缝分布见图11。由图11看出，峰值荷载时刻裂缝贯穿整个墙体，沿45°方向开展，且在墙体中部裂缝宽度较大，接近实测结果。

图10 墙板初始裂缝图

图11 峰值荷载时刻裂缝分布图

图12 最终破坏时刻裂缝分布图

(3) 85%极限荷载时刻。试件最终破坏时墙板由斜裂缝分割形成混凝土斜压小柱体达到抗压强度碎裂。最终破坏时刻墙板混凝土裂缝分布见图12。由图12看出，墙体左下部破坏较严重，裂缝宽度较大，与实测结果较接近。

5.2 型钢混凝土边框柱剪力墙破坏形态分析

SHSCW-2[6]为高宽比较大的型钢混凝土边框柱剪力墙。在水平荷载作用下最终在平面内发生弯曲破坏，见图13(a)。水平荷载P=131.4 kN时，墙板右下侧出现裂缝，底部出现水平弯曲裂缝，见图13(b)。随荷载增大，开裂范围逐渐扩大，出现交叉斜裂缝，剪力墙底部形成变形集中的塑性铰区域。P=282.2 kN时，剪力墙达峰值荷载，裂缝分布见图13(c)。水平荷载下降到85%峰值荷载时，因底部混凝土达抗压强度碎裂，试件破坏。最终破坏形态及裂缝分布见图13(d)～(f)。由图13(d)～(f)看出，剪力墙底部破坏严重，与实测结果破坏情况一致。

图13 型钢混凝土边框柱剪力墙破坏形态

6 结 论

通过对带组合边框柱的剪力墙结构低周往复试验数值模拟与滞回性能分析，结论如下：

(1) 基于ABAQUS软件，采用纤维梁单元、分层壳单元能较准确、有效模拟带钢筋混凝土暗柱、钢管混凝土及型钢混凝土组合边框柱剪力墙的滞回性能。通过滞回曲线对比，其抗剪承载力、刚度退化及捏缩效应均与试验结果较吻合。

(2) 利用ABAQUS软件后处理功能，输出的剪力墙墙板最大主塑性应变矢量图及云图能较准确描述剪力墙裂缝发展及破坏形态，可为实现超高层建筑钢与混凝土混合结构体系抗震性能有效、准确的数值模拟分析提供参考。

[1] 韩林海,陶忠,王文达. 现代组合结构和混合结构-试验、理论和方法[M]. 北京:科学出版社,2009.

[2] 曹万林,王敏,张建伟,等.钢管混凝土边框剪力墙抗震试验及承载力计算[J].北京工业大学学报,2008,34(12):1291-1297．

CAO Wan-lin, WANG Min,ZHANG Jian-wei, et al. Seismic experiment and load-carring capacity calculation of shear wall with concrete filled steel tube columns[J]. Journal of Beijing University of Technology, 2008, 34(12):1291-1297.

[3] 王敏,曹万林,张建伟,等.不同轴压比下钢管混凝土边框组合剪力墙抗震性能研究[J].世界地震工程,2008,24(2):32- 36．

WANG Min, CAO Wan-lin, ZHANG Jian-wei, et al. Seismic behavior research of composite shear wall with concrete filled steel tube columns for different axial-load ratios[J]. World Earthquake Engineering, 2008, 24(2): 32-36.

[4] Liao Fei-yu, Han Lin-hai, Tao Zhong. Seismic behaviour of circular CFST columns and RC shear wall mixed structures: experiments[J]. Journal of Constructional Steel Research, 2009, 65(8/9):1582-1596.

[5] Fumiya E, Masayuki O. Effect of loading velocity on mechanical behavior of SRC shear walls[J]. Univ Southern California, School Engn, Dept Civil Engnlos Angeles, 2000, 1/2:809-816.

[6] 梁兴文,马恺泽,李菲菲,等．型钢高强混凝土剪力墙抗震性能试验研究[J]．建筑结构学报,2011,32(6):68-75.

LIANG Xing-wen,MA Kai-ze, LI Fei-fei, et al. Experimental study on seismic behavior of SHSC structural walls[J]. Journal of Building Structures, 2011, 32(6): 68-75.

[7] Liao Fei-yu, Han Lin-hai, Tao Zhong. Performance of reinforced concrete shear walls with steel reinforced concrete boundary columns[J]. Engineering Structures,2012,44:186-209.

[8] 钱稼茹,魏勇,赵作周,等．高轴压比钢骨混凝土剪力墙抗震性能试验研究[J]．建筑结构学报,2008,29(2):43-50．

QIAN Jia-ru,WEI Yong,ZHAO Zuo-zhou,et al. Experimental study on seismic behavior of SRC shear walls with high axial force ratio[J]. Journal of Building Structures, 2008, 29(2): 43-50.

[9] John W,Rakcal K, Chelan M, et al. Lateral-load behavior of shear walls with structureal steel boundary columns[J]. Univ Southern California, School Engn, Dept Civil Engnlos Angeles,2000,1/2: 801-808.

[10] 王文达,魏国强,李华伟．钢管混凝土框架-RC剪力墙混合结构滞回性能分析[J]．振动与冲击,2013,32(15):41-46．

WANG Wen-da, WEI Guo-qiang, LI Hua-wei. Hysteresis behavior analysis of the mixed structures with concrete-filled steel tubular frame and RC shear wall[J]. Journal of Vibration and Shock, 2013, 32(15): 41-46.

[11] 夏汉强,刘嘉祥．矩形钢管混凝土柱带框剪力墙的应用及受力分析[J]．建筑结构,2005,35(1):16-18．

XIA Han-qiang, LIU Jia-xiang. Application and structural analysis of shear wall connected with rectangular concrete-filled steel tube columns[J]. Building Structure, 2005, 35(1): 16-18.

[12] 陆新征,叶列平,缪志伟,等．建筑抗震弹塑性分析-原理、模型与在ABABQUS, MSC.MARC和SAP2000上的实践[M]．北京：中国建筑工业出版社,2009．

[13] 叶列平,陆新征,马千里,等．混凝土结构抗震非线性分析模型、方法及算例[J]．工程力学,2006,23(S2):131-140．

YE Lie-ping, LU Xin-zheng, MA Qian-li,et al. Nonlinear analytical models, methods and examples for concrete structures subject to earthquake loading[J]. Engineering Mechanics, 2006, 23(S2):131-140.

[14] GB50010-2010,混凝土结构设计规范[S].

[15] 曹明．ABAQUS损伤塑性模型损伤因子计算方法研究[J]．交通标准化,2012,40(2):51-54．

CAO Ming.Research on damage plastic calculation method of ABAQUS concrete damaged plasticity model[J]. Communications Standardization, 2012, 40 (2): 51-54.

[16] Mander J B, Priestley M J N, Park R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering,ASCE, 1988, 114(8):1804-1826.

[17] 沈聚敏,王传志,江见鲸．钢筋混凝土有限元与板壳极限分析[M]．北京：清华大学出版社,1990．

[18] Kent D C, Park R. Flexural members with confined concrete[J]. Journal of the Structural Division, ASCE, 1971, 97(7): 1969-1990.

[19] Menegotto M, Pinto P E. Method of analysis for cyclically loaded R.C. plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[C]//.Proceeding, Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads. International Association for Bridge and Structural Engineering, Zurich, Switzerland, 1973:15-22.

[20] 王文达,韩林海,陶忠．钢管混凝土柱-钢梁平面框架抗震性能的试验研究[J]．建筑结构学报,2006,27(3):48-58．

WANG Wen-da, HAN Lin-hai, TAO Zhong. Experimental research on seismic behavior of concrete filled CHS and SHS columns and steel beam planar frames[J]. Journal of Building Structures, 2006, 27(3): 48-58.

[21] 郑万仁．不同轴压比下混凝土剪力墙结构性能研究[D]．上海：同济大学，2004．

[22] 章红梅,吕西林,鲁亮,等．边缘约束构件对钢筋混凝土剪力墙抗震性能的影响[J]．地震工程与工程振动，2007，27(1)：92-98．

ZHANG Hong-mei, LÜ Xi-lin, LU Liang, et al. Influence of boundary element on seismic behavior of reinforced concrete shear walls[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(1): 92-98.