移动荷载作用下路面动力响应试验研究

陈恩利，刘永强，赵进宝

(1.石家庄铁道大学 机械工程学院，石家庄 050043；2.河北省交通安全与控制重点实验室，石家庄 050043)

由于公路交通量增加、行车速度提高、车辆轴重加大，致公路早期破坏严重[1-5]，路面结构在移动荷载作用下的动力学行为已成关注重点。对路面动力学研究主要有理论研究及现场试验两种。理论研究主要对简化的力学模型进行分析，且已取得较多理论与数值仿真成果[6-14]。试验研究主要通过现场测试对所得路面结构内部应力、应变、湿度及温度等参数进行分析[15-17]。此类问题目前存在困难：①由于现场试验与理论模型相差甚远，试验结果难以与理论结果对比验证；②进行实际路面结构动力学试验需耗费巨大财力、物力，成本高试验困难；而模型试验可在实验室进行[18]，便于控制试验条件进行规律性研究，试验精度较高。模型试验可为理论计算结果提供验证，亦可为现场试验提供前期研究基础与数据支持；因此，开展车路系统路面结构模型动力学试验研究，对深入了解路面结构在移动荷载作用下的动态响应具有重要经济与实际意义。

本文设计制作的移动简谐激励装置、单自由度1/4车辆模型及分布刚度路面模型，利用试验与数值仿真方法研究移动简谐激励及1/4汽车模型作用下分布刚度路面动力响应，并通过试验方法研究冲击荷载作用下路面动力响应，对深入了解路面结构在移动荷载作用下动态响应具有一定参考。

1 试验系统设计

1.1 车辆模型一

模型一可为路面提供简谐激励。该模型由四轮小车、调速电机及质量块组成，见图1。调速电机输出轴端连接质量块，电机带动质量块旋转产生离心力，该力竖向分量即向路面提供的简谐激励。通过调节电机转速，可实现不同激励频率。

图1 谐振源车辆模型

1.2 车辆模型二

模型二为1/4车辆模型，由质量块、弹簧、阻尼器、车轮、支承板及导杆组成，见图2。导杆上端固定于支承架，其作用使质量块在竖直方向自由滑动。在质量块及支承板上均装有直线轴承，以减小导杆及质量块与支承板摩擦。

图2 1/4车辆模型

1.3 路面-路基模型

该模型设计成分布刚度形式，主要由钢制梁路面与弹簧支承结构(刚度K)组成，见图3。弹簧上端与路面连接，下端固定于弹簧固定板，弹簧固定板置于带导向槽地面，路面高度通过路面两端支架调节。

图3 分布刚度路面-路基模型

1.4 路面冲击激励模型

为研究路面冲击载荷的动力响应，设计冲击路面实验模型。距路面一端1/4处设置高度3 mm半圆柱障碍模拟车辆对路面的冲击激励，见图4。

图4 路面冲击激励模型

1.5 试验设备及试验过程

试验主要设备有INV306U智能信号采集处理分析仪及振动信号分析系统、WY-30应变式位移计、MCC-8A数字动态采集仪、光电开关、数字计数显示器、电器柜及动力装置。试验装置总体布置见图5，动力装置通过钢丝绳牵引车辆模型从路面一端匀速驶向另一端。

图5 试验装置总体布置

通过模态实验、自由衰减振动、抗弯刚度测试等测定系统模态频率、振型、阻尼等参数，为数值仿真计算提供依据。在此基础上，研究不同速度、不同简谐激励频率作用下的路面动力响应；分别研究光滑路面及考虑冲击激励路面两种情况下1/4车辆模型对路面的动力响应。

2 动力学分析及数值仿真

2.1 弹性支撑路面在简谐激励作用下振动 响应分析

用两端简支有限长伯努利欧拉梁模拟路面，用温克尔弹性地基模拟路基，并设t=0时汽车位于简支梁路面左端匀速行驶，行驶中始终与路面接触。建立移动简谐激励作用的温克尔地基梁路面力学模型见图6。

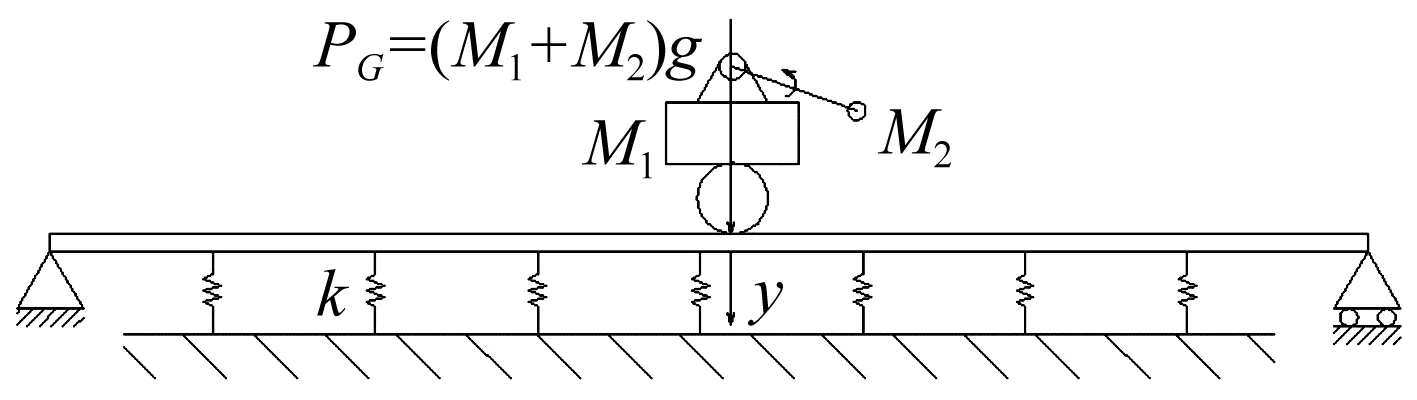
图6 移动简谐力作用下温克尔地基梁模型

受移动简谐激励作用的温克尔地基梁路面垂向振动微分方程为

ky(x，t)=δ(x-Vt)P(x，t)

(1)

P(x，t)=δ(x-Vt)[(M1+M2)g-

(2)

其中：k为温克尔地基弹性系数；EI为简支梁路面抗弯刚度；m为简支梁路面单位长度质量；P(x,t)为路面外荷载，包括移动荷载重力、惯性力及简谐激励力。

按阵型分解法求解式(1)，设简支梁路面垂向位移为

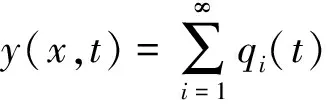
(3)

将式(3)代入式(1)、(2)整理得：

(4)

由式(4)可得在移动简谐激励作用下汽车-路面耦合系统运动方程前N阶矩阵表达式：

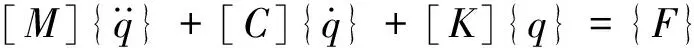
(5)

式(5)为时变系数的二阶微分方程组，可采用逐步积分Newmark-β法进行数值求解。

2.2 弹性支承路面在1/4汽车模型作用下振动分析

将汽车系统简化为单自由度1/4汽车模型，研究该模型作用的弹性支承路面动力响应。用有限长伯努利欧拉梁模拟路面，设路面两端简支，用温克尔地基模拟路基。设汽车模型行驶中车轮始终与路面接触，t=0时汽车位于梁左端，且匀速通过简支梁，建立二维汽车-路面系统力学模型见图7。

图7 二维汽车-路面系统力学模型

图7的车路系统运动微分方程为

(6)

ky(x，t)=δ(x-Vt)[(M1+M2)g-

(7)

式中：Z(t)为车体在t时刻竖向位移；k，k1为地基弹性系数、汽车悬架刚度；c，c1为简支梁、汽车悬架阻尼系数；EI为简支梁抗弯刚度；m为简支梁单位长度质量。

同理，用振型分解法可得解耦的离散微分方程为

(8)

整理式(8)得：

(9)

(10)

车路系统前N+1阶矩阵表达式为

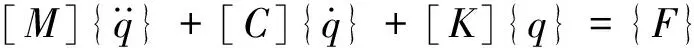
(11)

3 试验结果分析

3.1 移动简谐激励作用下路面动力响应

在谐振频率f=2.2 Hz作用下，车辆模型分别以0.1 m/s、0.2 m/s、0.3 m/s及0.4 m/s速度驶过路面时，路面中点处垂向位移变化曲线见图8～图11。由四图看出，试验值与数值解基本重合，说明刚性路面可用均布弹簧支承代替连续支承进行试验，试验数据能反映实际工程中路面结构的振动问题。试验值、数值解均呈正弦变化。随速度的增加，路面动力效应明显，但动力作用影响时间缩短，位移曲线幅值增大，频率降低。

3.2 弹性支承路面在1/4车辆模型作用下的试验分析

1/4车辆模型分别以0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s速度驶过路面时测量路面中点处垂向位移变化情况；用数值仿真方法计算连续支承条件下路面中点挠度变化值。数值解与试验结果对比见图12～图15。由四图看出，两条曲线基本重合，说明用钢梁模拟路面时选足够多分布支承，可代替连续支承研究车路系统中车辆与路面相互作用。路面垂向位移试验值曲线出现不光滑现象，此因模型小车行驶过程中支承架上尼龙轮与导轨间摩擦所致。

图8 f=2.26 Hz, v=0.1 m/s时路面位移

图11 f=2.26 Hz, v=0.4 m/s时路面位移

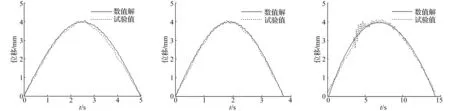
图14 v=0.3 m/s时路面中点处位移

3.3 冲击作用下车路耦合试验

1/4车辆模型无阻尼器时以0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s速度驶过有冲击效应路面时，路面中点处垂向位移变化曲线与数值解对比见图16～图19。由四图看出，因路面不平度引起的车辆振动反作用于路面产生动力响应，作用效果明显。随速度的增加，由车辆振动引起的路面位移曲线幅值先增加后减小，且衰减快。

1/4车辆模型有阻尼器时分别以0.1 m/s、0.2 m/s、0.3 m/s、0.4 m/s速度驶过有冲击激励路面时，路面中点处垂向位移变化曲线与数值解对比见图20～图23。由四图看出，由于阻尼器的作用，车辆振动急剧衰减，引起路面响应较小。随速度的增加，由车辆振动引起的路面位移曲线幅值逐渐增大。

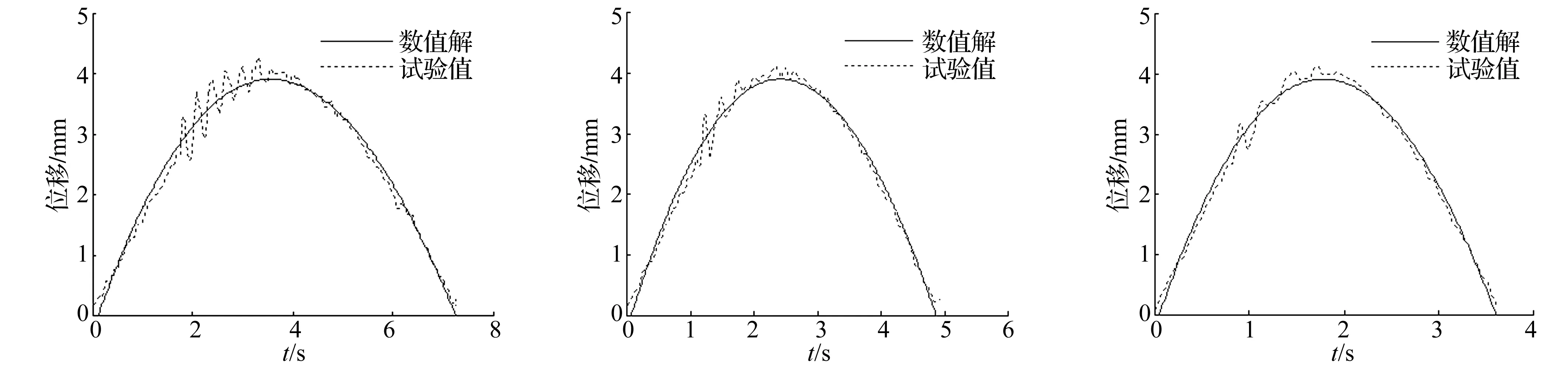
图17 无阻尼v=0.2 m/s时路面中点位移

图20 有阻尼v=0.1 m/s时路面中点位移

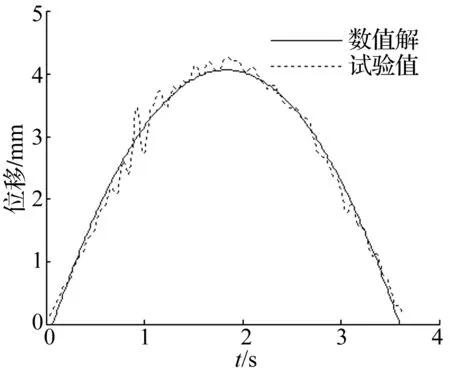
图23 有阻尼v=0.4 m/s时路面中点位移

4 结 论

本文通过设计制作车路试验模型系统，并利用试验、数值仿真方法相互验证移动简谐激励与1/4汽车模型作用下分布刚度路面动力响应的正确性，研究冲击荷载作用下1/4车辆对路面动力响应。结论如下：

(1) 移动简谐激励作用下路面垂向位移曲线类似以一定频率振动的正弦波。随速度的增加，位移曲线波动幅值增大，频率降低，周期变长。

(2) 刚性路面可用均布弹簧支承代替连续支承进行试验，且结果较满意；利用模型实验研究路面动力响应可行。

(3) 本文所建实验系统结构合理，实验效果明显，可近似满足刚性路面动力学响应测试需要。

[1] 朱孔源,余群.车辆-路面相互作用系统的研究现状和展望[J].西安公路交通大学学报,2001, 21(2): 6-10.

ZHU Kong-yuan, YU Qun. Study reality and prospect on the interaction of vehicle and pavement[J].Journal of Xi’an Highway University, 2001, 21(2):6-10.

[2] 陆辉,孙立军,李套岭. 国内路面动力学研究概述[J]. 上海公路, 2002(6):6-9.

LU Hui, SUN Li-jun, LI Tao-ling. Research overview of domain road dynamics study[J]. Shanghai Highways, 2002(6):6-9.

[3] Yang S P, Li S H, Lu Y J. Dynamics of Vehicle-pavement coupled system based on a revised flexible roller contact tire model[J]. Science in China, Series E: Technological Sciences, 2009, 52 (3): 721-730.

[4] 高华. 基于车路系统分析的路面动力学研究方法[J]. 交通科技, 2007(2): 84-86.

GAO Hua. The road dynamics of systems analysis methods based on the vehicle-road system[J]. Transportation Science & Technology, 2007(2): 84-86.

[5] 吕彭民, 董忠红. 车辆-沥青路面系统动力学分析[M]. 北京: 人民交通出版社, 2010.

[6] Fryba L. Infinite beam on an elastic foundation subjected to a moving load[J]. Aplikace Matematiky, 1957, 12(2):105-132.

[7] Kenny J T. Steady-state vibrations of beam on elastic foundation for moving load[J]. Journal of Applied Mechanics, 1954, 21(4):359-364.

[8] Steele C R.The finite beam on a moving load[J]. Journal of Applied Mechanics,1967,35(4):111-119.

[9] Sun L A.Closed-form solution of a Bernoulli-Euler beam on a viscoelastic foundation under harmonic line loads[J].Journal of Sound and Vibration,2001,242(4):619-627.

[10] 孙璐, 邓学钧. 移动的线源平稳随机荷载激励下梁的响应[J]. 力学学报, 1997, 29(3): 365-368.

SUN Lu, DENG Xue-jun. Random response of beam under moving random load in the line source form[J]. Acta Mechan ICA Sinica, 1997, 29(3):365-368.

[12] 周华飞, 蒋建群, 张土乔. 移动荷载下Kelvin地基上无限长梁的稳态响应[J]. 浙江大学学报(工学版), 2004, 38(10):1328-1333.

ZHOU Hua-fei, JIANG Jian-qun, ZHANG Tu-qiao. Steady-state response of infinite beam on Kelvin foundation under moving loads[J]. Journal of Zhejiang University(Engineering Science), 2004, 38(10):1328-1333.

[13] 李韶华. 重载汽车-路面-路基耦合系统动力学研究[D].北京：北京交通大学, 2008.

[14] 李皓玉. 车辆与路面相互作用下路面结构动力学研究[D]. 北京：北京交通大学，2010.

[15] Garg N, Thompson M R. Structural response of LVR flexible pavements at Mn/RIAD Project[J]. Journal of Transportation Engineering, 1999, 125(3):238-244.

[16] 张军. 重型车辆与刚性路面结构的动力相互作用理论分析和试验研究[D]. 长沙: 湖南大学, 2003.

[17] 王晅,张家生,杨国岳,等. 重载作用下公路路基及基层动应力测试研究[J]. 振动与冲击, 2007, 26(6): 169-173.

WANG Xuan, ZHANG Jia-sheng, YANG Guo-yue, at al. Test on dynamic stress of roadbed and pavement under heavy loads[J]. Journal of Vibration and Shock, 2007, 26(6):169-173.

[18] 李德葆, 陆秋海. 工程振动试验分析[M]. 北京:清华大学出版社, 2004.