一种宽带阵列数字下变频与均衡器一体化设计
贾可新, 柳桃荣,刘振华
(中国电子科技集团公司第三十八研究所,合肥 230088)
一种宽带阵列数字下变频与均衡器一体化设计
贾可新, 柳桃荣,刘振华
(中国电子科技集团公司第三十八研究所,合肥 230088)
从基本FIR均衡器的原理出发,讨论了不同系统采样率对均衡性能的影响。为适应宽带阵列中高速信号处理的要求,讨论一种经典的数字下变频和均衡器的设计方法。该方法虽然实现简单,但没有充分考虑采样率对均衡器设计的影响,需要大量的乘法资源。为了在保证均衡性能的同时降低系统对乘法资源的消耗,提出了一种数字下变频与均衡器的一体化设计方法。与传统方法相比,所提方法在阵列通道个数较大时能明显降低对乘法资源的损耗。通过仿真和实测数据分析,验证了所提方法的正确性。
FIR均衡器;数字下变频;宽带数字阵列
0 引 言
随着雷达、通信、对抗等领域对宽带系统的需求不断增加,宽带数字阵列处理技术被广泛应用。宽带数字阵列接收和发射都采用数字波束形成技术,控制波束的加权都是在基带实现的,这就要求信号在各通道内传输是无失真的,即各阵元通道的频率特性是一致的。然而实际系统中,由于诸如频率源、功放、混频器、滤波器和A/D变换器等模拟器件的存在,不可避免地引入宽带幅相误差。实际宽带系统由于时间、温度和环境改变以及器件老化也会引起通道间不同频点处幅相误差的变化。这种通道之间各频点处幅相不一致性(通道失配)将严重影响数字波束形成的性能[1-2]。
对于宽带数字阵列系统,为了补偿通道间频率响应的失配,可在每个通道中串联一个数字FIR均衡滤波器,使得所有通道的频率响应一致[3-4]。在实际系统中,为降低实现复杂度,传统设计方法通常将数字FIR均衡器串联到宽带数字下变频器之后。当系统输入信号采样率超过FPGA正常工作所允许的最高时钟频率时,数字FIR均衡滤波器通常采用多相滤波的思想在FPGA中实现。这种设计方法并没有考虑到采样率对均衡性能的影响,当阵列接收或发射通道个数较大时将消耗大量的乘法资源。
为了在保证均衡性能的同时降低系统对乘法资源的损耗,本文在讨论FIR滤波器的基本原理基础之上充分考虑采样率对均衡性能的影响,提出了一种数字下变频与FIR均衡器一体化设计方法。与传统方法相比,所提出的方法能够在保证均衡性能的同时明显地降低乘法资源的消耗。仿真数据分析验证了所提方法的正确性。
1 FIR均衡器的基本原理
假定宽带数字阵列系统中共有 个接收通道,如图1所示。在通道均衡时,校正源产生覆盖整个通带的宽带信号,经数字上变频(DUC)和D/A变换、射频前端后,从天线和接收射频前端之间同时耦合到各接收通道。均衡系数计算单元利用接收到的校正数据计算均衡系数,并将其加载到均衡器中。
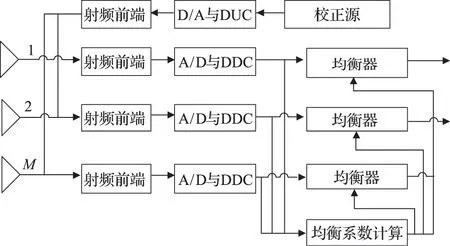
图1 宽带数字阵列的通道均衡示意图
均衡系数的计算方法如下[5]:
以通道1作为参考通道,其接收到宽带信号的频率响应为Gref(ω),其余通道接收到数据的频率响应为Gi(ω),i=2,…,M。为了保证通道间频率特性一致性,在通道中插入N阶FIR均衡滤波器,其频率响应为Hi(ω),i=2,…,M。设FIR均衡器的抽头延时为△,则有
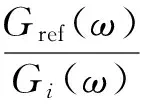
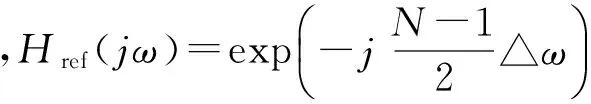
由于存在测量误差、计算误差以及不可避免的噪声,所以采用最小二乘拟合法来逼近H(ω),使得最佳权矢量满足如下方程:
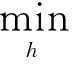
其中,W为加权对角矩阵,b为列矢量,即
A为DFT频率因子阵,即
其中,K>N为FFT点数。A为列满秩矩阵,故滤波器系数的最小二乘解为
根据奈奎斯特抽样定理,令B为待均衡带宽,△=1/fD为DDC输出采样率fD的倒数,则带宽时间乘积B△<1。由文献[6]可知,带宽时间乘积B△的取值大小对均衡器的性能(以剩余幅度失配和剩余相位失配作为衡量指标)影响很大。对于给定的均衡阶数N,当B△由0增大到1时,剩余幅度失配和剩余相位失配都是先逐渐减小,经过一个最小值(即为最佳值)后再逐渐增大,B△的选择有一个最佳范围,在0.35~0.65之间。
2 DDC与均衡器的传统设计
在宽带数字阵列系统中,按照传统的模块化设计思想,信号处理流程如图2所示。经A/D采集后,任何一路接收信号si(n)都须通过数字下变频,均衡滤波器模块,将宽带信号变换到基带,并补偿通道间的幅频和相频响应误差,为后续的波束形成和其他信号处理操作作准备。为讨论方便,这里假设宽带系统的采样率等于1 GHz,系统处理带宽为400 MHz,数字下变频输出采样率为500 MHz。
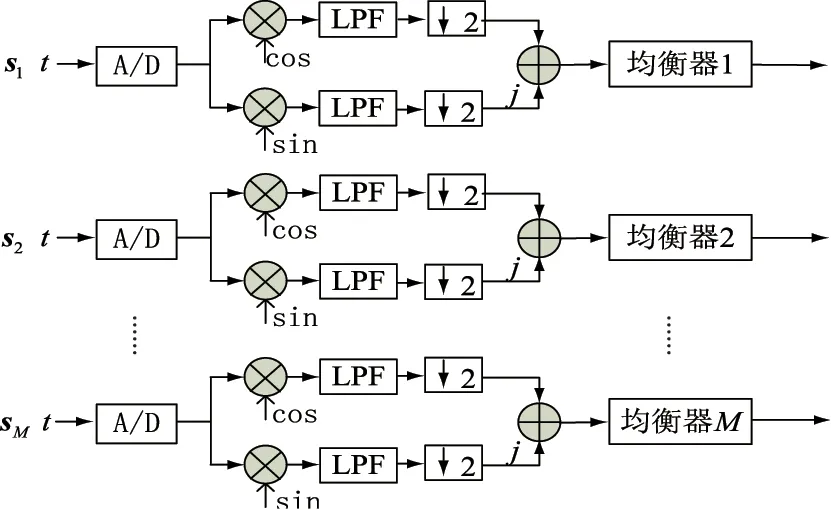
图2 DDC与通道均衡器的传统处理流程图
数字下变频模块主要包括正交混频器、数字控制振荡器(NCO)和低通滤波器。在宽带系统中,为降低乘法资源使用量,通常选择A/D的采样率fs和NCO的载波频率f0满足[7]:f0=3fs/4或f0=fs/4,此时NCO输出正弦和余弦信号是由1、0、-1、0交替数据组成的信号,这将使得正交混频的实现不需要乘法器。设低通滤波器的阶数为N,均衡滤波器的阶数为Ne,则低通滤波器每秒钟要实现500 M×2×N个实数乘法操作。均衡滤波器的系数为复数,每秒钟需实现500 M×Ne×4个实数乘法操作。
若存在M个接收通道,则低通滤波器每秒钟要实现500 M×2×N×M个实数乘法操作,均衡滤波器每秒钟要实现500 M×Ne×4×M个实数乘法操作。若在实际实现中,采用多相滤波器实现结构,FPGA中乘法器的工作时钟为250 MHz,低通滤波器与2倍抽取采用多相滤波结构实现,则低通滤波器每秒钟实际要实现250 M×2×N×M个实数乘法操作。均衡滤波器每秒钟要实现250 M×Ne×4×M×2个实数乘法操作。
3 DDC与均衡器的一体化设计
为完成数字下变频和通道均衡,传统的模块化设计思想会消耗过多的FPGA乘法资源,且未考虑采样率对通道均衡性能的影响。故本节考虑将数字下变频与均衡器进行一体化设计,在保证均衡器性能的同时降低FPGA资源的使用率。
为了在节省FPGA资源的同时提高均衡器的性能,将均衡滤波器前置于两倍抽取因子之间,如图3所示。在图2中均衡器位于抽取之后,其带宽时间乘积为0.8,而图3中均衡器前置,使得时间带宽积减小至0.4。由文献[6]可知,当均衡器阶数相等时,图3所示的均衡器具有更佳的均衡性能。
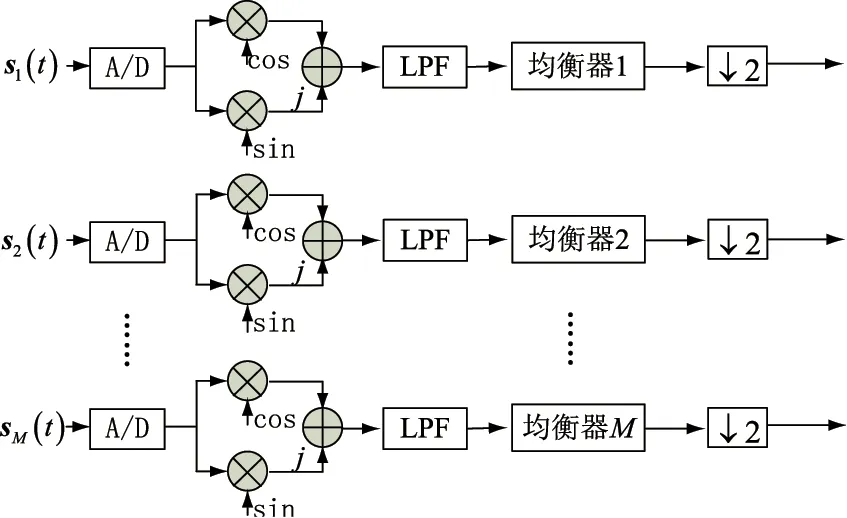
图3 数字下变频和均衡器一体化处理流程图
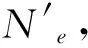
综合以上讨论,传统设计方法与一体化设计方法所使用的乘法资源个数之比为
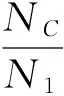
4 性能分析
4.1 乘法资源分析
对于传统设计方法,当N=48、Ne=40时,每秒钟乘法操作个数随通道数M的变化曲线如图4所示。随着通道个数的增加,均衡器消耗的乘法资源明显高于低通滤波器。
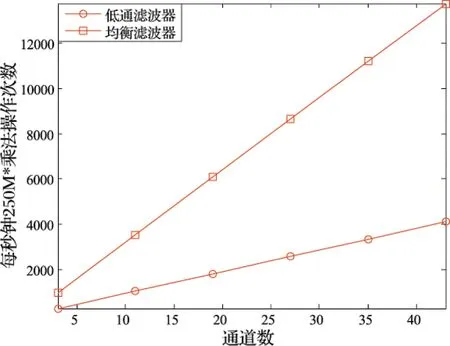
图4 不同通道下低通滤波器和均衡
4.2 均衡性能验证
实验一: 考虑两个接收通道,第一个通道作为参考。均衡前,第二通道的幅频响应和群迟延如图6所示。
令时间带宽积分别为0.4和0.8,均衡器阶数在36~72之间变化。经500次仿真实验,均衡后的剩余幅度失配误差和相位失配误差如图7所示。由图7可知,当均衡器阶数相同时,本文所提的一体化设计方法具有更佳的均衡性能。
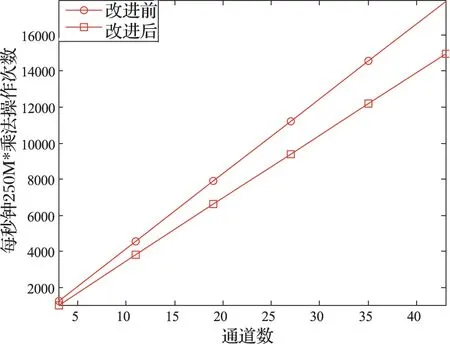
图5 两种设计方法的滤波器乘法运算次数对比图
实验二:实测数据包括4个接收通道,时间带宽积等于0.4,以第一个通道作为参考。均衡前,其他通道相对于参考通道的幅频响应和相频响应如图8所示。
当均衡滤波器阶数为32时,幅度失配误差的均值非常接近于零,标准差最大为0.3632 dB。相位失配误差的均值非常接近于零,标准差最大为2.3399°。所有通道均衡后的幅频响应和相频响应如图9所示。由图9可知,本文所提方法具有较好的均衡性能。
5 结束语
本文首先讨论了宽带阵列系统中一种经典的数字下变频和均衡器的设计方法。该方法相对简单,便于实现,但当阵列收发通道个数较大时需要大量的乘法资源。为了降低系统对乘法资源的需求,保证均衡器性能,考虑采样率对均衡性能的影响,提出了一种数字下变频和均衡器一体化设计方法。在性能分析中,比较了本文讨论的两种设计方法的乘法资源消耗情况。分析结果表明,本文提出的方法能明显地降低对乘法资源的损耗。最后通过仿真和实测数据分析,验证了所提方法的正确性。
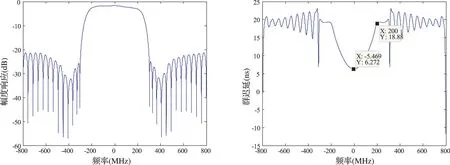
(a) 幅频响应 (b) 群迟延
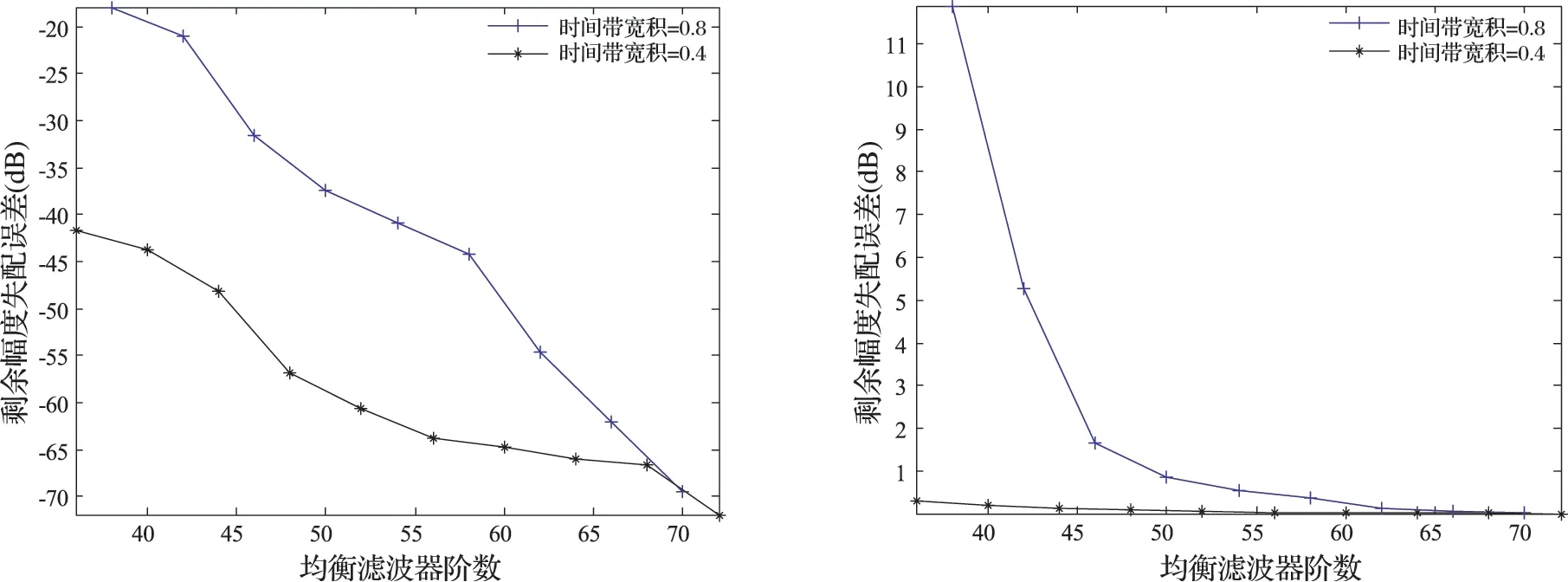
(a) 剩余幅度失配误差 (b) 剩余相位失配误差

(a) 幅频响应 (b) 相频响应
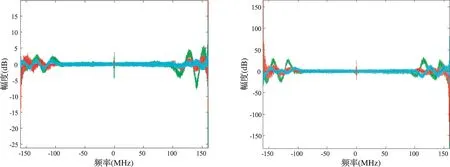
(a) 幅频响应 (b) 相频响应
[1] 张林让, 保铮, 张玉洪.通道响应失配对DBF天线旁瓣电平的影响[J]. 电子科学学刊, 1995, 17(3): 268-275.
[2] 吴曼青. 数字阵列雷达及其进展[J]. 中国电子科学研究院学报, 2006, 1(1):11-16.
[3] 吴洹, 张玉洪, 吴顺君. 用于阵列处理的自适应均衡器的研究[J]. 现代雷达, 1994, 16(1):49-56.
[4] 龚耀寰.自适应滤波-时域自适应滤波和智能天线[M]. 2版. 北京:电子工业出版社, 2003:308-333.
[5] 贾可新,柳桃荣,刘振华. 一种宽带阵列通道均衡器设计[J]. 航天电子对抗, 2013, 29(16):62-64.
[6] 王永良, 丁前军,李荣锋. 自适应阵列处理[M].北京:清华大学出版社, 2009:299-328.
[7] 杨小牛, 楼才义,徐建良. 软件无线电原理与应用[M].北京:电子工业出版社, 2001:8-57.
An integrative design of wideband array DDC and equalizer
JIA Ke-xin, LIU Tao-rong, LIU Zhen-hua
(No.38 Research Institute of CETC, Hefei 230088)
Based on the basic principle of the FIR equalizer, the effects of the sampling rates of different systems on the performances of the equalizers are discussed. To meet the demands of high-speed signal processing in the wideband array, a classical method of the digital down converters (DDCs) and the equalizers is designed and discussed. This method can be easily implemented, but it does not take the effects of the sampling rates on the equalizers into full consideration and needs many multipliers. To reduce the loss of the multipliers and ensure the performances of the equalizers, an integrative method of the DDCs and the equalizers is proposed. Compared with the conventional methods, the proposed method can obviously reduce the loss of the multipliers in the case of numerous array channels. The validity of the method is verified through the simulation and data analysis.
FIR equalizer; digital down converter; wideband digital array
2014-08-29
贾可新(1982-),男,工程师,博士,研究方向:雷达和对抗领域信号处理;柳桃荣(1968-),女,高级工程师,研究方向:雷达和对抗领域信号处理;刘振华(1983-),男,工程师,博士,研究方向:无线通信系统。
TN957.51
A
1009-0401(2014)04-0031-05

