基于STFT与WVD的雷达信号分析检测方法

王美玲,杨承志,吴宏超

(空军航空大学,长春 130022)

基于STFT与WVD的雷达信号分析检测方法

王美玲,杨承志,吴宏超

(空军航空大学,长春 130022)

对未知LFM雷达信号进行参数估计是截获分析、分选识别及干扰实施敌方低截获概率雷达信号的前提。本文分析了雷达信号参数检测方法WVD,并对该方法在对雷达信号检测时产生的交叉项引入了STFT线性变换进行处理。仿真实验表明,该方法在充分发挥了WVD对信号的分析处理能力的同时能有效地抑制交叉项影响。

WVD ；交叉项；STFT

0 引 言

在现代电子战环境,信号日益密集,且随着新雷达的不断投入使用,给电子侦察、干扰等电子对抗手段带来更加严峻的考验。低截获概率雷达因采用复杂调制波形和脉间波形捷变等技术,发射低截获概率、低辨识概率特征的雷达信号已成为目前电子对抗领域的研究热点。作为其中的一种非平稳信号,线性调频(LFM)信号具有大的时间频带积,高的抗干扰能力,是目前低截获概率雷达系统中应用最为广泛的一类脉冲压缩波形。对未知LFM雷达信号进行参数估计,是截获分析、分选识别及干扰实施敌方低截获概率雷达信号的前提。因此,对LFM信号检测分析方法进行研究具有重要意义。

在检测信号时,WVD方法有着非常高的分辨率,但难于避免交叉项干扰。针对这一问题,较早提出的方法有Cohen方法,在频域进行平滑,该方法在消除干扰项的同时也消除了信号项；模糊域方法对信号的适应能力较差,学者提出了自适应的核函数滤波方法以提高信号的适应性,但自适应方法需要信号的先验知识。为此本文在分析研究了STFT和WVD方法对信号进行时域分析各自优缺点后,提出了以WVD为基础,利用它对非平稳信号分析时的时频聚焦性,结合STFT在处理多信号分析时的线性特征,进行交叉项抑制,最终获得高的时频聚焦信号时频分布,提高了信号的检测性能[1-3]。

1 LFM信号模型

LFM信号的复解析表达式为

(1)

其中,rect(u)为矩形函数,u(t)是信号的复包络,τ是脉冲宽度,u为信号瞬时频率的变化斜率,f0为发射频率。LFM信号的时域波形和幅频特性如图1所示。

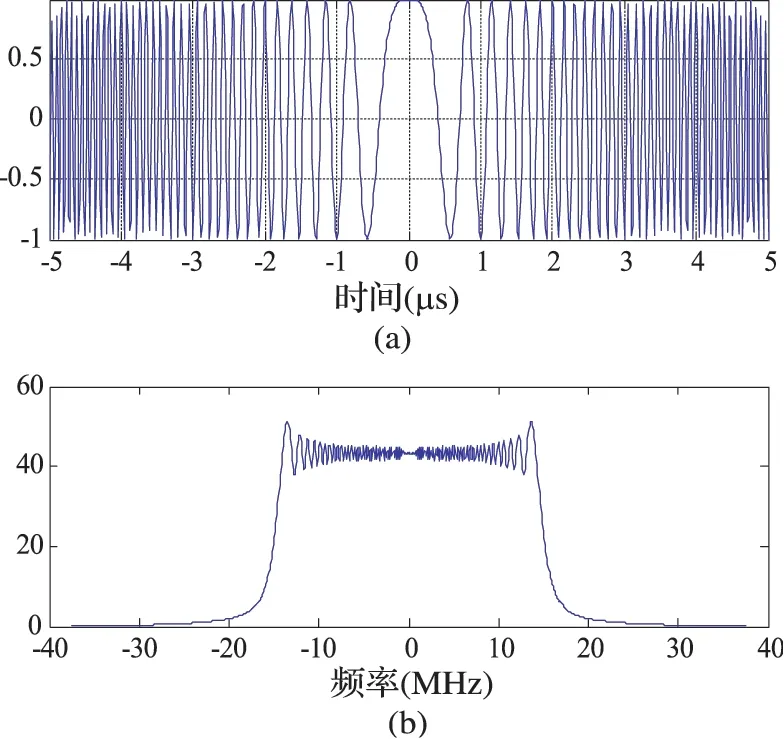
图1 LFM信号的时域波形(a)和幅频特性(b)

多分量的LFM信号可以表示为

(2)

其中,Ai为第i分量的幅度项；øi为向量项；f0i为频率项；K为调频斜率项参数,K=B/T。

2 Wigner-Ville时频分布(WVD)

Wigner-Ville分布最初由Wigner在量子学领域内提出,后由Ville引入到信号分析中,是一种最基本的非线性表示。信号s(t)的Wigner-Ville分布定义为

(3)

WVD具有很好的时间、频率分辨率,对于LFM信号WVD具有良好的时频聚集性。设LFM信号为

(4)

可得

W(t,f)=δ(f-kt-f0)

(5)

通过上式可以看出,LFM信号的WVD分布的幅值集中出现在表示信号的瞬时频率变化率的直线上,即沿着直线f=kt+f0的冲击线谱。图2给出了一个线性调频信号的WVD,可以清晰地看到信号的时频特性。

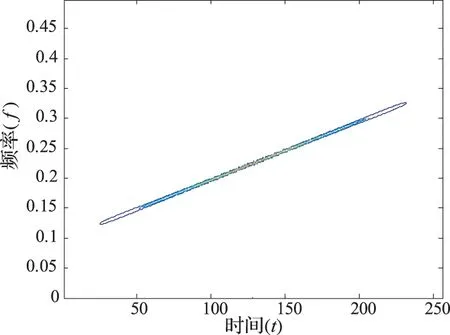
图2 线性调频信号的WVD

设

s(t)=s1(t)+s2(t)

(5)

可知

(6)

且

(7)

由上式可知,WVD可以看作是信号时间自相关函数的傅里叶变换,由于它是信号的二次时频,在对多信号进行时频分析时,WVD存在严重的交叉项。目前已有的许多时频分析方法基本都是在多分量交叉干扰项抑制和保持信号时频聚集性之间进行折中。实际上,即使是单分量信号,WVD也存在自身干扰项。

3 短时傅里叶变换(STFT)

给定一个时间宽度很短的窗函数g(t),令窗函数g(t)在t轴上滑动,则信号x(t)的短时傅里叶变换定义为

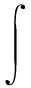
(8)

该式的物理意义是,信号x(t)在时间t的短时傅里叶变换就是信号x(t)乘以一个以t为中心的“分析窗”g(τ-t)所作的傅里叶变换,如图3所示。STFTx(t,f)既是时间的函数又是频率的函数,如图4所示,为STFT所处理的单个线性调频信号的时频图。

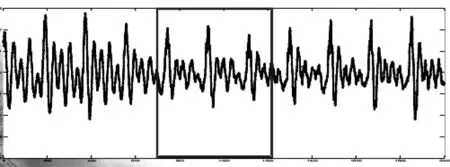
图3 STFT的窗函数

图4 线性调频信号的STFT

STFT是信号的线性表示,本身不存在交叉项的干扰,适用于多分量信号分析,其分辨性能很大程度依赖于窗函数类型及窗宽的选择。实际中被考察信号一般都是非平稳的,但STFT假定在窗函数宽度内信号近似平稳,其窗函数类型通常选择低通型窗函数,如高斯窗、汉宁窗等。窗函数一旦选定,其时频聚集性也就随之确定。根据不确定原理,窗函数时宽和带宽不可能同时达到任意小,因此其时频聚集性不佳。对于非平稳信号,STFT无自身干扰项,但聚集性较差,而WVD的聚集性较好,但存在的自身干扰项已经使信号本身无法清晰分辨[4-5]。

4 STFT与WVD分析方法

为了使分析简单化,将输入信号定义为只有两个信号的合成,即S(t)=S1(t)+S2(t),分别作WVD和STFT可得

W11(t,w)+W22(t,w)+2Re{W12(t,w)},

S11(t,ω)+S22(t,ω)

其中Re{W12(t,w)}是交叉项,会产生“虚假信号”,因此需要进行抑制。如果LFM信号存在多个分量,分量之间的交叉项会使得时频平面变得模糊不清,假如是在信号比不高的场合,很难发现各个分量的。短时傅里叶变换(STFT)绝对值的平方称之为谱图,采用谱图分析信号时,不能同时获得好的时间分辨率和频率分辨率。谱图属于二次时频分布,避免不了交叉项的干扰,但只要信号分量间有足够的间隔,交叉项就趋于零,也可以说谱图具有很差的时频聚集性。WVD是信号能量在时频面上的两维分布,具有较好的时频凝聚性,但受交叉项和噪声影响比较严重,由STFT获得的谱图没有交叉项,但是分辨率有限。因此,本文提出了基于WVD和SFTF雷达信号检测算法,把由WVD方法所获得的信号的时频图进行滤波,设定阈值,进行二值化。即设定一个阈值T,用T将图像的数据分成两部分：大于T的像素群和小于T的像素群。将谱图也进行二值化。将数字化的时频分析图和谱图进行图像融合,得到去掉干扰项的时频分布图。

5 仿真结果验证

设定多分量LFM,本文选取3个LFM信号进行实验,并分别用WVD分布、短时傅里叶(STFT)及基于WVD和STFT方法对多分量LEM信号进行仿真实验,以验证本文所给出结论。图5为WVD分布所示时频图,可以看出3个LFM信号频率随时间变化的特征。仿真结果表明,用WVD方法处理完的多分量信号存在明显的交叉项。图6为短时傅里叶的时频表示,经

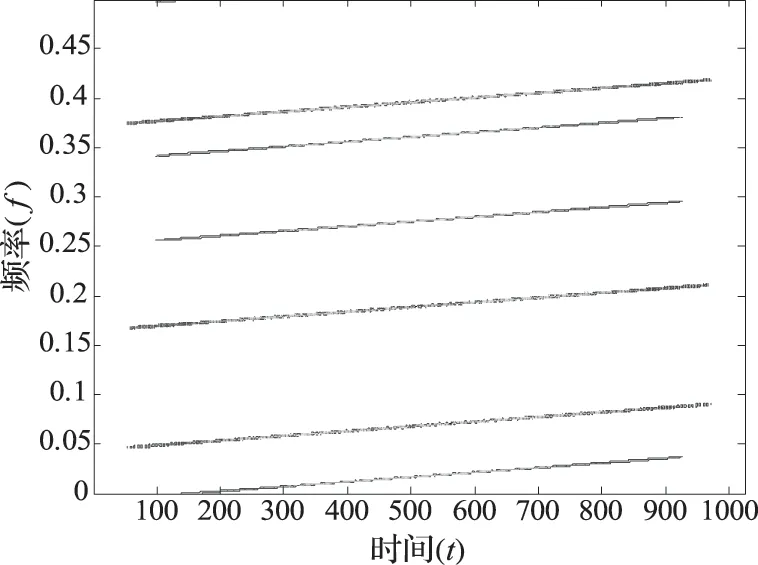
图5 线性调频信号的WVD

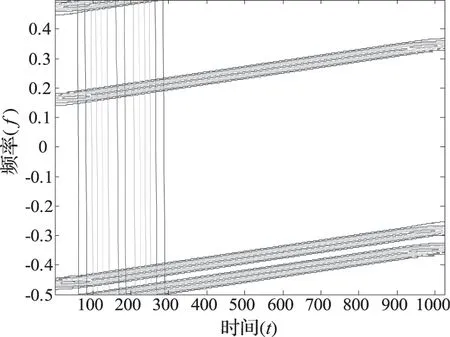
图6 线性调频信号STFT

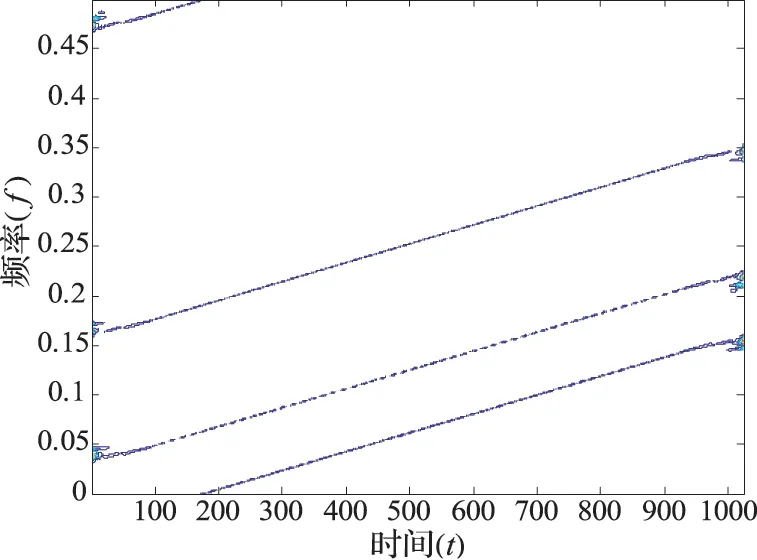
图7 线性调频信号WVD和STFT

过它处理的信号聚集性较差。图7为本文提出的基于WVD和SFTF方法处理后的时频图,可以看出在保持了较高的分辨率条件下消除了交叉项。

[1] 张贤达.现代信号处理[M].北京:清华大学出版社,2002.

[2] 李亚安,王军.自适应核时频分析在抑制交叉项中的应用[J].系统工程与电子技术,2004,26(11).

[3] 张贤达,保铮．非平稳信号分析与处理[M]．北京：国防工业出版社,1998.9：153-185.

[4] 张葛祥,胡来招,金炜东.雷达辐射源信号脉内特征分析[J].红外与毫米波学报,2004,23(6):477-480.

[5] 赵拥军,黄杰.雷达信号细微特征时频分析法[J].现代雷达,2003,25(12):26-28.

Radar signal analysis and detection method based on STFT and WVD

WANG Mei-ling, YANG Cheng-zhi, WU Hong-chao

(Aviation University of Air Force, Changchun 130022)

The parameter estimation of the unknown LFM radar signals is a prerequisite for the interception and analysis, the sorting and identification and the hostile low-interception probability radar signal jamming. The radar signal parameter detection method WVD is analyzed, and the cross terms caused by the WVD in radar signal detection are processed through the linear transform of the STFT. The simulation test indicates that this method makes full use of the signal analysis and processing capabilities of the WVD, and at the same time effectively suppresses the effects of the cross terms.

WVD; cross term; STFT

2014-07-17；

2014-07-21

王美玲(1985-),女,硕士,研究方向：机务质量控制；杨承志(1974-),博士,研究方向：电子对抗及信号处理；吴宏超(1982-),硕士,研究方向：信号分析处理。

TN957.51

A

1009-0401(2014)04-0036-03