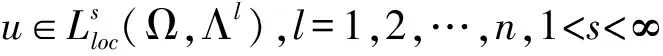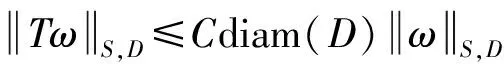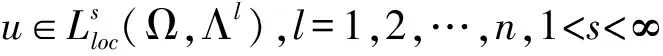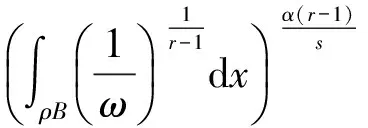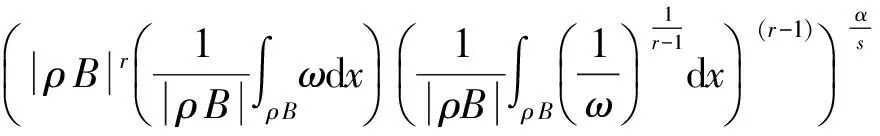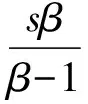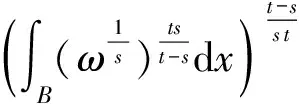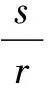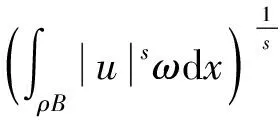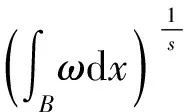复合算子的单权Poincaré-型不等式

贺 丹

(黑龙江工程学院 数学系，黑龙江 哈尔滨 150050)

复合算子的单权Poincaré-型不等式

贺 丹

(黑龙江工程学院 数学系，黑龙江 哈尔滨 150050)

首先建立作用于光滑微分形式的复合算子T·G的Poincaré-型积分不等式，其中算子T为同伦算子，G为格林算子。在此基础上，利用A-调和方程解的相关性质及结果，给出作用于非齐次A-调和张量的复合算子T·G的单权Poincaré-型积分估计式。

非齐次A-调和方程；微分形式；双权函数；积分不等式

定义1权函数ω(x)是子集E⊂Rn上的Ar(Ω)-权函数，r>1，如果ω(x)>0a.e.，并且有

对B⊂Ω成立，记为ω∈Ar(Ω)。

只有一个函数的权函数称之为单权函数，而对于有两个函数的权函数称之为双权函数。

引理1如果ω∈Ar，则存在与ω无关的常数β>1和C，使得对任意的B⊂Rn都成立

定义2当1

G∶Lp(ΛlM)→W2,p(ΛlM,μ)∩H⊥，

G(ω)=Ω(ω)-H(ω),

则知G是W2,p(ΛlM,μ)中的有界线性算子。

引理2令u是Ω⊂Rn上的一个A-调和张量，σ>1,0

(1)

成立，其中B是M中满足σB⊂Ω的球或矩形。

引理3令u∈C∞(Ω,Λl),l=1,2,…,n, 且1

(2)

(3)

对所有球体B⊂Ω成立。

由B⊂Ω且Ω是有界区域，式(3)可改写为

(4)

由式ω=d(Tω)+T(dω),对任何微分形式u有如下分解

u=d(Tu)+T(du).

(5)

结合式(4)及(5)，可得

(6)

由引理3知存在常数C3,C4>0，使得式(7)成立

且

(7)

则由式(4)～(7)可得

证毕。

下面对定理1进行推广，从而得到如下加权Poincaré不等式。

(8)

对所有满足ρB⊂Ω球体B成立。α是一个实数，且0<α≤1。

(9)

(10)

由不等式(9)及(10)得

(11)

(12)

把式(12)代入式(11)，得到

(13)

注意到ω∈Ar(Ω)，则有

(14)

把式(14)代入式(13)，可以得到

至此完成了0<α<1时情形的证明。

下面证明α=1时，定理2依然成立。由引理知，存在β>1,C7>0，使得式(15)成立

(15)

(16)

(17)

应用广义Hölder不等式，得到

(18)

又知ω∈Ar(Ω)，由此得

(19)

综合式(16)～(19)，得到

证毕。

[1]J HEINONEN, T KILPELAINEN, O MARTIO. Nonlinear Potential Theory of Degenerate Elliptic Equations[M]. Oxford, 1993.

[2]王友军, 沈尧天. 一类含临界指数双调和方程变号解的存在性[J]. 应用数学, 2009,22(2):37-40.

[3]许兴业.Rn上带奇异性的非线性双调和方程的正整解[J]. 数学物理学报,2009,29(1):32-38.

[4]C B MORRY. Multiple Integrals in the Calculus of Variations[J]. Spring-Verlag, Berlin,1966.

[5]G H HARDY, J E LITTLEWOOD. Some Properties of Conjugate Functions[Z]. J.Reine Angew.Math,1932,167:405-423.

[6]J B GARNETT. Bounded Analytic Functions[M]. New York：Academic Press, 1970.

[7]陈晓珊, 易法槐. 用Fourier变换求解上半平面的双调和方程[J]. 华南师范大学学报:自然科学版,2008(4): 25-29.

SingleweightedPoincaré-typeinequalitiesforthecompositeoperator

DAN He

(Dept. of Mathematics, Heilongjiang Institute of Technology, Harbin 150050, China)

First it establishes the Poincaré-type integral inequalities for the composite operator T·G acted on smooth differential forms. Operator T is homotopy operator and G is Green’s operator. On the basis of this, using the properties and results on estimates for the A-harmonic equations, the single weighted Poincaré-type integral estimates are obtained for the composite operator T·G acted on the non-homogeneous A-harmonic tensors.

non-homogeneous A-harmonic equation;differential form;two-weight function;integral inequality

2013-06-21

贺 丹(1980-)，女，讲师，研究方向：微分方程.

O175.2

A

1671-4679(2014)01-0078-03

郝丽英]