基于拓扑预测模型的船舶纵摇运动预报

赵 爽，安宇芳，王慧敬

(1.黑龙江工程学院 数学系，黑龙江 哈尔滨 150050；2.哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)

基于拓扑预测模型的船舶纵摇运动预报

赵 爽1,2，安宇芳1，王慧敬1

(1.黑龙江工程学院 数学系，黑龙江 哈尔滨 150050；2.哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)

针对船舶纵摇运动系统的灰色特性，利用拓扑预测法与GM(1,1)模型，研究船舶在海浪中非线性纵摇运动的预报问题，分别建立船舶纵摇运动的拓扑预测模型和船舶纵摇运动的GM(1,1)模型。根据实测船舶纵摇运动数据的特点，探讨拓扑预报模型的阈值选取方法。仿真结果表明:采用拓扑预测模型对船舶纵摇运动预报研究是合理且可行的。

船舶纵摇运动；拓扑预测模型；GM(1,1)模型；阈值；预测

船舶在航行时，经常产生六自由度的非线性随机运动，这是受到海浪等随机干扰作用而造成的。六自由度的运动[1]包括横摇、纵摇、摇艏、横荡、纵荡、垂荡。尽管可以通过船舶减鳍系统[2]对某几种运动进行减摇，但是对于纵摇运动还未寻到一种有效的减摇措施。目前，国内外对船舶纵摇运动姿态预报的研究方法主要有统计预报法[3]、卷积方法[4]、卡尔曼滤波法[5]、多层递阶预报模型[6]等。

灰色预测是灰色系统理论的重要组成部分,是解决信息不完备系统的预测，主要通过对原始数据列的预处理弱化其随机性，以此建立动态方程进行对系统行为仿真和预报。由于具有对已知数据信息的要求不高、易操作等特点，故早已被应用于诸多领域中。此预测包括数列预测法、季节灾变预测法、拓扑预测法、系统预测法等[7]。而船舶纵摇数据的波动幅度较大，呈现规律性差，符合灰色拓扑预测法的特点。因此，考虑船舶纵摇运动的灰色特性，本文将拓扑预测模型引入到船舶纵摇运动预报中，建立基于拓扑预测法的船舶纵摇运动预报模型。

1 灰色拓扑预测模型

灰色拓扑预测是对变化不规则的行为数据列的整体发展趋势的预测，有时也称波形预测[8]。其基本思想是在充分分析已知数据特点的基础上，进行预处理和选取阈值，建立GM(1,1)模型群，再对整个发展趋势进行预测。其模型的实施步骤如下：

1)选取一组原始数据列

X(0)=(X(0)(1),X(0)(2),…,X(0)(n)).

在二维平面内连接这n个数据点，得到原始数据列的曲线；

2)根据原始数据列X(0)的特点，取一系列阈值ξi(i=1,2,…,m)，使得minX(0)≤ξi≤maxX(0)，其中minX(0)、maxX(0)分别是X(0)的最小值和最大值。

(1)

5)利用最小二乘法计算式(1)中参数ai和ui，可得时间响应数列

(2)

6)由式(2)可得到时间响应数列进行累减还原

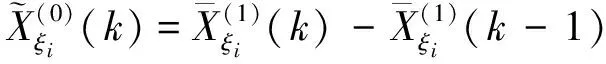
(3)

(4)

7)对预测数列进行精度检验。

2 船舶纵摇运动的拓扑预测模型

以某船舶实测的纵摇角度数据(1～43 s)为研究对象，运用灰色拓扑预测法建立模型，进行预测及精度检验。

2.1 阈值的选取

拓扑预测模型的建立，根据原始数据特点选择恰当的阈值是关键，这主要因为阈值在建模中的两个作用：一方面要确保GM(1,1)模型可以建立；另一方面尽可能确保所选阈值能充分反映原始数据的波形。根据船舶纵摇角度数据的振荡性特点，同时考虑到灰色预测GM(1,1)模型至少需要4个值，故选取一组非等距水平阈值，分别是ξ1=-1.86,ξ2=-1.7,ξ3=-1.578,ξ4=-1.375,ξ5=-1.172,ξ6=-0.969,ξ7=-0.766，ξ8=-0.563,ξ9=-0.36,ξ10=-0.157，ξ11=0.046,ξ12=0.249,ξ13=0.317,ξ14=0.452。

于是可得到水平阈值线与纵摇角度的原始数据折线的交点，如图1所示。

图1 船舶纵摇角度数据的曲线与阈值线相交

2.2 预测模型的构建

利用上述选取的14个非等距水平阈值，计算出其对应阈值线与原始数据折线的交点相对横坐标，得到新生成的14组序列：

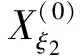
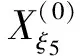
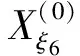
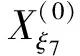
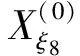
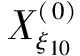
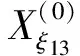
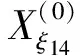
将上述序列组作为建立GM(1,1)模型群的原始数据，利用式(1)，建立相应的14个白化方程

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

2.3 预测模型的结果

依据所建立船舶纵摇运动的拓扑预测模型得到预测结果见表1。

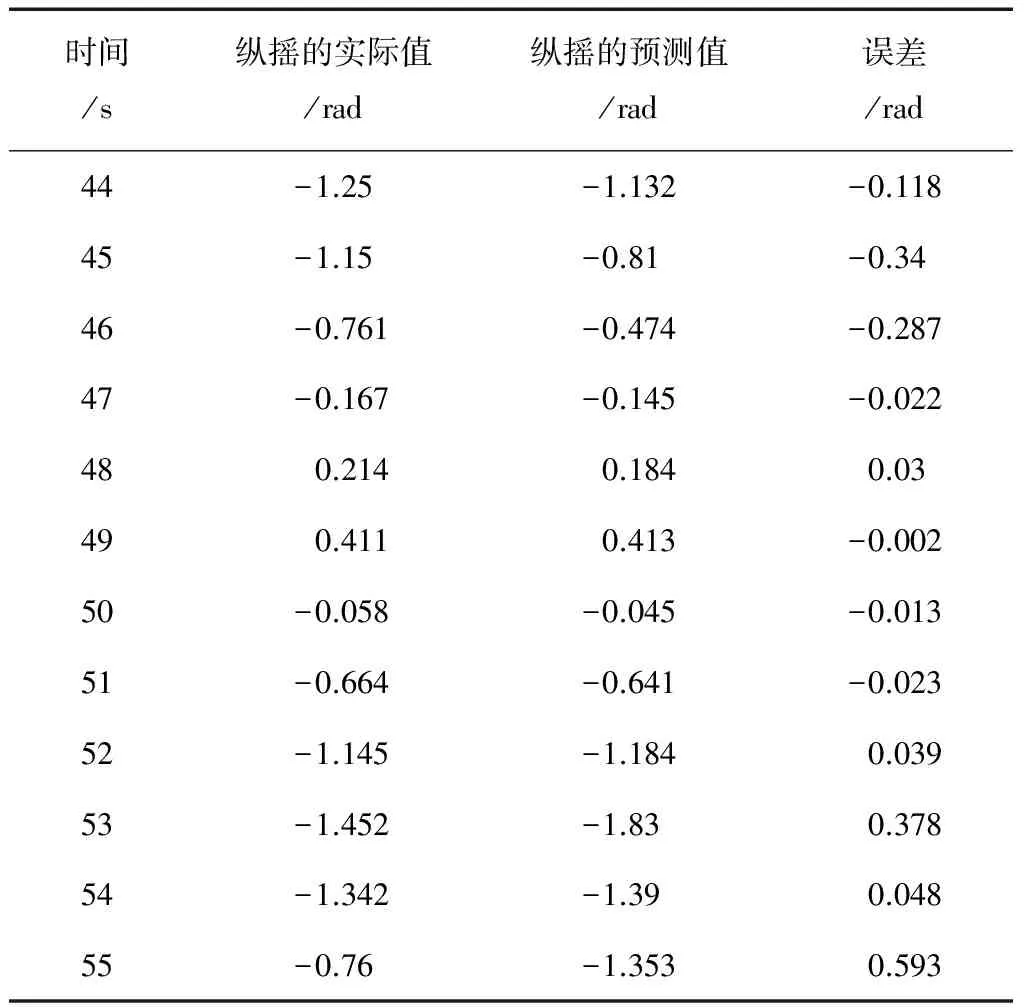
表1 船舶纵摇运动的拓扑模型预测结果

通过分析表1及图2可知，从t=44～54 s时段内(除个别时刻外)的预测误差精度相对较高，其误差基本在0.2°的量级上，此外，从t=44～55 s的12 s内的预测数据与实测数据符号一致，即船舶实际的纵摇方向与其预测方向是保持一致的。

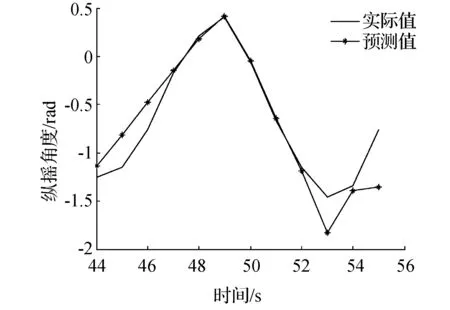
图2 船舶纵摇运动的拓扑模型预测结果

根据表1易得到预测时段内的平均误差，如表2所示。

表2 纵摇角度数据的平均预测误差

显然,从表2可知,该模型前12 s的预报结果还是可以接受,除预报时长2 s和3 s内的平均误差稍大外,其余平均误差基本在0.1°的量级上。

3 结果分析与对比

3.1 拓扑预测模型的误差分析

上述拓扑预测模型只给出了各时刻的误差和各预测时段内的平均误差，故再给出一种综合各时刻的整体平均误差——相对均方误差[9]。

定义1[9]称

(19)

是相对均方误差，其中,ε(k)是时刻k的模拟值的绝对误差，Amax为船舶纵摇角度数据所预测时段内的振幅最大值。

3.2 拓扑预测模型与GM(1,1)模型的对比

现仍以t=1 s到t=43 s时刻的纵摇角度数据为原始数据，建立船舶纵摇运动的GM(1,1)模型，预测结果如表3所示。

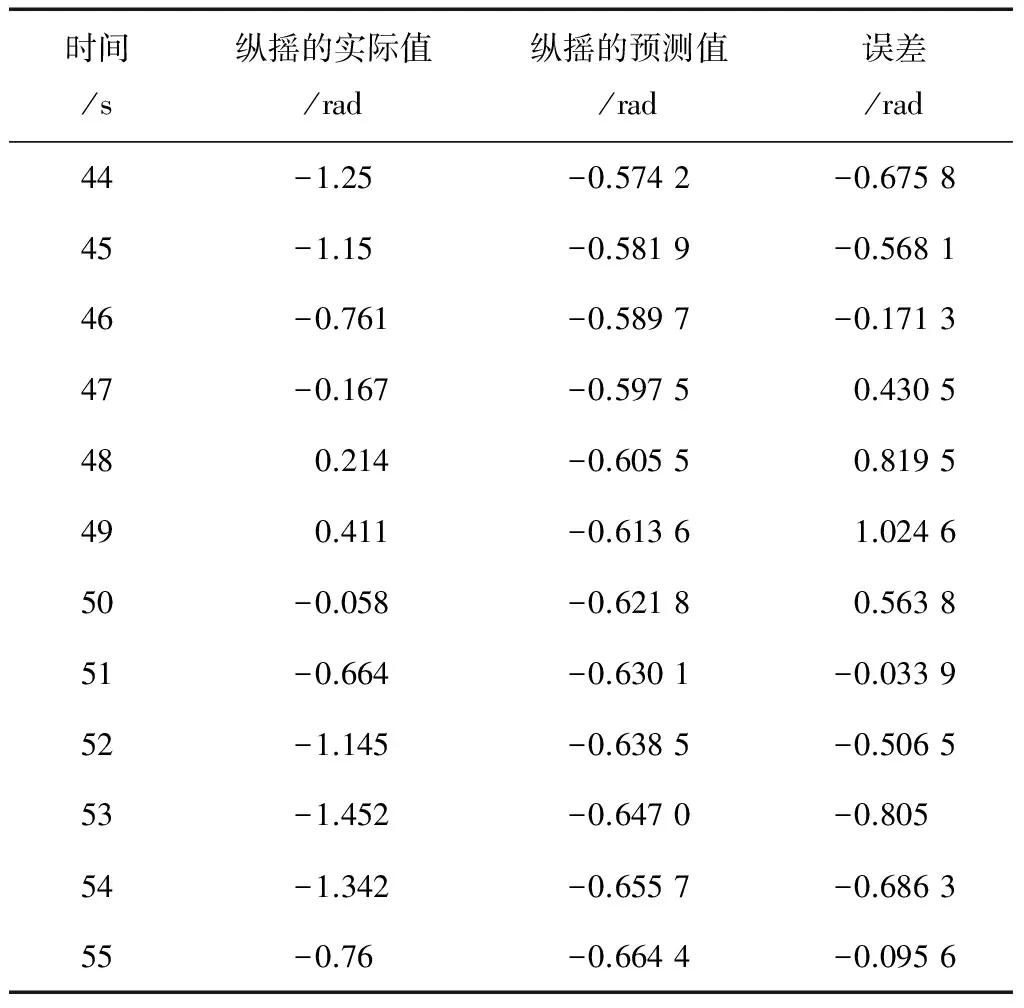
表3 船舶纵摇运动的GM(1,1)模型预测结果

从表3容易看出，灰色GM(1,1)模型各时刻的误差均比较大，计算得其11 s内平均误差是 0.571 4，而图3是由图2和表3画出的两种模型预测结果的对比图；从图3看出，拓扑预测法所得到的曲线的总体趋势与实际纵摇数据曲线大致吻合，呈现振荡的特征，而GM(1,1)模型得到的曲线呈单调下降的趋势，无振荡性，其主要原因在于GM(1,1)模型适合于非负单调递增的数据[10]，故GM(1,1)模型无法得到满意的预测结果。

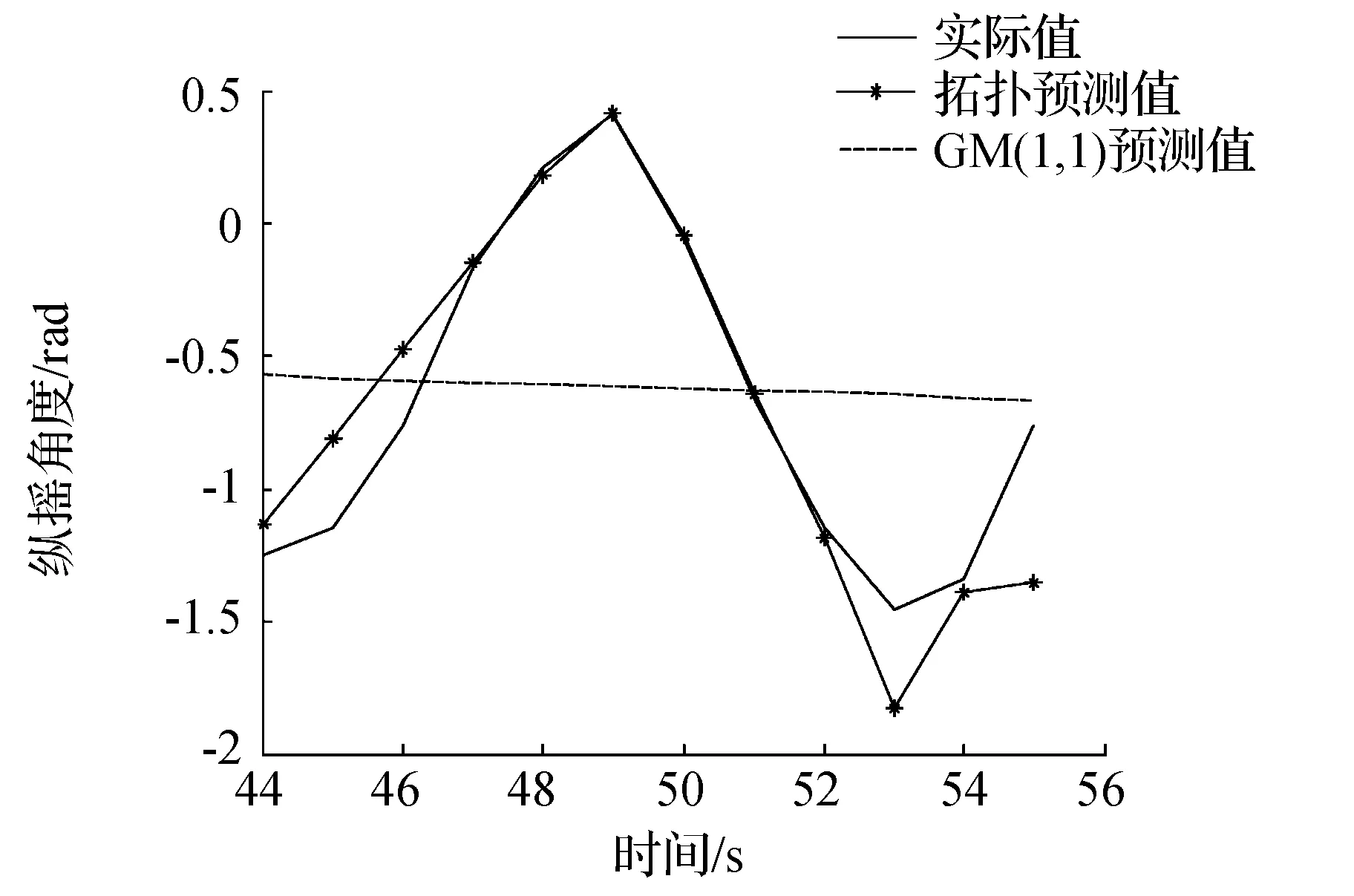
图3 两种模型预测结果的对比

4 结束语

本文针对实测船舶纵摇数据的特征，分别利用拓扑预测法和灰色GM(1,1)模型进行建模预测，仿真结果表明，灰色GM(1,1)模型预测值与原始数据相距较远，而拓扑预测模型基本上能预测出实测数据的发展走势，该模型在0.2°误差量级上可预测11 s，整体的相对均方误差为14.62%，预测趋势达12 s，说明基于拓扑预测模型的船舶纵摇预报是实用的。

[1]李积德.舰舶耐波性[M].哈尔滨：哈尔滨工程大学出版社, 2007.

[2]李晖.船舶减摇鳍系统智能控制及其可视化仿真的研究[D].大连:大连海事大学,2003.

[3]WIENER N. Extrapolation ，interpolation, and smoothing of stationary time series with engineering applications[M]. Cambridge MA: MIT Press, 1949：10-14.

[4]KAPLAN P. A Study of Prediction Techniques for Aircraft Carrier Motions at Sea[J]. Perforation of Arctic Sea-Ice Cover,1969,3(3):121-131.

[5]TRIANTAFYLLOU M, BODSON M. Real Time Prediction of Marine Vessel Motion Using Kalman Filtering Techiques[A]. Offshore Technology Conference(1982) [C].Texas: Offshore Technology Conference:1982.17-18.

[6]马洁,刘小河,李国斌.大型船舶纵摇运动的多层递阶预报[J].海洋工程, 2006,28(1):5-8.

[7]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京：科学出版社, 2004:163-165.

[8]李炎.更新MGM(1,n)模型及其在船舶运动姿态预报中的应用[D].哈尔滨：哈尔滨工程大学，2007.

[9]沈继红.灰色系统理论预测方法研究及其在船舶运动预报中的应用[D].哈尔滨：哈尔滨工程大学，2001.

[10]姜莉,王革新,任熹珍.哈尔滨市道路运输与经济发展水平预测分析[J]. 黑龙江工程学院学报:自然科学版, 2013,27(2):37-38.

Shippitchmotionpredictionbasedontopologyforecastingmodel

ZHAO Shuang1,2, AN Yu-fang1, WANG Hui-jing1

(1.Dept. of Mathematics, Heilongjiang Institute of Technology, Harbin 150050, China;2. Automation College, Harbin Engineering University, Harbin 150001, China)

Aimed at the grey characteristic of ship pitch motion system, the topology forecasting model and GM(1,1) model are applied to investigating the prediction problems in the nonlinear ship pitch motion in waves. Based on that, a topology forecasting model and GM(1,1) model of ship pitch motion are constructed respectively. According to the characteristics of the ship pitch motion data obtained from the laboratory experiment, a method of threshold selection is explored for the topology forecasting model. Simulations illustrate that the prediction of ship pitch motion is reasonable and feasible based on this topology forecast model.

ship pitch motion;topology prediction model;GM(1,1) model;threshold;forecasting

2013-08-02

黑龙江省教育厅科学技术研究项目(12521459)

赵爽(1984—)，女，讲师，博士研究生，研究方向：系统分析与建模.

N941.5

A

1671-4679(2014)01-0071-04

郝丽英]