AUTOCAD,SOLIWORKS,MATLAB 渐开线齿廓的精确绘制

杨春杰,姜 超

(湖北理工学院 机电工程学院,湖北 黄石 435003 )

AUTOCAD,SOLIWORKS,MATLAB渐开线齿廓的精确绘制

杨春杰,姜 超

(湖北理工学院 机电工程学院,湖北 黄石 435003 )

在齿轮零件的设计仿真中，常需要绘制渐开线齿轮的齿廓，但现有的各种计算机辅助设计软件不支持直接绘制渐开线齿廓，给齿轮的设计仿真造成了一定的局限。因此，提出了几种简便而实用的基于AUTOCAD、SOLIWORKS和MATLAB精确绘制渐开线齿廓的方法，所绘制的齿廓的精度可根据设计的需要进行调整，从而提高了齿轮零件的设计效率和仿真效果。

渐开线齿廓;精确绘制;CAD;SOLIWORKS;MATLAB

渐开线齿廓的精确绘制一直是齿轮绘制和仿真中的难点，现有的AUTOCAD、SOLIWORKS和MATLAB不支持直接绘出渐开线，一般是用圆弧近似代替渐开线，其缺点是不能形成系列化修改，也不能直接从图形中得出渐开线的相应数据[1]。因此，笔者提出了几种简单且易于操作的绘制渐开线齿廓的方法，其精度可以调整，并能满足大部分的设计和仿真需要。

1 AUTOCAD精确绘制渐开线齿廓

在CAD图形文件中建立新坐标系，以原点为圆心画半径为Rb的基圆，以10°为步长(步长越小，精确度越高)9等分第1象限圆弧，得交点A1、A2、……、A9，分别在交点上作圆的切线，并截取A1B1为一个步长(10°)的弧长，A2B2为2个步长(2×10°)的弧长， ……，A9B9为9个步长的弧长，在CAD的高版本中可以直接测出弧长，精确度可根据需要自行设置，然后用样条曲线顺次连接B1、B2、……、B9，即得基圆的渐开线，渐开线的绘制过程如图1所示。

图1 渐开线的绘制过程

确定齿数、模数和压力角后，算出分度圆半径R、齿顶圆半径Ra、齿根圆半径Rf，然后在图1上分别以R、Ra、Rf画圆，截得齿轮的渐开线齿廓的一侧，镜像后修剪得到完整的一个轮齿的渐开线齿廓，如图2所示。

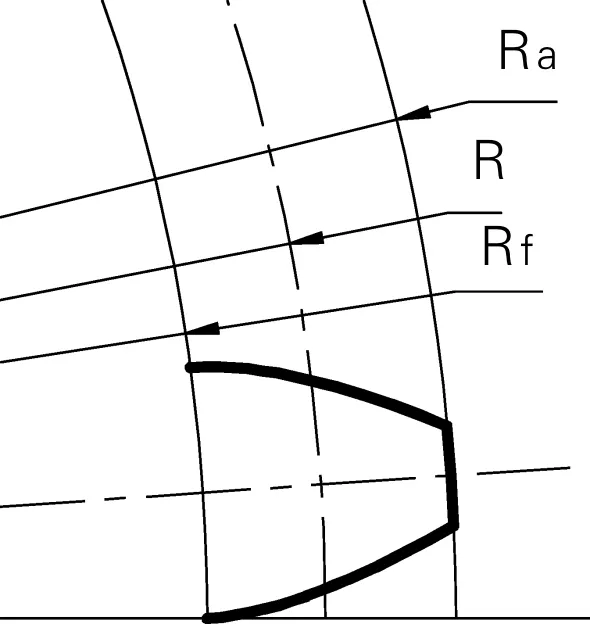
图2 渐开线齿廓

渐开线的形状只和基圆的大小有关。当绘制齿轮时，先根据齿数、模数和压力角计算出基圆的大小，再将图形整体缩放，使图1中半径为Rb的基圆尺寸等于所画齿轮的基圆尺寸。这样，此渐开线可以应用到任何参数的齿廓绘制中。在AUTOCAD中，可用环形阵列创建齿轮的轴向面域，再拉伸即可得到三维齿轮模型，渐开线齿轮模型如图3所示。

图3 渐开线齿轮模型

2 SOLIDWORK精确绘制渐开线齿廓

在SOLIDWORK中，用曲面放样生成渐开线的精度较高，也比较容易理解和绘制。在图1所得到的渐开线上取任意一点B，作基圆的切线，切点为A，连接OA，OA和X轴夹角为t(用弧度表示)得到渐开线函数关系图如图4所示。

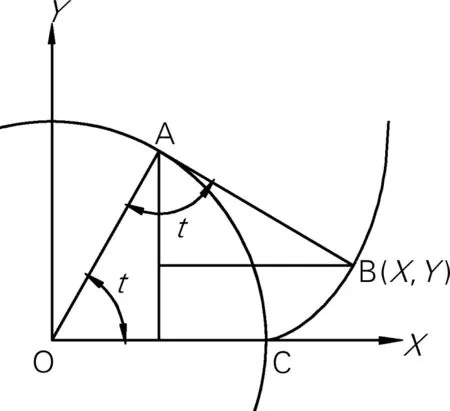
图4 渐开线函数关系图

根据几何关系得到下列方程：

(1)

由方程组(1)可知，渐开线坐标是夹角t的函数。当t在0°～90°之间时，以步长1°(转换成弧度值)取90个点，分别算出渐开线的90个坐标值，将得到的点连接起来就得到了精确的渐开线曲线。

SOLIDWORKS可以用渐开线的参数方程来画标准齿轮，以模数m=2，齿数z=30，压力角为20°的直齿轮为例说明方程式驱动的曲线画渐开线齿轮的方法。

齿轮尺寸参数为：分度圆直径D=mz=60mm；基圆直径Db=Dcos20°；齿根圆直径Df=m(z-2.5)=55mm；齿顶圆直径Da=m(z+2)=64 mm。

基圆直径用方程式标注,添加基圆直径方程式如图5所示，添加后并激活，标注尺寸后可得到齿轮的齿顶圆、齿根圆、分度圆和基圆。齿轮的各参数圆如图6所示。

图5 添加基圆直径方程式

在图6的基础上插入方程式驱动的曲线，选择参数性，输入渐开线的参数方程(1)，插入方程式驱动的曲线如图7所示，注意把角度转为弧度，最后可得渐开线如图8所示。

图6齿轮的各参数圆

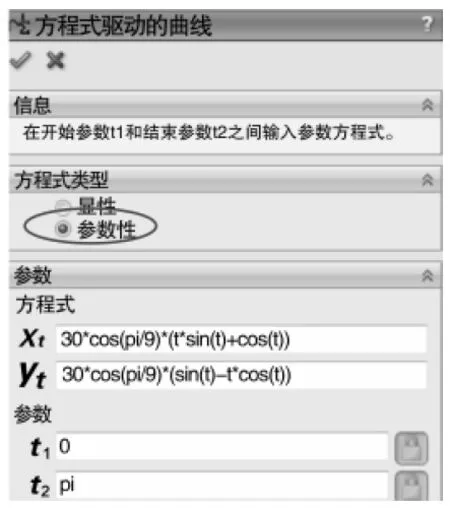
图7插入方程式驱动的曲线

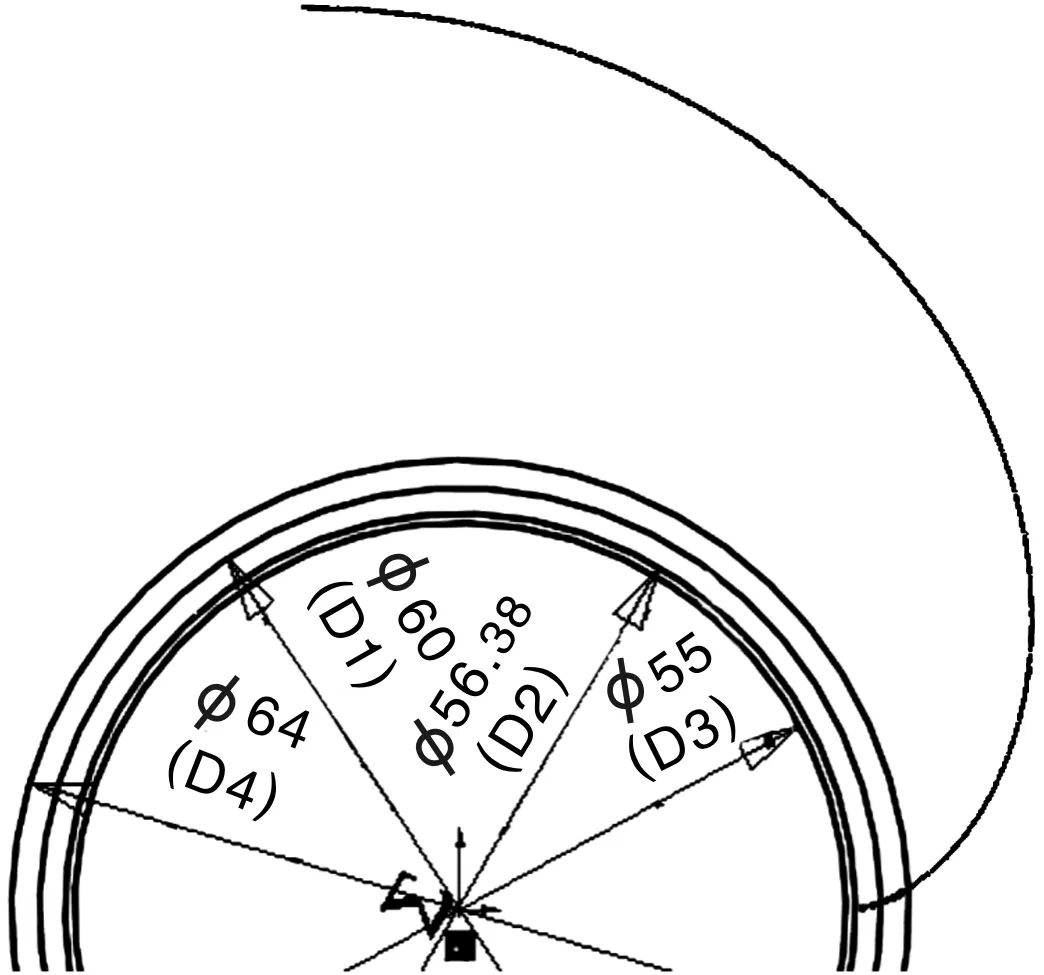
图8 渐开线

裁剪成所需的渐开线齿廓。标注尺寸后，原有的对称关系有可能会错乱，需要重新标注几何关系，在基圆与齿根圆之间加圆弧与齿根圆相切半径(0.25m)，标注完几何关系后使中心线水平以完全定义草图。与AUTOCAD中的方法一样，拉伸并阵列得到渐开线直齿圆柱齿轮模型。渐开线齿廓如图9所示。

图9 渐开线齿廓

由于SOLIDWORKS中的放样线条都是用一段一段的短线逼近的，如果将精度中小数点后的位数增加，获得的渐开线就会有极微小的差别。如果想获得更高精度的渐开线，可以使用程序法生成渐开线[2]，可在SOLIDWORKS中插入公式曲线宏运行，当关键点数为500个时，精度可以达到小数点后8位，如果还需要更高的精度，可适当添加关键点数。

3 MATLAB的渐开线齿轮的范成法仿真

一对齿轮啮合传动时，两轮的齿廓互为包络线。如齿轮刀具与毛坯模拟一对齿轮传动，则可加工出与刀刃互为包络线的齿廓。刀刃和齿轮齿廓均为渐开线。

如下为渐开线齿轮的范成动态模拟程序[3-4]。

hd=pi/180;m=2;

z=input('渐开线齿轮齿数z=′);

phi0=20;x=0;x0=0;y0=0;r=m*z/2;hd=pi/180;

du=180/pi;p=pi*m;

s=2.5*m*tan(phi0*hd);h=(2*s+p)/4;

c=x0-2*p-h;

x1(1,1)=c; y1(1,1)=-(r+(1.25+x)*m)+y0;

x1(2,1)=x1(1,1)+s;

y1(2,1)=y1(1,1)+2.5*m;

x1(3,1)=x1(2,1)+(p/2-s);

y1(3,1)=y1(2,1);x1(4,1)=x1(3,1)+s;

y1(4,1)=y1(3,1)-2.5*m;for i=5∶20

x1(i,1)=x1(i-4,1)+p;

y1(i,1)=y1(i-4,1);

end

j=0;

for d_phi=0:(6*hd):4.398226/2; j=j+1;for i=1:20;

x1(i,j)=x1(i,1)-r*d_phi;

y1(i,j)=y1(i,1);

s2=y1(i,j)-y0;s1=x1(i,j)-x0;

r1(i,j)=sqrt((s1)^2+(s2)^2);

phi(i,j)=atan(s1/s2);

x2(i,j)=r1(i,j)*sin(phi(i,j)-d_phi)+x0;

y2(i,j)=r1(i,j)*cos(phi(i,j)-d_phi)+y0;

end

end

for d_phi=0:-(6*hd):-4.398226/2; j=j+1;

for i=1:20;

x1(i,j)=x1(i,1)-r*d_phi;

y1(i,j)=y1(i,1);

s2=y1(i,j)-y0;s1=x1(i,j)-x0;

r1(i,j)=sqrt((s1)^2+(s2)^2);

phi(i,j)=atan(s1/s2); x2(i,j)=r1(i,j)*sin(phi(i,j)-d_phi)+x0;

y2(i,j)=r1(i,j)*cos(phi(i,j)-d_phi)+y0;

end

end %5.渐开线齿轮范成的动态模拟

figure(1);j0=j;

for j=1:j0

plot(x2(:,j),y2(:,j));

axis equal;hold on;grid on;

end

rb=r*cos(20*hd);ra=r+(1+x)*m;

rf=r-(1.25-x)*m; ct=linspace(0,2*pi);

plot(rb*cos(ct),rb*sin(ct),′r-′);

plot(r*cos(ct),r*sin(ct),′g′);

plot(ra*cos(ct),ra*sin(ct),′r′);

plot(rf*cos(ct),rf*sin(ct),′r′);

title('渐开线齿轮的动态模拟′);

xlabel(′m=2,z=30,alpha=20,x0=0′);

MATLAB生成的渐开线范成动态模拟结果如图10所示。

通过MATLAB程序完成齿轮齿廓的绘制,只需输入齿轮的基本参数便可完成范成仿真过程,生成的齿轮齿廓可以满足设计对精度的要求,任何基于此程序生成齿轮的研究都是可靠的。因此,在齿轮的设计、加工与检测过程中都起着重要的指导作用。

绘制渐开线齿廓并对齿轮进行仿真无论是在AUTOCAD、SOLIDWORKS还是在MATLAB等计算机辅助设计软件中都有很多的方法，本文所介绍的方法能够较精确地绘制渐开线齿廓，最为简便和实用，易于操作。而且，MATLAB的程序也可以调用到SOLIDSWORK中，进行宏运算以建立渐开线齿轮的仿真模型[5]；SOLIDSWORKS也可以调用AUTOCAD的图形文件进行编辑和处理[6]。只要熟悉其中一种软件的应用，都可以根据本文的方法精确绘制渐开线齿廓，并完成渐开线齿轮的设计和仿真。

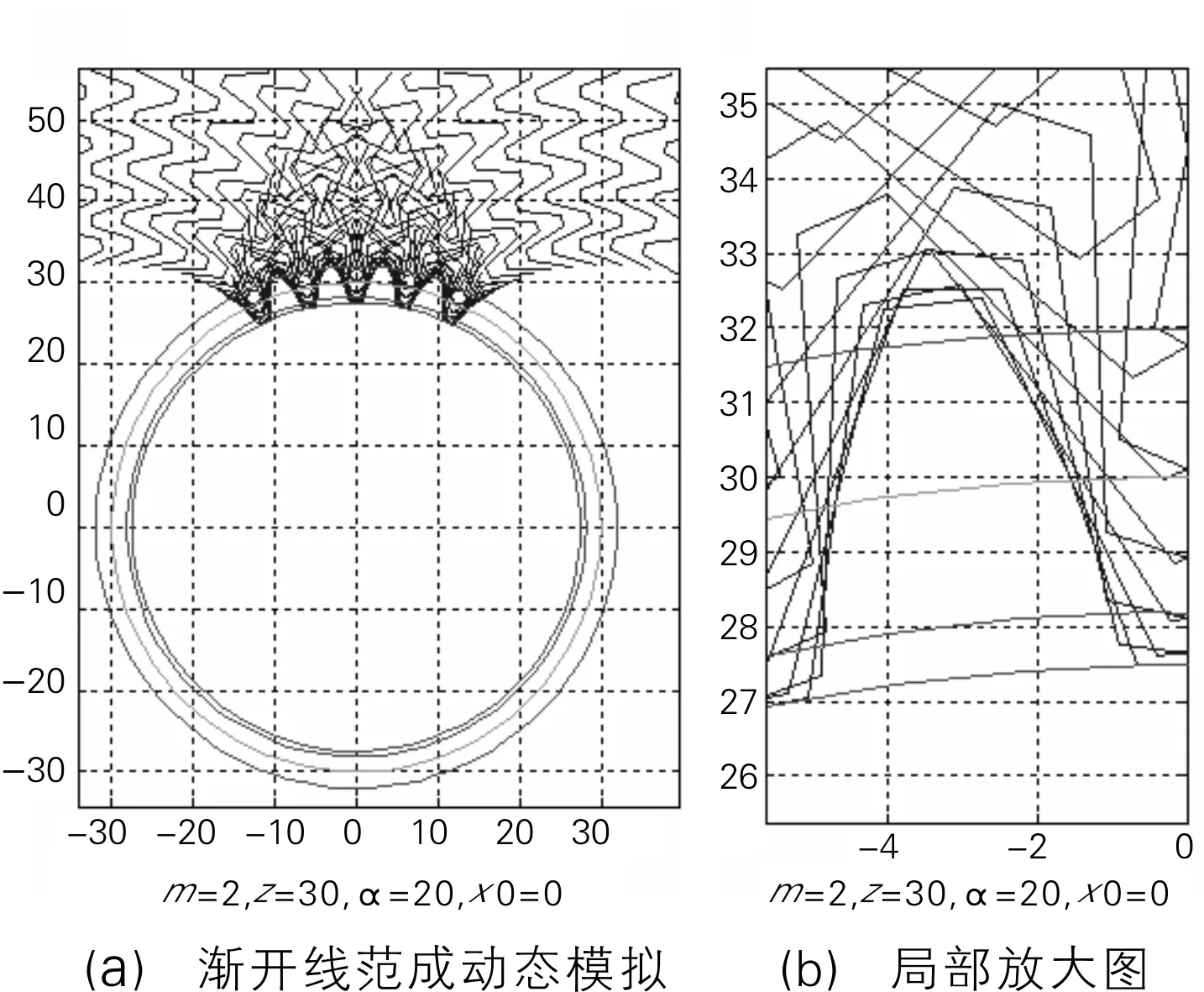
图10 渐开线范成动态模拟

[1] 郑旖,张为民.渐开线圆柱齿轮MATLAB建模及其有限元网格的自动划分[J].佳木斯大学学报，2012,30(6):844-848.

[2] 王素秋.基于Solidworks的齿轮库系统设计[J].科技信息,2010(6):261-263.

[3] 陈杰.MATLAB宝典[M].北京:电子工业出版社,2011：1.

[4] 昂雪野.基于AutoCAD渐开线齿轮范成仿真程序设计[J].长春理工大学学报,2008,31(4):138-139.

[5] 敖文刚.基于MATLAB的运动学、动力学过程分析与模拟[M].北京:科学出版社，2013:6.

[6] 北京兆迪科技有限公司.SolidWorks 曲面设计实例精解[M].北京:机械工业出版社,2013:3.

(责任编辑桂堤)

Precise Generation of Involutes Tooth Profile of Gear Based on AUTOCAD,SOLIWORKS and MATLAB

YangChunjie,JiangChao

(School of Mechanical and Electronic Engineering,Hubei Polytechnic University,Huangshi Hubei 435003)

Involutes tooth profile needs drawing in the design simulation of the gear parts,whereas not any software of computer aided design can draw the profile of gear directly,which brings limitation to the design simulation of the gear.The paper puts forward several simple and practical methods of precise generation of involutes tooth profile based on AUTOCAD,SOLIWORKS and MATLAB Software.The gear profile precision can be adjusted to satisfy the different design requirements,which improves the efficiency of design and effect of simulation.

involutes tooth profile;precision generation;CAD;SOLIWORKS;MATLAB

2014-02-28

杨春杰(1973— )，女，副教授，硕士，研究方向：计算机图形学、 虚拟设计与仿真。

10.3969/j.issn.2095-4565.2014.04.003

TH12

A

2095-4565(2014)04-0008-04