粗糙集理论在师范生培养质量分析中的应用

张 帆,李其深,刘 颖

(1西南石油大学 理学院,四川 成都 610500；2中南民族大学 数学与统计学学院,湖北 武汉 430074)

粗糙集理论在师范生培养质量分析中的应用

张 帆1,李其深1,刘 颖2

(1西南石油大学 理学院,四川 成都 610500；2中南民族大学 数学与统计学学院,湖北 武汉 430074)

师范生教育是高等本科教育体系的一部分，为初等教育培养高水平教育工作者和管理人才。基于粗糙集理论讨论师范生的培养质量问题。首先确定评价指标并随机抽取一定数量的数据，根据粗糙集的重要度对数据进行属性约简，通过约简表提取规则，对师范生培养质量进行客观评价分析，为以后的师范生培养提供参考。

粗糙集；属性约简；重要度；师范生；培养质量

0 引言

师范生教育是科教兴国和人才强国战略的重要内容。我国师范院校众多，以“德高为师，身正为范”为标准培养一代又一代的教育工作者。本文从评价的基本理论着手，将师范生的培养质量作为对象，构建师范生培养质量的评价体系，加强对师范生培养理论层次的认识。从实践操作的角度来看，建立科学高效的师范生培养质量评价体系可以推进我国师范生培养的规范发展和持续改进。对于师范生培养质量的讨论能够在一定程度上帮助教育系统从上而下整体地提高办学水平。

粗糙集理论[1-2]是一种用来处理不精确、不确定和不完全数据的非经典数学理论。粗糙集理论可以从大量的数据中挖掘潜在的、有利用价值的知识。粗糙集理论将知识理解成为“区分事物的能力”，将论域上的知识进行划分，通过论域上的等价关系来表示知识。对知识的这种特殊理解方式决定了它与传统的处理不确定性问题理论的方法存在着本质的区别。粗糙集理论不需要已知数据外的其他先验知识，通过对知识的简化和知识的依赖性分析，完全可以由已知的数据导出决策规则。由于粗糙集理论一般只能处理离散数据，所以当要处理连续属性值数据时，一般先要对数据离散化[3]。本文尝试借助粗糙集的理论与方法，对师范生的培养质量进行客观的数学理论方法的分析研究，并给出相应的决策规则，帮助高校在人才培养过程中更清晰地对师范生进行考核与教育。

1 预备知识

1.1粗糙集理论基础

粗糙集理论由波兰科学家Z.Pawlak于1982年提出，它是继概率论、模糊集、证据理论之后又一新的处理模糊和不确定性知识的数学工具[4]。粗糙集理论认为知识本身就应该具有对对象的分类能力，并提供严格的数学理论方法，使得知识有一个清晰定义的数学意义，并且可使用数学方法来分析处理。运用粗糙集理论能处理定量、定性的因素，有效分析不完整的、不一致的、不精确的等各种不完备的信息，能对数据进行分析推理，发现其中隐含的规律。其主要思想就是在保持知识分类能力不变的前提下，通过知识约简来导出问题的决策或分类规则。目前，粗糙集理论已经被成功地应用于过程控制、决策分析、机器学习、数据挖掘与模式识别等领域。

定义2 若P⊆R,且P≠Φ，则P中全部等价关系的交集称为P上的不可分辨关系，记为ind(p)：ind(P)={(x,y)∈U×U|∀q∈P,f(x,q)=f(y,q)}。

定义3 设S=(U,A,V,f)为一知识表达系统，A=C∪D,C∩D=Φ，C称为条件属性集，D称为决策属性集。具有条件属性和决策属性的知识表达系统称为决策表。

定义4 设S=(U,A,V,f)为一个信息系统，a∈A，如果ind(A-{a})=ind(A)，则称a在A中是不必要的，否则称a在A中是必要的。

定义5 设S=(U,A,V,f)为一个信息系统，如果∀a∈A在A中都是必要的，则称属性集A是独立的，否则称A是相关的。

定理1 如果A是独立的，P⊆A，则P也是独立的。

定义6 设S=(U,A,V,f)为一个信息系统，P⊆A，如果P是独立的，且ind(P)=ind(A)，则称P是A的一个约简。

定义7 设S=(U,A,V,f)为一个信息系统，A中所有必要属性组成的集合称为属性集A的核，记为core(A)。

定理2core(A)=∩red(A)，其中red(A)表示A的所有约简。

定义8 对于决策表S=(U,C∪D,V,f)中的条件属性集X⊆C,W⊆U，X的支持子集是SX(W)=W(U/X)-=∪V∈U/X,V⊆WV。

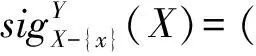
1.2指标体系的建立与数据离散化

师范生的培养质量主要通过师范生个体反映出来，作为培养师范生的高校，所采用的数字计划会对师范生培养质量有直接的影响[6-7]。学生的各项指标数据就是师范生培养质量优劣的具体表现，也是师范生培养质量的重点考核标准。本文根据师范生的教育目标和师范生的本质特点，考察和剖析师范生培养形成的全过程，建立以政治思想素质、专业课程学习、外国语水平、计算机水平、教学实践、学位论文为评价指标的评价体系。

在对学生指标数据离散化的过程中，指标的评价数据往往带有某种语义偏好，对于带有偏好的有关语言值评语集釆用等级制进行分类，并进行数值化。对于语义偏好由低到高，依次建立多个评价等级。语言值评语集的数值化表如表1所示。

表1 语言值评语集的数值化表

指标数据也常常带有连续数值，对于这种带有连续数值的指标数据，需要进行离散化。具体的方法是：将连续数值的整个区间按照划分的完整性依次分为4个区间，并对这4个区间的数值偏好关系进行离散化、数值化。连续数值的离散化表如表2所示。

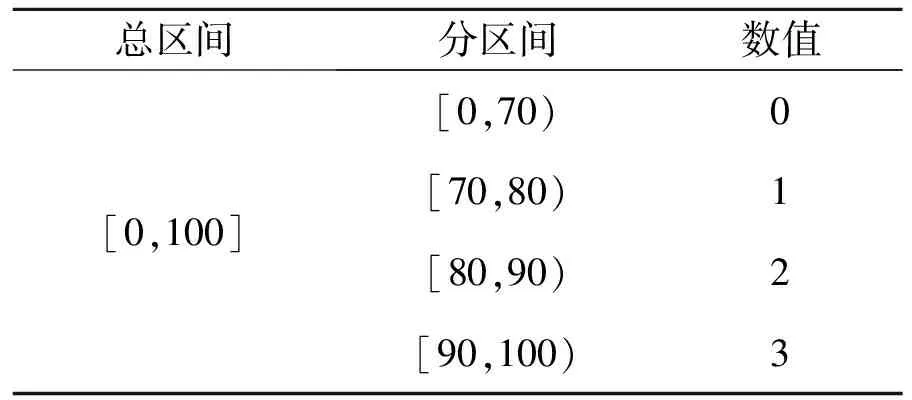
表2 连续数值的离散化表

2 评价指标对培养质量的影响分析

首先建立关于师范生培养的信息系统，即S=(U,C∪D,V,f)，其中，U={u1,u2,…,un},ui表示第i名学生，共有n名；以师范生培养影响指标作为条件属性C={aj,j=1,2,3,4,5,6}，a1表示政治思想素质，a2表示专业课程学习,a3表示外语水平,a4表示计算机水平，a5表示教学实践，a6表示学位论文。将培养质量作为决策属性，记为d，D={d}，d的取值为1、2、3、4,分别代表差、中等、良好、优秀；d的值由各班主任及专业教授主观给出。随机抽取学生原始数据如表3所示。

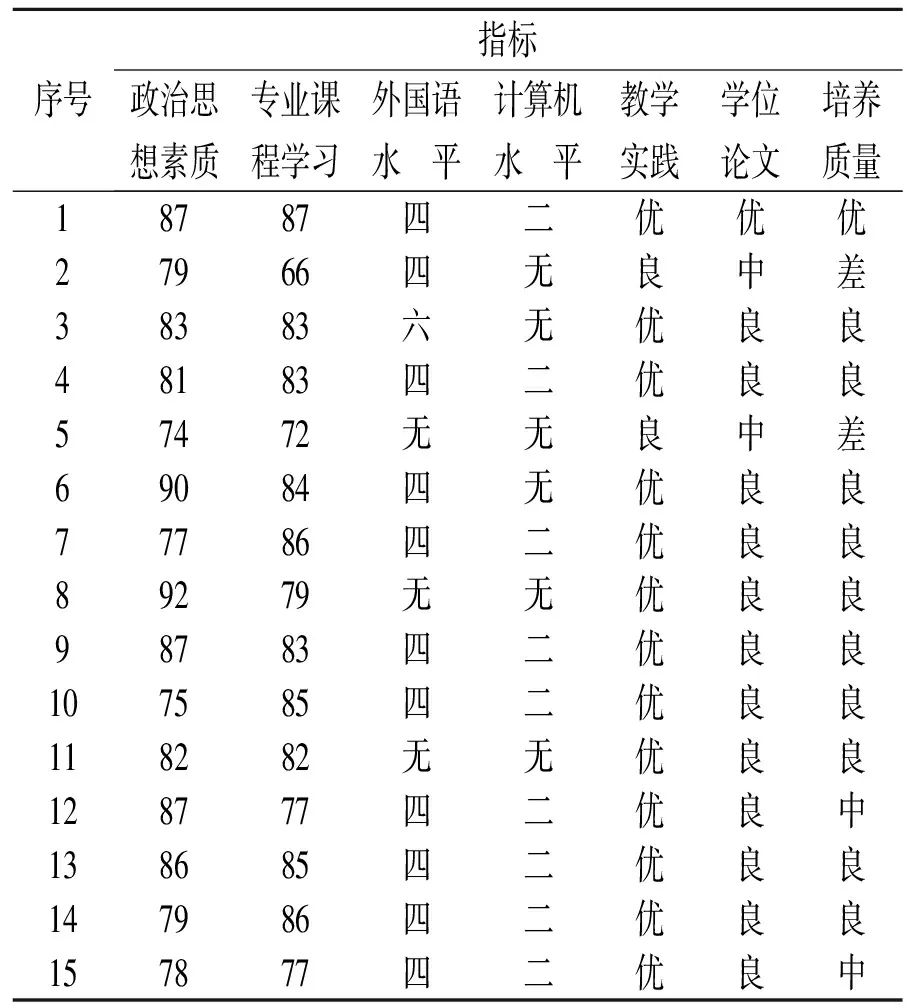
表3 随机抽取学生原始数据

按照表2中离散化数值表将决策表进行离散化后得到离散化处理后各指标数据如表4所示。

表4 离散化处理后各指标数据

基于属性重要度对以上决策表进行属性约简，该算法的具体步骤如下所示[8]：

1)求核算法。

输入：信息系统S=(U,C∪D,V,f)

输出：属性集合C的核core(C)

Step1：设置1→i；

Step3：令xi∈core(C)，转Step4；

Step4：如果i=|X|，则算法完成，core(C)即为属性集合C的核。如果i<|X|，转Step5；

Step5：令i+1→i，转Step2。

2)属性约简算法。

输入：信息系统S=(U,C∪D,V,f)

输出：属性集合C的核约简red(C)

Step1：根据求核算法求出core(C)；

Step2：令B=core(C)，如果ind(B)=ind(C)，转Step5；

Step3：∀a∈CB，计算它们相对于core(C)的属性重要度，取属性重要度最大的属性am，如果这样的属性有多个，则选取在论域上形成的划分个数最少的那个，把它加入B中，即B∪{am}⟹B；

Step4：如果ind(B)≠ind(C)，转Step3，否则转Step5；

Step5：输出B∈red(C)，算法结束。

通过算法进行数据处理得到的核是{a2,a6}，约简结果{a1,a2,a6}与{a2,a3,a6}与{a2,a4,a6}。对于约简{a1,a2,a6}得到属性约简表如表5所示。

表5 属性约简表

规则提取得到：

a1(2)anda2(2)anda6(3)⟹d(3)

a1(3)anda2(2)anda6(2)⟹d(2)

a1(2)anda2(2)anda6(2)⟹d(2)

a1(1)anda2(2)anda6(2)⟹d(2)

a1(3)anda2(1)anda6(2)⟹d(2)

a1(2)anda2(1)anda6(2)⟹d(1)

a1(1)anda2(1)anda6(2)⟹d(1)

a1(1)anda2(1)anda6(1)⟹d(0)

a1(1)anda2(0)anda6(1)⟹d(0)

从此约简得到的规则中可以得到以下信息：如果一个学生政治思想素质与专业课程学习良好、学位论文优秀，那么这个学生的培养质量是优秀的；如果一个学生政治思想素质不差、专业课程学习与学位论文良好，那么这个学生的培养质量是良好的；如果一个学生政治思想素质优秀、专业课程学习中等、学位论文良好，那么这个学生的培养质量是良好的；如果一个学生政治思想素质中等或者良好、专业课程学习中等、学位论文良好，那么这个学生的培养质量是中等的；如果一个学生政治思想素质与学位论文中等、专业课程学习较差或者中等，那么这个学生的培养质量是差的。对于其他约简表也可以提取相应的规则并得到培养质量的分析和参考。

3 结论

对于师范类学生来说，属性集{政治思想素质，专业课程学习，外国语水平，教学实践，学位论文}的约简为{政治思想素质，专业课程学习，学位论文}，{专业课程学习，外国语水平，学位论文}，{专业课程学习，计算机水平，学位论文}，属性集的核为{专业课程学习，学位论文}。说明专业课程学习、学位论文基本上可以反映出对学生的培养质量水平，而师范生特有的教学实践由于评价由所在实践单位给出，一般得到的评价都是优秀，没有客观反映实际教学效果，故从数据上得不到参考。通过规则表可以发现，培养一名优秀或者良好的师范生需要在哪些方面加强教育，在实际的教育培养过程中可以更清晰地了解他们的发展趋势并使他们变得更加优秀。

[1] Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences，1982，11：341-356.

[2] 张文修，吴伟志，梁吉业，等.粗糙集理论与方法[M].北京：科学出版社，2001:1-39.

[3] 王彪，段禅伦，吴昊，等.粗糙集与模糊集的研究及应用[M].北京：电子工业出版社，2008:1-32.

[4] 董婷.硕士研究生教育质量评价的研究[D].武汉:武汉理工大学，2005.

[5] 贺卫红，刘志辉，钟嘉鸣.基于粗糙集的教育网站综合评价研究[J].计算机应用与软件，2009(26)：57-61.

[6] 王丽娜.基于粗糙集的数据挖掘改进的属性约简算法研究[D].成都:电子科技大学，2012.

[7] 麦宏元.基于粗糙集的高职院校学生综合测评模式的应用研究[D].南宁:广西大学，2012.

[8] 张岩，秦克云，宋军智.基于粗糙集理论的研究生教育质量评价方法[J].文教资料，2012(3月下旬刊):136-138.

(责任编辑桂堤)

Application of Rough Set Theory in Analysis of Normal Students' Cultivation Quality

ZhangFan1,LiQishen1,LiuYing2

(1School of Science,Southwest Petroleum University,Chengdu Sichuan 610500;2School of Mathematics and Statistics,South-Central University for Nationalities,Wuhan Hubei 430074)

Normal education is a part of the higher undergraduate education system,which can train high-level educators and management personnels for primary education.This paper discusses the cultivation quality of normal stuednts based on Rough Set Theory.Firstly,the evaluation indexes and a certain amount of random data should be chosen.Then the data attribute reduction can be carried out according to the importance degree of rough sets.By using reduction table to extract certain rules, the training quality of normal students are evaluated and analyzed objectively,which provides a reference for the future training.

rough set;attribute reduction;significance;normal students;cultivation quality

2014-05-09

张帆(1990— )，男，硕士生。

10.3969/j.issn.2095-4565.2014.04.010

TP18

A

2095-4565(2014)04-0036-05