不满足A-R条件的双调和方程无穷多解的存在性

谢 华 朝

(河南财经政法大学 数学与信息科学学院, 郑州 450056)



不满足A-R条件的双调和方程无穷多解的存在性

谢 华 朝*

(河南财经政法大学 数学与信息科学学院, 郑州 450056)

在有界光滑区域Ω⊂RN(N>4)上, 研究了双调和方程Δ2u-λu=f(x,u),x∈Ω;u=∂u/∂n=0,x∈∂Ω,其中,f(x,u)是关于u的奇函数,u趋于无穷时是次临界的,并且不满足A-R条件.利用对称的山路引理,证明上面的方程有无穷多解且相应的临界值序列趋于正无穷大.

双调和方程; 无穷多解; A-R条件

1主要结果

本文主要研究如下双调和方程无穷多解的存在性:

Δ2u-λu=f(x,u),x∈Ω;

u=∂u/∂n=0,x∈∂Ω,

(1)

其中,λ是实数,Ω是RN(N>4)中包含零点的有界开区域且有光滑的边界∂Ω. ∂u/∂n指外法向导数.非线性项f(x,u) 满足下面的条件.

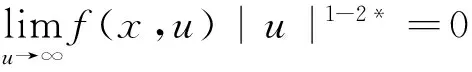
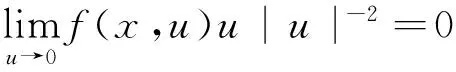
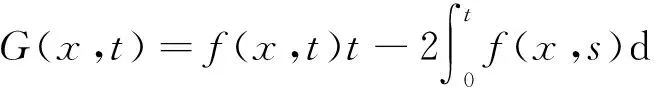
(f4)f(x,u)是关于u的奇函数.

双调和方程可以描述静态形式的光束变化或刚体的运动 (参见文献 [1]). 利用变分方法, 许多学者研究了在第一或第二边值条件下的非线性双调和方程. 文献[2]在有界光滑区域Ω中讨论了方程

Δ2u=λ|u|q-2u+|u|2*-2u,

(2)

其中,10;当x∈∂Ω时,u=∂u/∂n=0或u=Δu=0.利用亏格理论和Ljusternik-Schnirelmann方法, 证明了存在正常数λ0, 使得对任意的 0<λ<λ0, 方程(2)有无穷多解. 如果(2) 中的q=2 且λ≥0, 在一些特殊的区域, 文献 [3] 证明了方程解的存在性. 同时得到在球内, 正解是不存在的. 对于方程(1), 很多文献要求f(x,t) 满足A-R条件: 存在θ>p,对于任意的x∈Ω,

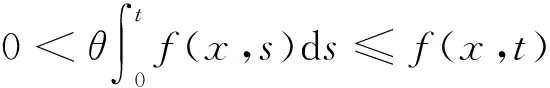
(3)

文献 [4-6]中,有许多有趣的结论.

定理1如果f(x,u)满足条件(f1)～(f4), 那么方程(1) 有无穷多解, 并且相应的临界值序列趋于正无穷.

2预备引理

引理1由条件 (f1) 知, 对任意的ε>0, 存在正数Cε>0, 使得

F(x,u)≤ε|u|2*+Cε,(x,u)∈Ω×R.

(4)

由 (f2) 知, 当u→0 时,F(x,u)=o(up). 存在θ>0 和M>0, 对任意的|u|≥M, 有

F(x,u)≥C|u|2+θ,f(x,u)u>0.

(5)

用反证法可得下面的引理2.

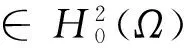
I(un)→c,I′(un)→0,

(6)

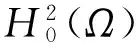
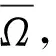
Sνj2/2*≤μj,

其中,δxj是xj点的Dirac测度.

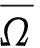
证明令任意的ε>0 充分小, 使得当i≠j时,Bε(xi)∩Bε(xj)=φ. 定义在 [0,+∞) 上的光滑截断函数ρ(t)满足0≤ρ(t)≤1. 当 0≤t≤1/2 时,ρ(t)≡1;当t≥1 时,ρ(t)=0. 记φj(x)=ρ(|x-xj|/ε), 则当|x-xj|<ε/2时,φj(x)≡1; 当|x-xj|≥ε时,φj(x)≡0. 更进一步, |φj|≤C/ε, |Δφj|≤C/ε2. 因此

(7)

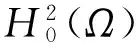
〈I′(un),unφj〉=∫|Δun|2φj+

2∫Δununφj+∫unΔunΔφj-

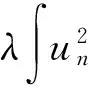
(8)

直接计算得

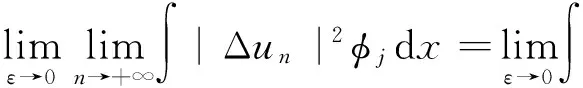
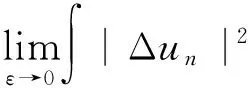
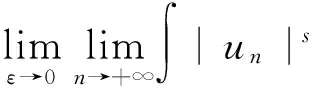
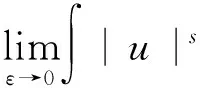
(9)

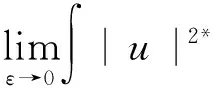
(10)

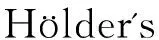
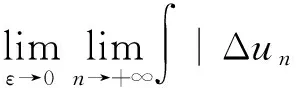
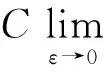
‖Δφj‖LN/2(Bε(xj))≤

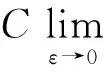
利用(f1)和(9)式可得

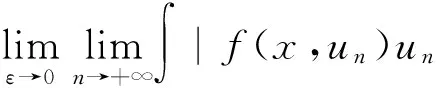
由上面的估计,(8)式化为

(11)

因此, 对于任意的j∈J,μj=0. 所以J是有限集.

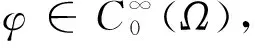
∫|φu|2*dx.

(12)

结合φun→φu得, 在L2*(Ωε)中,un→u;在L2N/(N-2)(Ωε)中,un→u.

由Lebesgue分解定理知

dμ=|Δu|2+dσ,

(13)

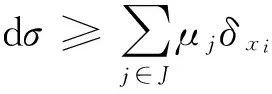
用标准的证法可得该引理.

3无穷多解的存在性

本节利用对称的山路引理, 证明定理 1.

引理6[8]假设泛函I满足下面的条件:

3) 对于j=1,2,…, 存在有限维子空间序列{Xj}, d(Xj)=j和常数rj>0. 若对任意的u∈XjBrj,有I(u)≤0, 则I有无穷多不同的临界点, 且相应的临界值是正的.

∫ΩF(x,u)dx≥

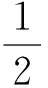
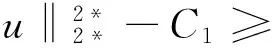
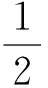
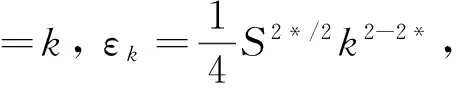
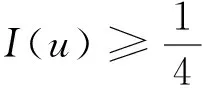
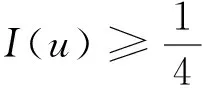
(14)

由于k→+∞时,λk→+∞, 取k0>0,使得 1/4-|λ|/(2λk+1)≥1/8, 且当k>k0时,k2>16C1. 因此

(15)

另一方面, 有限维空间Xk上的范数是等价的, 取R>max{M,[(1+|λ|)/C2]1/θ,k}, 则对任意的u∈XkBR, 结合(5)式得

I(u)≤(1+|λ|)‖u‖2-

C2∫{x∈Ω:|u|>M}|u|2+θdx-C′≤

(1+|λ|-C2‖u‖θ)‖u‖2-C′≤0.

由引理6知I有无穷多不同的临界值.

若不存在映射φ, 则γ(A)=+∞; 若A=Φ, 则γ(A)=0. 记

注1在定理1相同的条件下, 同样可以证明带Nevier边值条件的双调和方程:

Δ2u-λu=f(x,u),x∈Ω;

u=Δu=0,x∈∂Ω

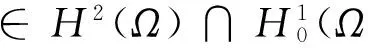
注2上面方程中如果f(x,u)=|u|q-2u+|u|r-2u(2

[1] Lazer A,Mckenna P. Large amplitude periodic oscillations in suspension bridges: some new connections with nonlinear analysis[J].SIAM Rev, 1990, 32: 537-578.

[2] Bernis F, Azorero J G,Peral I. Existence and multiplicity of nontrivial solutions in semilinear critical problems of fourth order[J].Adv Diff Eqns, 1996, 1: 219-240.

[3] Gazzola F, Grunall H C, Squassina M. Existence and nonexistence results for critical growth biharmonic elliptic equations[J].Calc Var, 2003, 18: 117-143.

[4] Bonder J,Rossi J. A fourth order elliptic equation with nonlinear boundary conditions[J].Nonlinear Anal, 2002, 49:1037-1047.

[5] Deng Y,Wang G. On inhomogeneous biharmonic equations involving critical exponents, Proc[J]. Roy Soc Edinburgh Sect A, 1999, 129(5): 925-946.

[6] Liu X,Li W. Existence and multiplicity of solutions for fourth-order boundary value problems with parameters[J].J Math Anal Appl, 2007, 327: 362-375.

[7] Lions P. The concentration-compactness principle in the calculus of variations: the limit case[J].Rev Mat Iberoamericana, 1985, 1: 45-121, 145-201.

[8] 张恭庆. 临界点原理及其应用[M]. 上海: 上海科技出版社, 1986.

Infinitely many solutions for biharmonic equation without A-R condition

XIE Huazhao

(Department of Mathematics, Henan University of Economics and Law, Zhengzhou 450056)

In this paper， we have studied the following biharmonic problem on a smooth domain Ω⊂RN(N>4):Δ2u-λu=f(x，u)，x∈Ω;u=∂u/∂n=0，x∈∂Ω，where the nonlinearityf(x，u) is odd symmetric with respect tou， has subcritical growth at infinity and does not satisfy A-R condition. Using symmetric mountain pass theorem， we prove that the above problem has infinitely many solutions， and the corresponding critical values approach to positive infinity．

biharmonic equation; infinitely many solutions; A-R condition

2014-01-10.

国家自然科学基金项目(11326136); 河南省自然科学基金项目(14B110033).

1000-1190(2014)04-0461-04

O29

A

*E-mail: hzh-xie@126.com.