Joint Optimization of Battery Allocation and Routing for Maximum Lifetime in Wireless Sensor Networks*

JIANG Zidong，FENG Hui，YANG Tao，HU Bo

(Department of Electronic Engineering，Fudan University，Shanghai 200433，China)

Joint Optimization of Battery Allocation and Routing for Maximum Lifetime in Wireless Sensor Networks*

JIANG Zidong，FENG Hui，YANG Tao，HU Bo*

(Department of Electronic Engineering，Fudan University，Shanghai 200433，China)

In order to prolong the lifetime of wireless sensor networks(WSN)，we jointly optimize the routing and battery allocation policy.The joint optimization problem is modeled with continuous and discrete battery levels respectively.In the case of continuous battery allocation，a linear programming problem is established，which obtains the optimal routing and battery allocation simultaneously.In the case of discrete battery allocation，a suboptimal but efficient method is proposed，which slacks a combinational optimization problem to a continuous form，and discretizes the battery levels in an optimal way.The simulation results show that our methods can substantially prolong the network lifetime and perform better than others.

wireless sensor networks;network lifetime;battery allocation;routing;linear programming

无线传感器网络(WSN)通常会在目标区域中放置大量的廉价传感器节点来完成数据的采集，传输与处理。由于其成本低，覆盖率高的特性，在很多领域都引起了广泛关注［1－2］，比如环境数据监测，灾难预警，目标跟踪等。在大多数的场景中，节点由电池供能，且更换电池所需要的成本很高，例如当网络布置在偏远区域中时。因此，在无线传感器网络的应用中，如何在有限的电量下延长网络的工作时间，是一项重要的工作和挑战。

无线传感器网络的寿命主要取决于节点的能耗能否平衡。在有数据汇聚节点(通常称为Sink节点)的多跳WSN中，Sink节点周围的节点由于需要转发大量数据而容易出现电量耗尽的情况，导致外部节点虽然有剩余电量，整个网络却无法继续工作。这种现象被称为能量空洞(Energy Hole)［3－5］。一些方法可以减轻这种现象，比如合理规划节点的放置策略和放置密度［6－7］，或者引入可移动的Sink节点［8－10］来平衡全网能耗。但是很多应用场景中，节点的位置是预先确定不可更改的。比如在气象数据监测网络中，节点的放置有严格的规定，这关系到测量数据的准确性。在这些场景中，节点电池电量分配［11－13］就是一个缓解能量空洞现象的有效方式。文献［11］首先提出了对节点分配不同电量的电池可以有效的延长网络寿命的观点。其多层分配方法MTA(Multiple Tiers Allocation Method)根据节点到Sink节点的跳数，将节点划分到不同的层级，同一层级采用同一种电量的电池。但是MTA的方法需要假设WSN有均匀的节点分布密度，有一定局限性，而且它的推导和分析都是基于最小跳数路由策略。文献［12－13］提出的CLPS(Cost Limited Pack Selection)没有采用“层”的结构以及均匀密度和最小跳数路由的假设，而是假设已知节点能耗分布。CLPS通过将不同电池打包为电池组，根据节点能耗分布提出了电池组分配的启发式算法。本质上，CLPS的性能还是依赖于路由，因为路由是决定节点能耗的主要因素之一，但CLPS没有对路由进行优化。

文献［14］首次提出了在已知初始电量下的最大寿命路由MLR(Maximum Lifetime Routing)，将WSN的寿命最大化问题建模成一个线性规划问题。之后，很多基于MLR的扩展和改进被提出［15－16］，但是都没有考虑到对于电量分配进行优化。可以预见到，如果电量分配和路由一起优化，网络寿命可以更长。

本文的主要贡献是将网络路由和电池电量分配进行联合优化，在连续和离散两种电池电量分配场景中分别建立优化模型并求解。仿真显示，本文的方法都可以显著地延长网络寿命，比已有方法性能更优。

1 系统模型与网络寿命

本文考虑的WSN由N个静态传感器节点和一个Sink节点组成。每个传感器节点i以固定速率采集数据，单位时间产生Si个数据。如果Si=0，节点i就只是转发数据的路由节点，否则它就是源节点，可以完成数据采集和转发的功能。如果两个节点i和j之间的距离不大于最大传输半径dmax，则它们可以直接通信，称彼此为邻居。与节点i相连的邻居集合为Ni。我们假设在所有传感器节点和Sink节点之间总存在通路，那么所有采集的数据都要通过多跳路由传输到Sink节点。数据的传输可以看成是一种网络流r∈RN×N，rij代表了节点i到j的流速率。节点i的初始电量记为Bi，并假设只有数据的发送是消耗能量的，发送单位数据到节点j消耗电量Eij。

上面提到的系统模型可以很方便的扩展到其他复杂形式［16］，包括多Sink节点网络，无Sink节点的ad-hoc网络以及考虑接收能量等，我们之后的分析和方法都将适用于这些扩展模型。

1.1 最大寿命路由

在给定网络拓扑，初始电量{Bi}和链路能耗{Eij}的情况下，MLR的目的就是设计出最优的网络流r来最大化网络寿命。文献［17］描述了不同种类的WSN寿命的定义。本文采用一种最常见的定义方式:第1个死亡节点的寿命。节点死亡等价于节点电量耗尽，所以单个节点i的寿命是

而网络寿命的定义是

基于这种寿命定义(2)，MLR可以通过求解以下的优化问题得到，

其中，q=1/Tnet。第1个约束是流约束，表示单位时间每个节点发送的数据量等于接收加采集的数据量。第3个约束确保了在Tnet时间内，没有节点耗尽电池。

(P1)是一个典型的线性规划问题［18］，它可以通过很多现有的工具包求解，比如MATLAB的CVX［19］。

2 连续电量分配场景

假设每个节点分配相同电量的电池，路由选择(P1)计算出来的MLR，那么当网络死亡时，一部分节点的电池还有剩余电量，这些电量就被浪费了。直观的理解，如果节点的初始电量被合理地分配，原本浪费的电量就能被利用，从而延长网络寿命。所以我们需要路由和电量分配的联合优化，来最大化网络寿命。接下来，我们提出了两种联合优化方法，分别针对连续电量分配场景和离散电量分配场景。本节只考虑连续电量分配场景。

连续电量分配意味着节点的初始电量可以是任意连续值。这适合于电池订做的场景，或者电池规格很多，容量间隔很小，以至于可以近似认为是连续值。考虑到制作工艺和重量的限制，最大可能的电池容量为Bmax，

假设电池价格和容量是近似线性的，那么对于价格预算约束就转化为了对于能量预算约束∑i∈NBi≤Btotal。给定网络拓扑，链路能耗的情况下，网络寿命取决于路由和节点初始电量。所以我们提出如下的联合优化问题

(P1)和(P2)的主要区别在于(P2)中，初始电量{Bi}是优化变量而不是已知值。因为存在约束的可行域不是凸集，所以它是一个非凸的优化问题。一般非凸问题的算法不能保证得到全局最优解，它的效果和初始点的选取以及迭代步长等参数有关。而接下来提出的算法要得到(P2)的最优解。

将式(4)代入(P2)，得到以下优化问题。

这里(P3)是一个凸问题(线性规划问题)，可以方便的求解。

定义(P2)的可行域为Φ2，最优值为q*。而Φ3为(P3)的可行域与对应的电量B的集合，对应关系由式(4)给出。设(P3)最优值为qc，其中一组最优解是{rc，qc}，对应的电量分配为Bc，Bc可以通过式(4)由{rc，qc}解出。这里上标c表示这些变量属于连续(continuous)电量分配的场景。

定理1{rc，qc，Bc}是(P2)的一组最优解。

证明因为式(4)是∑j∈NiEijrij≤Biq的一种特例，所以有Φ3⊆Φ2，{rc，qc，Bc}∈Φ2。为了证明定理1，只需要证明qc=q*即可。

已知{r*，q*，B*}是(P2)的一组最优解。可以得到在网络停止工作后，节点i的剩余电量为ΔBi。接下来，根据剩余电量的不同，将{r*，q*，B*}分为3种情况。

情况1:ΔBi=0，∀i∈N

这里，式(4)对每一个节点都成立，所以{r*，q*，B*}∈Φ3。因为qc是(P3)的最优值，有q*≥qc。然而，因为Φ3⊆Φ2，必然有q*≤qc。所以只能是qc=q*。

情况2:∃j∈N，ΔBj＞0以及∃i∈N，Bi=Bmax

如果在B*中去除将被剩余的部分，将得到新的分配方案Bnewi=B*i－ΔBi，∀i∈N。这样的改变不会违背(P2)的约束以及改变最优值q*。修改后的解是{r*，q*，Bnew}，它将被划分到情况1。根据之前的分析，得到qc=q*。

情况3:∃j∈N，ΔBj＞0以及∀i∈N，Bi＜Bmax

在这种情况下，总可以对电量分配做出以下调整:从浪费的电量中取出一小部分，将它平均分配到所有节点，而依旧保持∀i∈N，Bi≤Bmax。这样原来最先死亡的节点有更多的电量，在保持路由不变的情况下，网络的寿命会延长。这与q*是(P2)最优解的定义矛盾。所以这种情况是不可能出现的。

综上所述，我们得到qc=q*，从而证明了定理1。

连续电量分配与路由联合优化方法(CBAR)如下所示。由定理2可知，CBAR得到的{rc，qc，Bc}是网络寿命最大化的最优解。

算法1连续电量分配与路由联合优化方法(CBAR)

步骤1:计算路由:解线性规划问题(P3)，得到最优路由rc和对应的最大网络寿命Tnet=1/qc。

步骤2:电量分配:根据式(4)，分配各节点电量Bc。

CBAR中不存在任何的电量浪费。将式(4)代入式(1)，得到所有节点的寿命是一致的，T1=T2=…=TN=Tnet，它们将同时耗尽电量。在(P2)的多组最优解中，CBAR给出了最“节省电量”的解。

3 离散电量分配场景

在很多实际应用中，节点电池只有几种合适的规格可以选择，也就是说，节点初始电量是在一个有限集合中选择。本节考虑这种离散电量分配下的网络寿命最大化问题。

假设有K种规格的电池可供选择，按电量大小排序有bK＞…＞b1=0。所以节点的初始电量Bi满足Bi∈{b1，b2，…，bK}，∀i∈N。与(P2)类似，在给定网络拓扑和链路能耗的前提下，联合优化路由与电量分配的问题如下，

(P4)是一个组合优化问题，一般需要穷举遍历来得到最优解。如果在实际应用中，N或者K很大，采用穷举法需要很大的计算量。所以本节提出一个次优但是高效的算法。

首先，通过将离散的约束Bi∈{b1，b2，…，bK}放松为连续的线性约束Bi≤bK，得到

令Bmax=bK，利用上一节的CBAR求解(P5)，得到路由rc，连续电量分配方案Bc以及对应的最大寿命。

为了得到离散电量分配，Bc需要做离散化。定义节点i的电池序号是mi，mi∈{1，2，…，K}。由上节可知T1c=T2c=…=TcN=Tcnet。如果最终节点i的初始电池电量bmi小于连续分配的电量Bci，在路由rc不变的情况下，节点的寿命可以由式(1)推导出，

基于上式，本文提出了最优电池离散化算法(ODA)，将Bc离散化为Bd。这里上标d表示该变量属于离散(discrete)电量分配的场景。图1显示了ODA的算法流程图。图中主要过程的解释如下:

预先计算节点退化后寿命:计算当节点电池“退化”到下一个更小电量的电池时，节点的寿命，即退化后寿命

停止:得到离散电量分配方案Bd={bmi}。

图1 最优电池离散化算法(ODA)流程图

定理2经过ODA离散化后的Bd是在路由rc下最优的离散电量分配方案。

证明由ODA选择退化节点的方法，说明了节点经过退化后的寿命就是当时的网络寿命，并保证在所有可能的电池退化中，网络寿命最小限度地下降。

构造一张列表，按照网络寿命的降序，对所有可能的KN种电量分配方案进行排序。显然，最优的分配方案是第1个恰好满足能量预算约束的分配方案。由于初始松弛，初始的电量分配在列表中位于最优分配之前。步骤4导致最小的寿命减少，也就是说ODA每一次循环后，新的电量分配方案就是原来表中的下一个方案。所以ODA在循环中一定会到达最优分配并停止。得证。

尽管{Bd，rc}并不是(P4)的最优解，但是ODA给出了路由rc下的最优离散电量分配。之后通过在固定Bd下优化路由，来进一步延长网络寿命。最终，我们提出了离散电量分配与路由的联合优化方法(DBAR)，避免了穷举法的极大的计算复杂度，得到(P4)的次优解。

算法2离散电量分配与路由的联合优化方法(DBAR)

步骤1:解松弛形式:放松(P4)的离散约束，得到(P5)。利用CBAR解出Bc，rc和。

步骤2:电池离散化:在路由rc下，利用ODA将Bc离散化为Bd。

步骤3:路由改善:将Bd代入(P1)中的B，得到寿命最大路由rd以及对应的网路寿命=1/qd。

4 仿真分析

本节给出一些仿真结果，来显示联合优化的效果以及CBAR与DBAR的性能。首先利用一个水环境监测系统的例子来说明本文算法的适用场景和实际意义，之后是本文算法与已有其他算法的性能仿真与对比。

在接下来的仿真中，我们统一采用文献［20］的能耗模型来计算链路能耗，Eij=c1+c2dαij，其中设c1=1 mJ/kbit，c2=10－5mJ/kbit/m4，α=4。

4.1 水环境检测系统

考虑在水环境，比如湖泊或河流中，布置用于监测水质参数的WSN。网络中存在三类节点，源节点，路由节点和Sink节点，源节点以固定的频率采集水质数据，并借助路由节点的中继转发将此数据传递给Sink节点。在水环境中，更换节点电池是很不方便的。我们需要在有限的能量预算下尽可能延长人工维护的间隔，即网络寿命。由于存在渔业管理和航道管理，并不是水域中的任何位置都可以安放节点，节点只能存在于一些可行的位置中。此外，为了考虑监测的覆盖率和对重点区域的关注，源节点的位置可以认为是预先确定的。Sink节点的能耗不考虑，它一般与工作站相连，所以位置也是固定的。这样，在最大化网络寿命的问题中，有3种变量可以优化:路由节点的数量和位置，路由以及电量分配方案。事实上，可以忽略第1个变量，而在每一个可行的位置上都放上路由节点。在电量分配后，如果某一个路由节点分配到的电池电量是零，那就不必安置节点。这样，原问题就变成了本文之前讨论的路由和电量分配的联合优化问题。

图2显示了一种可能的网络拓扑。在边长为90 m的正方形区域中，51个节点构成了传感器网络。其中方点表示源节点，圆点表示路由节点，五角星表示Sink节点，网络中最大传输半径是20 m，源节点采集数据速率为2 kbit/s。

首先，先显示在没有电量分配的情况下，只优化路由的效果。每个节点分配相同电量的电池Bi= 100 kJ，求解(P1)得到MLR。图3(a)显示了在相同电量分配UBA(Uniform Battery Allocation)的情况下MLR的网络流。图中，边的线宽与该流的大小成正比，被标记为三角形的节点为第1批死亡的节点。当网络死亡时，除了三角形节点电量耗尽以外，其他节点都有剩余电量。图3(b)显示了这些被浪费的剩余电量，并将他们排序输出，高达总能量预算48.54%的电量被浪费了。由图3可知，虽然传统的MLR方法在确定电量分配的情况下，通过优化路由而尽可能的最大化网络寿命，但由于初始电池分配的不合理，仍然会导致当部分节点耗尽时，其他节点可能有大量剩余电量未被利用。

图2 水环境监测网络拓扑图

之后是对本文两种联合优化策略的仿真。与UBA的情况一致，能量预算为Btotal=100×50=5 ×103kJ。对于CBAR的仿真，设最大的可分配电池容量Bmax=300 kJ。图4(a)显示了CBAR的路由，图4(b)显示了对应编号节点所分配的电量。网络寿命为2.68×107s，约为310天，是UBA下寿命的两倍多。由图4可知，通过将电池分配作为优化变量，可以大幅提高最终的网络寿命，因为CBAR通过合理分配电池电量，避免了剩余电量的浪费，充分利用了能量预算，所以可以有更长的网络寿命。注意到CBAR还可以选择最终安放的路由节点的数量，比如21号节点，它在图4(a)中是孤立节点，在图4(b)中分配电池电量为零，这就表示不需要被安放。

对于离散电量分配场景的仿真，我们假设可供选择的电池电量为{0，50，100，200，300}kJ。图5 (a)显示了DBAR得到的路由和电量分配方案，节点形状代表不同电量的电池，得到的网络寿命是2.0×107s，约232 d。图中米字形的孤立节点在实际系统中不需要被放置。图5(b)显示了排序后的各节点浪费的电量。因为离散分配是连续分配的一个特例，且DBAR只是离散优化的次优算法，所以最终网络寿命比CBAR的小，且存在一定数量的能量浪费。但是与没有电量分配的UBA相比，网络寿命明显增加且能量浪费明显减少。

图3UBA仿真结果

图5DBAR仿真结果

4.2 算法对比

本节将CBAR，DBAR与UBA，CLPS和MTA(文献［14］的Problem 2)进行性能对比。为了得到更加公平和通用的结果，在每一组参数进行100个不同的随机拓扑的仿真并对结果求均值。

首先是不同的网络规模下的性能比较。五组测试场景，节点数分别是20、50、100、150和200，每组一半的节点是采集速率为2 kbit/s的源节点。能量约束随着网络规模而改变，以保证平均每个节点的电量预算是100 kJ。除此之外，区域面积也会变化，以保证5组场景下节点密度是定值0.008个/m2。我们设最大传输半径是30 m，可选择的电池电量是{0，50， 100，200，300}kJ，图5显示了不同算法的对比。注意所有的结果都与CBAR进行了归一化，因为定理1已经证明CBAR给出了最优解。CLPS的仿真选择了CBAR的路由来计算能耗分布，并且将每一种电池认为是电池组。

图6给出了以下5点事实。

(1)所有算法的性能都不如CBAR(归一化寿命均小于1)，因为在只有路由和电池分配策略可以调整的场景中，CBAR已经证明是最优策略。而仿真再一次印证了定理1的结论。

(2)尽管DBAR是一个次优方法，由于它具有最优电池离散算法，以及最后根据电池改善路由的步骤，使其效果优于已有其他方法。在所有网络规模下，DBAR均可达到CBAR的80%的性能。而CLPS的启发式电池选择方法过于保守，影响性能。

(3)在所有的网络规模下，DBAR和CLPS都比UBA的效果好，这意味着合适的电量分配对于网络寿命的延长起到重要作用。

(4)N越大，电量分配的作用(DBAR/CLPS与UBA的差距)就越明显。因为网络规模越大，UBA的能量空洞就越严重。电量分配可以很好的减轻这个现象。

(5)MTA的性能比UBA还要差。这是因为MTA的电量分配方法是基于最小跳数路由，其他算法均对路由进行了优化。此外，MTA假设节点在区域中均匀分布且有相同的采样速率，这些假设与仿真环境冲突。

之后，固定网络规模为N=50，观察电量预算约束从Btotal=2 500 kJ到Btotal=12 500 kJ变化时，各算法的性能。其他参数与之前仿真相同。图7显示了不同算法下，网络寿命与能量预算约束的关系。所有算法下，随着电量预算的增加，可以利用的总能量变多，所以网络寿命也都随之增加。各算法的性能与图6中的表现相似，在各种电量预算约束下，DBAR都优于其他离散电量分配的方法，很接近最优的CBAR。而CLPS在高预算下反而不如UBA，这显示了它启发性算法的不稳定性。

图6 不同网络规模下的性能比较

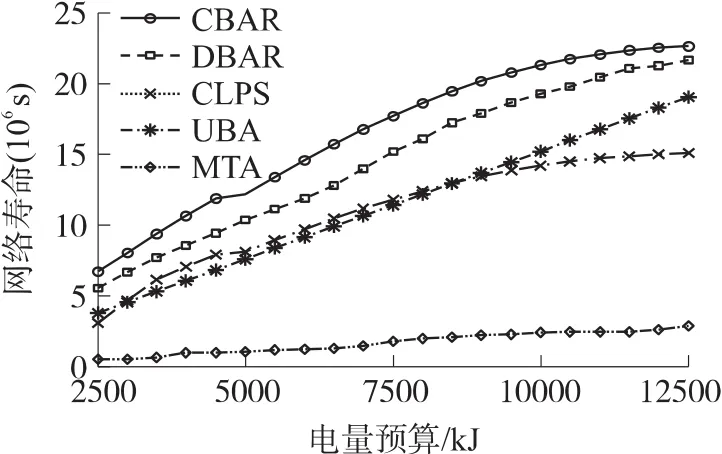
图7 不同电量预算下的性能比较

5 结论

本文通过提出在设计路由的同时，合理分配各节点电池电量，通过联合优化路由和电池电量分配，最终实现网络寿命的最大化。针对电池电量取连续值和离散值两个场景，本文分别提出了CBAR和DBAR两种联合优化算法，并有数学分析和证明。仿真结果显示，与单一优化路由或者电量分配的算法相比，本文的联合优化算法能更充分的利用能量，减小浪费，使WSN达到更长的网络寿命。

［1］Akyildiz I F，Su W，Sankarasubramaniam Y，et al.Wireless Sensor Networks:A Survey［J］.Computer Networks，2002，38(4):393－422.

［2］Chong C Y，Kumar S P.Sensor Networks:Evolution，Opportunities，and Challenges［J］.Proceedings of the IEEE，2003，91(8):1247－1256.

［3］Ahmed N，Kanhere S S，Jha S.The Holes Problem in Wireless Sensor Networks:A Survey［J］.ACM Sigmobile Mobile Computing and Communications Review，2005，9(2):4－18.

［4］刘安丰，任炬，徐娟，等.异构传感器网络能量空洞分析与避免研究［J］.软件学报，2012，23(9):2438－2448.

［5］陆海明，刘学军，钱江波.异构传感器网络的能量空洞［J］.传感技术学报，2010，23(10):1480－1485.

［6］Das D，Rehena Z，Roy S，et al.Multiple-Sink Placement Strategies in Wireless Sensor Networks［C］//Proceedings of International Conference on Communication Systems and Networks(COMSNETS)，IEEE，2013:1－7.

［7］Wang Z，Zhao X，Qian X.A Energy Balanced Deployment for Linear Wireless Sensor Networks［C］//Proceedings of International Conference on Computer Science and Network Technology(ICCSNT)，IEEE，2011，4:2345－2349.

［8］Gu Y，Ji Y，Li J，et al.EMS:Efficient Mobile Sink Scheduling in Wireless Sensor Networks［J］.Ad Hoc Networks，2013，11(5): 1556－1570.

［9］郭剑，孙力娟，许文君，等.基于移动Sink的无线传感器网络数据采集方案［J］.通信学报，2012，33(9):176－184.

［10］孙彦景，田红，王迎.多Sink协同移动的最大化网络生存期优化算法［J］.传感技术学报，2012，25(10):1433－1437.

［11］Sichitiu M L，Dutta R.Benefits of Multiple Battery Levels for the Lifetime of Large Wireless Sensor Networks［M］//Networking 2005.Networking Technologies，Services，and Protocols;Performance of Computer and Communication Networks;Mobile and Wireless Communications Systems.Springer Berlin Heidelberg，2005: 1440－1444.

［12］Long H，Liu Y，Wang Y，et al.Battery Allocation for Wireless Sensor Network Lifetime Maximization under Cost Constraints［C］// Proceedings of the International Conference on Computer-Aided Design.ACM，2009:705－712.

［13］Liu Y，Wang Y，Long H，et al.Lifetime-Aware Battery Allocation for Wireless Sensor Network under Cost Constraints［J］.IEICE Transactions on Communications，2012，95(5):1651－1660.

［14］Chang J H，Tassiulas L.Routing for Maximum System Lifetime inWireless Ad-Hoc Networks［C］//Proceedings of the Annual Allerton Conference on Communication Control and Computing.The U-niversity;1998，1999，37:1191－1200.

［15］Chang J H，Tassiulas L.Maximum Lifetime Routing in Wireless Sensor Networks［J］.IEEE/ACM Transactions on Networking (TON)，2004，12(4):609－619.

［16］Madan R，Lall S.Distributed Algorithms for Maximum Lifetime Routing in Wireless Sensor Networks［J］.IEEE Transactions on Wireless Communications，2006，5(8):2185－2193.

［17］Gandham S R，Dawande M，Prakash R，et al.Energy Efficient Schemes for Wireless Sensor Networks with Multiple Mobile Base Stations［C］//Globecom IEEE 2003，1:377－381.

［18］Boyd S P，Vandenberghe L.Convex Optimization［M］.Cambridge University Press，2004.

［19］Grant M，Boyd S，Ye Y.CVX:MATLAB Software for Disciplined Convex Programming［CP/OL］.http://cvxr.com/cvx，2009.

［20］Heinzelman W B，Chandrakasan A P，Balakrishnan H.An Application-Specific Protocol Architecture for Wireless Microsensor Networks［J］.IEEE Transactions on Wireless Communications，2002，1(4):660－670.

蒋紫东(1989－)，男，硕士研究生，研究方向为无线传感器网络，11210720022@fudan.edu.cn;

冯辉(1980－)，男，讲师，主要研究方向为无线传感器网络、分布式信号处理理论及应用;

杨涛(1970－)，男，副教授，主要研究方向为无线通信理论与信号处理;

胡波(1986－)，男，教授、博士生导师，主要研究方向为数字信号处理、数字通信，bohu@fudan.edu.cn。

最大化WSN寿命的电量分配与路由联合优化策略*

蒋紫东，冯辉，杨涛，胡波*
(复旦大学电子工程系，上海200433)

为了尽量延长无线传感器网络的工作寿命，提出了一种对网络路由和电池电量分配方案进行联合优化的策略，在连续和离散两种电池电量分配场景中分别建立优化问题模型，并给出求解算法。在连续电量分配情况下，通过转换成线性规划问题，可同时解出最优的路由和电量分配方案。在离散电量分配场景中，通过将组合优化问题松弛为连续优化问题，并提出一种最优的电池离散化算法，得到一组次优的路由和相应的离散电量分配方案。仿真显示该联合优化策略可以显著地延长网络寿命。

无线传感器网络;网络寿命;电池电量分配;路由;线性规划

TP393

A

1004－1699(2014)04－0536－08

2013－11－29修改日期:2014－04－02

C:6150P

10.3969/j.issn.1004－1699.2014.04.021

项目来源:国家教育部博士点基金项目(20120071110028)