一种叶片干摩擦阻尼器耦合振动分析的二维局部摩擦模型

何冰冰, 任兴民, 何尚文, 秦卫阳, 杨永锋, 邓旺群

(1.西北工业大学 振动工程研究所，西安 710072；2. 郑州大学 力学与工程科学学院,郑州 450001；3. 中国航空动力机械研究所，湖南 株洲 412002)

给叶片附加干摩擦阻尼器可以有效抑制航空发动机叶片振动，国内外学者已在此领域开展了大量研究。研究表明建立科学、准确的干摩擦接触模型是该类阻尼器计算、设计的关键。Iwan[1]提出了弹簧的并联和串联模型来模拟一维摩擦接触；Menq等[2-3]引入弹性剪切层模拟摩擦接触对一维局部滑移进行了研究；漆文凯等[4-5]提出了一种一维解析局部滑移摩擦模型，并在国内得到了广泛应用。随着研究深入，一维摩擦接触模型不能求解叶片阻尼器系统耦合振动问题的局限性愈加明显，且工程中叶片并非一维振动，单颖春等[6-7]利用轨迹跟踪法分析了二维运动时摩擦力的情形，其研究基于二维整体滑动模型，接触点要么滑动、要么粘滞。

实际上和一维滑动[2,8]一样，二维滑动过程中，存在着完全粘滞、局部滑动、整体滑动三种情形或阶段。本文在一维局部滑动模型[8]和二维整体滑动模型[6-7]基础上，通过带滑动触点的并联弹簧系统来模拟二维平面运动时摩擦接触点的局部滑动(部分触点滑动，部分触点粘滞)，建立了一种二维局部摩擦模型，推导了各种摩擦接触下摩擦力的计算公式，为叶片阻尼耦合振动分析打下了坚实基础。

1 二维局部滑动模型的建立

参考[8]中的一维局部滑动模型，给定相关摩擦接触参数，从临界滑动状态(接触面间将要发生整体滑动，此时摩擦力f值为μN，μ为动滑动摩擦系数，N为接触面间正压力)卸载、重复加载时干摩擦力和接触面间相对位移的迟滞曲线如图1所示。另外为了模拟接触面间一维局部滑动，Iwan[1]的弹簧并联和串联模型很有代表性，且并联模型更为直观、便捷。

图1 临界状态时摩擦力-位移迟滞曲线

用并联弹簧模型对摩擦进行模拟时，摩擦力f与位移u的关系为：

(1)

式中:序号为1到j的弹簧滑动触点已开始滑动，j+1到n的弹簧为弹性变形阶段；km与Rm分别为对应弹簧刚度及临界摩擦力。用并联弹簧模型来模拟文献[8]的一维局部模型，参考图1类椭圆内部初始加载阶段曲线，令接触面局部滑动与整体滑动的临界位移分别为u1、un，以u1为首项un为末项形成一等差数列，则第2到n-1个弹簧的临界位移为分别为数列的第2到n-1项。由初始加载曲线可得um对应的Pm，由方程(2)可解得km(m=1,2,…,n)并得到Rm。当用6个弹簧并联来模拟时如图2所示。

(2)

图2 并联模型形成迟滞曲线与图1对比

由图2可知，当弹簧个数为6时两迟滞曲线已基本重合，实质上当接触面长度、弹性模量、横截面积及滑动摩擦系数这些因素变化不大时，此结论具有较强通用性，在忽略正压力变化对接触面长度、弹性模量、滑动摩擦系数等参数的影响时对上述结论通用性影响较小。本文选用6个弹簧来模拟相同摩擦接触条件下的二维摩擦，如图4所示。令方程(2)中的n等于6进行求解，可得六个弹簧的参数km和Rm(m=1,2,…,6)。

图3中b1,…,b6为弹簧对应滑动触点，当第m个弹簧变形小于Rm/km，则bm保持粘滞状态，否则bm开始滑动，各个触点可能状态不同。

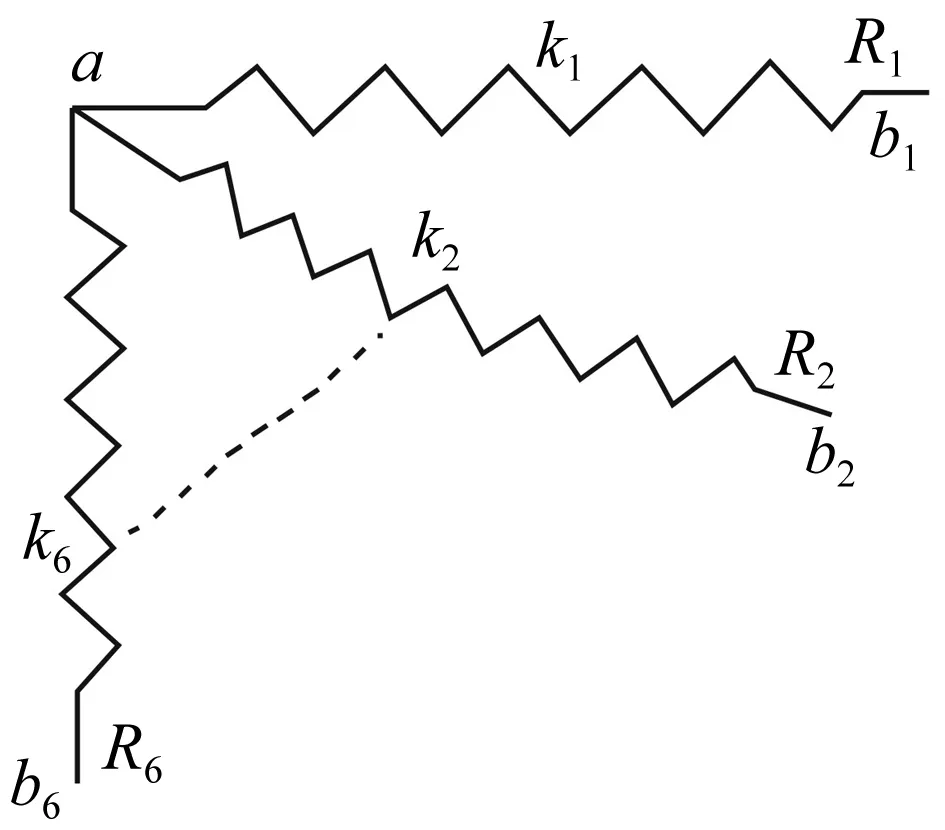
图3 二维局部滑动模型

两个接触面摩擦，a为某叶片上的摩擦触点，bm为滑动触点。设初始时bm和a重合，叶片开始振动后，由谐波平衡法[9-10]知点a轨迹为xa=Axcos(ωt+φx)，ya=Aycos(ωt+φy)，ω为外激励角频率，Ax、Ay为x,y方向振幅，φx、φy为对应初相位。已知a点的运动轨迹，由轨迹跟踪法求b1运动轨迹(其它滑动触点轨迹确定方法与b1相同)：首先将一个振动周期时间离散为适当多时刻ti(i=0,1,…,n)(n取值要兼顾精确性及计算效率)。设ti时刻a点位置ai(xai,yai)为(Axcos(ωti+φx)，Aycos(ωti+φy)),b1点位置为(xbi,ybi)。假定b1初始位置为(0, 0)，比较a0距(0, 0)的距离与R1/k1，若小于或等于，则xb0=0,yb0=0，若大于则b1将向a点运动且使摩擦力值保持R1，xb0,yb0按式(3)计算。比较a1和(xb0,yb0)间的距离和R1/k1，如果小于或等于，则b1保持不动，若大于则b1将向a点运动且使摩擦力值保持为R1，xbi,ybi(i≥1)按式(4)计算，可确定一个周期内b1的轨迹，再以这个周期最后的b1位置作为下个周期b1位置的初始点，按上述跟踪方法计算，当相邻两个周期的轨迹趋于一致时即收敛。由a点和b1点的运动轨迹可求得一个稳态周期内摩擦力大小及方向(按式(5)计算)，同理可得到其它5个弹簧所模拟的摩擦力大小和方向，将所有摩擦力分解到x和y两个方向合成可得二维接触运动时一个稳态周期内干摩擦力在x和y方向的离散数值解如式(6)所示。二维摩擦力fx、fy可通过式(7)等效为刚度和阻尼应用于叶片阻尼器系统耦合振动分析。

(3)

(4)

(5)

(6)

(7)

2 二维摩擦接触仿真及分析

一个稳态周期内，对摩擦接触面处于完全粘滞、局部滑动和完全滑动三种情况下各个滑动触点的稳态轨迹及摩擦力进行了计算。结果如图4至图8所示(各图(a)中最外曲线为触点a轨迹，图5、6、7为局部滑动的3种情形)。

图4(a)表明在一个稳态周期内各滑动触点保持粘滞(正压力很大)；图4(b)表明摩擦力均小于临界滑动摩擦力Rm(无水平直线段)，各弹簧保持弹性变形；图4(c)、4(d)说明x和y方向摩擦力和对应位移为线性关系，与一维局部滑动的规律一致，阻尼器主要显示刚度特性。

(a)完全粘滞时各个滑动触点的稳态轨迹 (b)完全粘滞时摩擦力大小随时间的变化曲线 (c)完全粘滞时x方向总摩擦力随对应位移的变化曲线 (d)完全粘滞时y方向总摩擦力随对应位移的变化曲线

(a) 部分滑动触点一直粘滞时各个滑动触点的稳态轨迹 (b) 部分滑动触点一直粘滞时摩擦力大小随时间的变化曲线 (c)部分滑动触点一直粘滞时x方向总摩擦力随对应位移的变化曲线 (d)部分滑动触点一直粘滞时y方向总摩擦力随对应位移变化曲线

由图5(a)、5(b)可知：在一个稳态周期内有4个滑动触点一直处于完全粘滞状态，对应4个弹簧保持弹性变形，模拟的摩擦力一直小于临界滑动摩擦力；2个滑动触点处于粘滑转换状态，模拟的摩擦力在振动中达到了临界滑动摩擦力(图5(b)中水平直线段)；图5(c)、5(d)说明x和y方向摩擦力和对应位移形成迟滞曲线，与一维局部模型的规律一致，均未出现整体滑动，阻尼器显示刚度及阻尼特性。

由图6(a)、6(b)可知：在一个稳态周期内所有滑动触点处于粘滑转换，所有弹簧模拟的摩擦力在振动中均达到临界滑动摩擦力(图6(b)中水平直线段)；图6(c)、6(d)说明x和y方向摩擦力和对应位移形成迟滞曲线，且x方向发生了整体滑动，y方向摩擦力和相对位移不同时达到最值；阻尼器显示刚度和阻尼特性。

(a) 所有滑动触点处于粘滑转换时各个滑动触点的稳态轨迹 (b) 所有滑动触点处于粘滑转换时摩擦力大小随时间的变化曲线 (c) 所有滑动触点处于粘滑转换时x向总摩擦力随对应位移变化曲线 (d) 所有滑动触点处于粘滑转换时y方向总摩擦力随对应位移变化的曲线

(a) 部分滑动触点保持滑动时各个滑动触点的稳态轨迹 (b) 部分滑动触点保持滑动时摩擦力大小随时间的变化曲线 (c) 部分滑动触点保持滑动时x方向总摩擦力随相应位移变化曲线 (d) 部分滑动触点保持滑动时y方向总摩擦力随对应位移变化曲线

由图7(a)、7(b)可知：在一个稳态周期内5个滑动触点处于粘滑转换状态，对应弹簧模拟的摩擦力在振动中均达到临界滑动摩擦力(图7(b)中水平直线段)，1个滑动触点一直处于滑动状态，对应摩擦力一直等于临界值(图7(b)最下水平直线)；图7(c)、7(d)与图6(c)、6(d)基本一致；阻尼器显示刚度及阻尼特性。

图8 完全滑动状态

由图8(a)、8(b)知，在一个稳态周期内所有的滑动触点一直处于滑动状态，所有弹簧模拟的摩擦力值一直等于临界滑动摩擦力，摩擦力大小变化规律与一维库伦摩擦模型相同，摩擦力方向在平面内不停变化；图8(c)、8(d)(未画出)与图7(c)、7(d)相似，x和y方向形成迟滞曲线且x方向发生整体滑动，y方向摩擦力和相对位移不同时达到最值；阻尼器显示刚度及阻尼特性。

从图4到图8接触正压力逐步减小，接触状态由完全粘滞到局部滑动再到完全滑动，在此过程中二维局部滑动模型逐步呈现出与一维局部滑动模型明显不同的一些特性(周期激振力作用下)：y方向迟滞曲线中干摩擦力与相对位移不同时达到最大或最小；一个稳态周期内二维运动可以一直保持整体滑动状态(正压力很小)。

3 结 论

(1) 二维接触运动情况下确定所有滑动触点运动轨迹时追踪一般不超过4个周期。

(2) 将局部滑动模型由一维扩展到二维，解决了一维模型不能分析叶片—干摩擦阻尼器耦合振动问题的弊端。

(3) 仿真表明二维运动与一维运动相比，接触面完全粘滞时两者的摩擦力变化规律基本一致；局部滑动时，只有前者存在摩擦力与相对位移不同时达到最值的情形；发生整体滑动时，前者存在一个稳态周期内摩擦界面间一直处于滑动状态的情形，后者不存在此情形。

[1] Iwan W D. On a class of models for the yielding behavior of continuous and composite systems[J].ASME Journal of Applied Mechanics, 1967, 89:612-617.

[2] Menq C H, Bielak J, Griffin J H. The influence of microslip on vibratory response, Part I: A new microslip model [J]. Journal of Sound and Vibration, 1986, 107(2):279-293.

[3] Menq C H, Griffin J H, Bielak J. The influence of microslip on vibratory response, Part II: A comparison with experimental results [J].Journal of Sound and Vibration, 1986, 107(2):295-307.

[4] 漆文凯,高德平.带摩擦阻尼装置系统振动响应分析法研究[J].航空动力学报，2006,21(1):167-173.

QI Wen-kai, GAO De-ping. Study of vibration response analysis method for the dry friction damping systems [J].Journal of Aerospace Power, 2006, 21(1):167-173.

[5] 漆文凯,高德平.摩擦阻尼减振设计中的局部滑动问题[J].航空学报, 2006,27(5): 805-809.

QI Wen-kai, GAO De-ping. Microslip study on friction damping and its application in design of vibration reduction [J]. Acta Aeronautica Et Astronautica, 2006, 27(5):805-809.

[6] 单颖春,朱梓根.平面接触圆运动摩擦力的解析与数值算法[J].航空动力学报，2006,17(4): 447-450.

SHAN Ying-chun, ZHU Zi-gen. Theoretical and numerical methods for solving friction force of circular motion in contact plane [J].Journal of Aerospace Power, 2006, 17(4):447-450.

[7] 单颖春,朱梓根.复杂接触运动下非线性摩擦力的求解[J].润滑与密封，2006, 175(3):73-77.

SHAN Ying-chun, ZHU Zi-gen. The solution of nonlinear friction forces when friction interfaces constrained to complex contact motions [J]. Lubrication Engineering, 2006, 175(3):73-77.

[8] 何尚文,任兴民,秦卫阳,等.基于整体-局部统一滑动模型的叶片缘板阻尼器减振特性分析[J].西北工业大学学报,2010,28(6): 872-876.

HE Shang-wen, REN Xing-min, QIN Wei-yang, et al. A method for reducing the blade vibration of platform damper using the macro-micro slip model [J]. Journal of Northwestern Polytechnical University, 2010, 28(6):872-876.

[9] Berthillier M, Dupont C, Mondal R, et al. Blade forced response analysis with friction dampers [J]. Transaction of the ASME Journal of Vibration and Acoustics, 1998,120:468-474.

[10] 闻邦椿,李以农,许培民,等. 工程非线性振动[M].北京:科学出版社, 2007：34-36.