谐波激励下多尺度粘滑干摩擦系统混沌

阎 俊，徐 超

(西北工业大学 航天学院，西安 710072)

工程结构多由螺栓、铆钉等连接装配。振动环境下连接结合面在法向可能出现间隙、分离及碰撞，在切向可能出现摩擦、滑移及滑动等非线性现象，导致连接结构发生复杂的动力学行为。对含结合面摩擦系统的研究一直为非线性动力学领域研究重点。何阿平等[1]对摩擦学行为的混沌特性进行定量研究，并实验证明摩擦学系统混沌特性。吴文健等[2]分析由干摩擦引起的粘滑振动及系统稳定性，采用数值方法获得系统经周期运动失去稳定性通用混沌路径。韩彦等[3]对干摩擦振动系统响应计算方法进行述评。陈建县[4]分别从摩擦特性、摩擦力模型、摩擦系统自激振动、强迫振动及摩擦振动控制等系统综述机械系统滑动干摩擦动力学近期研究进展，指出含摩擦系统动力学研究对工程设计、优化及控制的重要意义。

结合面干摩擦描述形式对建模系统非线性动力学特性有重要影响[5]。文献[6]对机械系统中摩擦模型进行评述，系统介绍多种常用摩擦模型，并对每种模型的构成、特点及适用范围进行较详细论述，认为动态摩擦模型能更好描述摩擦非线性行为。文献[7]对采用不同动态摩擦模型的系统非线性动力学行为进行研究，指出不同摩擦力模型的优点与不足。对一般机械结合面而言，接触压力分布不均匀，在切向振荡载荷作用下，结合面将反复经历从微观尺度滑移到宏观尺度滑动的多尺度动态摩擦过程。机械摩擦动力学研究中广泛采用的库伦摩擦模型虽形式简单，却不能准确描述多尺度物理过程[4,6]。文献[8]从结合面摩擦物理机理入手，在迟滞非线性模型[9]基础上导出描述连接面多尺度粘滑摩擦过程的参数化模型形式。文献[10]通过引入并联线性刚度项及均匀分布临界滑移力分布密度函数形式，给出改进的描述结合面多尺度粘滑过程的力学模型。

本文以典型含连接结合面振动系统为研究对象，采用滑动位移的迟滞模型[10]描述结合面多尺度粘滑摩擦过程，利用中心差分法，数值研究系统受谐波强迫激励时在主共振、次共振条件下的混沌特性。

1 含结合面多尺度粘滑摩擦系统模型

机械结构中典型的螺栓连接见图1。两被连接件通过施加预紧载荷螺栓装配在一起。通常预紧力在结合面上产生的接触压力p分布并非均匀，靠近螺栓孔中心区域的接触压力高，离中心越远接触压力越低。

图1 切向力作用螺栓连接结构

受切向载荷作用时，接触压力较低区域先发生滑动，而接触压力较高区域仍保持粘滞，从而接触界面处于既存在局部滑移亦存在局部粘滞状态；若切向载荷足够大，则整个结合面处处均会发生滑动，即形成动态相对运动。局部滑移可能发生于10-6～10-4m尺度，而宏观滑动则可能发生在10-3～10-2m尺度；因此，结合面动态摩擦过程具有典型的多尺度特征。

考虑图1谐波激励下典型的螺栓连接系统，因对称性且只考虑沿结合面的切向运动，可简化为图2(a)的运动模型。模型中下连件固定，上连件考虑为一维运动刚体。u，f，fesin(ωt)分别为结合面相对位移、非线性迟滞恢复力及谐波外激励力。连接系统刚度包括并联两部分，即由结合面粘滑摩擦行为的贡献及因连接件柔性的贡献。前者随结合面相对位移增大而减小呈非线性变化，后者视作线性刚度。令k表示系统初始总刚度，与结合面粘滑摩擦行为无关的线性刚度为ka=k，无量纲系数0<α<1；则描述结合面粘滑摩擦部分的子系统初始刚度为k-ka。

图2 Iwan摩擦振子及Iwan模型

力学模型实际为并联的线性刚度项Iwan模型[10]，见图2(b)，其采用n个弹簧滑块单元并联组成的子系统(经典Iwan模型)描述结合面多尺度粘滑摩擦行为。子系统中每个线性弹簧刚度ki(i=1,2,…n)均为(k-ka)/n，但每个滑块的临界滑移力fi(i=1,2,…n)不相同。系统切向受载时，临界滑移力小的滑块先发生滑动，随相对位移增大，发生滑移滑块越多，直至全部滑移，即结合面出现宏观相对运动；因此，该模型可较好复现结合面上复杂的多尺度粘滑摩擦过程。

考虑经典Iwan模型连续形式，取n→∞，则fi需定义成分布密度函数Φ(fi)形式(表达式非唯一)。定义Φ(fi)为均匀分布形式[11]，即

(1)

式中：fy为结合面恰发生宏观滑移时对应的临界宏观滑移力。

经典Iwan模型恢复力骨干(backbone)曲线fo可表示为未发生滑移的弹簧滑块单元与发生滑移的弹簧滑块单元上恢复力之和,即

(2)

将式(1)代入式(2)积分并整理得：

fo[k(1-α),u]=

(3)

式(3)分段函数包括两部分，分别表示结合面处于局部滑移与宏观滑动状态时恢复力-变形关系。振荡载荷下结合面会出现反复的卸载-加载运动。据梅辛准则[8],得迟滞过程中Iwan模型恢复力函数为

(4)

式中：fl，fu分别为卸载、加载中恢复力；A为系统一个振动周期内最大振幅。

引入无量纲参数g=f/fy,q=ku/fy,Q=kA/fy对式(2)、(4)正则化得：

(5)

(6)

据牛顿第二运动定律，图2(a)系统运动方程可表示为

(7)

对式(7)正则化，两边同乘k/(mfy)得：

(8)

(9)

2 计算方法

式(9)振动系统迟滞恢复力具有变刚度、变阻尼非光滑、强非线性特点，公式解析解较难获得。本文用中心差分法求解运动方程，研究多尺度粘滑摩擦系统随外激励幅值逐渐增大表现出的分岔及混沌特征。

由于恢复力分段及迟滞特性，数值仿真中准确判断转折点至关重要。

2.1 局部滑移与宏观滑移转折点

由式(5)知，该转折点对应的结合面相对位移为

(10)

当结合面相对位移超过qmax时，则判断系统进入宏观滑移状态，恢复力用式(5)第2式计算。

2.2 迟滞回线卸-加载转折点

迟滞回线中卸-加载转折点即系统相对速度为零时刻，判断式为

(11)

即当i与i+1时刻速度符号相反、两者乘积满足小于等于零，且要求i+1时刻速度不等于零时，则i时刻为卸-加载转折点。由于数值仿真中采用固定步长，式(11)判断的转折点仅为近似转折点，但系统分析步长足够小时，近似误差亦小。

(12)

当ε=0时，式(12)线性系统称为式(7)的派生系统，其中ωo为派生系统固有频率，ω为外激励频率。ωo接近外激励频率ω时(ωo≈ω)，系统存在主共振现象；ωo接近外激励频率ω的1/2时(2ωo≈ω)，系统发生强烈1/2次亚谐波共振现象。引入比值变量Ω=ω/ωo，取Ω=1，Ω=2分别研究系统主共振及1/2亚谐波共振下混沌形态。每类情况下分别选α=0(不考虑线性刚度项)与α=0.5两种，对比分析发生宏观滑移后系统剩余刚度对混沌形态影响。

令时间τ为第三维，将式(9)平面非自治非线性系统扩维成三维，得系统庞加莱截面为

(13)

建立τ=0时初值点及其按解的路径经时间2π/Ω后所达点间之关系。即主共振与1/2亚谐共振下系统平衡点附近的庞加莱映射。进一步将系统离散成庞加莱点映射系统为

gi+1=y(gi)

(14)

(15)

3 结果与讨论

3.1 1∶1共振

α=0时，图3(a)～(d)给出典型参数值下系统庞加莱截面。全局分岔见图7(a)。由图3可知，ge在零点附近激励幅值量级较小不足以使滑块单元产生滑动，系统非线性不明显。在微小扰动下仅存在s+，s-两段实时变化的互异双曲型平衡曲线(图3(a) 庞加莱映射)反对称落在q=0轴两边；ge继续增大，庞加莱截面上两曲线段在ge=2处螺旋式趋于各自与之同侧的互异双曲平衡点s+，s-(图3(b)庞加莱映射)，此处两平衡点稳定流形Ws(s+)，Ws(s-)与不稳定流形Wu(s+)，Wu(s-) 满足：Ws(s+)∩Wu(s-)≠0，或Ws(s-)∩Wu(s+)≠0，即重合后形成不变流形，由此断定ge=2为异宿点；异宿轨道上点当τ→+∞及τ→-∞时分别趋近于各自不同的s+，s-。上述流形稳定性判别可据Peixoto[12]定理；由于该系统不同双曲鞍点s+，s-的稳定流形Ws(s+)，不稳定流形Wu(s-)横截相交于ge=2点，则该点亦称为横截异宿点，可通过Melnikov[13]方法判定。ge逐渐增大到2.07，庞加莱截面上平衡点(周期解)个数突增至6个，图7(a)拓扑分支与图3(c)说明经叉式分岔打破原稳定平衡解。ge=2.5时，系统由P6周期轨道过渡到混沌带，图3(d)～(f)分别为该点的庞加莱映射、功率谱、吸引子；之后系统重复经历P2→混沌过程；可见，系统伴随刚度减小及弹塑性过程的不断交替，最终出现混沌运动原因为横截异宿点的产生，此时双曲鞍点稳定流形与不稳定流形为不同吸引子的吸引域边界，与不稳定流形横截相交后变为极复杂从而成为分形边界，使运动具有极端敏感性。

图3 庞加莱截面、功率谱及吸引子

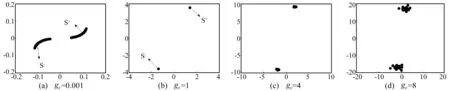
图4 庞加莱截面

α= 0.5时，与α=0对比发现，最初小扰动下系统仍存在s+，s-两个实时变化的互异双曲型平衡曲线段见图4(a)，反对称落在q=0轴两边，较α=0早于ge=1处开始螺旋式趋于与之同侧的互异双曲平衡点s+，s-，见图4(b)。同理可验证ge=1为异宿点，但异宿轨道上点τ→-∞时，趋近于s+，s-；而τ→+∞时，轨线上点不再趋近于s+，s-，而发散开形成多倍周期Pn轨道，庞加莱截面上呈现多个离散点见图4(c)～(d)；由此判断ge=1非横截异宿点。全局分岔见图7(b)，系统始终未出现混沌轨道；因此，线性刚度项对系统动力学行为影响至关重要。

3.2 1∶2共振

α= 0时，微小扰动下零点附近存在s1，s2不变流形双曲平衡点见图5(a)。ge渐增至0.5，图5(b)为两个双曲平衡点融合为s过程。此处稳定流形Ws(s)与不稳定流形Wu(s)满足相交条件Ws(s) ∩Wu(s) ≠ 0直到ge≈0.8附近，螺旋式趋于完全融合的双曲平衡点s，则上述集合中同宿点在ge≈0.8附近，此时对应的Ws(s)与Wu(s)彼此重合。同宿轨道上点τ→±∞时均趋近于一点s。

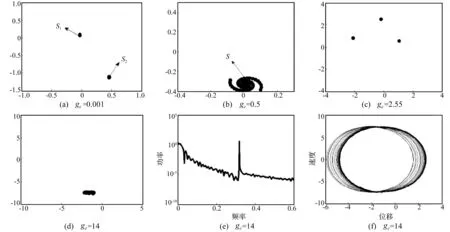
图5 庞加莱截面、功率谱及吸引子

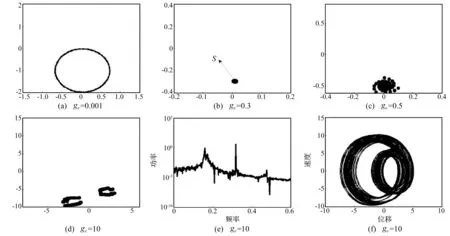
图6 庞加莱截面、功率谱及吸引子

图7(c)为区间[0,2]上分岔图。该区间同宿分支点不止一个；因此推断[13]，若存在同宿点s∈Ws(s) ∩Wu(s)，则s同时在Ws(s)，Wu(s)上。由于Ws(s)，Wu(s)均为不变流形，故对整数m,gm(s)也在Ws(s)，Wu(s)上，gm(s)为同宿点，必有无穷多同宿点存在，由此证明ge∈[0, 2]区间上不止一个同宿点，使该区间上不变流形异常复杂。ge=2.55时，庞加莱截面上平衡点个数突增至3个，系统经局部叉式分岔改变其拓扑结构，打破原稳定平衡态，变化过程见图5(c)；之后循环出现3次叉式分岔，分别为ge=3.9处P3→P1，ge=4.1处P1→P3，ge=4.5处P3→P1。ge相对较大时系统出现柱状混沌域。图5(d)～(f)分别为ge=14时的庞加莱映射、功率谱及奇异吸引子。

α= 0.5时，与α= 0 对比发现，初始阶段小扰动下庞加莱截面显示准周期运动轨道见图6(a)，ge=0.3处转换为图6(b)的稳定周期运动s，其稳定流形Ws(s)与不稳定流形Wu(s)彼此重合。同理ge=0.3点为同宿分岔点，s轨为同宿分岔轨道。同宿轨道上点τ→ ±∞时均趋近于s轨。图7(d)说明在区间ge∈[0, 16]上不止出现一个ge=0.3的同宿分岔点。图6(c)ge=0.5也为同宿点，说明α= 0中必存在无穷个同宿点使不变流形复杂程度提高，最终出现内嵌式混沌轨道。可通过图6(d)～(f)在ge=10处的庞加莱映射、功率谱、奇异吸引子说明混沌现象。

图7 全局分岔图

4 结 论

以往简单的干摩擦库伦模型振子大多验证通过周期倍化分岔、Hopf分岔及周期运动失稳等常见路径通向混沌。本文在干摩擦振子基础上，通过对多尺度粘滑摩擦振子混沌分析，结论如下：

(1) 考虑结合面的多尺度粘滑干摩擦情况存在的异宿、同宿分岔系统运动具有极端敏感性，小扰动下即可能出现混沌，从而验证同宿、异宿轨道通向混沌的路径，并表明庞加莱映射的双曲鞍点稳定流形与不稳定流形是否相交与混沌运动是否发生密切相关。

(2) 系统在1∶1共振下因存在横截异宿点，双曲鞍点稳定流形、不稳定流形为不同吸引子的吸引域边界，与不稳定流形横截相交使系统拓扑结构异常复杂成为分形边界，使运动具有极端敏感性，出现混沌。

(3) 系统1∶2共振下因存在无穷个同宿分支点，使不变流形异常复杂，系统受小扰动时，可能出现混沌运动。

[1] 朱华, 葛世荣.摩擦学系统的混沌特征[J].机械工程学报, 2004, 40(12):10-13.

ZHU Hua, GE Shi-rong.Chaotic characteristics of tribological systems[J].Chinese Journal of Mechanical Engineering, 2004, 40(12):10-13.

[2] 丁旺才, 张有强, 张庆爽.含干摩擦振动系统的非线性动力学分析[J].工程力学, 2008, 25(10):212-217.

DING Wang-cai, ZHANG You-qiang, ZHANG Qing-shuang.Nonlinear dynamics analysis of vibrate system with dry friction[J].EngineeringMechanics, 2008, 25(10):212-217.

[3] 白鸿柏, 黄协清.干摩擦振动系统响应计算方法研究综述[J].力学进展, 2001, 34(4):527-534.

BAI Hong-bai, HUANG Xie-qing.An overview on study of methods of response computation for the dry frictionally damped vibration systems[J].Advances in Mechanics, 2001, 34(4):527-534.

[4] 丁千, 翟红梅.机械系统摩擦动力学研究进展[J].力学进展, 2013, 43(1):112-131.

DING Qian, ZHAI Hong-mei.The advance in researches of friction dynamics in mechanics system[J].Advances in Mechanics, 2013, 43(1):112-131.

[5] 蔡力钢，王锋，李玲.栓接结合部动态特性研究进展[J].机械工程学报, 2013, 49(9): 158-168.

CAI Li-gang, WANG Feng, LI Ling.Review on dynamic properties of bolted joints[J].Chinese Journal of Mechanical Engineering, 2013, 49(9): 158-168.

[6] 刘丽兰, 刘宏昭, 吴子英,等.机械系统中摩擦模型的研究进展[J].力学进展, 2008, 38(2):201-213.

LIU Li-lan, LIU Hong-zhao, WU Zi-ying,et al.An overview of friction models in mechanical systems[J].Advances in Mechanics, 2008, 38(2):201-213.

[7]Awrejcewicz J, Olejnik P.Analysis of dynamic systems with various friction laws[J].Applied Mechanics Reviews, 2005, 58:389-410.

[8] Segalman D J.Modeling joint friction in structural dynamics[J].Structural Control & Health Monitoring, 2006, 13(1): 430-453.

[9] Iwan W D.Thedynamic response of the 1-DOF bilinear hysteretic system[J].In: Proc.3rd World Conf.Earthquake Eng., New Zealand: University of Auckland, 1965, 2: 783- 796.

[10] Song Y.Modeling, identification and simulation of dynamics of structures with joints and interfaces[D].Urbana, Illinois: University of Illinois, 2004.

[11] Iwan, W D.Adistributed-element model for hysteresis and its steady-state dynamics systems[J].ASME Journal of Applied Mechanics, 1966, 33:893-900.

[12] Peixoto M C, Peixoto M M.Structural stability in the plane with enlarged boundary conditions[J].Acad., Brazil.Sci., 1959, 31:135-160.

[13] 杨绍普, 申永军.滞后非线性系统的分岔与奇异性[M].北京: 科学出版社,2003.