正交异性钢桥面板疲劳裂纹扩展机理及数值模拟研究
朱劲松,郭耀华
(1.天津大学 建筑工程学院,天津 300072;2.天津大学 滨海土木工程与安全教育部重点实验室,天津 300072)
随公路桥梁向跨径大、车道多、轻柔方向发展,混凝土桥梁不再满足实际交通发展需求。由相互垂直的纵肋、横梁和及桥面板焊接而成的正交异性钢桥板,凭借承载能力大、自重轻、施工快、结构美观等优点可较好解决桥梁自重、承重、跨径间矛盾,已成为大跨径钢桥的首选桥面形式。然而由于正交异性钢桥面板不仅直接承受车轮荷载的反复作用,且作为主梁的一部分共同参与受力,从而造成局部承受应力循环次数过多,加之焊接缺陷、应力集中影响,使钢桥面板极易产生疲劳裂纹[1-2]。如英国Seven桥建成5年后即产生多种疲劳裂纹。日、美、德等国亦在正交异性钢桥面板桥梁上发现疲劳裂纹[3]。我国钢桥设计、建设起步较晚,虽汲取国外钢桥疲劳设计的宝贵经验及研究成果,但由于公路交通流量大、载重超载等实际情况及缺乏符合我国情的设计规范约束,部分钢桥均出现疲劳裂纹,如虎门大桥、江阴长江公路大桥等。大跨度钢桥一旦出现疲劳裂纹,不仅维修困难、费用昂贵,且会引起桥梁突然破坏的灾难性事故,如美国的Point Pleasant 桥断裂事故。目前疲劳开裂导致维修加固需求十分突出,而维修加固方法并非有效,原因为对疲劳失效机理研究不深入。
本文通过分析正交异性钢桥面板疲劳损伤累积并由其引发的裂纹扩展机理,采用有限元方法模拟疲劳裂纹扩展,计算中通过对疲劳细节处应力幅修正,考虑车辆轮轴横向位置、平均日交通量、年增长率和及冲击系数等因素影响,获得等效应力幅。其中冲击系数用车桥耦合振动模拟程序对全桥模型进行加载获得。对某钢桥典型疲劳细节进行疲劳裂纹扩展数值模拟,并与实桥检测结果进行对比分析表明,本文方法与计算流程可行、准确,并为通用的正交异性板钢桥抗疲劳设计及开裂加固提供理论指导。
1 正交异性钢桥面板细节疲劳开裂
1.1 正交异性钢桥面板疲劳细节类型
正交异性钢桥面板为全焊接结构。由于焊接部位的疲劳强度通常较非焊接部位低得多,且焊接部位存在焊接缺陷及应力集中,导致纵肋、横梁、桥面板交叉的应力敏感部位极易产生疲劳裂纹。结合国内外正交异性钢桥面板疲劳裂纹调查结果[4],正交异性钢桥面板典型疲劳细节分类见表1。

表1 正交异性钢桥面板典型疲劳裂纹分类
1.2 疲劳损伤-断裂失效机理分析
据正交异性钢桥面板疲劳裂纹成因不同,可分为由主应力引起的裂纹与由次应力引起的裂纹。前者称荷载引起的裂纹,后者称面外变形引起的裂纹。导致疲劳敏感部位应力幅过大原因又分为内因、外因,内因为疲劳细节自身缺陷,如焊接缺陷及安装误差等;外因为汽车活载循环往复作用等[5]。在内外因共同作用下,细节部位疲劳累积损伤一旦达临界值则发生损伤成核、产生宏观裂纹,宏观裂纹按断裂力学裂纹扩展机理扩展直至发生脆性失效断裂。
2 疲劳裂纹扩展数值模拟方法
大跨度桥梁体积庞大、结构复杂,进行全桥精细化有限元分析工作量巨大,实际计算中较难实现。本文进行疲劳细节部位应力幅计算时,采用局部精细化有限元模型;确定各疲劳细节部位冲击系数时用梁单元建立全桥有限元模型进行分析;对应力幅进行等效计算时,综合考虑车辆轮轴横向位置分布、平均日交通量、年增长率及冲击系数对钢桥疲劳细节部位应力幅影响,修正获得等效应力幅值;对各疲劳细节建立子结构有限元模型,利用应力等效原则求得所需施加的荷载值进行疲劳裂纹扩展数值模拟。
2.1 等效应力幅
2.1.1 疲劳荷载模型
我国现有公路桥梁设计规范中尚无关于汽车疲劳荷载的明确规定。文献[6-7]则规定疲劳车总重分别为320 kN及325 kN;朱劲松等[8]通过对重庆朝天门大桥、苏通长江大桥、湛江海湾大桥等设计交通流量及不同车型所占比例进行统计分析提出的标准疲劳车总重约为320 kN。故对我国公路桥梁进行疲劳分析时也可据文献[6-7]选取。本文采用BS5400标准疲劳车计算分析,该标准疲劳车轴重布置见图1。

图1 BS5400标准疲劳车轴重布置图(单位mm)
随交通量激增及汽车超载严重,致部分道路及桥梁在使用初期即出现破坏,故进行钢桥疲劳分析时,车辆超载影响不可忽略,其影响可通过调查确定超载系数考虑。
2.1.2 车辆轮轴横向分布
正交异性钢桥面板疲劳细节部位应力幅对车辆荷载位置较敏感,而车辆在行驶过程中的横向位置具有随机性,故在进行疲劳分析过程中需考虑车辆轮轴位置横向分布等效损伤影响。国外规范[9-11]均有关于车辆轮轴位置横向分布的概率模型,与吴冲等[12]调查虎门大桥提出的概率模型对比发现,国内车辆轮轴位置的分散程度远大于国外。为与国内车辆实际通行状况相符,本文采取此车辆轮轴位置横向分布概率模型。据不同加载工况各疲劳细节应力影响线及所用车辆轮轴位置横向分布概率模型,按Miner线性累积损伤法获得第j轴引起的等效应力幅值为
(1)
式中:Δσj·eq为车辆第j轴引起的等效应力幅;pi为第i种车辆轮轴横向位置频率;Δσi为第i种车辆轮轴横向位置对应的疲劳细节部位应力幅;m为应力幅-寿命曲线斜率参数,一般取3。
2.1.3 平均日交通量
桥梁平均日交通量的大小将直接影响桥梁设计使用寿命期限内桥梁遭受的疲劳循环荷载次数,从而影响桥梁疲劳寿命及疲劳裂纹扩展进程。桥梁设计使用寿命期内,能引起构件疲劳损伤的荷载循环次数NV计算式为
NV=365T∑(RiωiAAADT)
(2)
式中:T为桥梁设计使用寿命(年);AAADT为桥梁年平均日交通量;Ri为模型车辆荷载频谱值中第i辆车车轴数;ωi为第i辆模型车日交通量占年平均日总交通量比例。
2.1.4 交通量年增长率
一般通过交通量年增长率α考虑交通量增长率对NV的影响[13]:
(3)
对考虑平均日交通量及年增长率的变幅应力幅等效处理
(4)
式中:nj为车辆第j个轴所致应力循环次数;Δσj为车辆第j个轴所致应力幅值。
2.1.5 冲击系数
汽车以一定速度驶过桥梁时,由于桥面不平整、发动机振动等因素会使桥梁发生振动,从而造成内力增大,此动力效应称为冲击作用,一般通过冲击系数μ考虑[14]。本文采用车桥耦合振动模拟程序对实桥模型进行分析[15],以获取各疲劳细节部位的冲击系数,研究冲击系数对疲劳裂纹扩展影响。考虑车辆轮轴横向位置分布、平均日交通量、年增长率及冲击系数对钢桥疲劳细节部位应力幅影响,修正得等效应力幅值Δσeq为
2.2 疲劳裂纹扩展过程模拟
2.2.1 疲劳裂纹扩展路径
本文采用能量释放率准则对二维疲劳裂纹扩展路径进行数值模拟。能量释放率为裂纹边缘扩展单位面积释放处能量,能量释放率理论亦称G准则,其两假设[16]为
(1) 裂纹沿应变能释放率最大方向开始扩展;
(2) 能量释放率达到一定临界限值时,裂纹开始扩展,得能量释放率断裂准则:
(6)
式中:Gθ为裂纹扩展能量释放率;v为裂纹相对位移;E为材料弹性模量;θ0为裂纹扩展方向角;KIC为材料断裂韧度。
2.2.2 疲劳裂纹扩展寿命
通常结构焊接部位存在焊接缺陷及应力集中,疲劳裂纹易产生于此处,裂纹稳定扩展阶段可决定结构的疲劳寿命,Paris等[17]基于线弹性断裂力学提出的裂纹扩展速率公式为
da/dN=C(ΔK)m
(7)
式中:a为裂纹深度;N为应力循环次数;C,m为材料常数[18],取C=6.89×10-12,m=3;ΔK为应力强度因子幅值,可通过有限单元法计算[19-20]。
裂纹扩展速率直接决定裂纹扩展寿命及钢桥构件的疲劳寿命,对式(7)积分得钢桥疲劳裂纹扩展寿命计算公式为
(8)
式中:a0为裂纹初始深度,取0.1 mm;ac为裂纹最终扩展深度,对顶板及纵肋取板厚[21],为方便对比横隔板也取顶板厚度。
2.2.2 疲劳裂纹扩展数值模拟流程
在以上分析基础上提出的正交异性钢桥面板疲劳裂纹扩展数值模拟方法流程见图2。

图2 疲劳裂纹扩展数值模拟流程图
3 实例分析
3.1 实例概况
天津滨海新区某公路大桥为独塔斜拉桥,主桥全长500 m,主梁为钢混结构,主跨除近主塔附近20 m为预应力混凝土箱梁外,其余290 m为正交异性钢桥面板钢箱梁,钢箱梁桥面铺装7 cm厚沥青混凝土。通车8年后对该桥检测时,在主跨钢梁中发现大量疲劳裂纹。为给此类桥梁抗疲劳设计、裂纹检测周期确定提供理论依据,采用本文方法对该桥典型疲劳裂纹扩展过程进行数值分析。
3.2 有限元模型
利用ANSYS有限元软件建立全桥三维有限元模型见图3,拉索采用Link8单元,主塔、正交异性钢桥面板主梁及混凝土主梁均采用Beam188单元。选主跨跨中主梁截面各疲劳细节进行细部分析,利用车桥耦合振动程序对全桥进行分析,获得各疲劳细节部位的应力冲击系数。建立钢桥面板局部有限元模型,桥面采用空间板桥单元Shell63,桥面铺装采用Solid45单元。由于各疲劳细节部位应力影响线较短,为使一辆标准疲劳车能全程通过,考虑边界条件影响,计算模型纵向取10个标准阶段(3.2 m),纵向长度32 m,横向宽度6个纵肋宽度计3.6 m,顶板、横隔板、纵肋厚度分别为14 mm、10 mm、6 mm,并计及7 cm桥面铺装。模型全局采用0.1 m网格密度,疲劳细节部位采用0.02 m网格加密。局部模型两端采用简支约束,并在横梁两端加横、竖向位移约束及绕纵轴、竖轴转动约束,限制横梁底端的竖向位移,模型见图4。
图3 斜拉桥有限元模型

图4 桥面板有限元模型
3.3 等效疲劳应力幅
该桥为双向四车道,单车道通行量15 000辆/天,采用BS 5400疲劳标准车对桥面板进行加载。为考虑车辆轮轴横向位置对疲劳细节处影响,需将疲劳标准车在横向分别置于不同位置加载分析,由于BS 5400疲劳标准车单个轮胎触地面积为0.2 m×0.2 m,因此可取横桥向每偏离0.2 m作为一加载工况,据车辆轮轴位置横向分布概率模型,车轴偏离中心位置大于0.8 m的概率几乎为零。综上所述,分9个加载工况,见图5。
多座正交异性钢桥面板钢桥病害检测结果表明,疲劳裂纹产生最多部位为U肋与横肋交叉处(A类)及U肋与桥面板焊接连接处(B类),其中产生于U肋与顶板焊根处的焊缝开裂裂纹A2可通过提高焊接质量避免,因此选取A1,B1,B2三类疲劳裂纹建模、分析,并以A1疲劳细节为例,说明等效应力幅计算方法。由于BS 5400疲劳标准车4个轴重相同,且前两轴与后两轴相距较远,影响线间相互影响较小,为显示方便仅列出前两轴应力历程,不同工况下A1疲劳细节应力历程见图6。
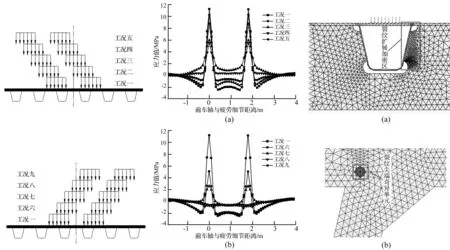
图5 加载工况

3.4 疲劳裂纹扩展
钢桥焊缝处最易发生疲劳裂纹。由于整体模型受单元尺寸限制无法体现焊缝细节部位的应力情况,需对受损局部区域建立子模型模拟此处裂纹扩展。按本文方法对A1疲劳细节建模,局部子模型采用Plain82单元,在裂纹尖端区域采用奇异单元精细划分,并对裂纹扩展区域加密处理,模型两端采用简支约束,并对底端加竖向约束;基于应力等效原则,将等效应力幅转化为施加于桥面板的荷载,疲劳细节部位有限元模型见图7。
3.4.1 扩展路径
对A1疲劳裂纹,当纵肋内侧弯矩大于外侧时,裂纹产生在焊趾处,反之则产生在焊根处。A1,B1,B2处疲劳裂纹扩展数值模拟结果与实桥检测裂纹模式对比见图8、图9。由二图看出,用本文数值模拟方法所得裂纹扩展路径与钢桥实际疲劳裂纹扩展路径相近,证明此方法准确、可行。
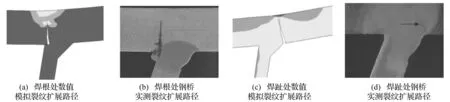
图8 A1处疲劳裂纹扩展路径对比

图9 B1、B2处疲劳裂纹扩展路径对比
3.4.2 扩展寿命
对A1焊根、焊趾处及B1,B2处疲劳裂纹进行裂纹扩展寿命分析,结果见图10。由图10可见,初期裂纹扩展较慢,深度超3 mm后迅速扩展。对比4种裂纹类型,B1与B2处裂纹疲劳寿命较短,此因横隔板限制U肋的挠曲变形,连接焊缝处应力较大,且横隔板面内变形及应力在开口处U肋变形处发生较大应力集中[22];A1处疲劳裂纹尖端承受应力幅值较小,故其疲劳寿命相对较长。
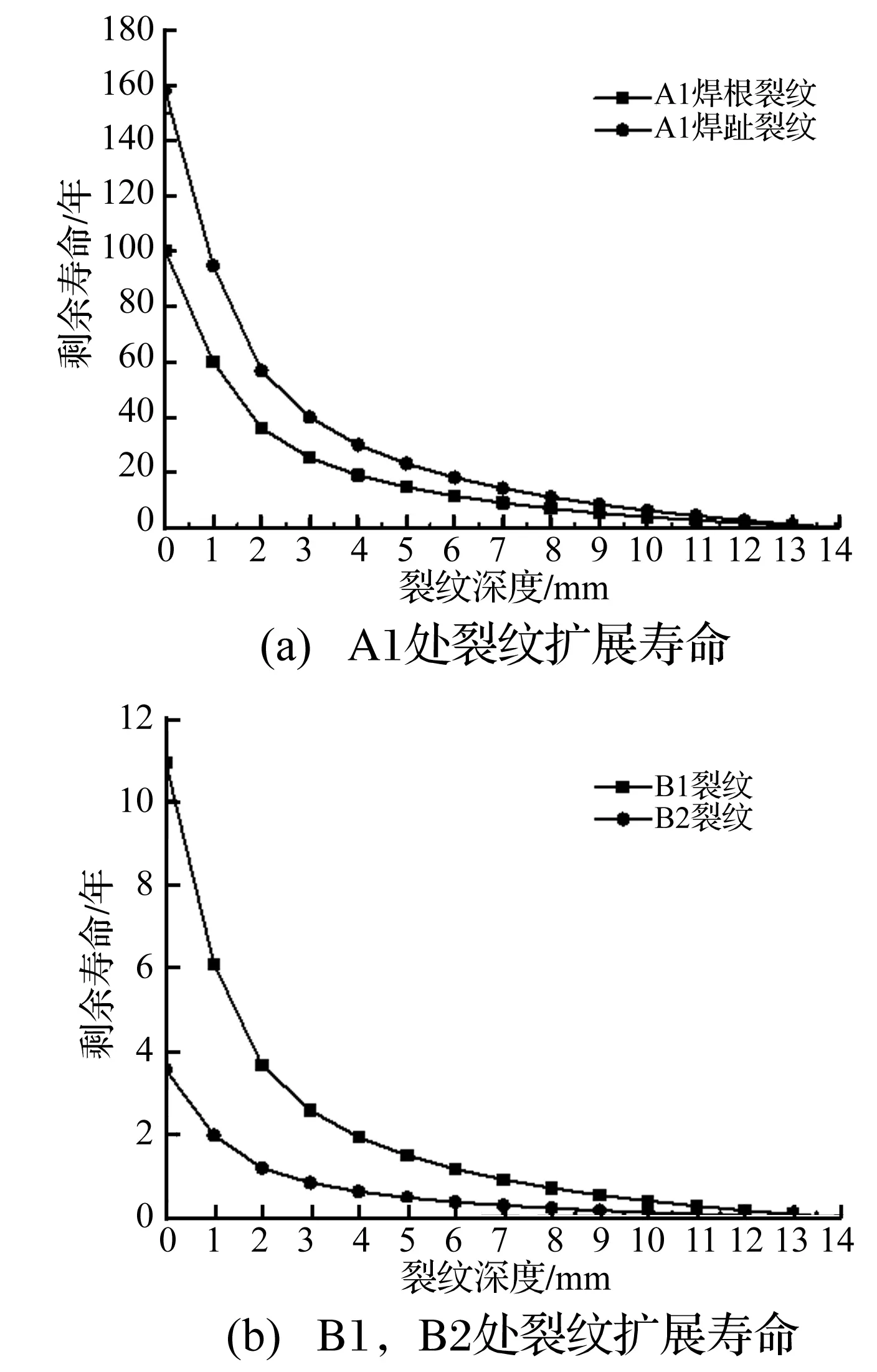
图10 疲劳裂纹扩展寿命
3.5 参数影响
3.5.1 铺装厚度
进行钢桥面疲劳分析时铺装层作用不可忽略[23]。选铺装层弹性模量3400 MPa、分析铺装层厚度5 cm,7 cm,9 cm,11cm时,钢桥各疲劳细节部位裂纹扩展寿命结果见图11。由图11可见,A1焊趾处疲劳裂纹扩展初期,铺装层厚度由7 cm增至9 cm,其剩余寿命延长约38%;铺装层厚度由7 cm减至5 cm,其剩余寿命则缩短约30%。其余细节处疲劳裂纹变化趋势类似,说明疲劳裂纹扩展寿命对铺装层厚度变化较敏感,此因铺装层厚度的增加可直接降低各疲劳细节处疲劳应力幅值,延长其裂纹扩展寿命。
3.5.2 路况
桥上路面粗糙程度分为很好、好、一般、差及很差5个等级[15]。各路况下疲劳细节处冲击系数不同,会直接影响到裂纹扩展寿命,因此需考虑桥上路面粗糙度对各疲劳细节裂纹扩展寿命影响。选BS 5400疲劳标准车,车速60 km/h、桥面铺装层厚7 cm进行分析,结果见图12。由图12看出,各疲劳细节处裂纹扩展寿命随路况的变差而缩短,其中以路况一般为分界线,当路况退化到一般以下后,裂纹扩展寿命迅速缩短。此因路面较粗糙时车辆行驶不平稳,跳车现象严重,导致车辆对桥梁冲击力增大,疲劳细节部位所受应力幅值增大,从而致使裂纹扩展寿命降低。
3.5.3 超载
我国车辆超载现象非常严重,从而加速路面破坏,缩短检修期,使养护费用成倍增加。为研究超载对钢桥疲劳裂纹扩展寿命影响,分析车速60 km/h,路面粗糙度为一般、桥面铺装厚7 cm时,车辆超载系数分别为1.0、1.2、1.4、1.6、1.8、2.0六种工况下疲劳裂纹扩展寿命,结果见图13。由图13看出,随车辆超载量的增加,各疲劳细节处裂纹扩展寿命急剧缩短,超载量60%时,各疲劳细节处裂纹扩展寿命已缩短至无超载时的一半。
3.5.4 交通量年增长率
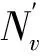
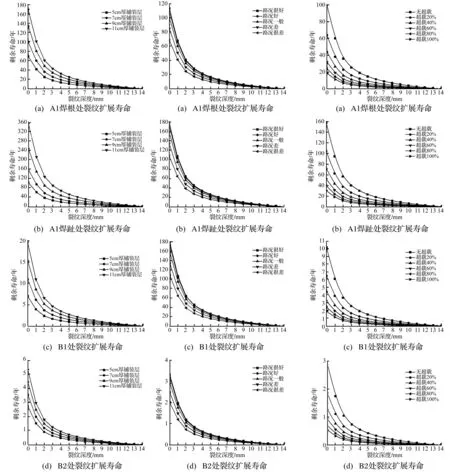
图11 不同铺装层厚度下各疲劳细节裂纹扩展寿命

图14 不同交通量年增长率下各疲劳细节裂纹扩展寿命
4 结 论
(1) 通过实桥算例分析表明,本文所提方法可较好模拟正交异性钢桥面板疲劳裂纹扩展过程。
(2) 疲劳裂纹扩展初期较慢,裂纹深度超3 mm后,裂纹迅速扩展,抵抗疲劳能力较小。
(3) 钢桥各疲劳细节处裂纹扩展寿命受多种因素影响,对交通量年增长率最敏感,交通量年增长率每增加1%,裂纹扩展寿命约缩短一半;车辆超载量60%时,裂纹扩展寿命将缩短至无超载时约一半;路况退化到一般以下后,裂纹扩展寿命迅速缩短;裂纹扩展寿命对桥面铺装厚度变化较敏感,进行钢桥疲劳分析时,不应忽略铺装层作用。
(4) 据本文所求各疲劳细节处裂纹扩展剩余寿命曲线,可合理安排钢桥检测时间,并在检测到裂纹的实际长度后,查此曲线获得其剩余寿命;通过数值模拟方法预测疲劳裂纹扩展路径,为钢桥疲劳裂纹修复及加固提供指导。
[1] 王春生,冯亚成.正交异性钢桥面板的疲劳研究综述[J].钢结构, 2009,24(9):10-14.
WANG Chun-sheng, FENG Ya-cheng, Review offatigue research for orthotropic steel bridge decks[J].Steel Construction, 2009,24(9):10-14.
[2] 童乐为,沈祖炎.正交异性钢桥面板疲劳验算[J].土木工程学报, 2000,33(3):16-21.
TONG Le-wei, SHEN Zu-yan.Fatigueassessment of orthotropic steel bridge decks[J].China Civil Engineering Journal, 2000,33(3):16-21.
[3] Pfei M S, Battista R C.Stress concentrationin steel bridge orthotropic decks[J].Journal ofConstructional Steel Research, 2005, 61(8):1172-1184.
[4] Wu Chong, Ding Wen-jun.Fatigue of orthotropic steel deck under vehicle loads[A].International Symposium on Steel on Steel Structures[ISSS’09][C].Seoul, Koreal, 2009.
[5] 陈斌,邵旭东.正交异性钢桥面疲劳开裂研究[J].工程力学, 2012, 29(12):170-174.
CHEN Bin, SHAO Xu-dong.Study of fatigue cracking for orthotropic steel bridge deck[J].Engineering Mechanics, 2012, 29(12): 170-174.
[6] BS5400: Steel, concrete and compositebridge part 10: code of practice for fatigue[S].1980.
[7] AASHTO LRFD Bridge design specifications[S].2005.
[8] 朱劲松,孟会林.公路钢桥精细化抗疲劳设计方法及其应用[J].桥梁建设,2009,3:44-58.
ZHU Jing-song, MENG Hui-lin.Refined anti-fatigue design methodology and its application for highway steel bridge[J].Bridge Construction,2009,3:44-58.
[9] EN1993-1-9:2005,Eurocode 3: designof steel structures[S].
[10] NEN6788,The designof steel bridge: basic requirements andsimple rules[S].
[11] 日本道路協會.道路橋示方書·同解說[S].日本东京:丸善株式会社,2002.
[12] 崔冰,吴冲,丁文俊.车辆轮迹线位置对钢桥面板疲劳应力幅的影响[J].建筑科学与工程学报,2010,27(3):19-23.
CUI Bing, WU Chong,DING Wen-jun.Influence of acting position of vehicle wheels on fatigue stress range of steel deck[J].Journal of Architecture and Civil Engineering,2010,27(3):19-23.
[13] Kwon K, Frangopol D M.Bridge fatigue reliability assessment using probability density functions of equivalent stress range based on field monitoring data[J].International Journal of Fatigue, 2010, 32:1221-1232.
[14] Lei G, Moe S C.Computer simulation of dynamic interactions between vehicle and long span box girder bridges[J].Tsinghua Science and Technology,2008,13(S1):71-77.
[15] 朱劲松,邑强.中下承式拱桥吊杆应力冲击系数不均匀性研究[J].振动与冲击,2012,31(13):5-10.
ZHU Jing-song, YI Qiang.Non-uniformity of stress impact factor of suspenders on half-through or through arch bridges[J].Journal of Vibration and Shock, 2012,31(13):5-10.
[16] 李庆芬,胡胜海,朱世范.断裂力学及其工程应用[M].哈尔滨:哈尔滨工程大学出版社,2004:52-65.
[17] Paris P C.Erdogan F.A critical analysis of crack propagation laws[J].Journal of Basic Engineering,1963,85(4):528-534.
[18] Yazdani N, Albrecht P.Crack growth rates of structural steel in air and aqueous enviroments, engng[J].Fract Mech, 1989,32(6): 997-1007.
[19] Zhao Yi-shu.Experimental study on mixed mode crack propagation[J].Engineering Fracturemechanics,1989, 34(4): 891-899.
[20] 唐雪松, 赵小鹏.疲劳裂纹扩展行为的跨尺度分析方法[J].工程力学, 2012, 29(10): 20-26.
TANG Xue-song, ZHAO Xiao-peng.Multiscaling analysis approach of fatigue crack growth behavior[J].Engineering Mechanics, 2012, 29(10): 20-26.
[21] 顾萍, 周聪.铁路正交异性钢桥面板典型疲劳裂纹寿命估算[J].铁道学报,2012,34(1):97-102.
GU Ping, ZHOU Cong.Estimation of fatigue life of typical fatigue cracks of orthotropic steel decks of railway bridges[J].Journal of the China Railway Society, 2012,34(1):97-102.
[22] European committee for standardization.design of steel structure part2: steel bridges[S].Brussels: European Committee for Standardization,2006.
[23] 吴冲,刘海燕,张胜利,等.桥面铺装对钢桥面板疲劳应力幅的影响[J].中国工程科学,2010,12(7):39-42.
WU Chong, LIU Hai-yan, ZHANG Sheng-li, et al.Influence of pavement on fatigue stressrange of orthotropic steel deck[J].Engineering Sciences,2010,12(7):39-42.

