基于MED及FSK的滚动轴承微弱故障特征提取

刘志川，唐力伟，曹立军

(军械工程学院 火炮工程系，石家庄 050003)

用于旋转机械中的滚动轴承磨损不可避免，轴承故障会造成机器的振动及噪声，严重时会影响设备正常运行，对滚动轴承故障特征提取、诊断具有重大意义。

谱峭度(Spectral Kurtosis, SK)概念由Dwyer[1]提出，基本原理为计算每根谱线峭度值，而不同峭度值会反应瞬态冲击大小。Antoni等[2-3]将谱峭度值作为短时傅里叶窗口函数，通过谱峭度图选择带通滤波器参数，并提出谱峭度离散算法。文献[4]认为信噪比较高时谱峭度能较好识别瞬态冲击信号。由于轴承工作环境复杂，噪声较大，复杂工况对谱峭度计算值会产生影响，从而对最优带通滤波带宽及中心频率计算产生误差，影响诊断效果，需对微弱故障信号进行降噪预处理。

本文针对谱峭度算法在强噪声干扰时对滚动轴承微弱故障提取能力不足问题，将最小熵反褶积用于微弱信号降噪处理，再对降噪信号进行快速谱峭度计算及故障特征提取，并结合仿真信号与实验数据验证所提方法的有效性。

1 FSK算法

1.1 谱峭度定义

信号x(t)的Wold-Cramer分解在频域表达式为

(1)

式中：H(t,f)为复包络函数，用短时傅里叶变换计算得

(2)

式中：γ(τ)为时间宽度小窗函数，定义Y(t)过程的四阶谱累积量[5]为

(3)

式中：S2n(f)为2n阶谱瞬时矩：

S2nY(f)≜E{|H(t,f)dX(f)|2n}/df

(4)

谱峭度定义为

(5)

峭度大小SK值为关于中心频率及带宽的函数，带宽无限小时SK值为0；带宽过大时SK无法检测出频带范围内的瞬态冲击现象。

快速谱峭度算法(FSK)目的为寻找中心频带与带宽最优组合的滤波器，使含冲击分量的滚动轴承故障信号峭度值达最大。基本原理即合理选择式(2)中短时傅里叶变换的中心频率f与窗宽τ的值，使峭度值达最大，从而更好提取含冲击分量的故障信号。

1.2 FSK仿真应用

滚动轴承发生故障时表现出冲击性，快速谱峭度算法在较小噪声情况下提取故障特征信号效果显著。图1(a)为简单的合成信号，图1(b)为模拟冲击信号，图1(c)为正弦信号。图2为用快速谱峭度方法提取的冲击分量，由图2(a)看出，通过快速谱峭度方法能准确提取含冲击分量的模拟信号，并能定位冲击分量位置；图2(b)为通过能量算子解调法所得冲击信号包络谱，冲击信号频率显示清楚。

图1 仿真信号

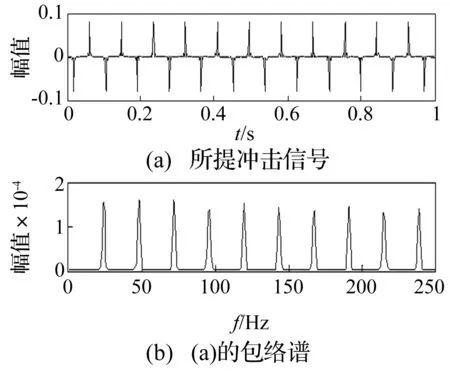
图2 快速谱峭度提取的冲击信号

2 最小熵反褶积

最小熵反褶积(MED)由Wiggins[7]提出，用于提取地震波反射数据。由Endo等[8]将其用于齿轮故障诊断。MED目的为提取信号中较大的尖脉冲成分，而滚动轴承发生故障时伴随有周期性冲击分量，MED较适合滚动轴承信号的前期降噪处理，从强噪声中获取冲击性较大信号。设采集的滚动轴承故障振动信号表达式[9-10]为

y(t)=h(t)x(t)+e(t)

(6)

式中：x(t)为故障脉冲；e(t)为噪声；h(t)为系统传递函数；y(t)为采集的振动信号。

MED目的即寻找逆滤波器w(t)，将采集的振动信号y(t)恢复到冲击信号x(t)，即

x(t)=w(t)y(t)

(7)

(8)

式中：L为逆滤波器w(t)长度。

MED迭代流程见图3，其中A为序列y(t)的L×L自相关矩阵。

图3 MED迭代流程图

(9)

谱峭度方法虽在提取瞬态冲击信号效果较好，但在有强噪声时作用受限。图4(a)为图1(a)简单合成信号加较强噪声污染后的时域图，噪声信号见图4(d)。

图4 带强噪声仿真信号

图5为谱峭度算法提取的冲击信号与冲击信号包络谱图。由图5(a)看出，在强噪声干扰下谱峭度算法难以准确提取冲击信号，图5(b)中所得信号包络谱图亦难以识别冲击信号频率。图6为经MED方法降噪后再经谱峭度滤波提取的冲击信号。由图6看出，用所述方法能成功提取较强噪声干扰的冲击信号，也能清楚识别冲击信号频率。

图5 快速谱峭度提取的冲击信号

图6 速谱峭度提取MED降噪后冲击信号

图7 故障诊断流程图

3 基于MED、FSK的滚动轴承微弱故障特征提取方法

在滚动轴承工作环境复杂、受噪声干扰较大情况下，快速谱峭度算法难以直接提取微弱的轴承故障信号。为提高信号信噪比，突出故障冲击成分，用MED方法对信号进行降噪预处理，再用快速谱峭度算法计算谱峭度图谱，用谱峭度确定最优滤波器的带宽及中心频率，用能量算子解调算法对带通滤波信号进行包络谱分析，克服传统Hilbert包络分析方法时间分辨率低、自适应性差、计算复杂等问题[11]，对比轴承故障频率可获得诊断结果。故障诊断流程见图7。

4 实验验证

滚动轴承内外圈故障实测信号来自二级减速器实验平台，轴承选型号6206深沟球轴承，用线切割在两轴承内、外圈加工细小裂纹作为故障。轴承参数为滚动体个数z=9，滚动体直径d=9.5 mm，轴承中径D=46.5 mm，接触角α=0。信号采集时，振动加速度传感器(B&K4508)固定于齿轮箱故障轴承的轴承座，采样频率10 kHz。轴承故障频率计算式为

内圈

(10)

外圈

(11)

4.1 轴承内圈故障诊断

轴承内圈故障实验时，由JN388型转速转矩传感器测量获得主动轴转速610.2 r/min，中间轴转频fr=5.08Hz，由式(10)计算得轴承内圈故障频率fn=27.55 Hz，采样时间2.5 s。滚动轴承内圈微弱故障时域图见图8，无法获取有效故障特征信息。

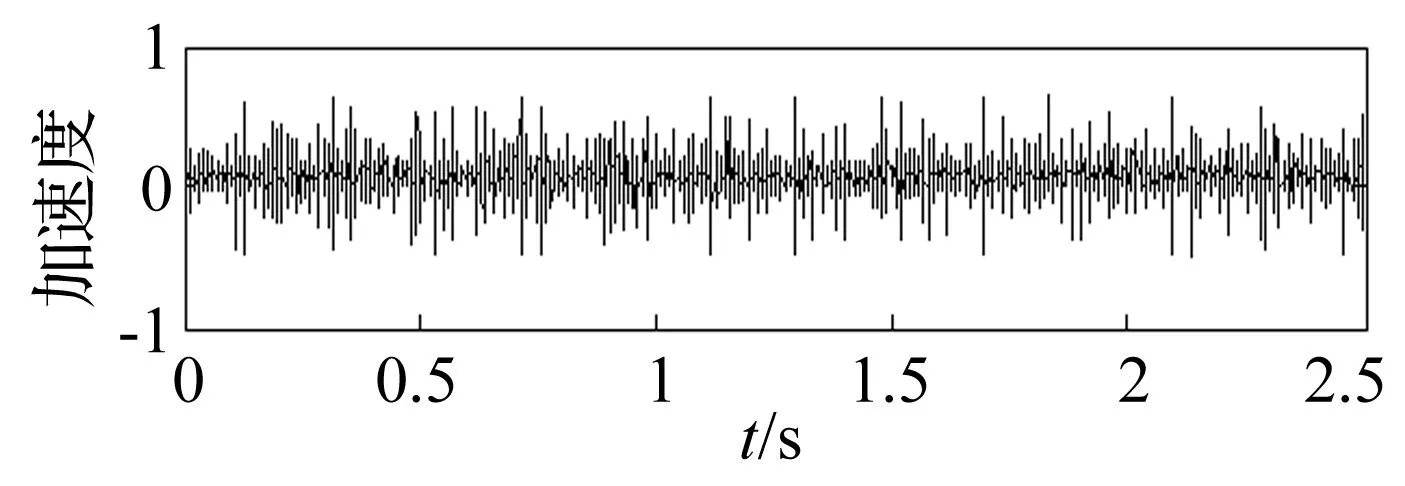
图8 轴承内圈故障信号

原始故障信号直接经谱峭度计算，通过带通滤波所得时域图、包络谱见图9。图9(b)的信号包络谱仍不能识别故障频率。MED降噪后信号及谱峭度带通滤波信号与滤波后信号包络谱见图10。对图10(a)(MED降噪后信号)快速谱峭度谱图见图11。由图11看出，分解层数为3.6时谱峭度值达最大(颜色最深)，最优滤波器带宽416.67 Hz，中心频率208.33 Hz。图10(c)中信号能较好提供轴承内圈故障频率，且倍频及中间轴转频亦体现较好。由此，该方法用于轴承内圈故障诊断得以验证。

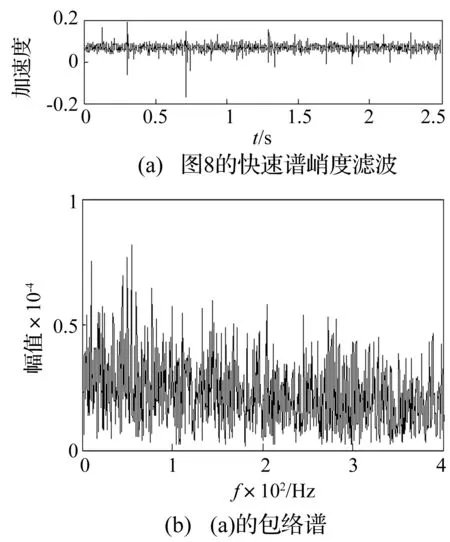
图9 轴承内圈故障信号快速谱峭度滤波

4.2 轴承外圈故障诊断

轴承外圈故障实验时，由JN388型转速转矩传感器测量得主动轴转速1 488.5 r/min，由式(11)计算得内圈故障频率fw=44.41 Hz，中间轴转频fr=12.4 Hz，采样时间2 s。滚动轴承外圈微弱故障时域图见图12，可见无法获取有效的故障特征信息。

图10 MED降噪后信号快速谱峭度滤波

图12 轴承外圈故障信号

原始故障信号直接经谱峭度计算，通过带通滤波获得时域图、包络谱见图13。其中图13(b)中信号包络谱仍不能识别故障频率。图14为MED降噪后信号及谱峭度带通滤波信号与滤波后信号包络谱图。图15为对图14(a)(MED降噪后信号)的快速谱峭度谱图。由图15看出，分解层数为1.6时谱峭度值达最大(颜色最深)，最优滤波器带宽为1 666.67 Hz，中心频率为4 166.67 Hz。图14(c)中信号能较好提供轴承外圈故障频率，且倍频、中间轴转频亦体现较好。由此，该方法在轴承外圈故障诊断中应用得以验证。

图14 MED降噪后信号快速谱峭度滤波

4.3 MED与其它降噪方法对比分析

为验证MED相对传统信号降噪方法更适合强噪声干扰下滚动轴承故障信号的降噪处理，对图13的轴承外圈故障信号分别进行EMD及三层db5小波分解，结果见图16、图17。

图16 EMD分解的IMF1信号分量

图17 小波分解信号

分别对IMF1分量、小波分解信号及MED提取信号进行峭度值计算，结果见表1。由表1看出，通过MED提取的轴承外圈故障信号峭度值明显大于EMD分解及小波分解所得故障信号峭度值，对强噪声干扰的轴承故障信号提取效果更好。

表1 峭度值对比

5 结 论

针对谱峭度方法遇强噪声干扰时难以提取滚动轴承微弱特征信号的不足，本文将最小熵反褶积与快速谱峭度方法综合用于滚动轴承微弱故障信号的特征提取，结论如下：

(1) 用最小熵反褶积(MED)对轴承微弱故障信号降噪预处理，有助于谱峭度算法提取微弱特征信号，能解决快速谱峭度方法不适应强噪声干扰的滚动轴承微弱故障特征提取问题。

(2) 通过谱峭度图选择最优带通滤波器参数，能解决传统轴承故障诊断共振解调方法中滤波器参数难以选择问题。

[1] Dwyer R F.Detection of non-gaussian signals by frequency domain kurtosis estimation[J].Acoustic，Speech and Signal Processing.Boston: IEEE International Conference on ICASSP, 1983,83:607- 610．

[2] Antoni J, Randall R B.The spectral kurtosis: a useful tool for characterizing non-stationary signals[J].Mechanical Systems and Signal Processing, 2006,20(2):282-307．

[3] Antoni J.Fast computation of the kurtogram for detection of transient faults[J].Mechanicall Systems and Signal Processing,2007,20(1):108-124.

[4] 石林锁,张亚洲,米文鹏.基于WVD的谱峭度法在轴承故障诊断中的应用[J].振动、测试与诊断, 2011, 31(1):27-31．

SHI Lin-suo, ZHANG Ya-zhou, MI Wen-peng.Application of Wigner-Ville-Distribution-based spectral kurtosis algorithm to fault diagnosis of rolling bearing[J].Journal of Vibration, Measurement and Diagnosis, 2011,31(1):27-31.

[5] 彭畅,柏林,谢小亮.基于EEMD、度量因子和快速谱峭度图的滚动轴承故障诊断方法[J].振动与冲击，2012,31(20):143-146.

PENG Chang, BO Lin, XIE Xiao-liang.Fault diagnosis method of rolling element bearings based on EEMD，measure-factor and fast kurtogram[J].Journal of Vibration and Shock,2012,31(20):143-146.

[6] 王宏超,陈进,董广明,等.基于快速kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J].振动与冲击,2013,32(1):35-37.

WANG Hong-chao, CHEN Jin, DONG Guang-ming, et al.Application of resonance demodulation in rolling bearing fault feature extraction bsed on fast computation of kurtogram[J].Journal of Vibration and Shock,2013,32(1): 35-37.

[7] Wiggins R A.Minimum entropy deconvolution[J].Geoexploration, 1978,16(1/2):21-35.

[8] Endo H, Randall R B.Application of a minimum entropy deconvolution filter to enhance autoregressive model based gear tooth fault detection technique[J].Mechanical Systems and Signal Processing, 2007,21 (2):906-919.

[9] 王宏超,陈进,董广明.基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J].机械工程学报,2013,49(1):88-94.

WANG Hong-chao, CHEN Jin, DONG Guang-ming.Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition[J].Journal of Mechanical Engineering, 2013,49(1):88-94.

[10] Sawalhi N, Randall R B, Endo H． The Enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis[J] Mechanical Systems and Signal Processing,2007,21: 2616-2633．

[11] 张文义,于德介,陈向民.基于信号共振稀疏分解与能量算子解调的轴承故障诊断方法[J].中国电机工程学报,2013,33(20):111-118.

ZHANG Wen-yi, YU De-jie, CHEN Xiang-min.Fault diagnosis of rolling bearings based on resonance-based sparse signal decomposition and energy operator demodulating[J].Proceedings of the CSEE, 2013,33(20):111-118.