模态测试中力传感器附加质量辨识及消除方法研究
任 军,毕树生
(北京航空航天大学 机器人研究所,北京 100191)
模态测试中的附加机械影响,如传感器附加质量影响[1-3]、结构支撑引入的附加刚度(及阻尼)影响[4-6]以及激振顶杆附加弯曲刚度影响[7-8]等通常使所测频响函数不准确;而传感器附加质量影响主要源于加速度传感器与力传感器。对消除加速度传感器附加质量方法,Decker等[9]基于子结构技术及利用频响函数进行结构动力学修改方法研究消除加速度传感器附加质量影响。Ashory[10]基于直接子结构技术(SMURF方法)用两不同质量加速度传感器测量消除跨点频响函数中传感器附加质量影响。Carkar等[2]基于谢尔曼-莫里森公式研究由所测频响函数中消除加速度传感器质量影响方法;但针对力传感器附加质量影响研究较少。
虽为测试带来附加质量影响,但力传感器较加速度传感器不同。见图1,加速度传感器产生的附加质量位于被测结构的响应点处,而力传感器位于结构激振点处;加速度传感器产生的附加质量大小较易获得(等于自身质量),而力传感器因自身结构的特殊性,其附加质量(图1力传感器网格部分)仅为自身总质量的一部分,大小未知。且力传感器在安装过程中亦会引入安装附件质量,该因素均使实际附加质量难以准确获知;因此,本文提出基于测量的频响函数辨识力传感器附加质量方法。分析附加质量对结构频响函数的修改,在此基础上推导用所测频响函数表达附加质量的通用公式;通过数值仿真验证方法的可行性;采用激振器+激光测振仪(测量的速度响应)测试方案对简支梁进行模态实验,并基于测量的频响函数对力传感器附加质量进行辨识。

图1 悬臂梁模态测试示意图
1 附加质量消除及辨识原理


图2 附加质量对结构动力学修改
对图2(a),较易获取A,B点位移及作用力FB在频域内关系式为
(1)
(2)
在B点添加质量m后(图2(b))得
XA=HABFB+HABRB
(3)
XB=HBBFB+HBBRB
(4)
式中:RB为附加质量m对结构体B点产生的作用力。对附加质量m自身,也可建立位移Xm与其所受反作用力Rm间关系式
Xm=HmmRm
(5)
式中:
(6)
B点位移及力约束条件分别为
XB=Xm,RB+Rm=0
(7)
联立式(1)~式(7),得
(8)
(9)
式(9)即为消除力传感器附加质量影响的基本公式,与文献[1]结论一致。
同样,激励点移至A点时(图2(c)),得
(10)
据模态理论的互易性原理,HAB与HBA相等。因此,可分别取式(9)中HAB及式(10)中HBA建立等式求解
(11)
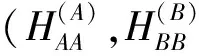
(12)
将式(12)表示成通用形式
Am=B
(13)
由于A,B均为关于ω的函数,可在整个测量频段取多个值,因此,式(13)为关于m的超静定方程,采用最小二乘法将其转换为定解方程求解得
ATAm=ATB
(14)
式中:AT为A的共轭转置。将所得附加质量m值代入式(9)、(10)即可对所测频响函数进行修正。
2 数值仿真
图3为悬臂梁模型,物理参数见表1。悬臂梁沿长度方向离散成6等份,选第2、4点为分析点。设力传感器的附加质量为0.5 kg。
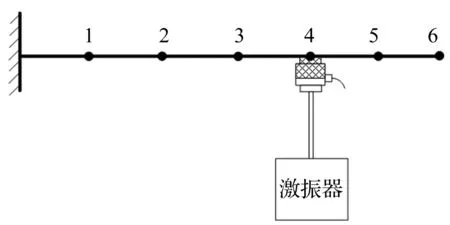
图3 悬臂梁模型

表1 悬臂梁物理参数
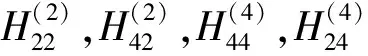

图4 频响函数曲线
3 实验验证
为准确辨识力传感器附加质量,实验中应尽量避免除力传感器外的其它传感器附加质量影响。因此用激光测振仪取代传统的加速度传感器测量响应信号。激光测振仪测量精度高,且其非接触式测量方式可避免额外质量影响[11]。据式(11),实验中需先后对两个不同测点进行激振,本实验用可移动式支架,激振器通过软弹性绳悬挂在支架上。考虑传统刚性激振顶杆会给测试引入一定附加弯曲刚度,故采用钢丝预紧激振方式[12]取代刚性顶杆激振,最大程度消除顶杆的附加弯曲刚度影响。

图6 简支梁模态测试试验
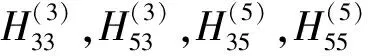
(15)
因激光测振仪测量速度信号,而式(15)所用为位移频响函数,速度频响函数与位移频响函数间仅存在jω倍数关系。故将式(15)左右同乘jω得
(16)
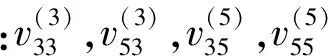

图7 所测频响函数及相干函数(3、5测点)
由于简支梁安装中引入的结构非线性及测试中噪声,所测频响函数受到影响(图7)。4组频响函数各自在不同频段出现“波动”或“毛刺状”曲线,且该频段对应的相干函数值亦较低,说明频响函数精度较差。而据式(16),附加质量m的辨识精度直接取决于4组频响函数的测量精度。因此频响函数数据参与计算必会影响m的辨识精度。而由分析可知,理论计算所得m值在整频段均相等。故可只选数据质量较高的频段参与计算(应保证4组频响函数在所选公共频段均有较高质量)。频段选取原则可考虑两方面:① 频响函数曲线应光顺、无“毛刺”;② 频段应具有较高相干函数值。为此,本实验选95~150 Hz及280~330 Hz频段数据参与计算,见图8、图9。
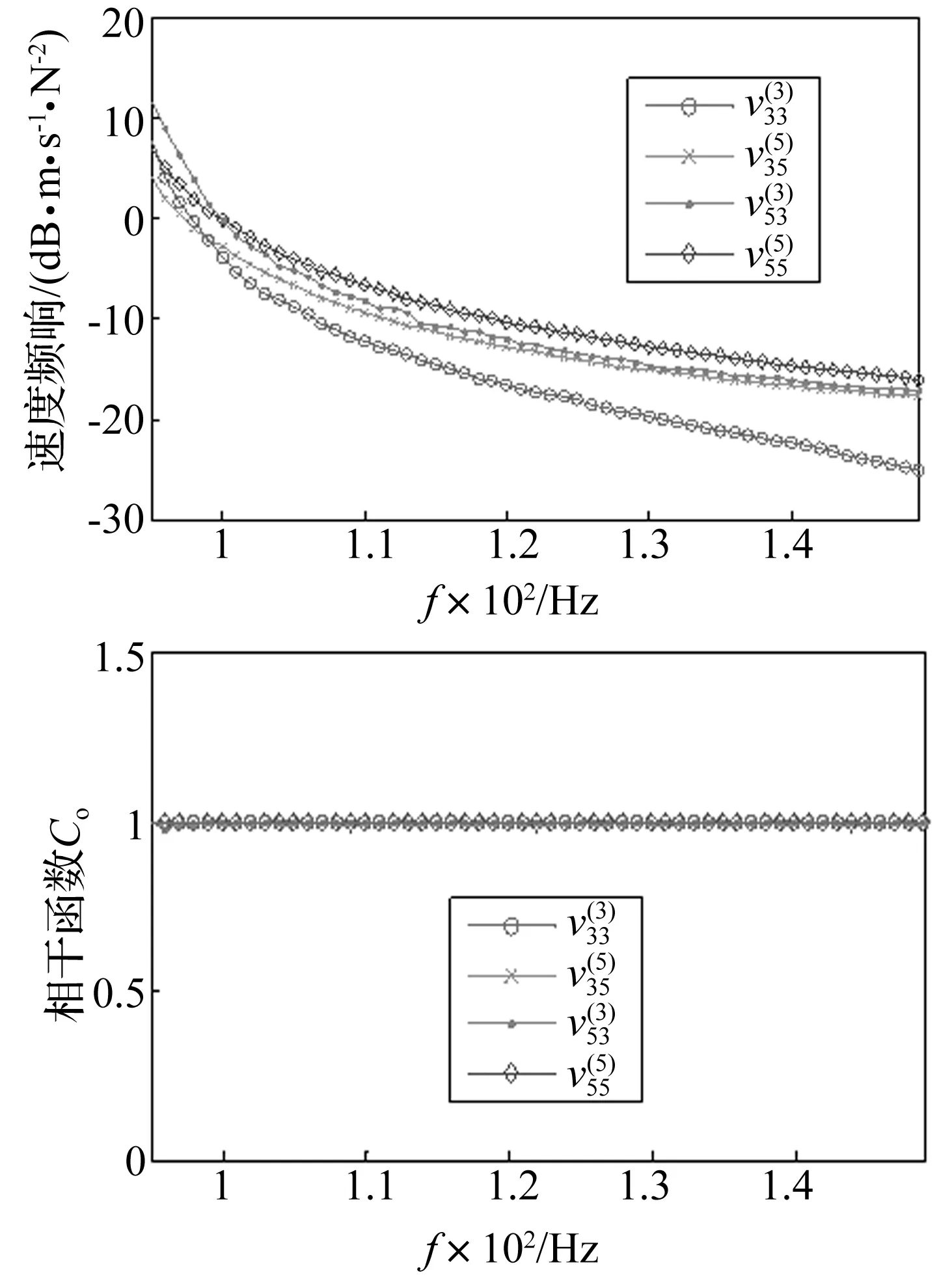
图8 参与计算频段(95~150 Hz)

图9 参与计算频段(280~330 Hz)
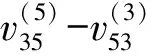

图10 附加质量m辨识结果(95~150 Hz)

图12 所测频响函数及相干函数图(5、6测点)

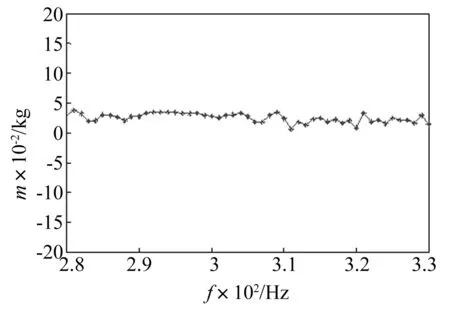
图13 附加质量m辨识结果(280~330 Hz)
4 结 论
(1) 本文提出的基于测量的频响函数辨识力传感器附加质量方法,通过测量两组驱动点、跨点频响函数辨识力传感器附加质量大小,进而为频响函数修正或动力学模型修改提供重要依据。
(2) 该方法辨识精度取决于频响函数测量精度,应尽量减少测量中噪声对频响函数的干扰。实验中较难保证频响函数在全频段均具有高质量时,可针对性选4组频响函数中质量均较高的公共频段数据参与计算,以提高辨识精度。
(3) 本文附加质量辨识方法,理论上只需任取两不同测点进行频响函数测量,但实际中应合理选择两测点以尽可能“弱化”测量误差对辨识结果影响。
[1] Bi Shu-sheng, Ren Jun, Wang Wei, et al.Elimination of transducer mass loading effects in shaker modal testing[J].Mechanical Systems and Signal Processing,2013,38(2):265-275.
[2] Cakar O, Sanliturk K Y.Elimination of transducer mass loading effects from frequency response functions[J].Mechanical Systems and Signal Processing, 2005,19(1):87-104.
[3] Ewins D J.Modal testing: theory, practice and applications, 2nd edition[M].England: Research Studies Press, 2000.
[4] REN Jun, BI Shu-sheng, WANG Wei,et al.Elimination of support effects in modal testing[C].Shanghai, China: Trans Tech Publications, 2012:48-51.
[5] Fayyadh M M, Razak H A, Khaleel O R.Differential effects of support conditions on dynamic parameters[J].Procedia Engineering,2011, 14: 177-184.
[6] Ren Jun, Bi Shu-sheng, Wang Wei, et al.Elimination of multi-points support effects in modal testing[C].Xiamen, China: Trans Tech Publications, 2013:79-84.
[7] Avitabile P.Can the shaker stinger have any effect on the frequency response measurements?[J].Experimental Techniques, 2010, 34(3):11-12.
[8] Cloutier D, Avitabile P, Bono R, et al.Shaker/stinger effects on measured frequency response functions[C].Orlando, FL, United states: Springer New York, Society for Experimental Mechanics (SEM), 2009.
[9] Decker J, Witfeid H.Correction of transducer-loading effects in experimental modal analysis[C].Proceedings of the 13th International Modal Analysis Conference,1995.
[10] Ashory M R.Correction of mass-loading effects of transducers and suspension effects in modal testing[C].USA, Proceedings of the 16th International Modal Analysis Conference,1998: 815-828.
[11] Warren C, Niezrecki C, Avitabile P, et al.Comparison of FRF measurements and mode shapes determined using optically image based, laser, and accelerometer measurements[J].Mechanical Systems and Signal Processing,2011, 25(6): 2191-2202.
[12] Peres M A, Bono R W.Practical aspects of shaker measurements for modal testing[C].University of Cincinnati-SDRL,2010.

