含间隙高速多连杆传动机构动力学特性研究

张增磊，巫世晶，赵文强,2，王晓笋

(1.武汉大学 动力与机械学院，武汉 430072；2.河南平高电气股份有限公司，河南 平顶山 467001)

间隙作为机械系统典型特征对高速重载传动机构运动学及动力学响应会产生深度影响，使传动机构呈现强烈非线性振动特性。对含转动副间隙机构进行动态特性研究前提为对其建立准确、高效动力学模型[1-2]。通过大量理论与实验研究探索转动副间隙对传动机构动态特性影响，并按不同假设形成不同的建模理论与方法，主要有三种，即基于接触-分离的二状态模型[3-5]、基于接触-分离-碰撞的三状态模型[6-9]及基于连续接触的连续接触模型[10-15]。连续接触模型较简单，较难反映副元素间动力学特性；三状态模型较复杂，且不能求解接触碰撞力；二状态模型在模型精确性或求解难度均符合实际需要，在二状态模型基础上逐渐发展成为碰撞铰模型[16]。

本文基于间隙矢量模型，考虑构件制造、装配误差建立高速多连杆传动机构含间隙转动副的碰撞铰模型，并用非线性弹簧阻尼模型描述运动副元素法向接触力与位移关系，用修正的库伦摩擦模型描述运动副元素切向摩擦力与位移关系，建立该传动机构动力学模型，并嵌入ADAMS软件，分析转动副间隙对该传动机构动力学特性影响。

1 动力学建模

1.1 间隙矢量模型

将转动副间隙嵌入系统动力学模型为含间隙机构动力学建模关键。本文用间隙矢量模型能合理描述转动副间隙并能将其引入系统动力学模型，即在含间隙转动副中引入间隙矢量，并通过间隙矢量描述含间隙转动副元素间相对运动关系，相邻构件间精确相对位置变化用间隙矢量表示，可有效处理因构件制造误差所致连接点相对位置变化。

图1 间隙矢量模型

间隙矢量定义在浮动局部笛卡尔坐标系中，起点为轴套中心，终点为轴颈中心，方向为轴颈与轴套在机构运行中可能发生碰撞的点，间隙矢量大小限制在以轴承中心为圆心的间隙圆内，间隙圆半径为轴与轴承半径之差，因此构件的相对运动状态可由间隙矢量大小变化反映，且亦能反映间隙运动副元素是否接触，见图1。

1.2 含间隙转动副模型

因制造误差、装配要求及磨损等因素，间隙不可避免存在于实际机械系统转动副中。间隙的存在使轴颈与轴套并非同心，会产生半径方向的偏心距eij；因磨损、挤压变形等，间隙变化呈随机性，轴颈与轴套相对位置不会随时确定，从而影响间隙转动副运动学、动力学行为，使分析变得复杂。为描述间隙动态变化及不确定性所致动力学影响，基于间隙矢量模型对间隙转动副建模。设相邻构件间只通过转动副连接，则间隙被定义为轴颈与轴套在配合位置的半径差；认为间隙转动副元素间存在分离、接触及穿透三种状态。含间隙转动副模型见图2。

图2 含间隙转动副模型

在图2模型中，ei表示轴颈相对轴套偏心距，计算式为

(1)

径向间隙为常量，定义为

c=ri-ri+1

(2)

式中：ri，ri+1分别为构成转动副的轴套、轴颈半径。

因碰撞产生的接触变形可表示为

δi=ei-c

(3)

可据接触变形大小确定转动副元素处于分离、接触或穿透状态。图2 (a)为分离状态，此时轴颈与轴套并未接触，轴颈可在轴套边界内自由运动；图2(b)为接触状态，此时轴颈与轴套恰好接触，为分离状态结束或穿透状态开始时刻；图2(c)位穿透状态，此时轴颈与轴套间产生弹性变形，两者时刻保持接触。接触碰撞法向力Fn与切向力Ft计算式为

(4)

式中：K为接触刚度系数；δn为接触时轴颈与轴套相对穿透深度；m为非线性弹性接触力指数，与材料特性密切相关；Cn，Ct分别为法向、切向粘滞阻尼系数；f为摩擦系数；Vt为副元素间相对滑移速度；sign(Vt)为滑移速度符号函数，用于判断摩擦力方向。

接触刚度系数与接触面形状及物理属性密切相关，计算式为

(5)

(6)

式中：hk为与材料属性相关系数；μk，Ek分别为副元素所在构件泊松比及弹性模量；ri，ri+1分别为接触处副元素曲率半径。

1.3 实际机构动力学建模

用间隙矢量模型建立转动副间隙动力学模型后便可将其用于实际机械系统。本文研究某高压断路器中用于分合闸动作的连杆驱动机构，结构简图见图3。驱动力作用于接头连杆1使其在水平滑槽内运动，经中间杆件运动及传递力，通过动触头连杆9与静触头接触碰撞，推动静触头运动至合闸位置，实现断路器合闸动作。

图3 多杆传动机构简图

该机构为具有1个自由度的平面10杆机构，包括两定轴转动构件连杆3、连杆7及3个只能平动构件连杆1、5、9，其余4构件作平面运动。该机构亦可分解为4个类似曲柄-滑块机构的子机构，分别为机构A、B、C、D。分别对每个子机构建立动力学模型，通过公用参数将其联合即可。

以机构A为例，其局部放大带转动副间隙模型见图4。考虑3个转动副均存在间隙最复杂情况、不计移动副与机架间摩擦建立动力学方程。考虑单个或两个间隙时，只需在改组方程基础上适当简化即可。3杆件长度分别为li(i=1,2,3)，对应质量分别为mi(i=1,2,3)，质心位置分别为Si(i=1,2,3)；轴颈半径分别为Ri(i=1,2,3)，轴颈与轴套中心距分别为ei(i=1,2,3)，即所建间隙矢量。将间隙矢量ei(i=1,2,3)分别向x，y轴投影，其分量可表示为

(7)

式中：ls1为连杆1质心与点O1间距；ls2为连杆2质心与其轴颈圆心之距；ls3为连杆3质心与其轴颈圆心之距；θi(i=1,2,3)分别为3分杆件相对x轴倾角。

间隙矢量与x轴夹角计算式为

(8)

接触点处作用力分解到x，y轴的分力为

(9)

式中：Fin，Fit分别为接触点处法向碰撞力及切向摩擦力。

图4 含多间隙转动副机构A模型

建立机构A的运动微分方程为

(10)

式中：各参数物理含义均同上。将上述各式联立化简得

(11)

2 模型求解及结果分析

将所建机构碰撞接触模型通过GFORCE用户分析子程序嵌入ADAMS中用Gear法进行求解，时间步长0.001 s，可得该传动机构动态特性。连杆1作为机构运动驱动杆，在输入力作用下将按一定规律运动。设其运动特性已知，并按规律进行：

(12)

式中：x为连杆1位移，变化范围0～-0.23 m；T为运动时间，变化范围0～0.085 s。初值xs1为已知,各杆件初始转角θi按图3测得，其它参数待求。xs1的变化曲线见图5，速度特性为先加速后减速，保证动触头以较小速度与静触头碰撞。

考虑所有转动副处均存在间隙，共10个间隙转动副，间隙大小均为0.1 mm。各连杆长度、惯性参数见表1，动力学仿真参数见表2。

图5 输入位移及速度特性曲线

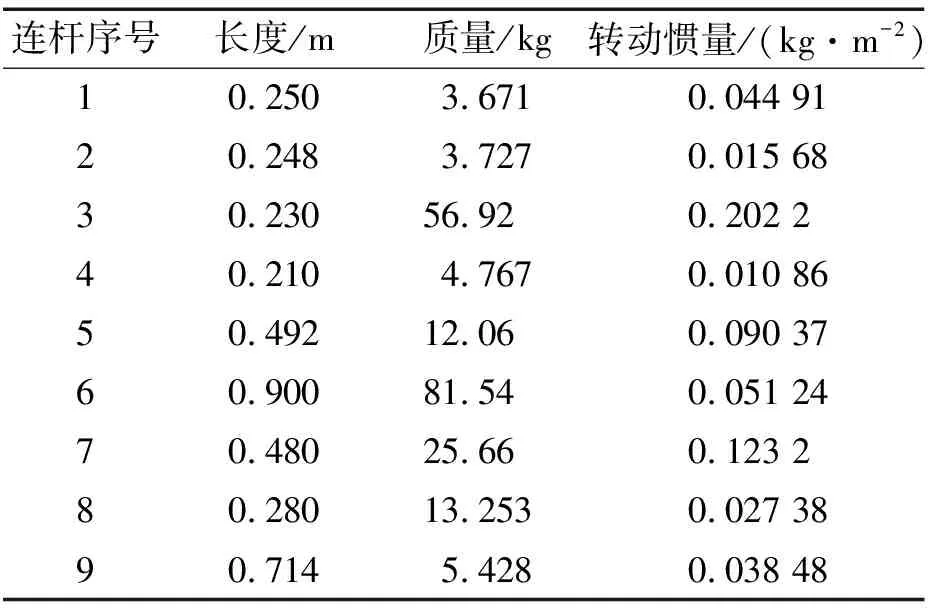
表1 机构各连杆特征参数

表2 仿真计算参数

仿真所得输出端运动特性曲线见图6。由图6看出，考虑间隙时动触头输出位移特性曲线与理想模型基本重合；动触头输出速度特性曲线与理想模型基本相同；但存在两个阶段，理想模型与转动副间隙模型特性不一致，即间隙存在时速度有一定滞后性及波动性，分别发生在机构开始运动阶段、机构减速阶段；加速度特性与动触头转动副处反力呈较大不同，即瞬时冲击效应伴随一定波动性，最大瞬时加速度高达11 000 m/s2，对应的冲击力超过50 000 N，对机构正常稳定运行影响较大。需研究影响该机构运行因素，以提高机构运行可靠性。

图6 动触头输出运动特性曲线

3 动态特性影响参数分析

影响多连杆传动机构(图3)动态特性因素较多，包括材料属性、零件加工精度、润滑及磨损变形等。考虑由多种因素引起的不同间隙大小对机构动态特性影响。由含间隙机构与理想机构运动特性对比结果看出，间隙对位移特性影响较小，可忽略；而对速度、加速度均有不同程度影响，亦可从加速度特性中发现转动副反力的变化规律。由于机构整个运动过程中考虑间隙时速度特性曲线与加速度特性曲线与理想模型基本相同，仅在运动起始阶段与减速阶段含间隙机构动态特性会有明显不同，在运动起始阶段对比效果最明显。因此取动触头运动开始0.01 s内的动态特性进行对比分析。通过设定不同因构件制造、装配误差所致间隙值分析间隙大小对动触头在合闸过程时速度、加速度特性影响。考虑间隙尺寸分别为0.01 mm、0.03 mm、0.05 mm及0.1 mm时将机构动态特性与理想模型进行对比。

不同间隙大小时速度特性对比见图7。由图7看出，运动起始阶段理想速度特性曲线为规则光滑上升曲线，而含间隙机构速度特性则出现较大差异，主要在时间上的滞后效应，并随间隙变化而变化。随间隙的增大，速度在时间上的滞后效果愈加明显，且波动效应更强烈，导致与理想速度特性曲线趋于一致的时间变长。尤其间隙为0.1 mm时，动触头开始运动速度滞后时间近0.004 s，趋于稳定时间为0.008 s。虽时间较短，但相对特高压断路器连杆驱动机构的高速重载特性而言，会造成约9.4%的运行误差，产生巨大负面作用，甚至造成严重事故。

不同间隙大小时加速度特性对比见图8。由图8看出，加速度特性存在随间隙增大而增强的滞后效果；加速度在运动起始阶段会呈现强烈的冲击效应，具有较高的瞬时峰值，且随间隙增大冲击效应越明显，与理想加速度特性曲线趋于一致的时间亦增长。尤其间隙为0.1 mm时，动触头瞬时冲击加速度高达11 000 m/s2，表明动触头转动副元素间存在剧烈接触碰撞，产生巨大碰撞冲击力，使机构在实际运行中产生强烈振动，甚至使机构零部件断裂失效，导致严重事故。

图7 不同间隙大小时速度特性对比

通常在含单个间隙转动副机构(如曲柄滑块机构或曲柄摇杆机构)中，较难发现明显的速度特性与加速度特性滞后效应。由分析知此两种效应由多个间隙转动副对机构动态特性影响叠加形成。在一个间隙转动副中，间隙尺寸相对副元素尺寸较小，较难对机构动态特性产生较大影响，但当间隙转动副数量增加时，由间隙造成的机构整体传递误差会变明显。尤其在高速重载传动机构中，机构完成传动任务所需时间很短，故由多处间隙共同作用造成运动时间差异不能忽略。

轴颈与轴套运动副元素相对运动关系见图9。由图9看出，运动开始前轴颈相对轴套位置并不确定，设其初始位置在A点，而轴颈与轴套在特定驱动下的潜在接触位置在B点，则轴颈需一段时间由A运动到B。间隙增大时，在相同时间内轴颈获得速度增大；设碰撞时间相同，碰撞瞬间加速度、碰撞力均会增大(图6、图8)。对本文研究的平面10杆机构，考虑同时存在十个间隙转动副，由该副元素初始位置与潜在接触位置不重合所致误差会增加，因而会出现机构运动特性(图6～图8)。

针对由多间隙转动副共同作用导致多连杆传动机构运行不稳定性，可用的减小振动、提高传动精度方法有两种，即适当提高机构加工精度以减小间隙尺寸及在转动副元素尺寸较大处(连杆3、7与机架连接位置)，用滚动轴承连接连杆与机架以减少含间隙转动副数量。

4 结 论

(1) 研究转动副间隙建模方法基础上，基于间隙矢量模型，建立间隙转动副的碰撞铰模型，利用非线性弹簧-阻尼模型计算接触法向力，利用修正的库伦摩擦模型计算接触切向力。

(2) 针对高压断路器中高速多连杆传动机构，将碰撞铰模型引入机构动力学模型，在特定工况下仿真获得机构运动特性，发现间隙对速度、加速度有重要影响。

(3) 分析间隙在不同尺寸时的机构动态特性，发现随间隙的增大机构速度、加速度特性中滞后及加速度特性中冲击效应增强，该现象在低速简单机构中较难发现，此原因为多间隙转动副共同作用及该机构高速特点所致。

(4) 对高速多连杆传动机构，可适当减小初始设计间隙值，亦可通过用滚动轴承代替部分含间隙转动副方法降低机构运行的冲击及振动，有利于提高系统可靠性。

[1] Dubowsky S, Freudenstein F.Dynamic analysis of mechanical systems with clearance, part 1:formation of dynamic model[J].ASME Journal of Engineering for Industry, 1971,93(1):305-309.

[2] Dubowsky S, Freudenstein F.Dynamic analysis of mechanical systems with clearances, part 2: dynamic response[J].ASME Journal of Engineering for Industry, 1971,93(1):310-316.

[3] Dubowsky S, Gardner T N.Dynamic interactions of link elasticity and c1earnce connections in planar mechanical systems[J].Journal of Manufacturing Science and Engineering,1975,97(2): 652-661.

[4] Dubowsky S, Gardner T N.Design and analysis of multilink flexible mechanisms with multiple clearance connections[J].Journal of Manufacturing Science and Engineering,1977,99(1):88-96.

[5] Dubowsky S, Norris M, Aloni E, et al.An analytical and experimental study of the prediction of impacts in planar mechanical systems with clearances[J].Journal of Mechanical Design,1984, 106(4):444-451.

[6] Funabashi H,Ogawa K,Horie M, et al.A dynamic analysis of the plane crank and rocker mechanisms with clearances[J].Bulletin of the JSME,1980,23(177):446-452.

[7] 余跃庆,李哲.现代机械动力学[M].北京：北京工业大学出版社,1998.

[8] 李哲.考虑运动副间隙和构件弹性的平面连杆机构动力学研究[D].北京：北京工业大学,1991.

[9] 唐锡宽,金德闻.机械动力学[M].北京：高等教育出版社,1984.

[10] Miedema B, Mansour W M.Mechanical joints with clearance: a three-mode model[J].Journal of Engineering for Industry,1976,98:1319-1323.

[11] Mansour W M, Townsend M A.Impact spectra and intensities for high-speed mechanisms[J].Journal of Engineering for Industry,1975,97(1):347-353.

[12] Soong K, Thompson B S.A theoretical and experimental investigation of the dynamic response of a slider-crank mechanism with radial clearance in the gudgeon-pin joint[J].Journal of Mechanical Design,1990,112(2):183-189.

[13] 张策.含间隙曲柄摇杆机构阶段运动模型的建立[C].//第五届机械传动年会论文集,上海,1992.

[14] Earles S W E,Wu C L S.Motion analysis of a rigid-link mechanism with clearance at a bearing, using lagrangian mechanism and digital computation[C].Conference on Mechanisms, IME, London, England,1972:83-89.

[15] Furuhashi T, Morita N, Matsuura M.Research on dynamics of four-bar linkage with clearances at turning pairs(including four reports)[J].Bulletin of the FSME, 1978, 21:518-523.

[16] 王国庆.考虑碰撞、非线性阻尼和构件弹性的机构动力学理论与应用研究[D].西安：西安理工大学,2002.