一种面向SIFT特征匹配的过滤新算法

蒋中杰，程筱胜，崔海华，张益华

(南京航空航天大学 机电学院，江苏 南京 210016)

一种面向SIFT特征匹配的过滤新算法

蒋中杰，程筱胜，崔海华，张益华

(南京航空航天大学 机电学院，江苏 南京 210016)

针对SIFT匹配算法存在误匹配的情况，提出了一种基于三角形相似的匹配特征点过滤算法，即在SIFT算法中使用欧式距离判断特征点相似性后，对匹配的特征点构造三角形，通过判别三角形相似对匹配特征点进行进一步过滤。实验结果表明，三角形相似算法能大大提高匹配精度。

图像拼接；SIFT算法；三角形相似；匹配点过滤

图像配准是对有重叠区域的图像进行匹配，进而获得图像间位置关系的分析处理技术。图像配准在很多行业都有着广泛的应用。但是在实际应用中，需要匹配的两幅图像之间通常存在着平移、旋转、尺度、视角等差异，这些都是图像配准会碰到并需要解决的问题。图像匹配算法中，基于灰度相关匹配算法(如SSDA，MMSE等)的主要缺点是当图像发生旋转、视角、尺度、亮暗变化时，算法会很不稳定；而基于特征的图像匹配算法(例如SIFT，Harris等)对图像几何变形、亮暗变化都有很高的鲁棒性。目前图像配准的主要研究方向都集中在基于特征的图像配准。文献[1]、[2]对几种具有代表性的基于特征的图像匹配算法进行了研究，发现SIFT算法是鲁棒性最高的特征匹配算法。

虽然SIFT算法已经在很多领域被成功应用[1-3]，但是SIFT算法在匹配精度上还有很大改进空间。文献[4]将SIFT算法和RANSAC算法结合以去除不可靠的匹配点，可惜的是RANSAC算法虽然能滤除大部分的误匹配点，但却不能保证去掉所有的误匹配点。文献[5]、[6]提出了双向匹配的滤除策略，但是双向匹配需要自定义阈值。文献[7]对图像增加了彩色信息，可是在增加了彩色信息后，滤除的匹配点会比较多，在图像少特征点的情况下可能导致图像无法匹配。

本文提出了一种基于三角形相似的过滤新算法，通过判断三角形相似甄别匹配点是否正确。与其他过滤算法相比，三角形相似法过滤的特征点较少，但是正确率却会大大提高。

1 SIFT算法

SIFT匹配算法流程主要由4步构成：构建高斯尺度空间、特征点检测、特征点描述符生成和特征匹配[8-9]。

1.1尺度空间特征点

文献[10]证明了高斯核函数是可以实现尺度变化的唯一核函数。采集的图像经过不同尺度高斯模糊，将采样生成N层高斯尺度空间金字塔，然后将高斯尺度空间金字塔中每一层的图像再做不同参数的高斯模糊，使得高斯尺度空间金字塔每一层都有多张图像，其中同一层的图像大小相同。然后把同层高斯尺度空间金字塔中的相邻金字塔层图像相减，得到DoG(Difference of Gaussian，简称DoG算子)差分金字塔。DoG差分空间函数D(x,y,σ)定义如下：

D(x,y,σ)=(G(x,y,kσ)-G(x,y,σ)×I(x,y))=L(x,y,kσ)-L(x,y,σ)

式中：G(x,y,σ)为高斯函数(尺度可变)；I(x,y)为原始图像；L(x,y,σ)为经过高斯模糊的图像；k为不变尺度比例因子；σ为高斯尺度。

DoG差分金字塔建立后，比较每个像素点的周围8个像素点，以及它相邻尺度图像中的各9个像素点。如果该点为极值点，那么把该点作为候选特征点。

1.2特征点精确定位

通过上述方法检测到的极值点是离散空间的极值点，由于DoG算子会产生较强的边缘响应，所以通过拟合三维二次函数来精确确定关键点的位置和尺度，去除低对比度的关键点和不稳定的边缘响应点，能增强匹配稳定性，提高抗噪声能力。

1.3特征点主方向

为了让描述子具有旋转不变性，需要利用局部特征为特征点确定一个方向。利用图像梯度，可求得特征点的方向。梯度的幅值与方向角计算公式如下：

m(x,y)=[L(x+1)-L(x-1,y)]2+[L(x,y+1)-L(x,y-1)2]1/2

式中：m(x,y)为梯度幅值；θ(x,y)为梯度方向。

完成特征点的梯度值计算后，用直方图统计出领域像素梯度和方向。梯度直方图把360°的方向范围平均分成36柱。直方图的梯度幅值中的峰值代表特征点的主方向。同时保留其他梯度幅值大于主方向梯度幅值80%的作为辅方向。特征点可以有多个方向。

1.4计算特征点描述子

(1)选取特征点领域，然后把选取的邻域均匀地分为4×4个窗口，对每个窗口计算梯度方向直方图。(2)对4×4个窗口的8个方向的梯度直方图以位置依次排序，得到一个4×4×8共128维的向量，这个向量是图像信息的一种表示，是具有唯一性的。(3)把特征描述子归一化，除去亮暗变化的影响，最终得到对尺度变化、亮暗变换和旋转有较高鲁棒性的SIFT局部特征描述子。

1.5特征点匹配

因为特征点可能有较强的独特性，其匹配点对特征向量的欧式距离较大是正常的。一种比较有效的方法是在匹配时比较与关键点的特征向量最近的和次近的关键点。取图像1中的某个关键点，并找出其与图像2中欧式距离最近的前2个关键点，在这2个关键点中，如果最近的距离除以次近的距离少于某个比例阈值，则接受这一对匹配点。

2 基于三角形相似的过滤算法

为了排除因为图像遮挡和背景混乱而产生的无匹配关系的关键点，Lowe提出了比较最近邻距离与次近邻距离的方法，距离比率ratio小于某个阈值的认为是正确匹配。因为对于错误匹配，由于特征空间的高维性，相似的距离可能有大量其他的错误匹配，从而导致它的ratio值比较高。Lowe推荐ratio的阈值为0.8。本文针对特征点比较少的牙模图像进行拼接，比例阈值选取0.9。特征点数目较多时，误匹配也较多。

2.1三角形定义

三角形由2个基本点和1个变换点构成。经过欧式距离法后，两幅图像中的匹配点分别在点集P和点集Q中。在点集P中的每一个特征点，在点集Q中都有特征点与之对应。在点集P中随机选取2个特征点P1，P2作为基本点，在剩余点中按照顺序选取一个点Px(x为剩余点中的一个)与基本点组成三角形。如图1所示，可以理解为三角形底边不变，顶点不断发生变化。在点集Q中选出的点为点集P中选取点的对应匹配点，同样操作，可以得到一个个对应的三角形。

图1 构造三角形

2.2三角形相似判断

判断两三角形相似的方法有3种，分别是：(1)三边对应成比例；(2)两个对应角相等；(3)一个对应角相等，对应角的邻边对应成比例。实际情况中，图像会有尺度、旋转等变化，在图像旋转过程中，三角形的角度变化会很大，所以选择三边对应成比例作为判断三角形相似的依据。图像经过变化，三角形不可能完全相似，因此需要设定一个允许的误差范围。经过实验，发现误差阈值κ设定在0.9的时候，能够在保证正确率的同时，保留很多的特征点。

三角形相似过滤流程如下：

第一步，取点集P中任意2个点P1,P2，与在剩余点中取一个点P3组成三角形，定义为△P1P2P3，那么点集Q中能有3个点Q1，Q2，Q3，与点集P中的P1,P2,P3为对应的匹配特征点，点Q1，Q2，Q3也组成一个三角形△Q1Q2Q3。

第二步，如果△P1P2P3∽△Q1Q2Q3，将P1,P2作为基础点，并将P3放入正确点集I中。继续从剩余点中取出变换点，与基础点判断相似，相似就为正确点，不相似就为误匹配点。基础点同样是正确点。如果△P1P2P3与△Q1Q2Q3不相似，那么把这3个点都作为变换点，在剩下的点中重新选取基础点和变换点，直到所取3个点与对应3个点组成的三角形相似。

第三步，将过滤过一次的所有正确点按照上述方法再过滤一遍。经过两次过滤后，剩下的匹配点就认为都是正确的匹配特征点。

2.3算法流程

图像经过构建尺度空间、特征点检测、特征点描述得到了特征点。经由欧氏距离相似性度量后得到匹配的特征点。此时的匹配点对中存在很多的错误匹配点，用三角形相似算法对匹配点进行过滤。经过这些步骤，得到了准确性更高的匹配点对。

3 实验结果及分析

为了验证本文算法对图像偏转以及图像放大缩小的适应性，下面分别对这两种情况进行验证。实验图像大小为1 024×768像素，由IMAGINGSOURCE相机采集。

第一组3幅实验图对图像的偏转进行了验证。图2(a)为原图，图2(b)为图2(a)偏转20°左右拍摄的图，图2(c)为图2(a)偏转40°左右拍摄的图。图3中的3幅图为经过RANSAC算法过滤的特征点匹配图，其中图3(a)为图2(a)与图2(b)特征点匹配图，图3(b)为图2(a)和图2(c)特征点匹配图。图4中的2幅图为经过本文三角形过滤的特征点匹配图，其中图4(a)为图2(a)与图2(b)特征点匹配图，图4(b)为图2(a)和图2(c)特征点匹配图。表1为图2(a)与图2(b)匹配结果比对，表2为图2(a)与图2(c)匹配结果比对。

图2 图像旋转配准

表1 图2(a)与图2(b)匹配结果

图3 旋转20°配准图像

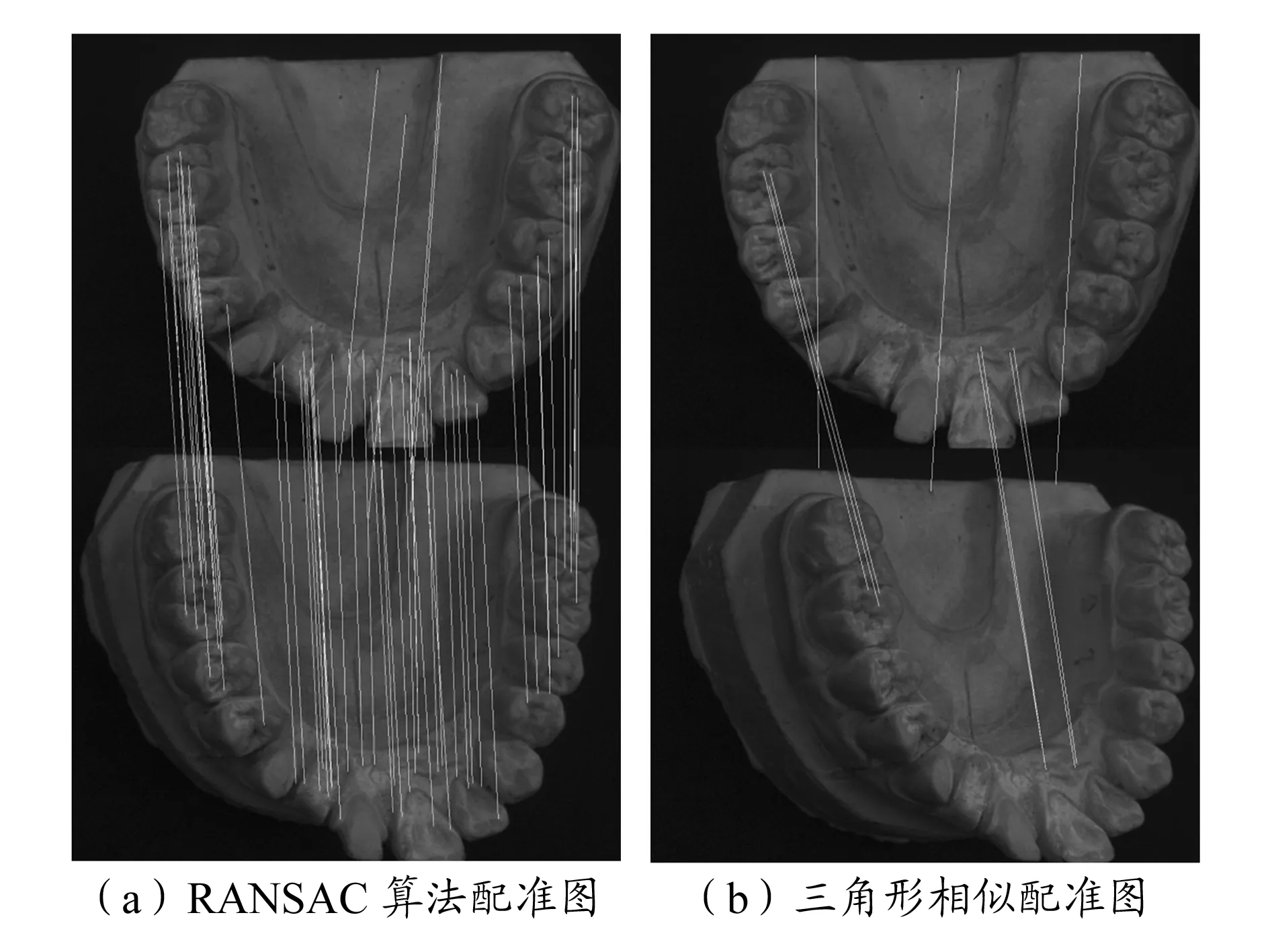
图4 旋转40°配准图像

表2 图2(a)与图2(c)匹配结果

在多次偏转图像实验中，经过三角形相似过滤的特征点的准确率能保持在98%以上。

第二组2幅实验图对图像的放大缩小进行了验证。图5(a)为原图，图5(b)为图5(a)放大图。图6所示为经过RANSAC算法过滤的特征点匹配图。图7所示为经过本文三角形过滤的特征点匹配图。表3为图5(a)与图5(b)匹配结果比对。

图5 图像大小变化

图6 RANSAC算法配准图 图7 三角形相似配准图

表3 图5(a)与图5(b)匹配结果

从实验结果来看，三角形过滤与RANSAC算法相比在正确率方面有比较大的优势，在运算时间上也有一定优势。只不过三角形过滤是在牺牲了很多正确点的情况下才保证了正确率，同时在特征点比较多的时候，三角形相似算法正确率也会有所下降。

4 结束语

文中所提算法是基于SIFT算法的一种改进过滤算法，该算法在SIFT算法用欧式距离判断相似性的基础上，用三角形相似对匹配点进行进一步过滤。实验结果表明，该算法在匹配特征点的准确率上有了很大提高，同时也缩短了匹配时间。但是该算法在过滤了错误匹配点的同时也过滤了很多正确的匹配点对，在今后的研究中，将努力改进此过滤算法，在保证准确率的同时，保留更多的正确匹配点。

[1] Mikolajczyk K，Tuytelaars T，Schmid C，et al．A comparison of affine region detectors[J]．International Journal of Computer Vision，2005，65(1/2)：43-72.

[2] Mikolajczyk K，Schmid C．A performance evaluation of local descriptors[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(10)：1615-1630.

[3] Foroosh H，Zerubia J B，Berthod Marc．Extension of phase correlation to sub pixel registration[J]．IEEE Transactions on Image Processing，2002，11(3)：188-200.

[4] 常青，张斌，邵金玲．基于SIFT和RANSAC的特征图像匹配方法[J]．华东理工大学学报：自然科学版，2012，38(6)：747-751.

[5] 刘焕敏，王华，段慧芬．一种改进的SIFT双向匹配算法[J]．兵工自动化，2009，28(6)：89-91.

[6] 霍春雷，周志鑫，刘青山，等．基于SIFT特征和广义紧互对原型对距离的遥感图像配准方法[J]．遥感技术与应用，2007，22(4)：524-530.

[7] 张锐娟，张建奇，杨翠，等．基于CSIFT的彩色图像配准技术研究[J]．光学学报，2008，28(11)：2097-2103.

[8] 袁杰．基于SIFT的图像配准与拼接技术研究[D]．南京：南京理工大学，2013.

[9] 吴慧兰，刘国栋，刘炳国，等．基于SIFT算法的圆心快速精确定位技术研究[J]．光电子·激光，2008，19(11)：1512-1515.

[10] Lowe D G．Distinctive image features from scale-invariant keypoints[J]．International Journal of Computer Vision，2004，60(2)：91-110.

ANewAlgorithmforFilteringSIFTFeatureMatching

JIANG Zhongjie, CHENG Xiaosheng, CUI Haihua, ZHANG Yihua

(Nanjing University of Aeronautics & Astronautics, Jiangsu Nanjing, 210016, China)

It proposes a SIFT matching algorithm presence of mismatch based on triangle similarity matching feature points filtering algorithms. This algorithm uses the feature points in the Euclidean distance to determine the similarity of the SIFT algorithm for matching feature points structure triangle, discriminates the feature points further filtration to realize the triangle similarity matching. The experimental results show that the algorithm is similar to the triangle, and greatly improves the matching accuracy.

Image Mosaic; SIFT Algorithm; Triangle Similarity; Match Point Filter

10.3969/j.issn.2095-509X.2014.09.010

2014-08-09

国家863计划资助项目(SS2013AA040802)；江苏省博士后科学基金资助项目(1301104C)；江苏省数字化制造技术重点实验室开放基金资助项目(HGDML-1103)；南京市产学研项目(201306007)

蒋中杰(1989—)，男，江苏江阴人，南京航空航天大学硕士研究生，主要从事为图像处理、图像拼接等方面的研究。

TP751

A

2095-509X(2014)09-0040-04