一种基于累积误差优化分配的多视角拼接方法

汤明辉，程筱胜，崔海华，戴 宁

(南京航空航天大学 机电学院，江苏 南京 210016)

一种基于累积误差优化分配的多视角拼接方法

汤明辉，程筱胜，崔海华，戴 宁

(南京航空航天大学 机电学院，江苏 南京 210016)

多视角三维拼接是三维测量的重要组成部分，为了提高多视角拼接的精度，提出了一种基于累积误差优化分配的多视角拼接方法。根据多视角点云数据的空间位置信息，构建环形拼接生成树，利用设计的环形结构将拼接产生的累积误差分散到各个视角，从而逐步提高整体拼接精度。实验表明，该方法能获得令人满意的拼接精度。

多视角拼接；生成树；误差分配；累积误差

非接触式测量是由光学设备获取物体表面图像，进行处理后获得物体表面的三维数据。计算机技术以及光电技术的结合促进了非接触式测量技术的发展和应用。然而受限于光学设备的视场，在实际测量过程中，单视角的测量并不能获取物体完整的表面信息，因此需要将多视角测量的数据进行拼接。寻找点云或者网格数据之间的位置变换关系，将多片点云或者网格数据统一到唯一的全局坐标系下，称为三维点云配准，在不同场合也被称为重定位或者三维点云拼接。

多视角拼接中最基础、最简单的情况是两视角的点云拼接，对两视角的点云或网格数据拼接，国内外研究成果众多。无点云初始位置信息的拼接，称为粗拼接，需建立三维特征进行匹配，从而获取点云中配对的点对，通过计算获得点云片间的初始位置。可利用的三维特征一般有点签名[1]、Spin图像[2]等。基于三维特征的无初始位置拼接往往不能获得精确位置，仍然需要调整点云的相对位置。对于点云的初始位置已知的两视角点云拼接，称为精拼接。迭代最近点[3]算法及其相关改进算法[4]是目前应用最广泛的无特征精拼接方法。迭代最近点算法是将另一片点云中最近的点作为一个匹配点，获得大量的匹配点后计算点云的位置，然后再选择最近点，如此反复循环迭代直至满足算法结束的条件(最近点距离小于一定阈值或者迭代达到一定次数)。

对多视角点云，若将点云依照两两拼接的方式进行拼接，微小的误差会逐渐累积，累积误差会使点云位置错位。相对于两视角点云拼接，如何将多视角拼接的累积误差合理地分配到各视角点云数据上，是一个亟需解决的问题。Kari[5]将计算点云间重叠区域所得的百分比，确定为点云之间拼接的可靠性系数，重叠区域大的，确定为优先拼接的对象，逐步将所有的点云拼接到一处，从而分配累积误差。YangChen[6]等人则将拼接完成的点云进行融合，未拼接的点云依次拼接到融合完成的点云上，再次融合，如此反复，直至拼接完成，该方法分配累积误差的方法并不均匀。Sharp[7]等人则将累积的误差均匀分配到各点云中，并未考虑不同点云间大小不同的重叠区域对误差分配的影响。也有一些学者另辟蹊径，如Takeshi Masuda[8]利用空间中的采样点建立有向距离场(Signed Distnce Field， SDF)来调整各点云之间的相对位置，在采样点足够密集，而且点云的起伏变化并不剧烈时，该方法可以获得良好的拼接效果，该方法的另一优势在于可以同时调整所有视角的点云姿态。

本文提出了一种多视角点云数据拼接的新方法，拼接构成的累积误差根据点云间的重叠区域的大小来分配，相较于均匀分配的方式，该方法更为可靠合理。该方法采用生成树来表示点云之间的拓扑关系，从而避免了穷举所有的点云组合关系来进行拼接，大大减少所需计算的组合数量，减少了计算量，提高了计算效率。

1 多视角拼接方法

1.1生成树的构建

传统的方法有将任意两片点云进行拼接的方法，此方法需要遍历所有的两两点云组合，计算量甚大，盲目性过大，如图1所示，对于有N个视角的点云数据需要进行N×(N-1)次计算，同时该方法也存在不合理的地方，单纯只考虑了两片点云间的关系，没有考虑到多视角点云间复杂的相互关系，故所得的拼接结果精度有限。

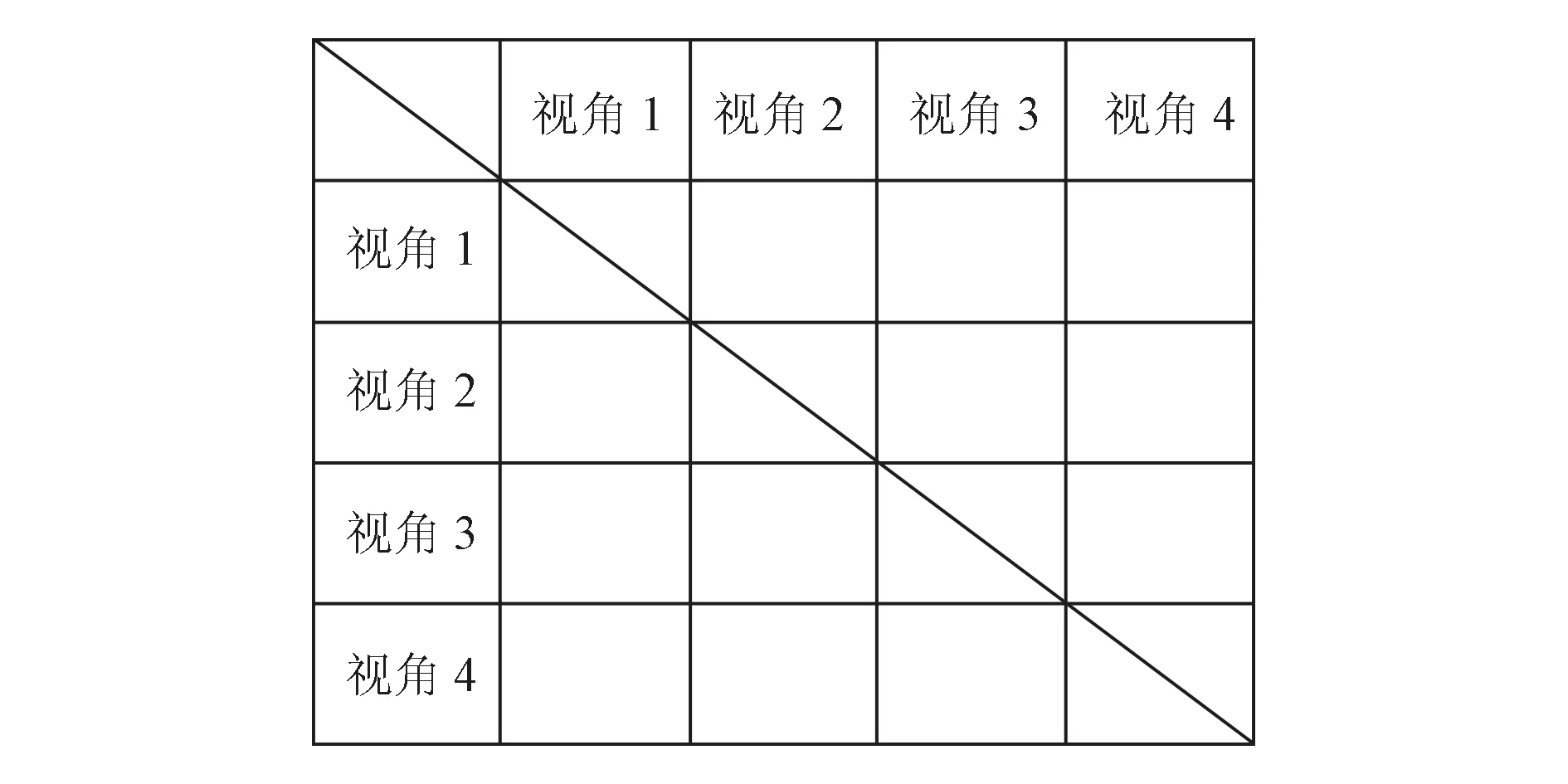
图1 两两拼接多视角拼接组合示意图

对一个完整的物体进行扫描，多视角点云数据会构成一个封闭的整体，这些不同视角的点云数据可以拆分成最基本的环形结构，即多片点云构成一个首尾相接的环形。无论多复杂的点云关系，都可以拆分成一系列的环形结构，如图2所示，其中连接不同视角的直线表示这两个视角之间存在重叠区域。

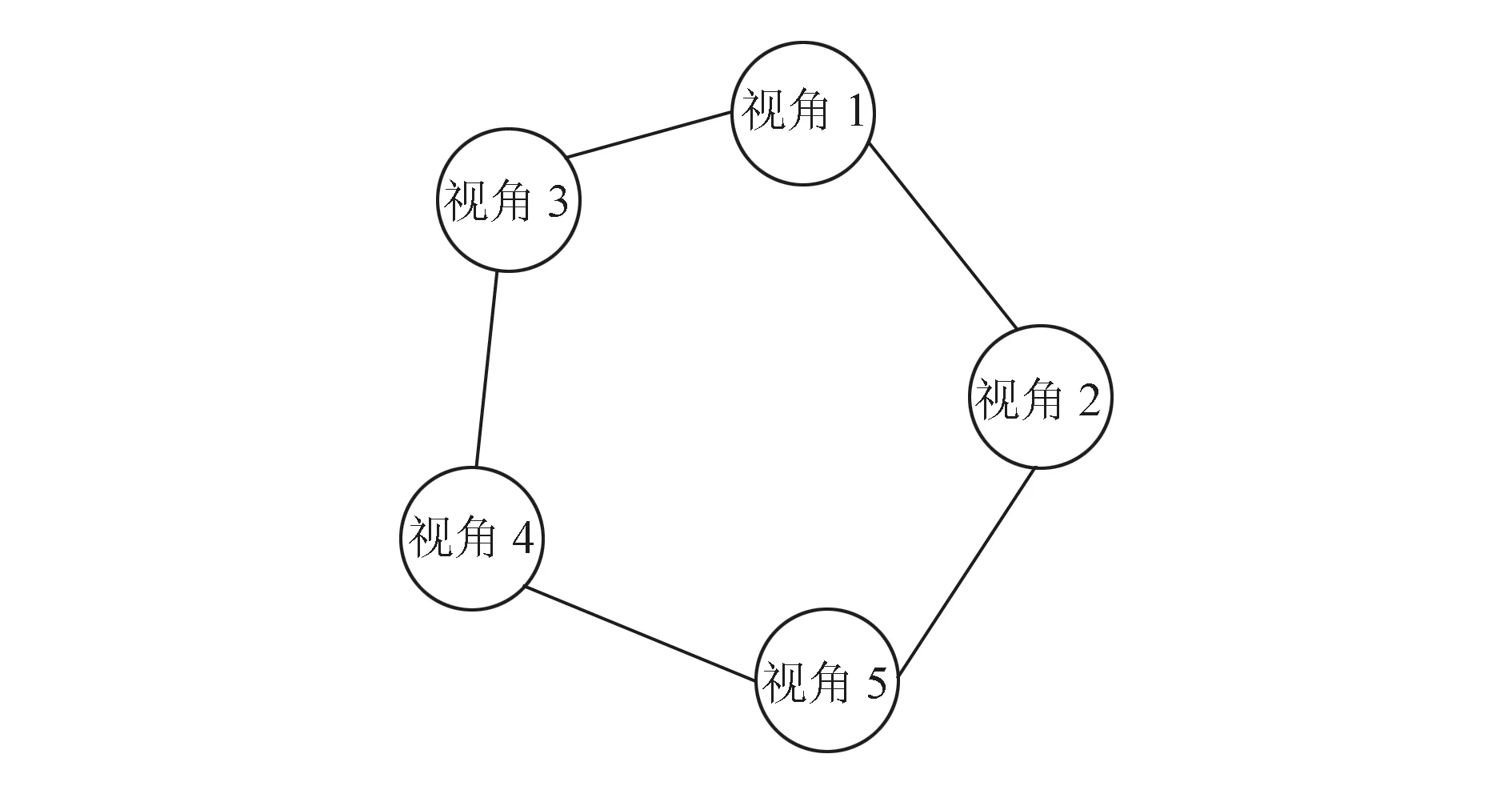
图2 多视角点云相互关系示意图

在对多视角点云进行拼接之前，首先需要确定各视角点云之间的关系，比较简单的方法是检测各点云的包围盒是否相交，从而快速判断不同视角点云之间是否存在相交区域。另一种较为精确的方法是对点云进行降采样后，利用kd树[9]等搜索在另一片点云上是否存在距离小于指定阈值的点，若存在则认为有重叠，该方法的优势在于当采样点足够多时可以将有匹配点的采样点数量除以总的采样点数量，大致估算出两片点云的重叠区域大小。

构成环形的视角数量并不恒定，因此需要有合适的方法将所有的环形结构筛选出来，此处引入图论中生成树的概念，基于之前对于点云是否存在相交区域的判断结果，构建生成树(Spanning Tree)[10]。下面以5个视角的点云数据为例介绍生成树的一些特性，5个视角的点云数据抽象为5个点，用线连接的2个点表示这2个视角的点云数据存在重叠部分，如图3所示。

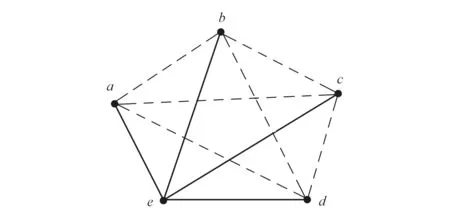
图3 5点构成的生成树

生成树的一个特点在于将树上的任意两个端点连接起来即可构成一个环形结构，如图3所示，将a,c相连，a-e-c-a构成一个环形；将a,d相连，a-e-d-a构成一个环形，依此类推，可以穷举多视角点云数据构成的环形结构。在实际应用中，并不是所有的点云之间都存在相交区域，可以根据这些关系来去除部分不存在的环形结构，减少计算量。

1.2环形结构多视角点云拼接

1.2.1环形结构拼接问题

由1.1节可以知道，利用生成树可以将多视角点云数据划分为基础的环形结构，本节将讨论环形结构的多视角点云数据拼接。如图4所示，对环形结构的存储罐模型采集点云数据，利用迭代最近点算法将点云两两拼接，可以明显发现：由于累积误差的存在，最后一片数据和第一片数据之间的重叠区域偏差距离远大于0.145mm(图4(b)中椭圆框选区域)，而且拼接效果良好的区域可以观察到两片点云相互交错，图4中并没有观察到该现象。

点云间重叠区域更大的两片点云拼接结果相较于重叠区域较小的两片点云，其拼接结果更为可靠，因此考虑到不同视角点云的重叠部分不同，将累积误差平均分配给环形结构中各视角点云是不合适的——被移动的点云应该更靠近重叠部分较大的作为参照基准的另一部分点云。运用迭代最近点算法进行拼接时，为了提高运算效率，对点云进行随机采样后搜索匹配点，重叠区域更大的点云之间，匹配点的数量更多，点云会被“拉近”重叠区域更多的点云，利用这一特性，可以将累积误差分配到构成环形结构的各视角的点云数据中去。

图4 6视角点云数据两两视角拼接累积误差示意图

实际测量过程中获得的多视角点云数据的拓扑信息往往比较复杂，如图5所示，V1和V2，V2和V3进行拼接，由于进行的是两两拼接，V1视角和V3视角存在的重叠部分对拼接结果并没有影响，因此更容易造成误差的累积。

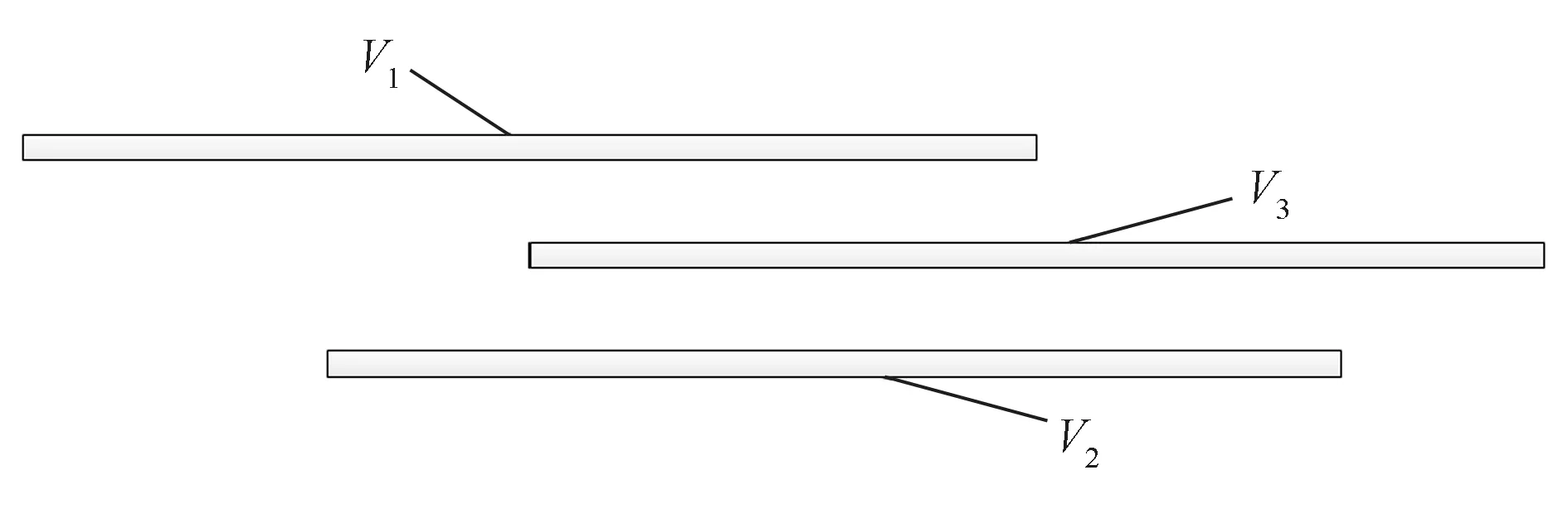
图5 3视角点云示意图

1.2.2用于环形结构拼接的金字塔模型

考虑到上述问题的存在，本文基于迭代最近点算法提出了一种新的误差分配方法，称为金字塔模型，根据点云间的重叠率来分配多视角环形结构拼接产生的累积误差。

下面以4个视角点云数据的环形结构拼接为例，详细说明使用金字塔模型进行拼接的方法。4个视角采用V1，V2，V3和V4表示，4视角之间存在的重叠区域如图6所示，图中的连接线表示两视角之间存在重叠区域，为简化模型，假设每个视角只与其相邻的视角存在重叠区域。

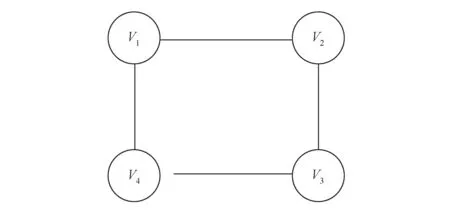
图6 4视角环形结构

如图7所示，将视角V1算作两个视角，打开环形结构的链条，构建金字塔模型的第1层。

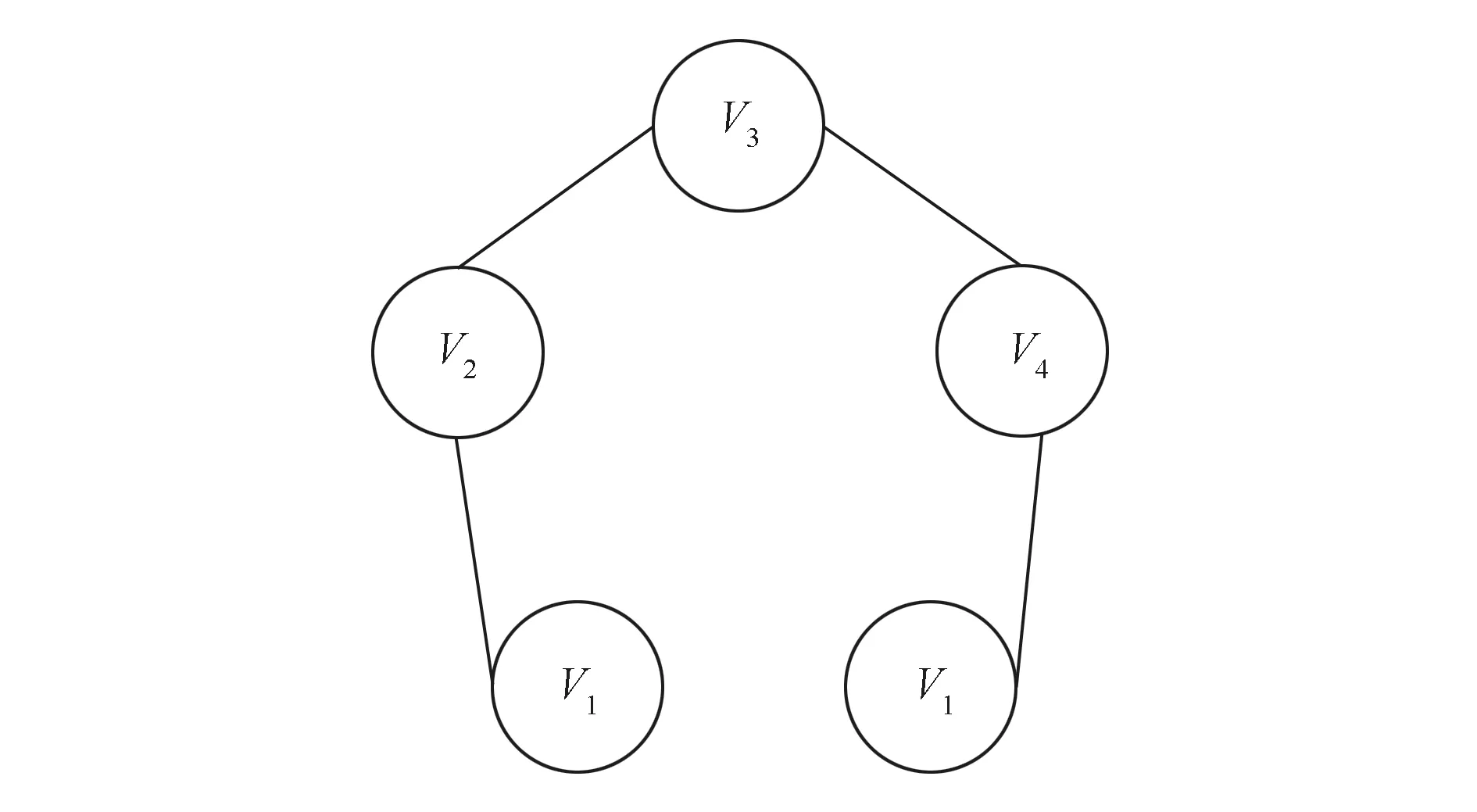
图7 4视角环形结构的打开

利用迭代最近点算法，调整相邻两视角的位置，即以V1为基准，将V2拼接到V1上去，拼接完成后，将V3拼接到V2上去，依此类推，最后将另一片V1拼接到V4上，自此完成金字塔模型第2层的构建，如图8所示。

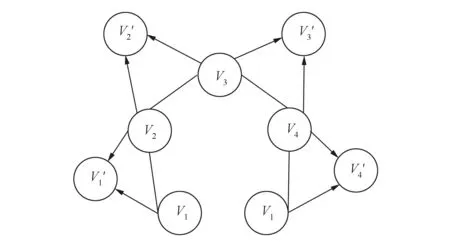
图8 金字塔模型第二层的构建

仿照金字塔模型第2层的构建，构建第3层的视角V1″，V2″和V3″，再构建第4层的视角V1‴和V2‴，最终生成拼接参考模型V。金字塔模型各层各视角间关系如图9所示。

将视角V1视作两个视角打断环形结构之后，可以发现倒数第2层的两个视角V1‴和V2‴中均含有视角V1的点云数据，其中V1‴包含视角V1，V2，V3和V4的数据，而V2‴则包含V2，V3，V4和V1的数据，视角V1的数据会将两个视角V1‴和V2‴相互拉近，两个视角V1‴和V2‴中包含的视角V2，V3和V4的数据相互分开，从而将累积的误差分配到各点云中去，以生成的金字塔模型为基准，将V1，V2，V3和V4拼接到金字塔模型V上去，完成环形结构多视角点云数据的拼接。

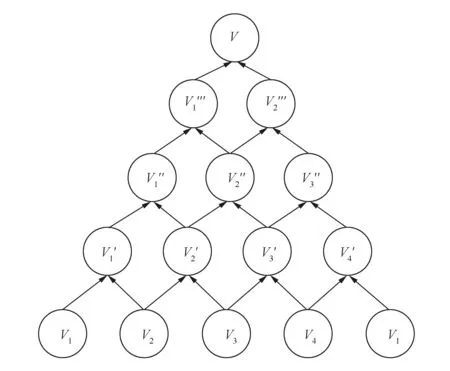
图9 金字塔模型示意图

2 实验结果

为减少数据量，对点云数据进行采样后选取匹配点进行拼接(不建议直接对点云进行降采样后使用降采样的点云进行拼接，这样虽然减少了数据量，但是大量原先处于相同位置点的存在会导致点云的“锁死”，难以获得良好的结果，因此本文在进行实验时存储各视角点云数据的旋转平移关系，即4×4的旋转平移矩阵)。金字塔模型中每片点云生成时，都进行随机采样，获得不同的点构成新的点云数据，而采样后获得的点在寻找匹配点时，可以根据存储的旋转平移矩阵转换到匹配点所在视角的坐标系下，获得尽可能可靠的匹配点，从而提高点云拼接的精度。由于拼接时点云受到的“拉力”取决于点的数量，故为了将累积误差合理分配，需保持视角V1采样的数据量与剩余视角的总数据量相同。对石膏制存储罐模型进行扫描重建，获得6个不同视角下的三维点云数据，6视角的数据为环形结构，多视角点云依靠扫描仪的机械转台进行粗定位。多视角点云数据拼接前后的位置以及精度分析如图10所示。

从图10可以看到，各视角点云数据在拼接之后重叠部分有良好的交错区域，利用Gemagic Studio 12软件分析可发现重叠部分的平均距离在0.028mm以下。

图10 储蓄罐6视角点云拼接

对石膏牙模采集数据，依照本文方法进行拼接，数据分析结果如图11所示。

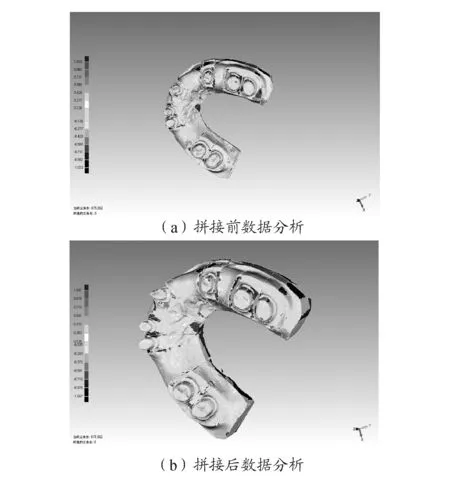
图11 石膏牙模多视角点云拼接

由图11可以看到各视角点云重叠部分的平均距离由拼接前的0.126mm下降到0.035mm，Gemagic全局注册功能拼接结果则为0.033mm。

对石膏储蓄罐模型和石膏牙齿模型测量后进行拼接，部分实验数据见表1。

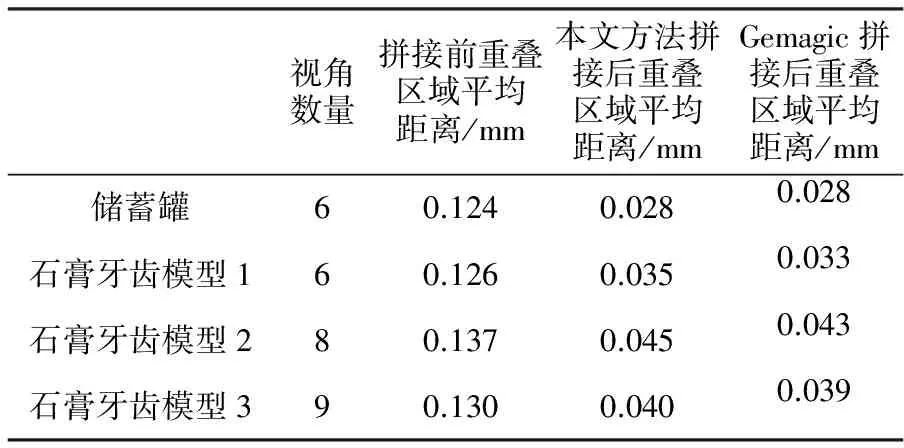
表1 实验结果

3 结束语

本文提出了一种新的多视角拼接方法，利用多视角点云之间的位置关系，基于生成树构建环形结构，合理有效地分配了环形结构中由拼接造成的累积误差。实验表明，该方法能获得令人满意的拼接结果，相较于以往的拼接方法，误差分配更平均合理。然而在视角数量较多时，由于生成了大量的环形结构，会导致算法运行需要较多的时间，如何提高算法效率是后续研究需要解决的问题。

[1] Chua C S, Jarvis R. Point signatures:a new representation for 3d object recognition[J]. International Journal of Computer Vision, 1997, 25(1): 63-85.

[2] Johnson A E, Hebert M. Using spin images for efficient object recognition in cluttered 3D scenes[J].Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1999, 21(5): 433-449.

[3] Besl P J, McKay N D. Method for registration of 3-D shapes[C]//Robotics-DL tentative. International Society for Optics and Photonics, 1992: 586-606.

[4] Rusinkiewicz S, Levoy M. Efficient variants of the ICP algorithm[C]//3-D Digital Imaging and Modeling, 2001. Proceedings. Third International Conference on. IEEE, 2001: 145-152.

[5] Pulli K. Multiview registration for large data sets[C]//3-D Digital Imaging and Modeling, 1999. Proceedings. Second International Conference on. IEEE, 1999: 160-168.

[6] Chen Y, Medioni G. Object modelling by registration of multiple range images[J]. Image and Vision Computing, 1992, 10(3): 145-155.

[7] Sharp G C, Lee S W, Wehe D K. Multiview registration of 3D scenes by minimizing error between coordinate frames[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2004, 26(8): 1037-1050.

[8] Masuda T. Registration and integration of multiple range images by matching signed distance fields for object shape modeling[J]. Computer Vision and Image Understanding, 2002, 87(1): 51-65.

[9] Liu T, Moore A W, Yang K, et al. An investigation of practical approximate nearest neighbor algorithms[C]//Advances in Neural Information Processing Systems,2004: 825-832.

[10] Rosen R. The theory of graphs and its applications[J]. Bulletin of Mathematical Biology, 1962, 24(4): 441-443.

Multi-viewRegistrationof3DScenesBasedonAllocatingCumulativeErrors

TANG Minghui, CHEN Xiaosheng, CUI Haihua, DAI Ning

(Nanjing University of Aeronautics & Astronautics, Jiangsu Nanjing, 210016, China)

Multi-view three-dimensional registration is an important part of three-dimensional measurements. In order to improve the accuracies of multi-view registration, it proposes a method based on optimal allocation of cumulative errors. According to the spatial position information of multi-view point cloud data, this method constructs a ring based on spanning tree, distributes the accumulated errors to each perspective. This can gradually improve the overall accuracies. Experiments show that the method can obtain satisfactory registration precision almost reached with the same effect of those commercial softwares.

Multi-view Registration; Spanning Tree; Error Allocation; Cumulative Errors

10.3969/j.issn.2095-509X.2014.09.005

2014-08-19

国家863计划资助项目(SS2013AA040802)；国家自然科学基金资助项目(51305201)；江苏省精密与微细制造技术重点实验开放基金；南京市产学研项目(201306007)

汤明辉(1990—)，男，江苏南京人，南京航空航天大学硕士研究生，主要研究方向为图像处理、非接触三维几何测量、三维拼接。

TP399

A

2095-509X(2014)09-0018-05