排爆机器人五自由度操作臂动力学分析
明 添,钱瑞明
(东南大学 机械工程学院,江苏 南京 211189)
排爆机器人五自由度操作臂动力学分析
明 添,钱瑞明
(东南大学 机械工程学院,江苏 南京 211189)
结合排爆机器人的研制,针对安装于排爆机器人移动平台上的五自由度操作臂实际结构,首先测算出操作臂的惯性参数,并由此建立动力学模型,推导出拉格朗日动力学方程和参数;然后模拟排爆抓取任务,规划了操作臂各关节三段式五阶多项式运动规律,由动力学方程仿真求得各关节电机的力矩变化规律,并结合电机性能参数验证了运动规划的合理性。
排爆机器人;操作臂;动力学建模;运动规划;动力学分析
排爆机器人可以代替人到危险环境中进行排除危险物作业[1],在世界范围内,排爆机器人已经成为反恐作战的重要装备之一。排爆机器人通常由移动平台和操作臂组成,其中移动平台的行走能力决定了机器人可达区域,操作臂的运动学、动力学特性决定了排爆作业能力。本文结合排爆机器人研制项目,基于拉格朗日法研究安装于移动平台上的操作臂的动力学特性。
多自由度操作臂动力学分析的关键是获取与实际结构相符的动力学惯性参数。由于操作臂涉及的零部件很多,且形状各异,为简化计算,目前多数文献会选择简化杆臂模型并忽略驱动机构惯量(如将臂杆简化为纯圆柱体[2]或纯长方体[3]),由此计算出的结果与实际情况存在较大的偏差,难以应用至实际控制与机构改进。本文对操作臂结构不作任何简化与假设,通过软件测算获得动力学计算中所需的参数,由此可大大提高动力学分析的准确性。通过模拟实际排爆任务制定运动规划和求解相应的动力学方程,获得各关节力矩的变化规律,并结合驱动电机的转速、扭矩特性进行验证,由此为控制系统和算法的设计提供依据。
1 操作臂结构及位姿描述
本文所研究的操作臂搭载于排爆机器人移动平台上,共有6个自由度(包括1个夹持器张合自由度),可到达空间任意位置,并满足常规排爆抓取作业姿态需要,机构中存在1个冗余自由度,可以使操作臂具有一定的避障抓取能力。外形如图1所示。
图1 操作臂外形图
操作臂各杆上建立的坐标系如图2所示,相邻坐标系之间的变换参数见表1。
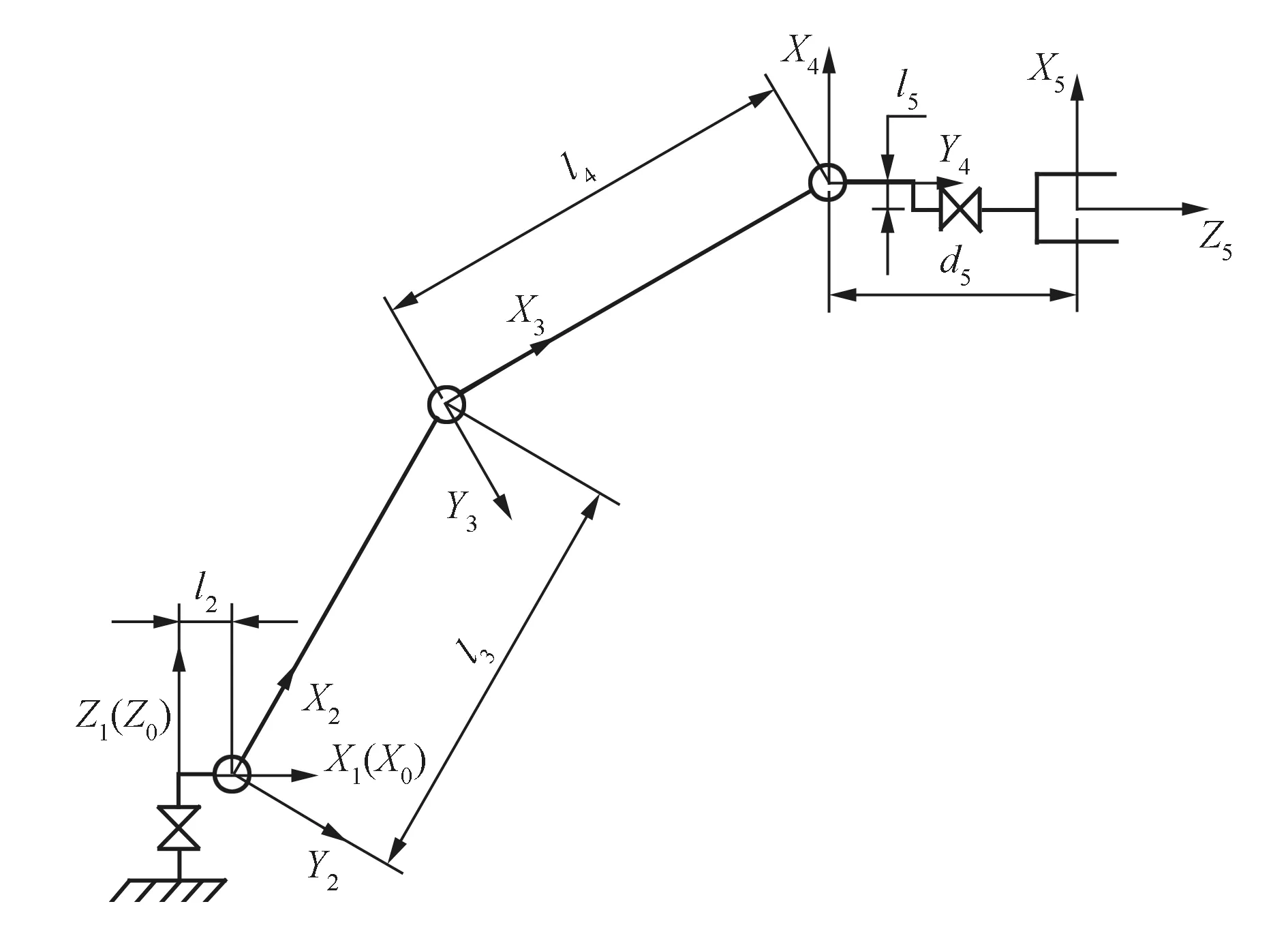
图2 操作臂机构示意图与坐标系设置

表1 各杆臂参数
相邻坐标系的位姿变换矩阵如下:

其中:si=sinθi,ci=cosθi,i=1,2,…,5。
2 操作臂动力学模型的建立
2.1操作臂拉格朗日动力学方程
由文献[4]可得操作臂的拉格朗日动力学方程为
式中:Dij为加速度惯量;Dijk为科里奥利力和向心力;Di为重力;Iai为驱动机构惯量。
由文献[5]可得Dij=Dji,Dijk=Dikj,关节扭矩方程推导如下:
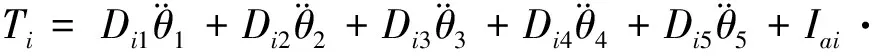
2.2动力学方程参数
由操作臂动力学方程可知,若求各个关节扭矩,则需求得参数Dij,Dijk,Di和Iai,为此必须求得各个杆臂的质量mi、质心ri、伪惯性矩阵Ji,并测算出传动装置惯量Iai。为了得到准确的数据,本文将操作臂拆分为5个杆臂,并由三维软件测算各个杆臂的质量、质心以及转动惯量,得到的参数见表2。
Iai可按下式计算[5]:
式中:Jm为伺服电机的转子转动惯量;J1,J2为第一、二级减速器的转动惯量;I为总传动比,i1,i2为第一、二级减速器的传动比。
本操作臂各关节使用的是MAXON伺服电机集成的第一级减速器,转动惯量可在MAXON产品手册中查到;关节2,3使用了APEX第二级减速器,可从产品手册中查取转动惯量,剩余第二级减速器转动惯量通过SolidWorks软件进行测算,参数汇总见表3。
3 操作臂动力学仿真
3.1任务制定
设定操作臂处于初始位姿,在基坐标空间内有一疑似爆炸物,首先通过视觉系统获取疑似爆炸物的位姿信息,在机器人内部生成目标位姿矩阵,然后通过操作臂各关节的运动实现对爆炸物的抓取。现对操作臂从初始位姿到目标位姿这一过程进行关节运动规划和动力学分析。
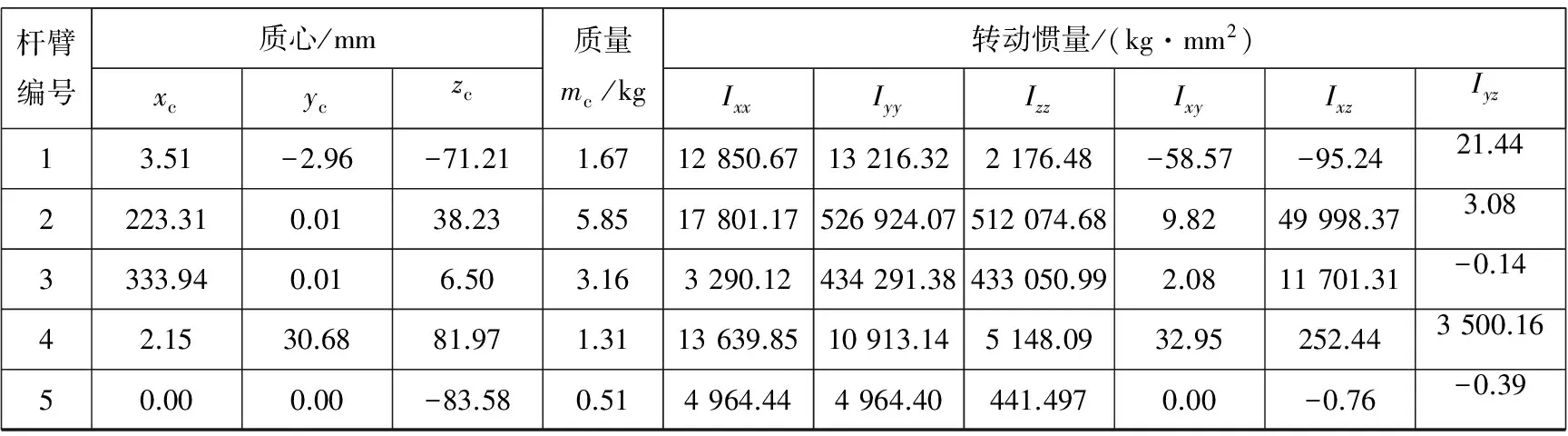
表2 各杆臂参数
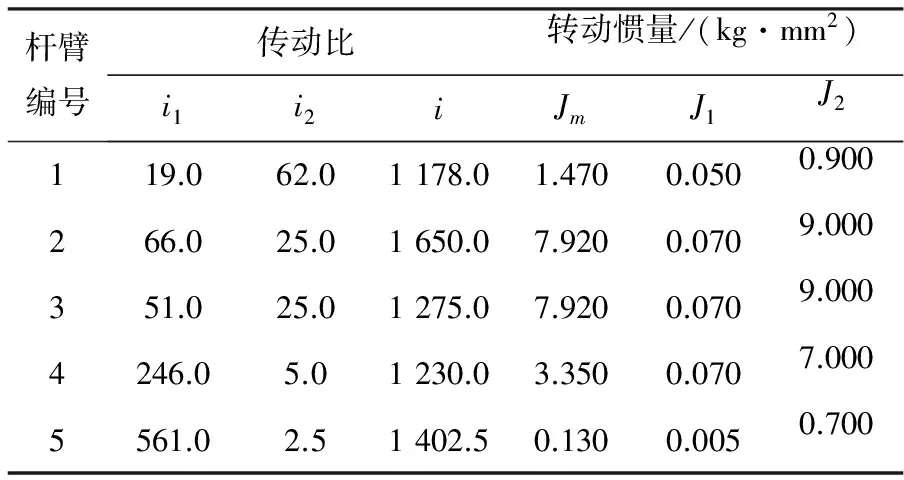
表3 驱动机构传动比与转动惯量
操作臂初始位置位姿矩阵为:
设由视觉系统获得的目标位姿矩阵为:

3.2操作臂运动规划
为保证运动的平稳性,将运动过程分为3段:
a.PA~PB,靠近目标位置,末端坐标系姿态保持不变;
b.PB~PC,将末端坐标系移动至目标正上方,并调整使其到达目标姿态,夹持器张开;
c.PC~PD,末端坐标系下移至目标位置,姿态不变,夹持器闭合,完成抓取。
其中,
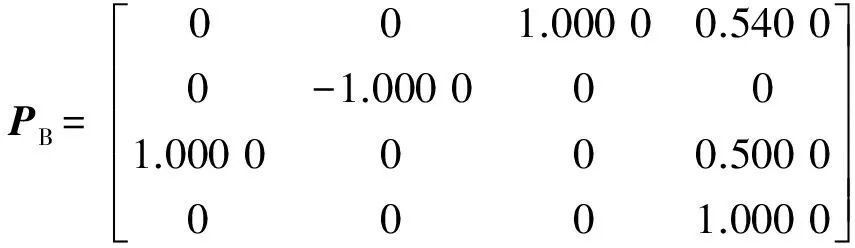
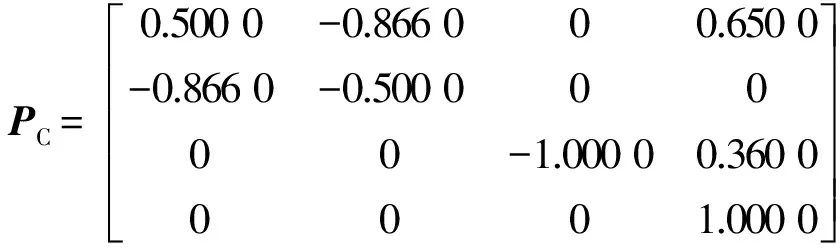
逆运动学求解对应各点关节角度:
θA=[0° -180° 162° -72° 0°]T
θB=[0° -108.4° 97.3° -78.9° 0°]T
θC=[0° -59° 34.4° 24.6° 60°]T
θD=[0° -62.8° 78.1° -15.3° 60°]T
现对关节空间进行运动规划,并采用五阶多项式作为路径段,设定PA~PB历经4s,PB~PC历经4s,PC~PD历经2s。由此,可以求得3个阶段的关节角位移、角速度和角加速度的变化曲线图,整合后如图3、图4、图5所示。从图3可以看出,各关节角的位移均在表1指定的范围内,符合要求。
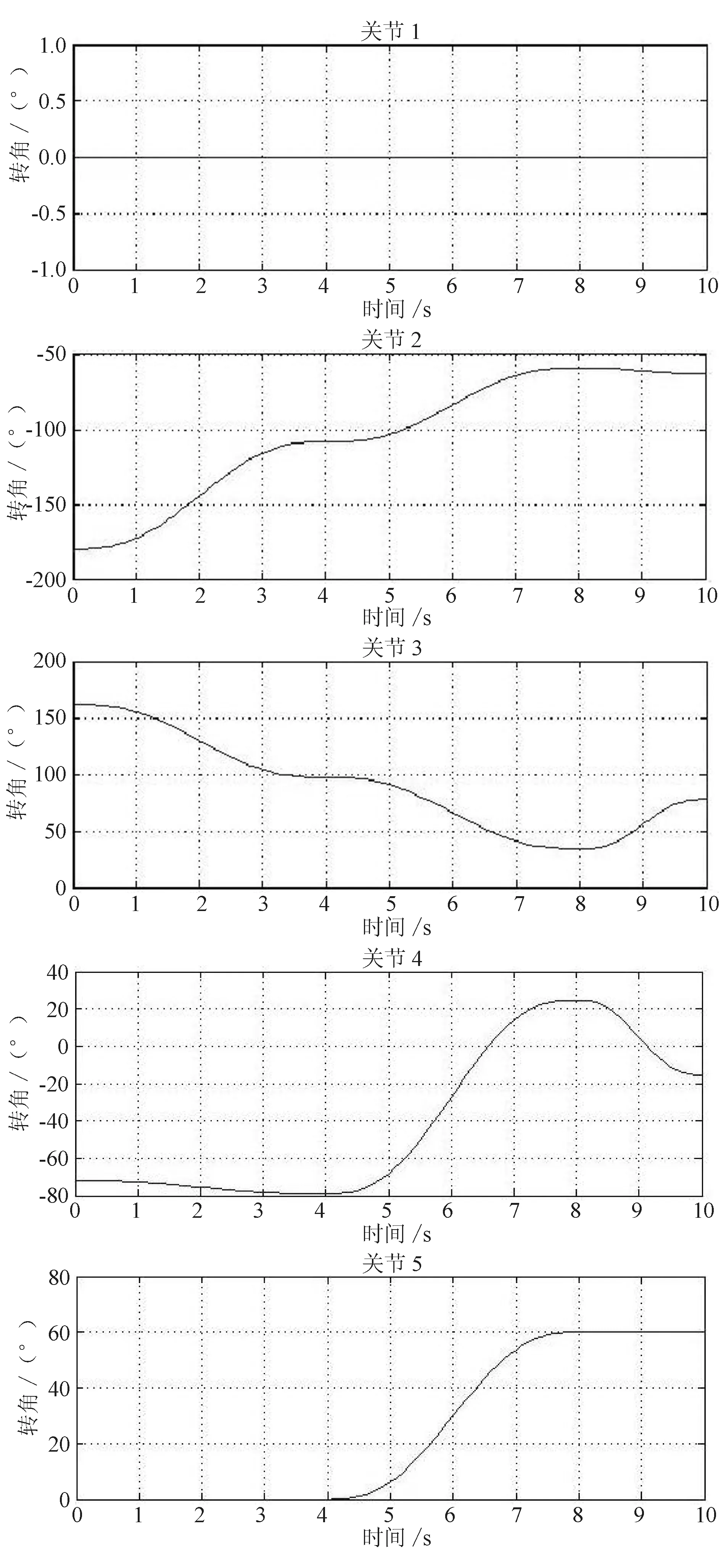
图3 操作臂各关节角位移变化曲线
3.3仿真结果
运用MATLAB软件的动力学计算程序,将关节运动方程带入动力学方程中计算,可得到各关节的力矩变化曲线图,如图6所示。从图中可以看出,关节1未转动,电机扭矩只受到其他关节的加速度惯量、科里奥利力和向心力的影响,变化相对较小;关节2电机扭矩变化较大,对比此关节的角加速度变化曲线与电机扭矩变化曲线,以及重力项变化曲线可得,影响扭矩的主要因素是操作臂自重与关节角加速度;关节3、关节4、关节5的角加速度变化曲线与关节电机扭矩变化曲线有明显的拟合性,可以判断本运动规划中关节角加速度对以上3个关节的电机扭矩影响较大。
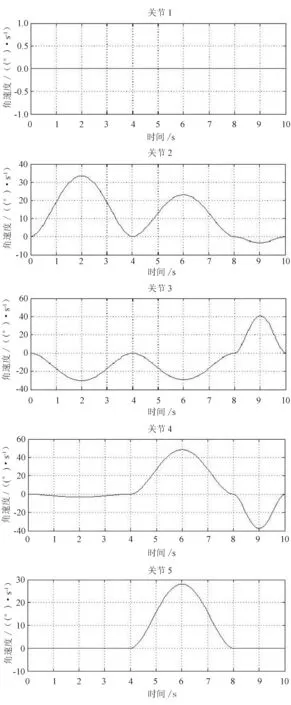
图4 操作臂各关节角速度变化曲线
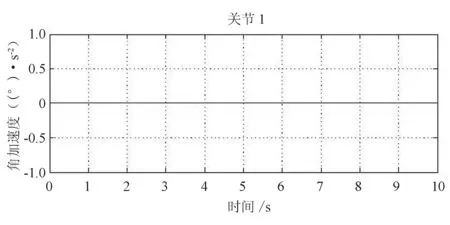
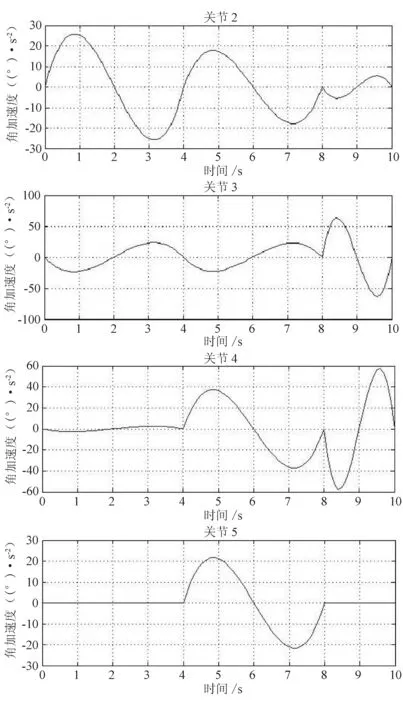
图5 操作臂各关节角加速度变化曲线
综上所述,关节力矩主要受杆臂重力和关节角加速度影响,关节角速度产生的影响较小,某些时候可以忽略不计。
3.4轨迹规划合理性验证
关节运动规划的合理性需要结合驱动电机的转速、扭矩特性进行验证。参考MAXON产品目录(2013/14),获取各个关节电机的运行范围图,判断各个关节电机在仿真过程中的转速与扭矩是否落在连续运行范围内。
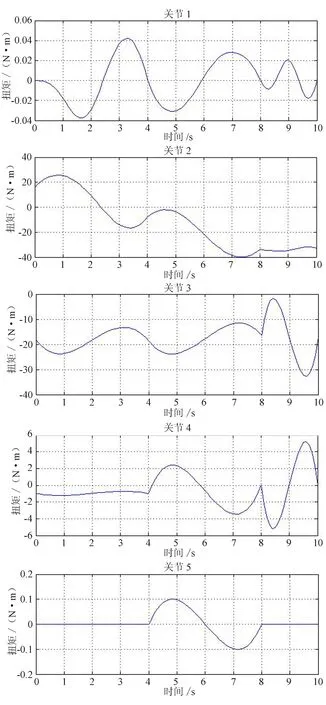
图6 操作臂各关节电机扭矩变化曲线
经计算,关节1~5电机的最大转速与扭矩如下:(1)转速峰值为0r/min,扭矩峰值为0.063 7mN·m;(2)转速峰值为9 228.5r/min,扭矩峰值为37.6mN·m;(3)转速峰值为8 705.4r/min,扭矩峰值为39.5mN·m;(4)转速峰值为9 950.9r/min,扭矩峰值为7.85mN·m;(5)转速峰值为6 574.6r/min,扭矩峰值为0.12mN·m。所有关节均在连续运行范围内工作,符合电机性能参数要求。
4 结束语
本文针对排爆机器人的操作臂进行了拉格朗日动力学建模,并通过模拟作业运动规划进行了基于MATLAB的动力学仿真,最后结合电机的性能参数验证了运动规划的合理性。从控制的角度来看,可以通过控制输入电压来调整转速-扭矩曲线在特性曲线图上的位置,通过控制电流来调整电机的输出扭矩,这样就可以通过控制电压和电流来控制电机的输出转速与扭矩,结合操作臂的运动方程和动力学方程,可实现操作臂基于动力学的运动控制。
[1] 李科杰. 危险作业机器人发展战略研究[J].机器人技术与应用,2003(5): 14-22.
[2] 陈辛. 机械臂动力学研究[D]. 哈尔滨:哈尔滨工程大学,2007.
[3] 万海波. 五自由度机械手的运动学和动力学分析[D]. 天津:河北工业大学,2006.
[4] John J Craig. 机器人学导论[M]. 北京:机械工业出版社,2006.
[5] LI Wei, YANG Yi, SHENG Deren, et al. Nonlinear dynamic analysis of a rotor/bearing/seal system[J]. Journal of Zhejiang University:SCIENCE A (Applied Physics &Engineering),2011,12(1): 46-55.
DynamicAnalysisofFive-DOFManipulatorofExplosiveDisposalRobot
MING Tian, QIAN Ruiming
(Southeast University, Jiangsu Nanjing, 211189, China)
Based on the development of explosive disposal robot and the real structure of five-degree of freedom manipulator assembled on the mobile platform, it measures and calculates the inertial parameters of the manipulator, establishes the dynamic model and Lagrange dynamic equation. Based on the simulation of the grasping mission, it plans the five order polynomial motion laws for the five joints, and illustrates the torques of each joint through dynamic equation. Combined with performance parameters of motors, it demonstrates the rationality of motion laws.
Explosive Disposal Robot; Manipulator; Dynamic Model; Motion Planning; Dynamic Analysis
10.3969/j.issn.2095-509X.2014.09.004
2014-08-18
明添(1990—),男,山东济宁人,东南大学硕士研究生,主要研究方向为机器人学。
TH113.2
A
2095-509X(2014)09-0013-05

