基于矩阵分解的四关节机械手运动学逆解研究

李小霞，汪木兰，殷红梅，许云飞

(1．江苏食品药品职业技术学院 机电工程系，江苏 淮安 223003)(2．南京工程学院 先进数控技术江苏省高校重点建设实验室，江苏 南京 211167)(3．淮安信息职业技术学院 机电工程系，江苏 淮安 223003)

基于矩阵分解的四关节机械手运动学逆解研究

李小霞1，汪木兰2，殷红梅3，许云飞1

(1．江苏食品药品职业技术学院 机电工程系，江苏 淮安 223003)(2．南京工程学院 先进数控技术江苏省高校重点建设实验室，江苏 南京 211167)(3．淮安信息职业技术学院 机电工程系，江苏 淮安 223003)

以自主研发的NGR01型四关节机械手为研究对象，基于机械手运动学方程，提出一种实时高精度逆运动学算法。该算法首先通过符号运算将矩阵方程从8阶降到4阶，在消除增根的同时还提高了计算速度。然后通过矩阵分解特征值求解关节变量，保证了逆运动学解的准确性和精度。最后借助Maple数学计算软件验证逆运动学算法的正确性，采用VC++语言和CLAPACK数学运算库实现运动学算法的仿真。验证结果表明，利用该算法求解运动学逆解仅需0.67ms，相对传统的反变换法具有更优的实时高精度性能。

四关节机械手；逆运动学；矩阵分解；实时高精度

机械手位姿的变化通过各关节的运动来实现，因此任务空间的运动必须转换到各关节空间，而逆运动学算法是关节角与三维位姿之间的转换纽带，所以逆运动学算法的实时精确性是机械手轨迹规划与运动优化控制的基础。

王战中[1]等人提出了用MATLAB GUI编程来自动求解机器人的多组逆解，并采用最短行程的原则自动寻找机器人的最优逆运动学解。李宪华[2]等人针对纯代数法找不到六自由度模块化串联机械臂的独立不相关变量方程的问题，采用几何方法求解机械臂前3个关节和反变换法求解后3个关节，并通过给出解的组合原则，得到了该机械臂逆运动学的完整解析解。程永伦[3]和刘华山[4]等人基于变换矩阵中旋转子矩阵正交的特性，提出了一种6R机器人运动学逆解算法。S. KUMAR[5]等人将冗余机械臂逆运动学求解问题转化为非线性优化问题。Van Henten[6]等人将混合数值解析法引入到黄瓜采摘机器人逆运动学求解问题中，提高了算法的稳定性和效率。

本文针对自主研发的NGR01型四关节机械手[7]，通过符号运算和矩阵分解求运动学逆解，不仅提高了计算运动学逆解的速度，同时还降低了浮点数运算带来的累积误差。四关节机械手的实数运动学逆解最多有4组，但考虑到机构设计及实际工程应用中各关节角的有效范围，最终满足要求的机械手逆运动学解最多有2组。

1 逆运动学方程演算

机械手逆运动学含义为：已知三维空间中机械手关节末端的位姿矩阵，要求出对应的各关节变量。根据D-H矩阵坐标变换原则，四关节机械手运动学方程可以描述为：

TEnd=T1T2T3T4

变形可得：

(1)

Ti=Rz(θi)Tz(di)Tx(ai)Rx(αi)

(i=1,2,3,4)

式中：Ti为第i个连杆相对于第(i-1)个连杆的位姿转换矩阵；TEnd为机械手末端坐标系相对于基坐标系的位置和姿态；Rz和Rx为姿态变换矩阵；Tz和Tx为位置变换矩阵；di，ai和αi为机械手结构参数，由具体机械手结构确定；θi为关节变量。

现将D-H参数作为符号变量，采用以符号运算著称的数学软件Maple对式(1)左右两边分别进行计算，可知第3列和第4列元素与θ4无关，从而得到关于θi(i=1,2,3)的6个方程，以矩阵形式表示为：

(2)

(3)

式中：f1=g1+g2+a3，f2=λ3(g2-g1)，f3=μ3(g1-g2)+d3，r1=m1+m2，r2=λ3(m2-m1)，r3=μ3(m1-m2)，g1=c3a3，g2=λ3a3，m1=s3λ3，m2=λ3μ3，h1=c1a4+s1d4-a1，h2=-μ1d1-λ1(s1a4-c1d4)，h3=μ1(s1a4-c1d4)+λ1d1，n1=c1μ4-s1λ4，n2=-λ1(s1μ4-c1λ4)，n3=μ1(s1μ4-c1λ4);μi=sinαi，λi=cosαi，si=sinθi，ci=cosθi，i=1,2,3,4。

进一步将式(2)和式(3)进行变换，构造出两个新的矢量等式P和L，有：

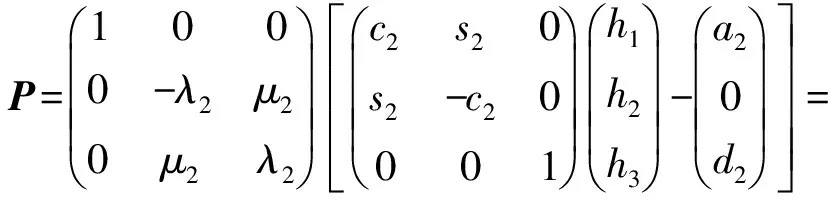
式中：hv=FSC(c1,s1,c2,s2)，fv=FSC(c3,s3)，nv=FSC(c1,s1,c2,s2)，rv=FSC(c3,s3)，其中v=1,2,3，FSC(·)表示关节变量正余弦函数的组合。

采用符号运算对P和L做乘法，由P，L，P·P，P·L，得到8个逆运动学方程：

PL1(θ1,θ2)=PR1(θ3)

(4)

PL2(θ1,θ2)=PR2(θ3)

(5)

PL3(θ1,θ2)=PR3

(6)

LL1(θ1,θ2)=LR1(θ3)

(7)

LL2(θ1,θ2)=LR2(θ3)

(8)

LL3(θ1,θ2)=LR3

(9)

(P·P)L1(θ1,θ2)=(P·P)R1

(10)

(P·L)L2(θ1,θ2)=(P·L)R2

(11)

式中：下标L和R分别表示矢量等式的左式和右式，1，2，3是矢量中元素的标号。

可见，式(6)、式(9)～(11)共4个等式与θ3无关，将这4个等式合并后组合成矩阵形式：

(12)

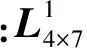
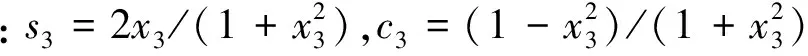
代入含有θ3的4个等式，线性变换后得到4个新的等式：

PL1(θ1,θ2)+x3(PL2(θ1,θ2))=

PR1(θ3)+x3(PR2(θ3))

(13)

PL2(θ1,θ2)-x3(PL1(θ1,θ2))=

PR2(θ3)-x3(PR1(θ3))

(14)

LL1(θ1,θ2)+x3(LL2(θ1,θ2))=

LR1(θ3)+x3(LR2(θ3))

(15)

LL2(θ1,θ2)-x3(LL1(θ1,θ2))=

LR2(θ3)-x3(LR1(θ3))

(16)

同理，将式(13)～(16)这4个等式合并，用矩阵形式表示：

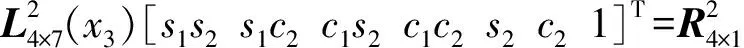
(17)

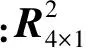
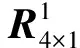
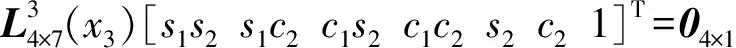
(18)

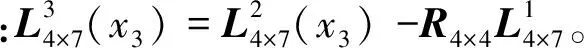
令xi=tan(θi/2)，i=4,5,则有：

(19)

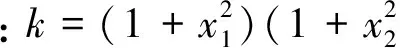
为方便表述，将式(19)简化为：

L5(x3)(V12)=0

(20)

式中：L5(x3)=Ax3+B，为常系数矩阵，其中A∈R4×4，B∈R4×7；V12为包含θ1和θ2的半角正切以及正余弦函数的向量。

2 矩阵分解求根

式(20)有解的必要条件是：

det(L5(x3))=0

(21)

式(21)是关于x3的一元四次方程，通过求方程的解可得到x3的4个根，从而解出θ3。求得x3后,将其带入式(19)可求出x1和x2的解,由于求解一元四次方程的计算量较大,且最终解的精度会受运算过程中累积误差的影响,为克服该问题,采用矩阵分解法化解式(21)。

设A为非奇异矩阵，由方程det(L5(x3))=0可以得到：

Ix3+A-1B=0

(22)

式中：I为4阶单位矩阵。

令M=A-1B，由矩阵理论可知，矩阵M的特征值即为x3的解，对应的特征矢量即为V12。由V12中的相关元素可以计算出x1和x2，从而解出θ1和θ2，继续将求出的3个关节变量代入式(1)，即可求得θ4。为降低累积误差对关节变量解的影响,运算的过程数据需要保留较高数量级。

3 基于VC++的算法实时求解

分解矩阵R4×4和A的奇异值，求解矩阵M的特征矢量和特征值，均具有较高的运算复杂度。为了实现NGR01型机械手运动学逆解的实时计算，采用C++将CLAPACK编译成blas.lib、libF77.lib、libI77.lib和clapack.lib 4个库文件，调用其中的相关函数进行矩阵计算。CLAPACK是由f2c编译成Fortran77 LAPACK线性代数库的C语言版本，以目前最有效的线性运算内核blas做底层计算，具有简洁、高效和可移植性等优点。

a.头文件包含处理。

因为程序是C++，而CLAPACK是f2c程序转换的C语言版本，所以用extern关键字调用。

extern"C"

{

#include

#include

}

b.关键函数的调用。

dgesvd_的功能是对一个实矩阵进行矩阵奇异值分解。gesvd_的函数声明如下:

GLfloat dgesvd_(char *jobu, char *jobvt, integer *m, integer *n, doublereal *a, integer *lda, doublereal *s, doublereal *u, integer * ldu, doublereal *vt, integer *ldvt, doublereal *work, integer *lwork, integer *info)

Dgeev_的功能是对一个实矩阵进行矩阵特征值分解。dgeev_的函数声明如下:

GLfloat dgeev_(char *jobvl, char *jobvr, integer*n, doublereal*a, integer*lda, doublereal* wr, doublereal *wi, doublereal *vl, integer *ldvl, doublereal *vr, integer *ldvr, doublereal *work, integer *lwork, integer *info)

4 实例求解与数字仿真

以自主开发的NGR01[7]型四自由度机械手为对象开展逆运动学验算实验。机械手连杆坐标系如图1所示，D-H参数见表1。仿真计算机平台配置为：Intel酷睿双核处理器，2GB DDR3内存，Windows XP操作系统。

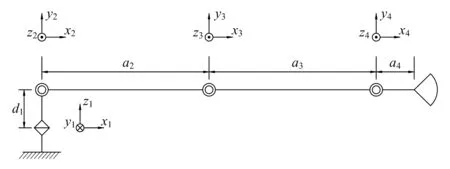
图1 NGR01型机械手连杆坐标系

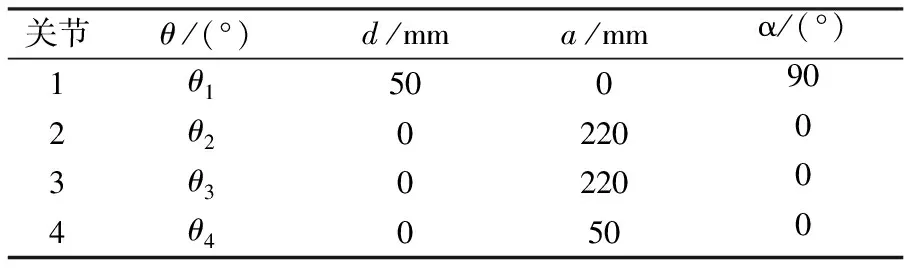
表1 NGR01型机械手连杆参数

设四关节机械手末端位姿矩阵为：

设置Maple的Digits环境参数为15时，求出与Tend0对应的满足要求的2组运动学逆解，结果见表2。

表2 2组运动学逆解

现将每组关节变量代入Tend=T1T2T3T4中，得到2个末端位姿矩阵Tend_i(i=1,2)，令误差矩阵为e，e(r,c)(r,c=1,2,3,4)为e的第r行第c列元素，其计算表达式为：

则有：

在VC++ 6.0环境中，基于MFC框架类，通过CLAPACK数学运算库实现逆运动学算法的仿真。以1 500次测试计算关键数值所需时间，得到如表3所示的结果，可见，算法的平均耗时为0.671 1ms。在相同仿真条件下，用反变换法求解逆运动学的平均耗时为1.13ms，因此提出的算法比反变换法具有更好的实时性。

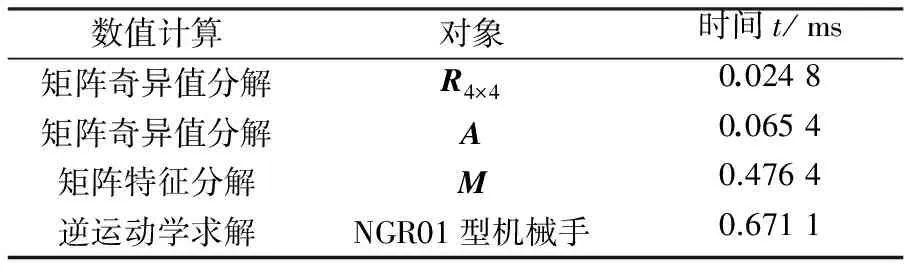
表3 数值计算所需时间

基于VC++仿真环境及OpenGL图形库仿真出机械手的运动学过程，NGR01型机械手的逆运动学解对应的位姿仿真结果如图2所示。在工程实际应用中，为了缩短机械手运动时间，并降低机械手能量的消耗，最优逆运动学解通常选取距当前关节变量距离最小的一组。

5 结束语

本文采用矩阵特征分解方法计算关节变量，从特征值和特征向量中快速求出3个关节变量，进一步得到四关节机械手最多4组逆运动学解。借助Maple数学计算软件、VC++语言和CLAPACK数学运算库实现整套运动学算法的仿真和验证，基于OpenGL图形库仿真出机械手的运动学过程。文中提出的整套算法具有实时高精度特性，完全能够满足NGR01型四关节机械手的实时控制需要，是一种比较理想的逆运动学求解方案，本论文提出的算法将应用于智能型花卉采摘机械手控制系统中。

图2 NGR01型机械手的2种姿态

[1] 王战中，杨长建，刘超颖，等．MATLAB环境下六自由度焊接机器人运动学逆解及优化[J]．机械设计与制造，2013(7)：182-184.

[2] 李宪华，郭永存，张军，等．基于MATLAB的模块化机器人手臂运动学算法验证及运动仿真[J]．计算机应用研究，2013，30(6)：1682-1684，1704.

[3] 程永伦，朱世强，刘松国．基于旋转子矩阵正交的6R机器人运动学逆解研究[J]．机器人，2008，30(2)：160-164.

[4] 刘华山，朱世强，吴剑波，等．基于向量内积的机器人实时逆解算法[J]．农业机械学报，2009，40(6)：212-216.

[5] Kumar S，Sukavanam N．An optimization approach to slove the inverse kinematics of redundant manipulator[J]．Information and System Sciences, 2010，6(4)：414-423.

[6] Van Henten，Schenk E. J．Collision-free inverse kinematics of the redundant seven-link manipulator used in a cucumber picking robot[J]．Biosystems Engineering，2010，106(2)：223-330.[7] 汪木兰，徐开芸，饶华球，等．虚实结合的多关节机器人开放式仿真系统研究[J]．系统仿真学报，2007，19(21)：4965-4969.

InverseKinematicsAlgorithmforFourJointManipulatorBasedonMatrixDecomposition

LI Xiaoxia1, WANG Mulan2, YIN Hongmei3, XU Yunfei1

(1.Jiangsu Food & Pharmaceutical Science College, Jiangsu Huaian, 223003, China)(2.Nanjing Institute of Technology, Jiangsu Nanjing, 211167, China)(3.Huaian College of Information Technology, Jiangsu Huaian, 223003, China)

It proposes a real-time inverse kinematics algorithm with high accuracy based on the kinematics equation of manipulator with the research object of self-developed NGR01 type four joints manipulator. This reduces the order of matrix equation from 4 to 2 through symbolic calculating, thus eliminates extraneous roots while improving the algorithmic speed. Eigen-decomposition is adopted to get roots from target matrix, which ensures the accuracy of the solutions. The correctness of the algorithm is verified by Matlab and Maple mathematical software. It uses C++ language and CLAPACK math library to realize the simulation of kinematics algorithm. Experimental results indicate that the presented algorithm can acquire 2 inverse kinematics solutions in a time of 0.67 ms, so the proposed algorithm is faster and higher accuracy than the traditional inverse transformation method with the same experiment platform.

Four Joint Manipulator; Inverse Kinematics; Matrix Decomposition; Real-time & High Accuracy

10.3969/j.issn.2095-509X.2014.09.007

2014-05-10

淮安市科技项目(SN13064)；江苏省高校自然科学研究基金项目(13KJB120003)

李小霞(1987—)，女，江苏淮安人，江苏食品药品职业技术学院助教，工学硕士，主要研究领域为机器人技术和先进制造技术。

TP241.2

A

2095-509X(2014)09-0027-04