Einstein场方程的Schwarzschild求解——广义相对论经典算例*1

陈英明，谭明涛，章志敏

(1.淮北师范大学物理与电子信息学院，安徽 淮北 235000；2.电子科技大学物理电子学院，四川 成都 610054；3.吉首大学物理与机电工程学院，湖南 吉首 416000)

Einstein场方程的Schwarzschild求解
——广义相对论经典算例*1

陈英明1,2，谭明涛3，章志敏1,2

(1.淮北师范大学物理与电子信息学院，安徽 淮北 235000；2.电子科技大学物理电子学院，四川 成都 610054；3.吉首大学物理与机电工程学院，湖南 吉首 416000)

Einstein场方程是一个难解的非线性二阶微分方程组，其解析求解广泛应用于广义相对论.求解了Einstein场方程的中心对称静态解，即Schwarzschild解，该解对于广义相对论的研究具有一定的指导作用.

广义相对论；Einstein场方程；Schwarzschild解；黑洞

广义相对论是相对论性的引力理论[1]，强等效原理[1-2](对于一切自然规律，局域范围内无法区分引力与惯性力)则是广义相对论的基本假设之一.另一个基本假设是广义协变原理[2-3]，即所有的参考系都是平权的，在任意的坐标变换下，一切的物理规律都是协变的.因此，在广义相对论中，坐标系统的选取可以是任意的，习惯上称dx0为坐标时间，dxα(α=1,2,3)为坐标距离.

Einstein在20世纪初建立起来的广义相对论使得人们对于引力和时空有了全新的认识，引力理论及其在相关领域的研究获得了空前的发展，不断地涌现新的观念.当人们在研究质量超过中子星临界质量的恒星时，发现简并的中子气体产生的简并压力无法抵抗非常强大的引力作用，从而使得恒星不断收缩，于是出现了由广义相对论所预言的一类由大质量恒星演化而来的特殊天体，即黑洞[2-3].笔者引入黑洞这一重要的概念，研究了在广义相对论中如何通过解析求解Einstein场方程的中心对称静态解.

1 理论推导

场的中心对称性要求度规或间隔ds在所有与中心等距离点处必须是一样的.当引力场存在时，时空是非Euclid的，因此这个距离不是坐标r.当作坐标变换φ→-φ或ϑ→-ϑ时ds不变；再考虑到静态引力场，t→-t时也有ds不变.于是中心对称静态度规的形式为[1-3]

ds2=A(r)c2dt2-B(r)(dϑ2+sin2ϑdφ2)-C(r)dr2，

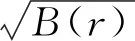
ds2=A′(r′)c2dt′2-B′(r′)dr′2-r′2(dϑ′2+sin2ϑ′dφ′2).

(1)

略去(1)式中坐标的撇号(即重新标记坐标)，并令A′(r)=e2ν,B′(r)=e2λ,其中ν和λ都是r的函数，进而得到间隔为

ds2=e2νc2dt2-e2λdr2-r2(dϑ2+sin2ϑdφ2).

则协变度规gik的矩阵为

(2)

相应的逆变度规张量为

(3)

其中：x0=ct；x1=r；x2=ϑ；x3=φ.由(2)，(3)式可知完整的克里斯多菲符号为

因为当i≠k时，总有gik=gik=0，所以

容易验算，克里斯多菲符号的64个分量中只有13个分量不为零，其余的51个则均为0，即

(4)

利用克里斯多菲符号还可以进一步计算里奇张量为

(5)

将(4)式代入(5)式可知

(6)

考虑Schwarzschild外部解，即引力源以外的区域，显然有

Rik=0，

(7)

将(7)式代入(6)式可得

(8)

当r→时，时空是平坦的，黎曼空间度规退化为闵可夫斯基空间度规，从(8)式的微分方程组可以解得度规为

相应的线元表示为

(9)

(9)式即为Schwarzschild的外部解，描述了球对称物体外部的引力场.

2 结语

Schwarzschild外部解有2个奇点：一个是本性奇点r=0，另一个奇点r=rs=GM/c2为Schwarzschild半径.Schwarzschild半径与黑洞密切联系，黑洞为广义相对论的理论预言[1-3]，但是在早期的研究中，研究者认为宇宙中不可能有物体能够达到如此高的密度，即全部的质量M都集中在Schwarzschild半径rs=GM/c2之内.例如，太阳的Schwarzschild半径rs≈3 km，地球的Schwarzschild半径rs≈9 mm.rs是一个球面型界面，界面内外的时空特性完全不同，此界面被称作黑洞的视界.黑洞的认证十分困难，无光线发出，只能采用间接的方式来考察.如：双星系统中有一个是黑洞，则可以利用引力透镜效应来观察.

1974年霍金在考虑量子效应的情况下已证明黑洞也可以存在辐射，缓解了广义相对论与热力学之间的矛盾，同时也揭示了热力学、量子力学[4]与广义相对论之间的一些联系[5].如今，黑洞物理学已经成为宏观世界的引力理论[6]与微观世界的量子理论相互联系的纽带，并向量子力学、热力学、弦理论[7]、统计物理学等学科与广义相对论相互交叉的研究领域发展[1,5,8].

[1] 王永久.黑洞物理学[M].长沙:湖南师范大学出版社,2000：1-124.

[2] CHANDRASEKHAR S.The Mathematical Theory of Black Holes[M].New York:Oxford University Press,1983:1-97.[3] RUFFINI R，WHEELER J A.Introducing the Black Hole[J].Phys. Today,1971,76(1):30.

[4] PERES A，TERNO D R.Quantum Information and Relativity Theory[J].Rev. Mod. Phys.,2004,76:93.

[5] 史蒂芬·霍金，罗杰·彭罗斯.时空本性[M].杜欣欣，吴忠超，译.长沙:湖南科学技术出版社,1996：1-113.

[6] MISNER C W,THORNE K S，WHEELER J A.Gravitation[M].San Francisco:Freeman,1973：1-89.

[7] POLCHINSKI J.String Theory[M].Cambridge:Cambridge University Press,1998:1-45.

[8] TEUKOLSKY S A.Rotating Black Holes:Separable Wave Equations for Gravitational Electromagnetic Perturbations[J].Phys. Rev. Lett.,1972(29):1 114.

(责任编辑 陈炳权)

SchwarzschildSolutionofEinsteinFieldEquations: A Classical Example for General Relativity Teaching

CHEN Yingming1,2,TAN Mingtao3,ZHANG Zhiming1,2

(1.School of Physics and Electronic Information,Huaibei Normal University,Huaibei 235000,Anhui China;2.Institute of Applied Physics,University of Electronic Science and Technology of China,Chengdu 610054,China;3.College of Physics and Electromechanical Engineering,Jishou University,Jishou 416000,Hunan China)

Einstein field equations are difficult nonlinear second order differential equations,but its analytical solutions are of considerable practical significance for general relativity teaching.This paper demonstrates the centrosymmetric static solutions of Einstein field equations in details,namely Schwarzschild solutions,which can play a guiding role for the beginners of general relativity and be a reference for the research of general relativity teaching.

general relativity;Einstein field equations;Schwarzschild solution;black hole

1007-2985(2014)04-0031-03

2014-03-21

淮北师范大学青年基金资助项目(700702)；安徽高校省级自然科学研究项目(KJ2013Z287)；国家自然科学基金资助项目 (61201089)

陈英明(1979-),男，淮北师范大学教师，电子科技大学博士，主要从事时间反演电磁学研究.

O412.1

A

10.3969/j.issn.1007-2985.2014.04.008