一种求解非线性互补问题的外梯度-Filter方法*1
龙 君,曾三云
(1.吉首大学民族预科教育学院,湖南 吉首 416000;2.吉首大学数学与统计学院,湖南 吉首 416000)
一种求解非线性互补问题的外梯度-Filter方法*1
龙 君1,曾三云2
(1.吉首大学民族预科教育学院,湖南 吉首 416000;2.吉首大学数学与统计学院,湖南 吉首 416000)
结合 Josephy Newton方法,建立了一种不含价值函数的求解非线性互补问题的全局策略.该策略基于外梯度步和Filter技术,提出一个外梯度-Filter算法.此算法中的外梯度步可以减少与最优解之间的距离,从而使该算法具有全局收敛性.在适当的条件下,该算法还具有超线性收敛性.
非线性互补问题;Filter技术;Josephy Newton方法;外梯度步;收敛性
考虑如下非线性互补问题(NCP(F))[1-2]:
F(x)≥0,xTF(x)=0x≥0,
其中向量x∈Rn,F:Rn→Rn为给定的二次连续函数.
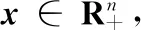
变分不等式与互补问题是2个相伴而生的问题.求解非线性互补问题的算法有很多,例如投影法、内点法、非光滑Newton法、光滑Newton法等[3].最近,文献[4]提出了一种求解单调非线性互补问题的Newton型方法,这种算法有以下优点:(1)从任意的初始点起,由算法所产生的迭代点列收敛到NCP(F)的一个解;(2)算法具有全局收敛性和超线性收敛性;(3)不依赖于任何的价值函数.
实际上,求解非线性互补问题还有一种简单的方法叫做外梯度法.一方面,它因计算简单、存贮量小等优点而广受众多学者的关注.另一方面,Filter方法也因其良好的数值结果而广受关注.因此,笔者借鉴文献[1]的部分思想,对文献[4-5]中算法进行了适当的修正,即将外梯度法与Filter技术相结合,提出一个外梯度-Filter算法,在较弱的条件下证明了这种方法具有全局收敛性和超线性收敛性.
1 预备知识
1.1基本性质
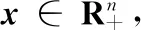
对任意的实数α>0,定义关于α的函数yα(x)∶=[x-αF(x)]+,并记yα(x)的自然剩余为E(α,x,F(x))=x-[x-αF(x)]+,则E(α,x,F(x))具有如下性质:

记NCP(F)的解集为X*,易知x∈X*当且仅当x=yα(x).若取α=1,则x∈X*当且仅当E(1,x,F(x))=x-[x-F(x)]+=0.
对于一个给定的点xk,运用Josephy Newton方法[6-7]可求解如下线性互补问题LCP(φk):
φk(x)≥0,xTφk(x)=0x≥0,
(1)
其中
φk(x)∶=F(xk)+(Gk+μkI)(x-xk),
(2)

1.2Filter技术
首先介绍Filter方法的一些相关定义和性质[8].
对于某种最优化方法,希望发现一个满意的点,它不仅与目标函数相关,而且与约束条件也有联系.现定义与目标函数、约束条件相关的2个函数为h(x)=‖[F(x)]-‖,p(x)=‖xTF(x)‖2+σh(x),其中[F(x)]-=max{0,-F(x)},σ是一个常数,x≥0总是得到满足.
定义1[8]一个点对(h(xk),p(xk))占优另一个点对(h(xi),p(xi)),当且仅当h(xk)≤h(xi)且p(xk)≤p(xi),记作xk⪯xi.
由此概念,可以定义一个Filter集合,在文中所给的算法中,它将被用作接收或拒绝一个试探点的准则.
定义2[8]Filter集合是指这样一个序列点对(h(xk),p(xk))所组成的集合,使得彼此之间不相互占优.若点对(h(xk),p(xk))不被Filter集合中的其他点对所占优,则说它是可以接受的.
2 外梯度-Filter算法
结合外梯度法与Filter技术,提出一个新的算法,即外梯度-Filter算法.
算法1[外梯度-Filter算法]

步骤3(不精确牛顿步) 若‖E(1,xk,F(xk))‖=0,则停.否则,选择一个正半定矩阵Gk和μk=‖E(1,xk,F(xk))‖t.取ρk∈[0,1),计算由(1),(2)式给出的LCP(φk)的一个非精确解zk≥0,使得‖E(1,zk,φk(zk))‖≤ρkμk‖xk-zk‖.
步骤4 令yk∶=zk-ek,vk∶=F(yk)-φk(zk)+E(1,zk,φk(zk)),设εk∶=-vk+μk(xk-yk).若‖εk‖>σkμk‖xk-yk‖,则转步骤6.



下面给出算法1对应的修复算法.
算法2[修复算法]
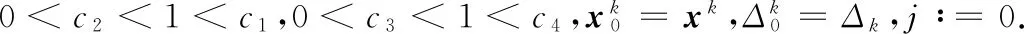

步骤3 计算
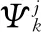
(3)
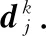
3 收敛性分析
假设NCP(F)的解集是非空的.
定义3[9]映射F:Rn→Rn在集合S上是:(ⅰ) 伪单调的,如果对任意的向量x,y∈S有F(y)T(x-y)≥0⟹F(x)T(x-y)≥0;(ⅱ) 单调的,如果对任意的向量x,y∈S有[F(x)-F(y)]T(x-y)≥0.
显然,若F在S上单调,则它在S上一定伪单调.另外,若映射F是连续且伪单调的,则对应的VIP(F)的解集是闭凸集[10].
分析算法的收敛性之前,需要先做一些假设,具体如下:
(H1) 集合{xk}⊂X非空有界;
(H2) 函数F(x)在包含于X的开集上二次连续可微;

(H4) 矩阵序列{Gk}有界;
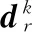
需要注意的是:(H1)和(H2)是标准假设;(H3)是个很弱的充分下降条件(因为Cauchy步满足这个条件),在文中,它作为一个充分条件;在信赖域方法里,(H3)能保证全局收敛性;(H4)是得到收敛结果的重要条件,但它对局部收敛速度的影响较小.
通过对修复算法的分析,有如下结论:
引理2[11-12]在假设(H1)—(H5)条件下,修复算法有限步终止.


定理1 假设映射F是连续和伪单调的,{xk}由算法1产生,则{xk}是有界的.进一步假设存在常数C1,C2>0,使得对于∀k,有

则{xk}收敛到NCP(F)的一个解上.
由于篇幅限制,定理1的证明过程省略.定理1表明,在较弱的条件下,文中所提出的算法具有全局收敛性.
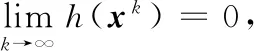
定理2的结论满足了NCP的要求,即F(x)≥0.
借鉴文献[4]中的证明方法,可以得到文中所给算法的超线性收敛性如下:
定理3[4]假设映射F是连续和单调的,设x*是NCP(F)的一个解,在这个解上,F是可微的且F(x*)正定,设F在x*的附近是度为p∈(0,1]的局部Hölder连续的.另外,假设且从某一指标k0起,Gk=F(xk),则序列{xk}Q-超线性收敛到x*.
4 结语
在迭代过程中,结合Josephy Newton方法,对正交投影步或外梯度步运用Filter技术,提出了一种求解非线性互补问题的新算法,并得到此算法的全局收敛性,在适当的条件下,该算法还具有超线性收敛性.
[1] HORST R,PARDALOS P.Complementarity Problems[M]∥Hankbook of Global Optimization.Boston,Massachusetts:Kluwer Academic Publishers,1995:271-338.
[2] FERRIS M C,PANG J S.Complementarity & Variational Problems:State of the Art[M].Philadelphia VSA:SIAM,1997.
[3] 韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:科学技术出版社,2006.
[4] SOLODOV M V,SVAITER B F.A Truly Globally Convergent Newton Type Method for the Monotone Nonlinear Complementarity Problem[J].SIAM J. OPTIM,2000,10(2):605-625.
[5] CALAMAIA P H,MORE J J.Projected Gradient Methods for Linearly Constrained Problems[J].Math. Prog.,1987(39):93-11.
[6] BONNANS J F.Local Analysis of Newton Type Methods for Variational Inequalities and Nonlinear Programming[J].Applied Mathematics and Optimization,1994,29(2):161-186.
[7] JOSEPHY N.Newton’s Method for Generalized Equations[R].Madison,Wisconsin:Mathematics Research Center,University of Wisconsin,1979.
[8] FLETCHER R,LEYFFER S.Nonlinear Programming Without a Penalty Function[J].Math. Prog.,2002(91):239-269.
[9] QU Bao,WANG Changyu,ZHANG Shuxi.A Method for Solving Nonlinear Complementarity Problems and Its Convergence Properties[J].Math. Nume. Sini.,2006,28(3):247-258.
[10] FACCHINEI F,PANG JONG SHI.Finite Demensional Variational Inequalities and Complementarity Problems[M].New York:Spring Verlag,2003.
[11] LONG Jun,MA Changfeng,NIE Puyan.A New Filter Method for Solving Nonlinear Complementarity Problems[J].Applied Mathematics and Computation,2007(185):705-718.
[12] LONG Jun,MA Changfeng.A Filter Method for Solving Nonlinear Complementarity Problems Based on Derivative Free Line Search[J].Applied Mathematics and Computation,2007(190):271-286.
[13] LONG Jun,ZENG Sanyun.A Projection Filter Method for Solving Nonlinear Complementarity Problems[J].Applied Mathematics and Computation,2010,216(1):300-307.
[14] LONG Jun,ZENG Sanyun.A New Filter Levenberg Marquardt Method with Disturbance for Solving Nonlinear Complementarity Problems[J].Applied Mathematics and Computation,2010,216(2):677-688.
(责任编辑 向阳洁)
ExtragradientFilterMethodforSolvingNonlinearComplementarityProblems
LONG Jun1,ZENG Sanyun2
(1.School of Preparatory Education for Minority Nationalities,Jishou University,Jishou 416000,Hunan China;2.College of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China)
Combined with the Josephy Newton method,a new globalization strategy without any merit function was established for nonlinear complementarity problem.The strategy presents an extragradient filter algorithm based on extragradient step and filter technology.The extragradient step can reduce the distance with the optimal solution of the problem.So the resulting algorithm is globally convergent to a solution.Under natural assumptions,locally superlinear rate of convergence can be obtained.
nonlinear complementarity problem;filter technology;Josephy Newton method;extragradient step;convergence
1007-2985(2014)04-0019-04
2013-11-04
湖南省教育厅科学研究项目(10C1126,10B088)
龙 君(1973- ),男,湖南凤凰人,吉首大学民族预科教育学院讲师,博士生,主要从事基于Filter方法的理论与算法研究.
O224
A
10.3969/j.issn.1007-2985.2014.04.005

