考虑非牛顿流体螺旋流动的钻井井筒温度场研究

李梦博， 柳贡慧,2， 李 军， 魏晓强， 高海军

(1.中国石油大学(北京)石油工程学院，北京 102249；2.北京信息科技大学，北京 100192；3.中国石油长城钻探工程有限公司钻井三公司，辽宁盘锦 124010；4.中国石油长城钻探工程有限公司钻井一公司，辽宁盘锦 124010)

钻井过程中的井筒温度分布对计算钻井液循环当量密度非常重要，而且，井筒温度分布还是进行井壁稳定性分析和解释井筒呼吸效应的关键参数，因此,准确了解钻井过程中井筒温度及其变化规律对于安全、高效钻进具有重要的意义。自20世纪60年代以来，国内外很多学者[1-5]对钻井循环过程中井筒温度的分布进行了研究，提出了不同的理论模型与求解算法，但现有的模型仅考虑了由钻柱旋转而产生的摩阻扭矩热源项对井筒温度的影响，未针对钻柱旋转问题进行更为深入的研究，无法准确描述和定量解释在钻柱旋转条件下井筒温度场的变化规律。钻井液在循环过程中表现为非牛顿流体的流动特性，由钻柱旋转所引起的环空中非牛顿流体螺旋流动使钻井过程中井筒内的传热过程更为复杂。因此，有必要针对非牛顿流体的流动特性建立综合考虑钻柱旋转的井筒循环温度场模型，认清非牛顿流体螺旋流动情况下井筒温度场的变化规律,并对温度进行定量预测。

1 温度场模型的建立

1.1 基本假设

建立温度场模型时做了以下基本假设：1)由于钻遇地层大部分为层状岩石，其热导率具有各向异性，一般情况下其垂直层面的热导率小于平行层面的热导率，因此，忽略地层中垂向上的热传导，仅考虑水平方向的热传导；2)忽略钻杆、套管和水泥环的热惯量，由于钻杆、套管和水泥环的壁厚与井眼直径比相对较小，因此，可采用综合传热系数来代替该区域的瞬态传热计算[6]；3)地层内不存在流体的流动，忽略岩石中的内热源；4)钻井液循环时，忽略钻井液轴向导热和钻井液的径向温度变化；5)在一定时间内，由于钻进井深的增量小于模型计算的空间步长，因此可视为钻井测深没有变化。

1.2 温度场模型的控制方程

取钻柱、环空和地层做研究对象，根据热力学第一定律可知，由外界进入单元体的净热量与外界对单元体所做的功之和等于单元体内能的增量，据此建立不同单元内的温度场控制方程。

1.2.1 钻柱内与环空内温度场控制方程

圆柱坐标系下钻柱内和环空内的能量守恒方程[7]分别为：

(1)

hafπdb(tw-ta)-πdpohpa(ta-tp)+

式中：ρm为钻井液密度，kg/m3；tp为钻柱内温度，℃；cm为钻井液比热，J/(kg·℃)；qm为流体的流量，m3/s；ta为环空温度，℃；tw为环空井壁处温度，℃；hpa为钻柱与环空的综合传热系数，W/(m2·℃)；haf为环空与地层的综合传热系数，W/(m2·℃)；Sp为钻柱内热源项，W/m；Sa为环空热源项，W/m；db为钻头直径，m；dpo为钻柱或钻铤外径，m；dpi为钻柱的内径，m；t为时间，s；z为井筒轴线方向的井深，m。

1.2.2 地层内温度场控制方程

基于模型假设，圆柱坐标系下地层的能量守恒方程为：

(3)

式中：λeff为等效热传导率，W/(m·℃)；tf为地层温度，℃；(ρc)eff为单位控制体内的等效容积热容量，J/(m3·℃)。

由于地层岩石为孔隙型介质，在传热计算过程中必须考虑地层的孔隙特性，等效热物理参数可用以下2式表示。

λeff=λgφλf(1-φ)

(4)

(ρc)eff=(ρc)f(1-φ)+(ρc)gφ

(5)

式中:φ为地层的孔隙度；λg为地层孔隙中油气水的热导率，W/(m·℃)；(ρc)f为地层岩石单位控制体内的容积热容量，J/(m3·℃)；λf为地层岩石的热导率，W/(m·℃)；(ρc)g为地层孔隙中油气水单位控制体内的容积热容量，J/(m3·℃)。

1.3 温度场模型辅助方程

1.3.1 热源项的计算

在钻井作业过程中，钻井泵和旋转系统分别向钻井系统提供水力学能量和机械能量。其中，一些能量用于破碎岩石和携带岩屑返出井筒，剩余的能量均以热量的形式耗散掉[8]，而这些耗散的热量直接影响井筒温度分布。热源项主要包括以下3部分：由钻井液流动黏性耗散产生的热量、钻柱与井壁旋转摩擦产生的热量和钻头破岩产生的热量。热源项的大小可以由水力学模型和摩阻扭矩模型来确定。针对钻井液非牛顿流体的流动特性，采用可以较准确描述其流变特性[9]的赫巴流变模式计算摩阻压降，采用高德利提出的模型[10]计算摩阻扭矩。

钻井液黏性耗散产生的热量主要表现在钻井液循环过程中摩阻压降的大小，由钻柱旋转产生的螺旋流动使摩阻压降的计算更加复杂。目前，通常采用轴向雷诺数Re及泰勒数Ta来描述旋转对摩阻压降产生的影响。Ahmed等人[11]利用量纲分析方法建立了非牛顿流体在钻柱旋转时与非旋转时摩阻压降比值的经验校正方法。旋转摩阻压降比值Rω的定义为：

(6)

由此，环空内单位控制体由黏性耗散所产生的热源项可表示为：

(7)

1.3.2 对流换热系数的计算

在环空和圆管中强迫对流换热系数通过努塞尔数Nu来进行计算[12]。努塞尔数的计算公式为：

(8)

式中:h为传热系数，W/(m2·℃);Dh表示环空的水力直径或钻柱的内径，m；λ为热导率，W/(m·℃)。

钻柱旋转时环空的传热模型可以简化成一个有轴向流动、内管旋转外管静止的同心圆管对流换热系统，如图1所示。由于有钻柱的旋转，环空内钻井液在轴向流动的同时会产生周向流动，表现为螺旋流动[13]，此时的对流换热系数受钻井液轴向流动和钻柱旋转的综合影响。Gazley等人[14]针对螺旋流的流动特性，利用等效雷诺数来对努塞尔数进行校正。

Nu=AReeffαPrγ

(9)

图1 有轴向流动内管旋转外管静止的同心圆管对流换热Fig.1 Convection heat transfer in concentric cylinders with axial flow,rotating inner cylinder and static outer cylinder

式中：Reeff为等效雷诺数；Pr为普朗特数；A，α和γ为通过试验确定的系数，取A=0.017，α=0.67，γ=0.33。

等效雷诺数定义为：

(10)

式中：ρ为钻井液密度，kg/m3；Dh为水力直径，m；veff为等效流速，m/s；μ为流体黏度，Pa·s；va为环空流速，m/s；ω为钻柱转速，rad/s；β为等效系数。

基于假设(2)，采用综合传热系数来代替钻杆、套管和水泥环处的瞬态传热计算，而综合传热系数的大小取决于流体的对流换热系数、钻杆与水泥环的热传导率等多个因素[15]。

1.4 边界条件

钻杆入口：

tp(z=0,t)=constant

(11)

井底：

tp(z=H,t)=ta(z=H,t)

(12)

地层：

tr(z,r=∞,t)=ts+ztg

(13)

井筒与地层边界面处：

(14)

式中：ts为地表温度，℃；tg为地温梯度，℃/m。

2 模型的求解方法

基于有限体积法，采用无条件稳定的Crank-Nicolson全隐式格式对温度场控制方程进行离散[16]，对每个控制体的控制方程，可以写成下面的一般格式。

(15)

式中：i为井筒轴线方向的空间节点；j为井筒径向方向的空间节点；n为时间节点。

把所有控制体的方程用矩阵形式表示，并采用高斯-赛德尔迭代方法进行求解，可求出每一时刻每一控制体的温度。

3 温度场模型验证与影响因素分析

3.1 模型的验证

为验证模型的可靠性，采用自主研制的PWD在华北油田某井进行了现场试验[17]。该井为生产井，设计井身结构为：一开，φ381.0 mm钻头×143.00 m；二开，φ215.9 mm钻头×2 570.00 m。在钻至井深2 000.00 m时起钻更换钻头，进行PWD试验。试验钻具组合为：φ215.9 mm PDC钻头+φ172.0 mm螺杆+浮阀+接头+φ171.5 mm随钻压力测量短节+接头+φ171.5 mm存储式压力测量短节+φ165.1 mm无磁钻铤×1根+稳定器+φ165.1 mm钻铤×5根+接头+φ127.0 mm加重钻杆×18根+φ127.0 mm钻杆+方钻杆。钻井参数：钻压40 kN，转速60 r/min，排量31 L/s，泵压17 MPa。钻井液性能：密度1.18 kg/L，漏斗黏度48 s，塑性黏度20 mPa·s，动切力8.17 Pa。

该试验主要分3个阶段：第1阶段为安装PWD下钻阶段；第2阶段为正常循环钻进阶段；第3阶段为钻柱不旋转仅循环阶段，以观察钻柱旋转对井底温度的影响。PWD测量数据和不同模型计算结果如图2所示。由图2可知：在开泵循环后，井底温度迅速下降，并最终趋于稳定；当钻柱停止旋转并继续循环时，井底温度继续降低并在大约30 min后趋于稳定，此时井底温度比正常钻进时低4 ℃左右。考虑井筒内热源项和钻柱旋转等因素模型的计算结果与现场试验测量数据吻合较好。

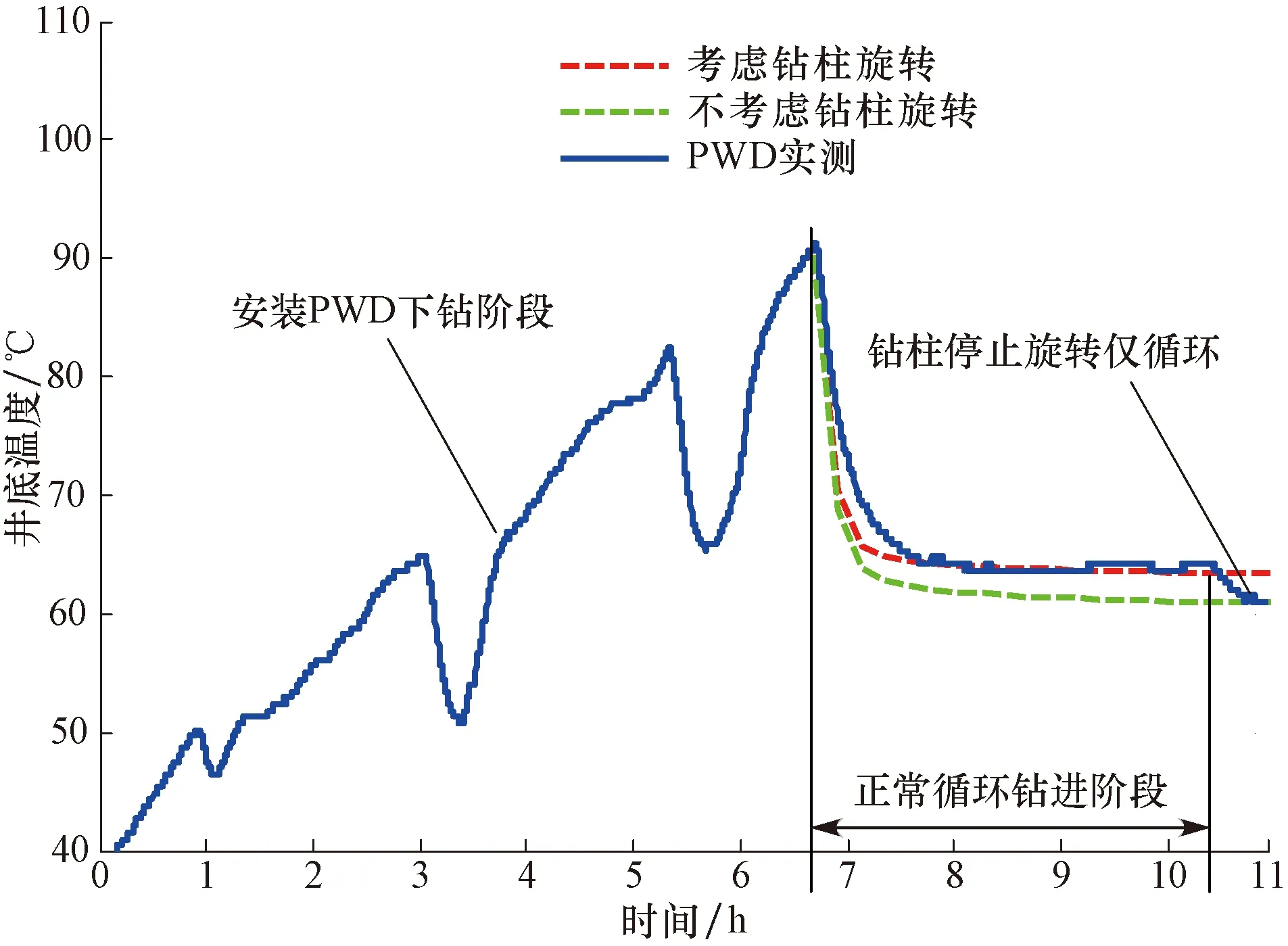
图2 现场试验测量数据与模型计算结果对比Fig.2 Comparison of on-site measured and model-caulated data

3.2 钻柱旋转对井筒温度场的影响

为了有效分析旋转对流体黏性耗散产生热源项的影响，以PWD试验井为计算实例分析其影响规律。图3为钻柱旋转对流体黏性耗散产生热源项影响的计算结果。由图3可看出：环空流体黏性耗散产生的热源项随着钻柱转速的增大而增大；在钻柱转速60 r/min时，由流体黏性耗散产生热源项的增大幅度为13%；在钻柱转速为180 r/min时，由流体黏性耗散产生热源项的增大幅度为18%。

图3 转速与环空流体黏性耗散产生热源项的关系Fig.3 Correlation between rotary speed and heat caused by viscous dissipation of annular fluids

图4为不同转速下轴向雷诺数和等效雷诺数的关系。由图4可看出，当环空内流体的流态为层流(轴向雷诺数Re<2 100)时，转速对等效雷诺数的影响较大，且随着转速的增大，等效雷诺数增大。在大排量或深井小井眼情况下，环空出现紊流(轴向雷诺数Re>2 100)，此时等效雷诺数与轴向雷诺数的比值接近于1，钻柱的旋转对等效雷诺数的影响不大。

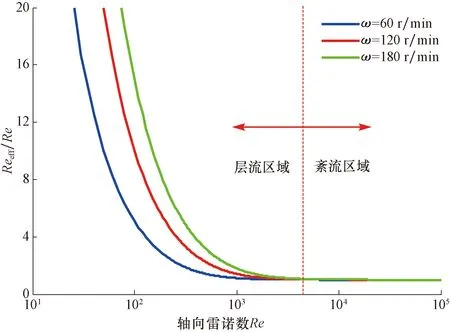
图4 轴向雷诺数和等效雷诺数的关系Fig.4 Relationship between axial Reynolds Number and Equivalent Reynolds Number

基于以上分析，并结合式(8)和式(9)可确定钻柱转速对环空与井壁对流换热系数的影响规律(见图5)。由图5可看出：在其他参数一定的情况下，环空流态无论是层流还是紊流，环空与地层对流换热系数均随着钻柱钻速的增大而增大；在环空流态为层流时，钻柱转速200 r/min时的对流换热系数与钻柱静止时相比增加14%；当环空流态为紊流时，对流换热系数相比于层流时大大增加，但钻柱转速200 r/min时的对流换热系数相比于钻柱静止时仅增加5%。因此，环空流体流态为层流时，钻柱转速对对流换热系数影响更为明显。

图5 钻柱转速对环空与井壁对流换热系数的影响Fig.5 Effect of rotary speed on coefficient of convection heat transfer between the annulus and the wellbore wall

由以上分析可知，钻柱旋转一方面使由钻井液黏性耗散产生的热源项增大，从而使整个环空温度上升；另一方面使环空与地层、环空与钻柱的对流换热系数增大，环空与钻柱内流体的换热量增大，使钻柱内的流体吸收更多的热量，从而使井底温度升高，环空与地层的换热量增大，地层中有更多的热量进入环空下部，导致井底温度进一步升高。

图6为不同井深条件下钻柱转速与井底温度的关系曲线。由图6可以看出，无论是浅井还是深井，钻柱转速对井底温度的影响规律是一致的，井底温度均随钻柱转速的增大呈指数增长，且随着井深的增深，钻柱旋转对井底温度的影响更加明显。对于井深2 000.00 m的试验井，不考虑钻柱旋转(钻柱转速为0)时的井底温度比钻柱转速为200 r/min时低4.5 ℃，而对于5 000.00 m井深的模拟井，不考虑钻柱旋转时的井底温度比钻柱转速为200 r/min时低7.8 ℃，这在计算井底温度时不能忽略。

图7为井深5 000.00 m时，不同因素对井筒环空温度剖面的影响关系曲线。由图7可以看出：当仅考虑对流换热系数的影响时，温度剖面与所建模型的计算结果相差不大，这说明由钻柱旋转导致的对流换热系数增大是导致井筒环空温度升高的主要原因；当仅考虑黏性耗散产生热源项的影响时，其温度剖面与不考虑钻柱旋转时的计算结果接近。因此，由钻柱旋转导致的黏性耗散热源项增大对井底温度的影响较小。

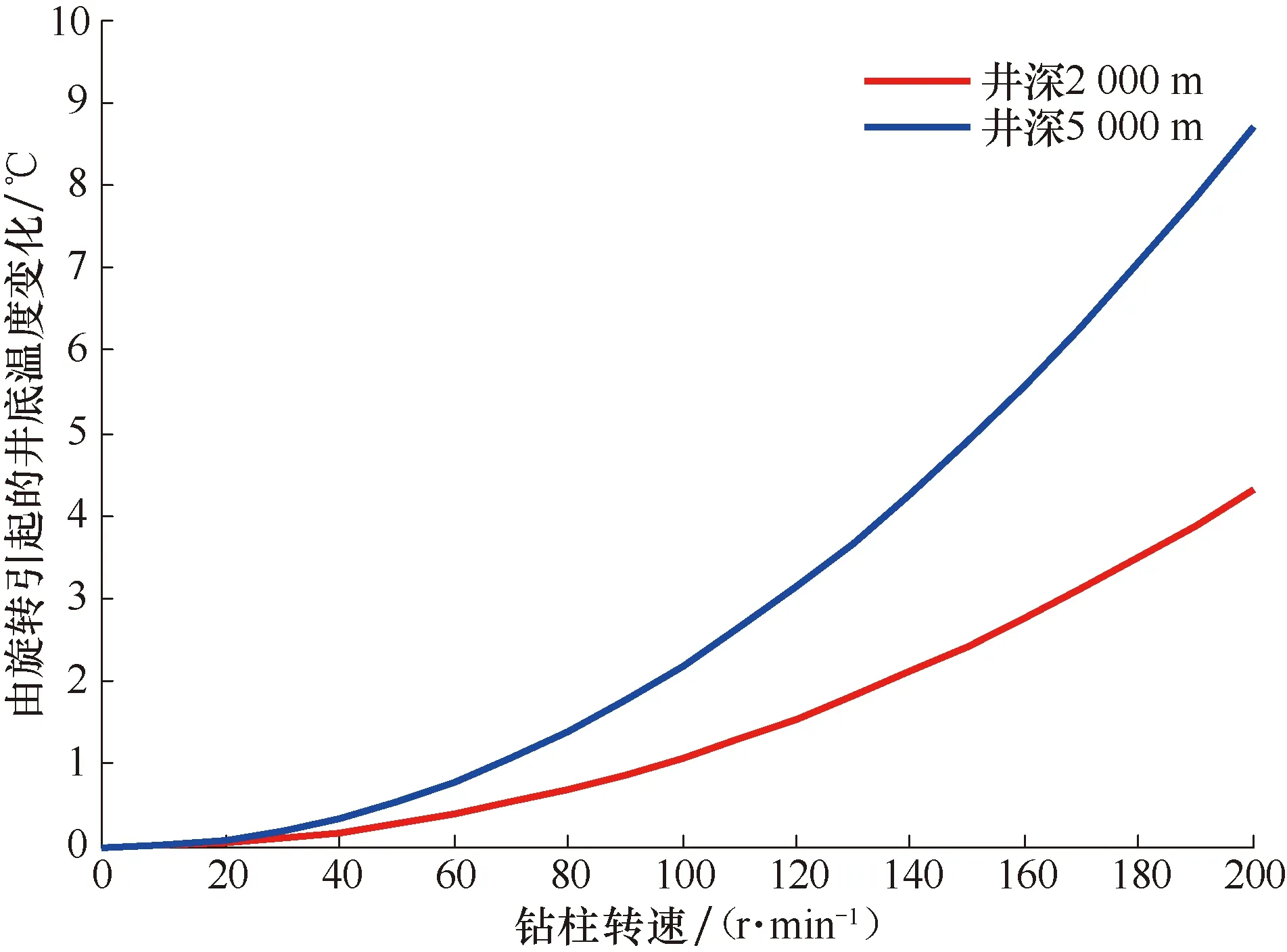
图6 钻柱转速与井底温度变化的关系Fig.6 Relationship between rotary speed and bottomhole temperature

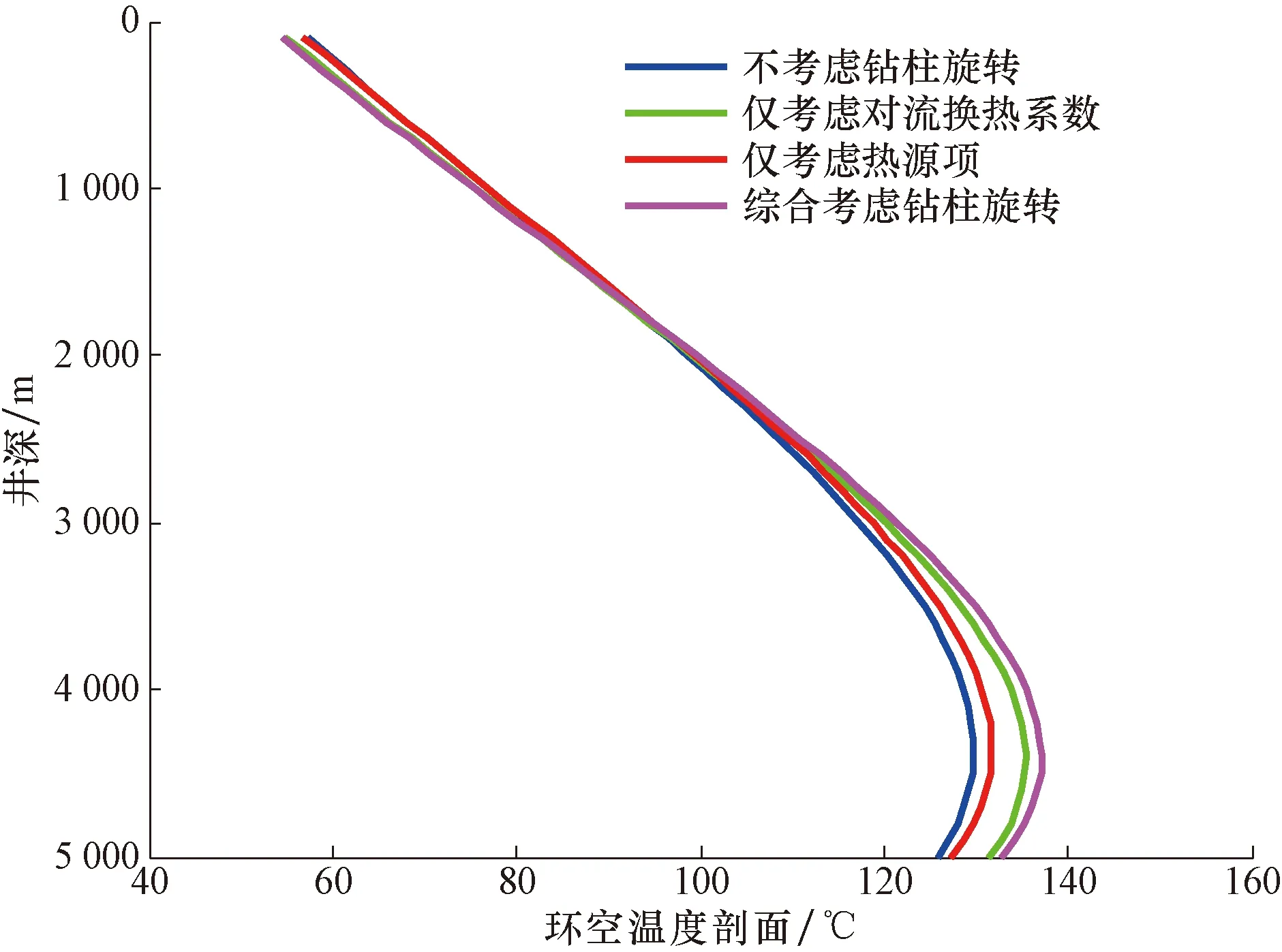
图7 考虑钻柱旋转和不考虑钻柱旋转时的环空温度剖面Fig.7 Annular temperature profile with or without considering drill string rotation

4 工程应用

4.1 温度对井底压力的影响

基于以上温度场模型及分析，结合高温高压条件下循环当量密度计算模型[18]，可确定温度场对井底压力的影响。新疆某区块采用密度为1.8 kg/L的油基钻井液进行钻进，仅考虑地层温度计算出的井底压力比使用文中模型计算的结果小1.0 MPa；不考虑温度压力影响时，计算出的井底压力比使用文中模型计算的结果大1.1 MPa。因此，无论是不考虑温度压力影响还是只考虑地层温度的影响，其计算结果都与文中模型的计算结果相差1.0 MPa左右。因此，在正常钻进过程中，考虑非牛顿流体螺旋流动对井筒循环温度场的影响对于窄钻井液密度窗口地层的压力计算至关重要，其影响不可忽略。

4.2 基于温度场模型的井筒温度控制

在深井钻进高温地层过程中，温度过高会导致井下测量仪器与导向仪器失效，井下信号无法传输，温度过高还会影响钻井液的稳定性。因此，温度的控制对于钻井安全至关重要。基于上文所建温度场模型分析可采用以下方法降低井底温度：1)在保证钻井液性能的情况下，适当增大钻井液的比热容；2)在保证钻井作业正常进行的情况下，适当降低钻柱的转速；3)降低钻杆入口处钻井液的温度。

此外，由以上分析可知，随着井深的增深，钻柱旋转对井底温度的影响更加明显。在深井采用螺杆复合钻进时，近钻头处钻柱转速在200 r/min以上，大大加大了地层与井筒的热量交换，此时应特别注意由钻柱旋转所引起的温度变化。

5 结 论

1) 根据非牛顿流体螺旋流动的特点，综合考虑热源项和钻柱旋转对井底循环温度的影响，建立了钻井过程中井筒与地层的温度场模型，并通过现场试验验证了模型的可靠性。

2) 钻柱旋转一方面增大了黏性耗散的热量，另一方面增大了井筒与地层的对流换热系数，使井底温度上升，其中由钻柱旋转导致的对流换热系数的增大占主要作用。

3) 井底温度随钻柱转速的升高呈指数增长；随着井深的增深，钻柱旋转对井底温度的影响更加明显，在深井钻井井筒循环温度场的计算过程中，不能忽略钻柱旋转对井筒温度分布的影响。

参考文献
References

[1] Holmes C S,Swift S C.Calculation of circulating mud temperature[J].Journal of Petroleum Technology,1970,22(6):670-674.

[2] Kabir C S,Hasan A R,Kouba G E,et al.Determining circulating fluid temperature in drilling,workover and well control operations[J].SPE Drilling & Completion,1992,11(2):74-79.

[3] 何世明，何平，尹成，等.井下循环温度模型及其敏感性分析[J].西南石油学院学报，2002,24(1)：57-60.

He Shiming,He Ping,Yin Cheng,et al.A wellbore temperature model & it’s parametric sensitivity analysis[J].Journal of Southwest Petroleum Institute,2002,24(1):57-60.

[4] 易灿，闫振来，郭磊.井下循环温度及其影响因素的数值模拟研究[J].石油钻探技术，2007,35(6)：47-49.

Yi Can,Yan Zhenlai,Guo Lei.Numerical simulation of circulating temperature and it’s impacting parameters[J].Petroleum Drilling Techniques,2007,35(6):47-49.

[5] 窦亮彬，李根生，沈忠厚，等.注CO2井筒温度压力预测模型及影响因素研究[J].石油钻探技术，2013,41(1)：76-81.

Dou Liangbin,Li Gensheng,Shen Zhonghou,et al.Wellbore pressure and temperature prediction model and its affecting factors for CO2injection wells[J].Petroleum Drilling Techniques,2013,41(1):76-81.

[6] Thompson M,Burgess T M.The prediction of interpretation of mud temperature while drilling[R].SPE 14180,1985.

[7] Osisanya S O,Harris O O.Evaluation of equivalent circulating density of drilling fluids under high-pressure/high-temperature conditions[R].SPE 97018,2005.

[8] Gonzalez M E,Bloys J B,Lofton J E,et al.Increasing effective fracture gradients by managing wellbore temperatures[R].IADC/SPE 87217,2004.

[9] Iyoho A W,Rask J H,Wieseneck J B,et al.Comprehensive drilling model analyzes BHT parameters[R].SPE 124142,2009.

[10] 高德利.油气井管柱力学与工程[M].东营：中国石油大学出版社，2006:88-89.

Gao Deli.Mechanics and engineering string of oil and gas wells[M].Dongying:China University of Petroleum Press,2006:88-89.

[11] Ahmed R M,Enfis M S,Kheir H M E,et al.The effect of drillstring rotation on equivalent circulation density:modeling and analysis of field measurements[R].SPE 135587,2010.

[12] Fénot M,Bertin Y,Dorignac E,et al.A review of heat transfer between concentric rotating cylinders with or without axial flow[J].International Journal of Thermal Sciences,2011,50(7):1138-1155.

[13] 崔海清，刘希圣.非牛顿流体偏心环形空间螺旋流的速度分布[J].石油学报，1996,17(2)：76-83.

Cui Haiqing,Liu Xisheng.Velocity distribution of helical flow of non-Newtonian fluid in eccentric annuli[J].Acta Petrolei Sinica,1996,17(2):76-83.

[14] Gazley C.Heat transfer characteristics of the rotational and axial flow between concentric cylinders[J].Journal of Heat Transfer,1958,80(1):79-90.

[15] Marshall D W,Bentsen R G.A computer model to determine the temperature distributions in a wellbore[J].Journal of Canadian Petroleum Technology,1982,21(1):63-75.

[16] 陶文铨.数值传热学[M].西安：西安交通大学出版社，1988:85.

Tao Wenquan.Numerical heat transfer[M].Xi’an:Xi’an Jiaotong University Press,1988:85.

[17] 张涛，柳贡慧，李军，等.随钻压力测量系统的研制与现场试验[J].石油钻采工艺，2012,34(2)：20-22.

Zhang Tao,Liu Gonghui,Li Jun,et al.Pressure while drilling system development and field test[J].Oil Drilling & Production Technology,2012,34(2):20-22.

[18] 罗宇维，朱江林，李东，等.温度和压力对井内流体密度的影响[J].石油钻探技术，2012,40(2)：30-34.

Luo Yuwei,Zhu Jianglin,Li Dong,et al.The impact of temperature & pressure on borehole fluids density[J].Petroleum Drilling Techniques,2012,40(2):30-34.