基于排列熵和VPMCD的滚动轴承故障诊断方法

程军圣，马兴伟，杨 宇

(湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082)

机械故障诊断过程本质上是一个故障模式识别的过程[1]，针对某一具体的机械故障诊断问题，选择不同的模式识别方法，其分类精度和准确性可能会有较大的差异[2-3]。神经网络结构和类型的选择过分依赖于先验知识或经验，而这将会影响其分类精度[4]。支持向量机分类结果受到核函数及其参数的影响。此外，其搜索算法本质上是二进制的，对于多类分类问题则需要进行多次的二进分类[5]。

熵不但能表征信号的复杂性，而且能够度量一个系统或一段信息的不确定性，因而有利于处理非线性问题。排列熵(Permutation Entropy，简称PE)算法是由Bandt等[13]最近提出的一种新的检测时间序列随机性和动力学突变的方法。Yan等[14]将其应用于旋转机械振动信号的特征提取，并将排列熵与近似熵和Lempel-Ziv复杂度进行了对比，结果表明，排列熵算法能够有效地检测和放大振动信号的动态变化，表征滚动轴承在不同状态下的工况特征。

本征时间尺度分解(Intrinsic Time-scale Decomposition，简称ITD)是由Frei等[15]提出的一种自适应时频分析方法，该方法能将非平稳信号分解成为若干瞬时频率具有物理意义的合理旋转(Proper Rotation，简称PR)分量。与EMD相比，ITD在端点效应和计算速度上都有明显优势[16]，且可以避免EMD方法中的包络误差。

论文将排列熵和VPMCD方法相结合应用于滚动轴承故障诊断，利用ITD方法对原始信号进行分解得到若干固有旋转分量，提取各个分量的排列熵并将其作为特征值，进一步采用VPMCD方法进行故障诊断。将VPMCD方法与BP(Back Propagation)神经网络以及支持向量机(Support Vector Machine，简称SVM)进行了实验对比分析，结果表明，VPMCD方法可以有效地应用于滚动轴承故障诊断。

1 VPMCD方法

在VPMCD方法中，为特征值Xi定义的变量预测模型VPMi为一个线形或非线性的回归模型，可以选择以下的模型之一：

① 线性模型(L):

高校图书馆的特色资源是高校资源的优势所在，越来越凸显其不可替代的核心作用，并俨然成为图书馆核心竞争力的重要指标。特色资源为教学科研以及专业人才培养提供了有力的资源保障。

(1)

② 线性交互模型(LI)：

(2)

③ 二次交互模型(QI)：

(3)

④ 二次模型(Q)：

(4)

式中，r≤p-1为模型阶数。以p个特征值问题为例，以上述四种模型中任意一个模型，采用特征值Xj(j≠i)对Xi进行预测，都可以得到：

Xi=f(Xj,b0,bj,bjj,bjk)+e

(5)

式(5)称为特征值Xi的变量预测模型VPMi。其中，特征值Xi称为被预测变量；Xj(j≠i)称为预测变量；e为预测误差；b0,bj,bjj,bjk为模型参数，他们可以通过训练样本数据对预测模型进行训练得到，这其实是采用所有训练样本的特征值X=[X1,X2,…,Xp]对b0,bj,bjj,bjk等模型参数进行估计的问题。

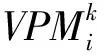
在VPMCD方法中，采用同一类别下所有特征值的预测误差平方和值最小为判别函数对测试样本进行分类，因此该方法可以有效地应用于具有多种样本的模式识别。

2 排列熵参数的选择

排列熵算法不考虑数据具体值，而是基于相邻数据的对比对数据进行分析，因此计算简洁、速度快，抗干扰能力强，特别适用于非线性数据，具有很好的鲁棒性，对噪声有很好的抑制作用[13]。

在排列熵的计算中，有三个参数值需要考虑和设定，即时间序列长度N，嵌入维数m和时延τ。Bandt等[13]建议，嵌入维数m的取值为3～7，因为如果m等于1或2，此时重构的向量中包含太少的状态，算法失去意义和有效性，不能检测时间序列的动力学突变。但是，如果m取值过大，也不合适，因为相空间的重构将会均匀化时间序列，此时不仅计算比较耗时，而且也无法反映序列的细微变化[17-18]。

时延τ对时间序列的计算影响较小，以长度为1 024的随机信号为例，在不同τ下的排列熵值随嵌入维数的变化关系如图1所示，由图1可以看出，时延τ对信号熵值的影响较小，因此，论文中均取τ=1。

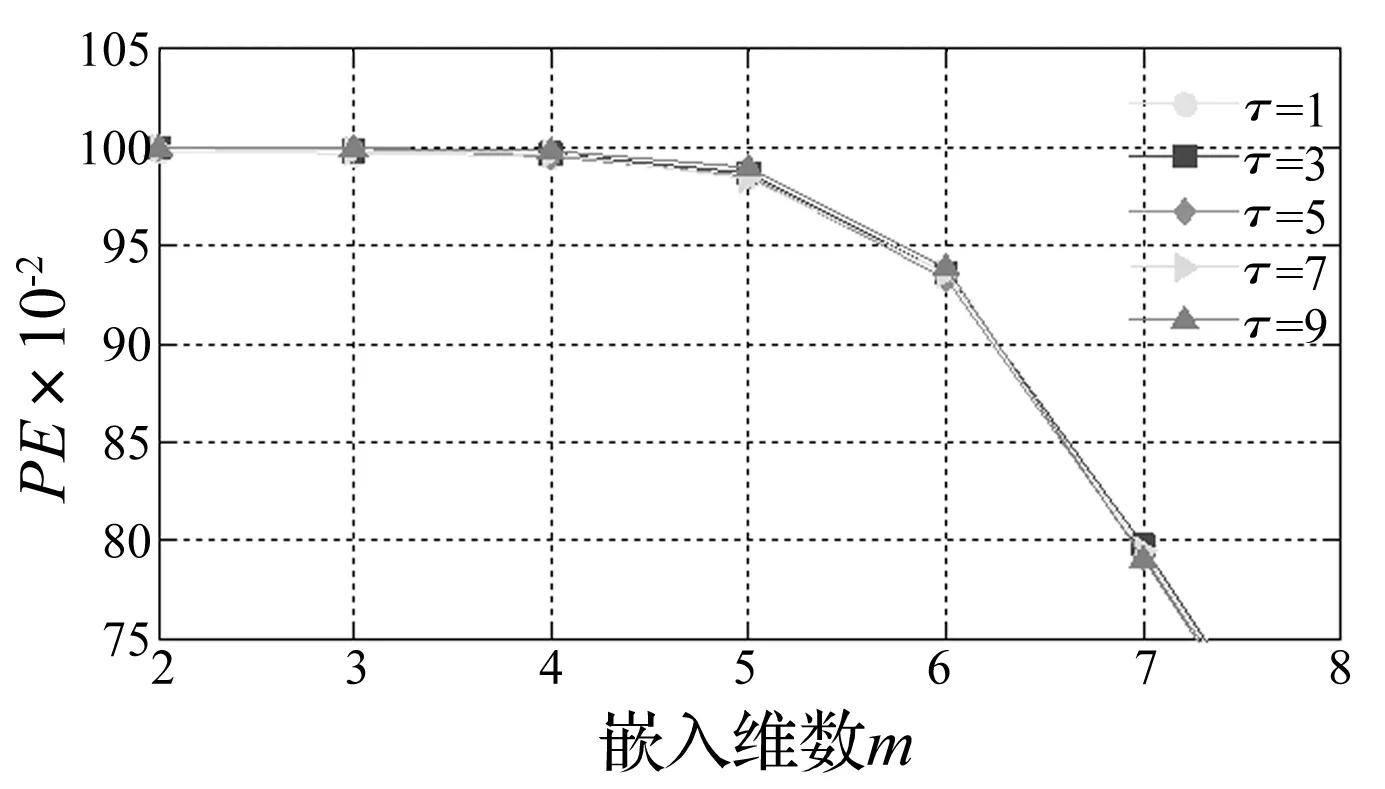
图1 随机信号在不同时延下的排列熵

为研究数据长度N对排列熵值的影响，论文取时延τ=1，以长度分别为256，512，1 024，2 048的随机信号为例，求得对应排列熵值，分别记为PE1，PE2，PE3，PE4，如图2所示，它们在不同嵌入维数下差值如表1所示。

由图2和表1可知，当m=5，τ=1时，数据长度为1 024与长度512，熵值相差0.017 8，而与长度2 048熵值相差0.006 4，因此，此时选数据长度为1 024较合适。一般，嵌入维数较小时，数据长度则要求越小。论文中，嵌入维数m=5，时延τ=1，数据长度N=1 024。

图2 不同长度的随机信号的排列熵

表1 不同长度的随机信号排列熵在不同嵌入维数下的差值

3 基于排列熵和VPMCD的滚动轴承故障诊断步骤

对原始振动加速度信号进行ITD分解(具体算法见文献[15])，提取各个PR分量的排列熵作为特征值并构建特征值向量，结合VPMCD分类器进行模式识别。具体步骤如下：

① 分别在滚动轴承正常状态、外圈故障、内圈故障、滚动体故障状态下，按照一定的采样频率f进行N次重采样，共获得4N个振动加速度信号作为训练样本。

② 对滚动轴承四种状态下的每一个振动加速度信号进行ITD分解，得到若干个PR分量，选择前m个含有故障信息的PR分量作为研究对象。

③ 对含有故障信息的前m个PR分量分别提取排列熵Xi(i=1,2,…,m)，并构建特征值向量X=[X1,X2,…,Xm]。

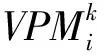
⑤采集测试信号。按照步骤①、②、③构建测试样本特征值向量X′，并将其作为VPMCD分类器的输入，以VPMCD分类器的输出来确定滚动轴承的工作状态和故障类型。

4 实验分析

机械设备在运行时，其关键零部件滚动轴承可能会出现内圈故障、外圈故障或滚动体故障。为验证排列熵和VPMCD方法的有效性，采用美国凯斯西储大学电气工程实验室的滚动轴承数据[19]，选用的滚动轴承为6205-2RS JEM SKF型深沟球轴承，采样频率为12 kHz，电机负载为0 HP，转速为1 797 r/min。故障点的直径为0.177 8 mm，故障深度为0.279 4 mm。图3为采集到的滚动轴承故障振动加速度信号：

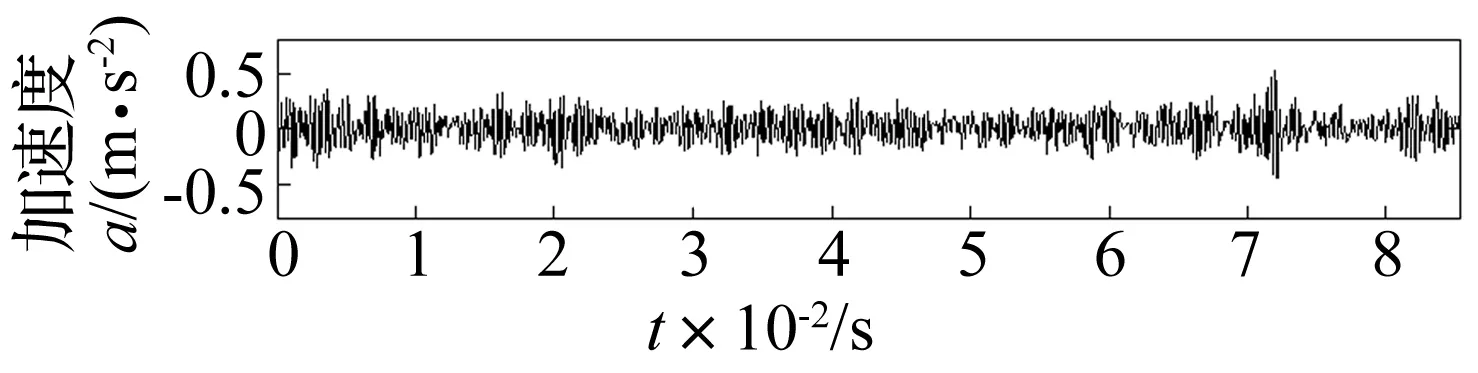
图3 滚动轴承滚动体故障状态下的振动加速度信号

对图3滚动轴承滚动体故障状态下的振动加速度信号进行ITD分解，得到的各个PR分量如下图4所示：

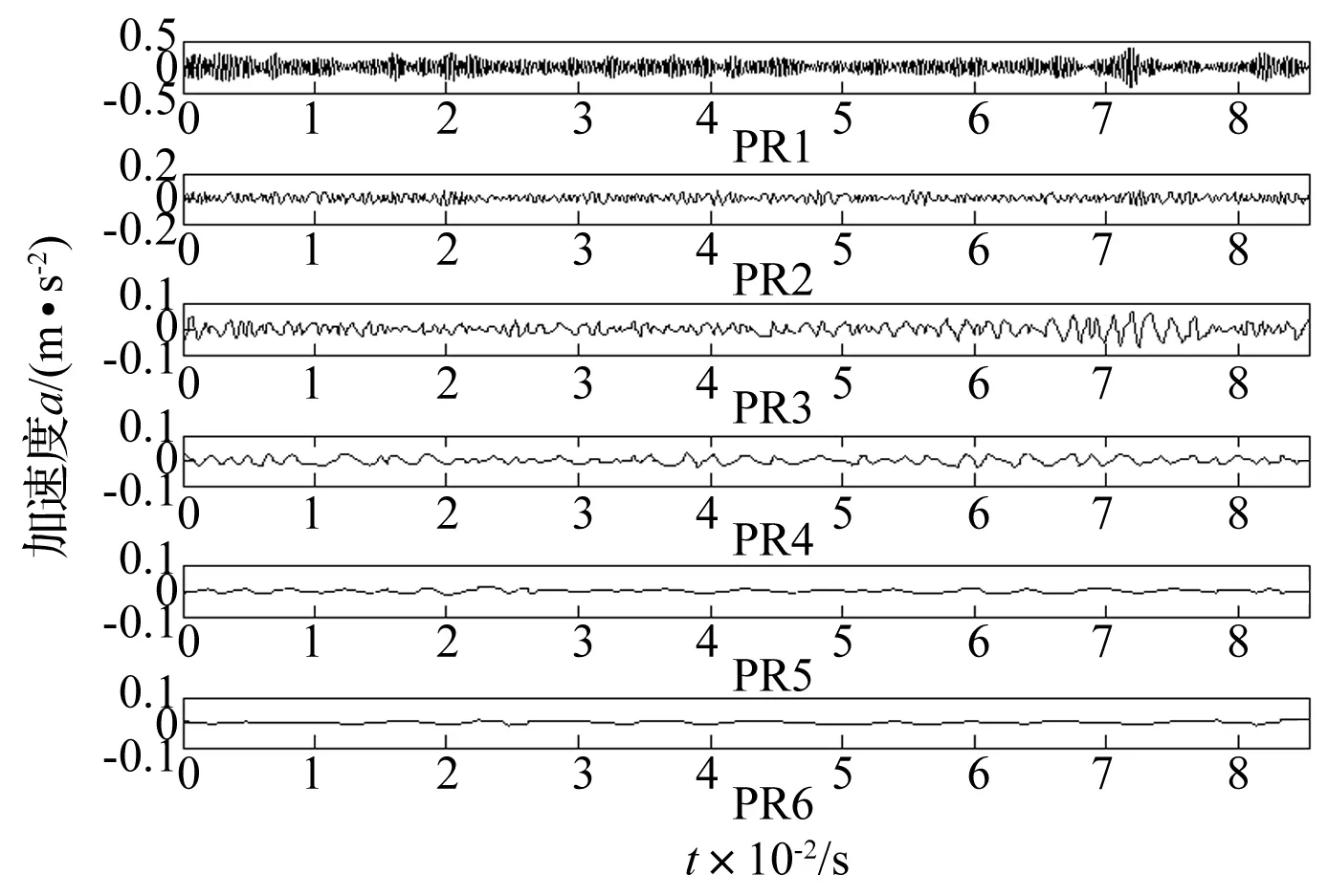
图4 滚动轴承滚动体故障状态下的振动信号的ITD分解结果

ITD是将信号分解为从高到低不同频率段的单分量信号，滚动轴承故障振动信号的故障信息主要集中在高频段。由图4可知，滚动轴承的主要故障信息集中在前4个PR分量，故论文中选取了前4个PR分量提取排列熵并结合VPMCD方法进行故障诊断。

论文选取滚动轴承正常状态下的振动信号200组数据，外圈故障、内圈故障、滚动体故障三类状态下的振动信号各110组数据。在正常样本数据中随机抽取100组数据，其余三类故障样本数据中各随机抽取60组数据作为训练样本数据，将剩下的100组正常样本数据和外圈故障、内圈故障、滚动体故障三类故障状态下各50组数据作为测试样本。

首先，对训练样本数据进行ITD分解，对每一组样本数据分解后的前4个PR分量分别提取排列熵，形成排列熵特征值向量。将特征值向量输入到VPMCD分类器中对其进行训练。

其次，将正常状态下剩余的100组测试样本和其余三类状态剩余的各50组数据按照上述同样的方法提取排列熵特征值向量，输入到已经训练好的VPMCD分类器中进行模式识别。

VPMCD方法利用训练样本估计模型参数，建立变量预测模型VPMk(k=1,2,3,4时，分别对应为正常、滚动体故障、内圈故障、外圈故障样本的预测模型)，从而对测试样本的故障类型分类。对滚动轴承四种状态共250组测试样本用训练好的VPMCD分类器进行分类，识别率达100%。表2给出了四组测试样本的诊断结果。

为研究VPMCD方法在估计模型参数时，样本数量的选取问题，论文选取上述美国凯斯西储大学滚动轴承正常状态、外圈故障、内圈故障、滚动体故障四类状态下的振动信号各110组数据。在正常样本和其余三类故障样本数据中各随机抽取20、40、50、60、80组数据作为训练样本数据，将剩下的样本数据作为测试样本。表3给出了在不同训练样本数情况下VPMCD分类器的分类结果。

表2 基于排列熵与VPMCD的滚动轴承故障识别结果

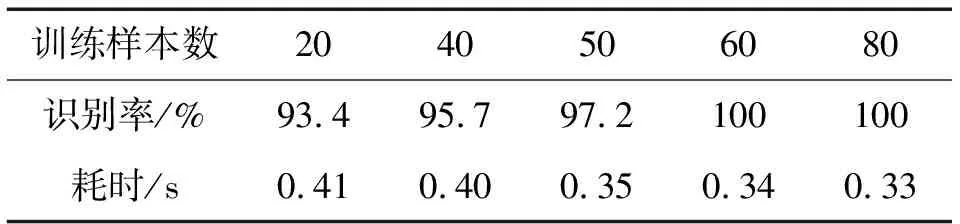
表3 不同训练样本数下VPMCD分类器识别结果

由表3可知，当训练样本数超过60，VPMCD分类器分类精度可达100%。在模式识别中，样本数量并不是与分类精度成正比的。而且训练样本数量增多，运算时间也会增加。因此，针对上述西储大学滚动轴承数据，VPMCD分类器在估计模型参数时，样本数量可根据表3进行选取。

为比较VPMCD方法和常用神经网络和支持向量机的识别效果，论文同样选取上述美国凯斯西储大学滚动轴承正常状态、外圈故障、内圈故障、滚动体故障四类状态下的振动信号各110组数据。在正常样本和其余三类故障样本数据中各随机抽取60、80组数据作为训练样本数据，分别对SVM、BP神经网络和VPMCD进行训练，将剩下的样本数据作为测试样本，并将三类分类器的识别结果进行对比分析，如表4所示。

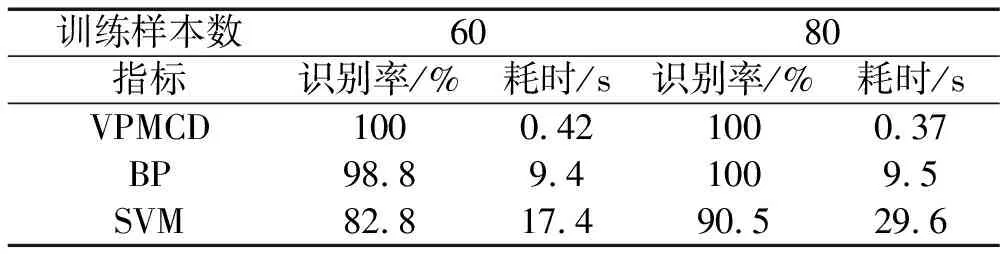
表4 VPMCD、BP和SVM识别结果对比

由表4可知采用不同数量的训练样本对VPMCD、BP神经网络和SVM分别进行训练后，各分类器识别率均较高，说明排列熵算法能够有效地检测和放大振动信号的动态变化，表征滚动轴承在不同状态下的工况特征。同时，VPMCD分类器的训练、测试时间要比BP神经网络和SVM短，说明VPMCD方法不仅避免了神经网络的迭代学习而且避免了SVM的寻优过程以及SVM对于多类分类问题需要进行多次的二进分类问题，大大减少了运算量。在使用BP神经网络时还发现，误差指标如果过小还会出现过学习现象。另外，BP神经网络和SVM需要进行严格的结构参数的优化选择才能达到较高的识别率，而VPMCD分类器无需进行结构参数的优化选择。由表4也可看出当训练样本较少时，VPMCD分类器仍然能达到较高的识别率。在实际工程应用中可用的故障特征信号是比较缺乏的，显然VPMCD方法更适用于实际的滚动轴承故障诊断和状态监测。

5 结 论

本文提出了一种基于排列熵和VPMCD的滚动轴承故障诊断方法。排列熵算法用来检测时间序列的动力学突变，但由于机械系统的复杂性，振动信号表现不同尺度的动力学突变，基于此，本文提出用ITD方法将振动信号进行多尺度分解，提取排列熵特征值向量，然后进行VPMCD模式识别，根据VPMCD模式识别结果判断滚动轴承的工作状态。通过分析得到如下结论：

(1) 从原始数据中提取的特征值实际上反映了原始数据的本质特征，VPMCD方法依据特征值之间的相互内在关系建立预测模型，避免了神经网络的迭代学习和支持向量机的寻优过程，能更有效地实现分类。

(2) VPMCD方法采用各类样本数据对预测模型参数进行估计，从而得到不同类别的预测模型，然后，采用预测模型对测试样本进行分类。实验分析结果表明，VPMCD方法在训练样本数较少也能有效地对预测模型参数进行估计。

(3) 在训练样本数不同的情况下将VPMCD与BP、SVM相比，分析结果表明VPMCD能更有效地识别滚动轴承故障的特征信息。VPMCD方法避免了神经网络结构和类型的选择、支持向量机核函数及其参数的选择依靠先验知识或经验问题，同时避免了支持向量机的二进分类问题，可以同时进行多类分类。

(4) 排列熵算法是一种新的检测时间序列随机性和动力学突变的方法，具有计算简单、快速，抗噪能力强，适合在线监测等优点。将排列熵和VPMCD方法引入滚动轴承故障诊断中，结果表明了该方法可以有效地识别滚动轴承的工作状态。

[1]温熙森.模式识别与状态监控[M].北京:科学出版社,2007.

[2]LEI Ya-guo，HE Zheng-jia，ZI Yan-yang，et al. New clustering algorithm-based fault diagnosis using compensation distance evaluation technique [J].Mechanical Systems and Signal Processing, 2008,22(2):419-435.

[3]Rafiee J, Tse P W，Harifi A，et al. A novel technique for selecting mother wavelet function using an intelligent fault diagnosis system [J].Expert System with Applications, 2009, 36(3):4862-4875.

[4]Wang C C，Kang Y，Shen P C，et al. Applications of fault diagnosis in rotating machinery by using time series analysis with neural network[J].Expert System With Application, 2010,37(2):1696-1702.

[5]FEI Sheng-wei，ZHANG Xiao-bin.Fault diagnosis of power transformer based on support vector machine with genetic algorithm[J]. Expert Systems with Application, 2009, 36(8):11352-11357.

[6]Raghuraj R，Lakshminarayanan S. Variable predictive models-A new multivariate classification approach for pattern recognition applications[J].Pattern Recognition, 2009, 42(1):7-16.

[7]Raghuraj R,Lakshminarayanan S.Variable predictive model based classification algorithm for effective separation of protein structural classes[J].Computational Biology and Chemistry, 2008,32(4):302-306.

[8]Raghuraj R，Lakshminarayanan S.VPMCD:Variable interaction modeling approach for class discrimination in biological system[J].FEBS Letter,2007,581(5):826-830.

[9]Wang X Y，Makis V，Yang M. A wavelet approach to fault diagnosis of a gearbox under varying load conditions[J].Journal of Sound and Vibration,2010,329(9):1570-1585.

[10]Kankar P K，Sharma S C，Harsha S P. Fault diagnosis of ball bearing using continuous wavelet transform[J]. Applied Soft Computing, 2011, 11(2):2300-2312.

[11]WU Fang-ji，QU Liang-sheng.Diagnosis of subharmonic faults of large rotating machinery based on EMD[J].Mechanical Systems and Signal Processing,2009,23(2):467-475.

[12]CHENG Jun-sheng,YANG Yu,YU De-jie.The envelope order spectrum based on generalized demodulation time-frequency analysis and its application to gear fault diagnosis[J]. Mechanical System and Signal Processing,2010,24(2):508-521.

[13]Bandt C, Pompe B. Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, The American Physiological Society，2002，88(17)：174102(1-4).

[14]Yan R Q，Liu Y B，Gao R X. Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines[J]. Mech. Syst. Signal Process, 2012 (29): 474-484.

[15]Frei M G, Osorio I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society. A, 2007, 463: 321-342.

[16]安金坤，田斌，孙永军，等.一种基于ITD算法的直扩信号检测算法[J].电子与信息学报,2010,32(5):1178-1182.

AN Jin-kun，TIAN Bin，SUN Yong-jun，et al. An algorithm for direct sequence spread spectrum signal detection based on intrinsic time-scale decomposition[J]. Journal of Electronics & Information Technology, 2010,32(5):1178-1182.

[17]Yan R Q，Gao R X. Approximate entropy as a diagnostic tool for machine health monitoring[J]. Mechanical Systems and Signal Process, 2007，21 (2) 824-839.

[18]Cao Y，Tung W W, Gao J B, et al. Detecting dynamical changes in time series using the permutation entropy[J]. Phys. Rev, 2004 (E70) 046217.

[19]Case Western Reserve University Bearing Data Center. Bearing data center fault test data. [EB/OL].[2012-11-10]. http://www.eecs.case.edu/laboratory/bearing.