冲击荷载作用下混凝土缺陷模型细观损伤演化定量分析

覃 源，柴军瑞,2，党发宁

(1．西安理工大学 陕西省西北旱区生态水利工程重点实验室，西安 710048；2．三峡大学 土木水电学院，湖北 宜昌 443002)

混凝土是常见的工程材料，主要由人工或者机器搅拌而成，其细观结构存在天然的裂缝、孔洞是不可避免的，这些裂缝和孔洞可以看作是混凝土材料内部固有的缺陷。很多学者对混凝土材料开展了大量研究，他们所采用的研究方法大致分为两种：物理试验法和数值模拟法。

试验方面，人们对混凝土材料细观缺陷进行无损检测. Cheng等[1]将红外热量图示测量法与弹性波相结合，成功探测了混凝土材料内部细观结构的缺陷。丁卫华等[2-3]将便携式加载设备与CT技术相结合，研制出与医用CT机配套的混凝土实时加载扫描设备，得到了材料内部细观缺陷的分布状况。数值模拟方面，郑丹等[4]提出了基于静力本构和细观缺陷的混凝土动力本构模型，Wu等[5]建立了带有外部缺陷(人工切割的凹槽)的混凝土梁模型，分析了混凝土梁的动力断裂韧性。

由于混凝土材料细观结构随机性强，所以物理试验结果随机性较大，可重复性低，在冲击荷载作用下试件细观结构的变化特点更难得到；而大部分数值试验，主要偏向于研究无缺陷或存在外部缺陷的混凝土试件，而对含有内部缺陷的混凝土试件在冲击荷载作用下力学特性的研究较少。

本文通过改进传统的建模方法，实现了混凝土材料内部缺陷化处理，建立了含有细观缺陷的混凝土随机骨料模型。并将缺陷单元进行分区，分析了不同速率冲击荷载作用下，内部缺陷对混凝土材料细观损伤的影响，总结了细观损伤发展对宏观裂纹演化的影响规律。

1 材料内部缺陷的建立

数值试验中混凝土试件尺寸、分析区域尺寸及边界条件如图1，材料参数和加载速率分别如表1和表2。

表1 材料参数表

表2 加载速率表

由于混凝土是一种准脆性材料，荷载作用下细观裂缝的产生和发展是导致混凝土试件宏观应力-应变曲线非线性的重要因素，所以可以采用弹性损伤本构模型来描述其受力开裂过程。该模型通过材料弹性模量的折减度和损伤变量D(D=0无损伤，D=1完全损伤)来反映混凝土试件的细观损伤，损伤变量D与材料弹性模量的退化密切相关，应力-应变关系可以表达为：

(1)

(2)

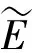
(3)

其中ε0为单元抗拉强度达到抗拉强度ft时对应的主应变，残余抗拉强度可表示为：

ftr=λ·ft(0<λ≤1)

(4)

其中λ为残余抗拉强度系数，εr为单元抗拉强度达到残余抗拉强度ftr时的残余应变，表示为：

εr=η·ε0(0<η≤5)

(5)

其中η为残余应变系数。εu为单元的极限拉应变，由式(6)确定：

εu=ξ·ε0(ξ>η)

(6)

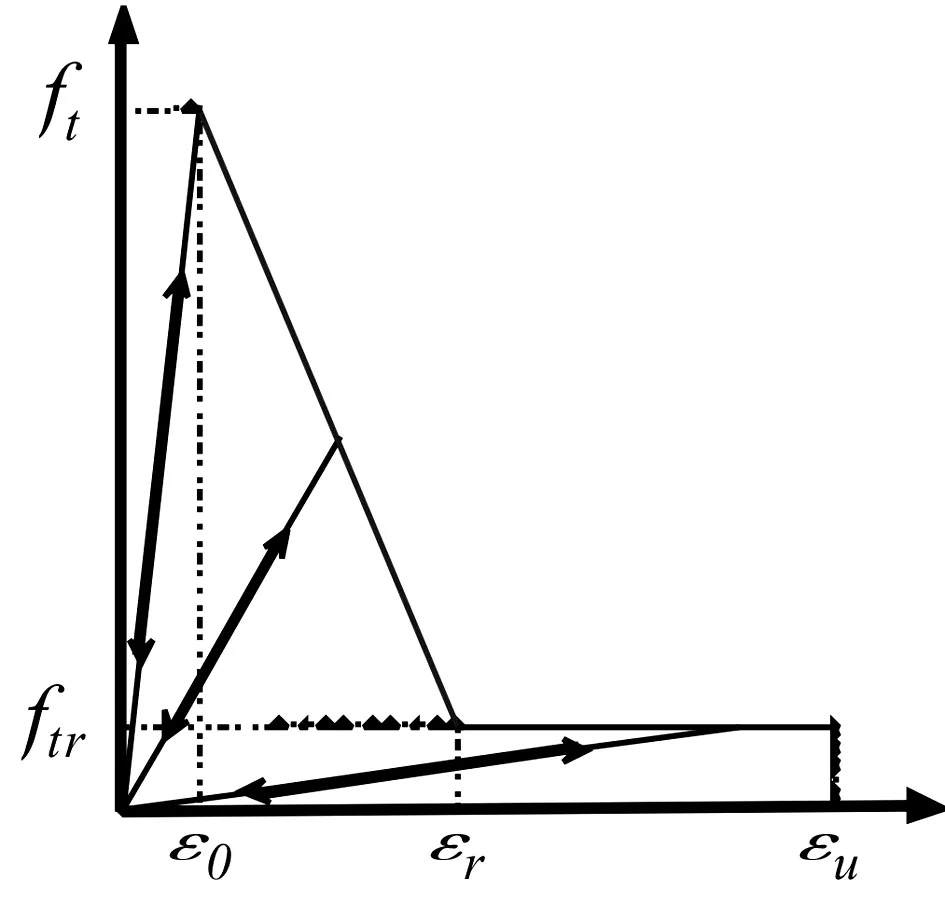
图2 双折线损伤演化模型

其中ξ为极限拉应变系数，εmax为加载时某一荷载值对应的最大拉应变值，εmax会随着荷载的变化而变化。如图2，当εmax<ε0时，单元处于弹性阶段，此阶段内无单元发生损伤；当ε0<εmax≤εr时，一部分单元发生第一阶段的损伤，而当εr<εmax≤εu时，除了第一阶段损伤单元之外，又产生了第二阶段损伤单元，值得注意的是，处于第二阶段损伤的单元中，有相当一部分单元是在第一阶段损伤基础上产生的。而另外有一部分单元则未产生第一阶段损伤，直接产生了第二阶段的损伤，可见第一和第二阶段损伤既相互联系又相互区别。当εmax>εu时，单元完全破坏。

建立混凝土缺陷模型的具体流程如图3，每个步骤的具体解释如下。

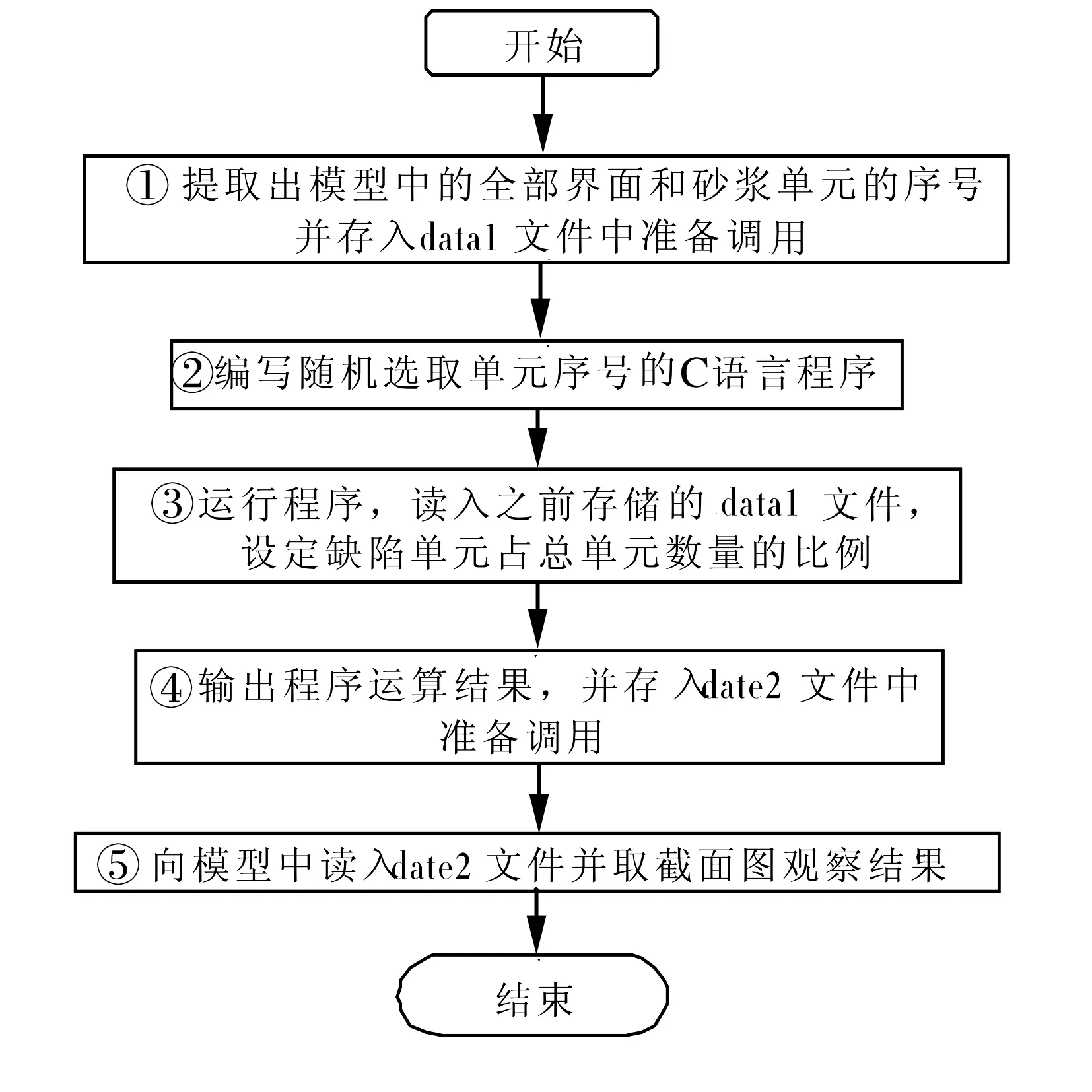
图3 混凝土缺陷模型建模流程

①提取出细观分析区域所有界面和砂浆单元，存入data1文件中，在这里需要统计出具体的骨料、界面和砂浆单元的数量以备之后的程序运行使用，模型Ⅰ中以上三者的单元总数为235 630个，其中骨料单元38 481个，界面单元107 137个，砂浆单元90 012个。

②用C语言编写程序，目的是为了从以上的界面和砂浆单元当中选出指定数量的单元进行缺陷化处理。

③运行程序之前需设定好缺陷单元占总单元数的比例，假设缺陷单元数量占界面和砂浆单元数量的1%，即缺陷单元数量为1 971.49个，取整数为1 971个，将这些缺陷单元平均分配到试件三个分区上(分区如图4)，那么每个分区有657个缺陷单元，定义缺陷单元弹性模量为1.5×107Pa，泊松比为0.14，颜色为浅灰色，然后再读入之前存储的data1文件。

④运行自编程序时，将输出语句统一编写为ANSYS命令流形式“MAT,n”，其中MAT为material的缩写，n代表材料属性(在这里代表缺陷单元的材料属性)，将程序运行结果统一保存到data2文件中。

⑤将上一步得到的data2文件直接读入模型中，然后列表查看整体单元数量是否发生变化，若整体单元数量仍为235 630个，说明之前的步骤中没有出现错误，该模型可以使用，若出现总单元数量少于235 630个时，应及时检查上一步的输出结果是否包含了所有选中的单元。在核对模型正确性之后，取其截面图进行结果观察，如图4。

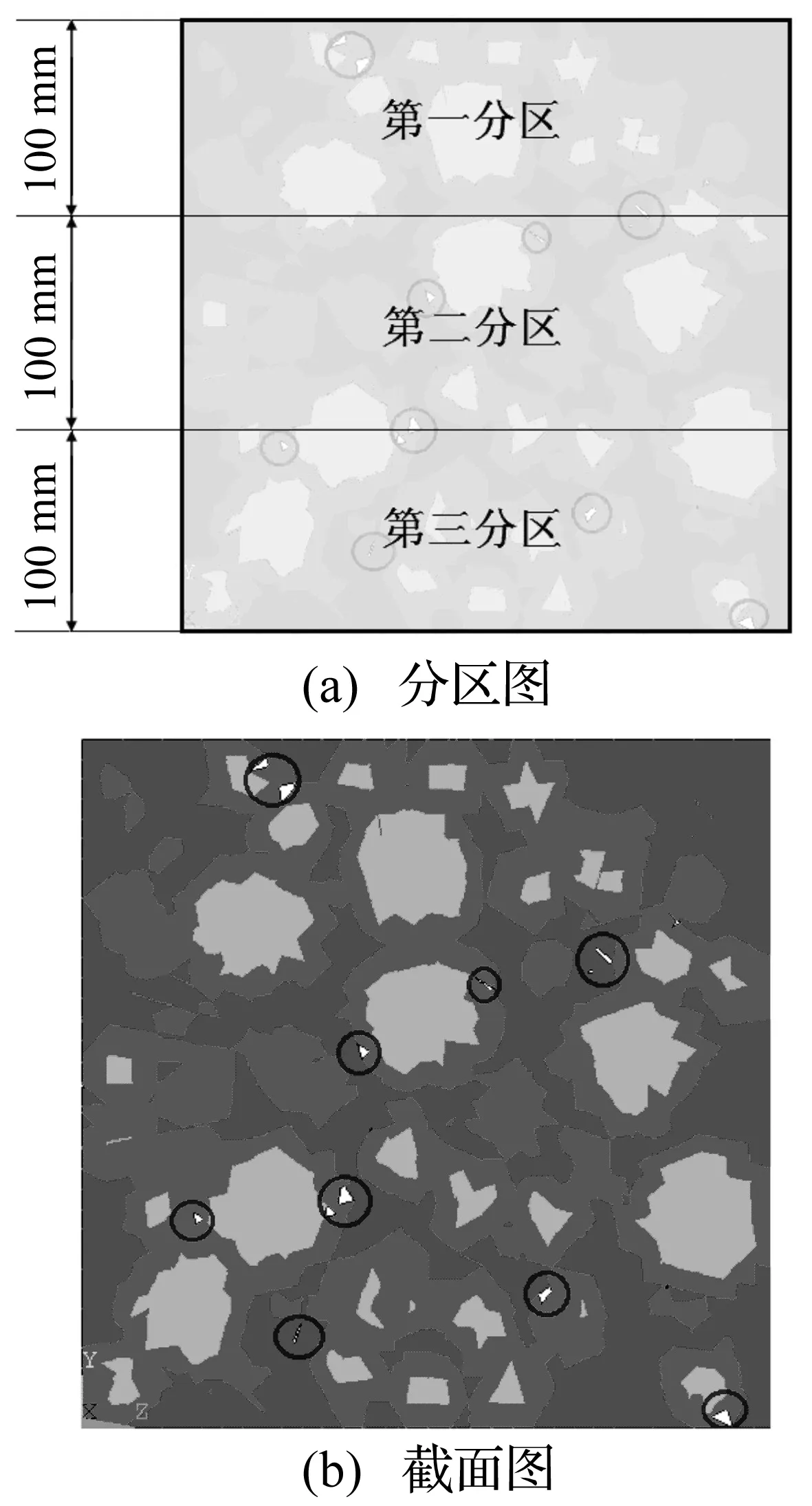
图4 混凝土缺陷模型

至此，带有分区缺陷单元的数字混凝土模型建立完毕，在分析讨论中，称这种带有内部缺陷的混凝土模型为“混凝土缺陷模型”或“缺陷模型”。

2 混凝土缺陷模型数值试验分析

2.1 混凝土缺陷模型的损伤与破坏

表3为混凝土缺陷模型损伤和破坏截面图。从中看出，加载初期(第9荷载步)在不同速率冲击荷载作用下，第三分区产生了一定数量的损伤单元(杂色斑块)和少量的破坏单元(白色斑块)，分布在第三分区以外区域的缺陷单元并未受到外荷载带来的影响，而处于第三分区的缺陷单元受到来自外荷载作用以及周围微裂纹的影响较大，一些邻近的缺陷单元相互接触形成了更大的内部缺陷；一些较大的缺陷单元吸收了附近较小的缺陷单元，成为了细观微裂纹的组成部分。随着冲击荷载速率的增加，该现象变得逐渐明显。

加载中期(第17荷载步)，第三分区的损伤和破坏单元数量显著增加，同时出现了数量较多的细观微裂纹，此时第二分区的部分缺陷单元也受到了来自冲击荷载的影响，一部分单元发生了破坏并与缺陷单元相接触，产生了少量细观微裂纹，冲击速率越快，相同荷载步内裂纹接触缺陷单元的数量越多，试件损伤越严重。

加载末期(第25荷载步)，第一分区也出现了少量的损伤和破坏单元。第二分区中，损伤和破坏单元从分区底部向中部发展，经过统计数量明显超过第一分区，这些损伤和破坏单元在发展过程中与缺陷单元相接触，形成明显的裂纹。第三分区中存在的裂纹大都以宏观裂纹为主，较细观微裂纹而言，宏观裂纹体积更大，穿透力和破坏力更强，所以吸收缺陷单元的能力也更强，靠近宏观裂纹的缺陷单元几乎全部加入宏观裂纹当中。然而虽然有相当数量的缺陷单元加入到了宏观裂纹当中，裂纹发展趋势受缺陷单元的影响不如之前荷载步显著，主要表现为，在加载中期以前，细观微裂纹会追随大体积缺陷单元的位置发展，而在加载末期，宏观裂纹只吸收附近缺陷单元，并不会因为缺陷单元的存在而改变总体的发展方向。说明随着荷载的增加，宏观裂纹的增多，内部缺陷对试件的损伤和破坏的影响力逐渐降低。

2.2 混凝土缺陷模型应力分布

混凝土缺陷模型在加载过程中的水平向应力分布如表4。加载初期，第三分区缺陷单元周围产生了较为明显的拉应力集中现象，由于此时破坏单元数量较少，部分应力选择较为薄弱的缺陷单元进行释放，这就使第三分区的部分缺陷单元相互接触。

表3 试件内部损伤和破坏单元分布(截面Ⅰ)

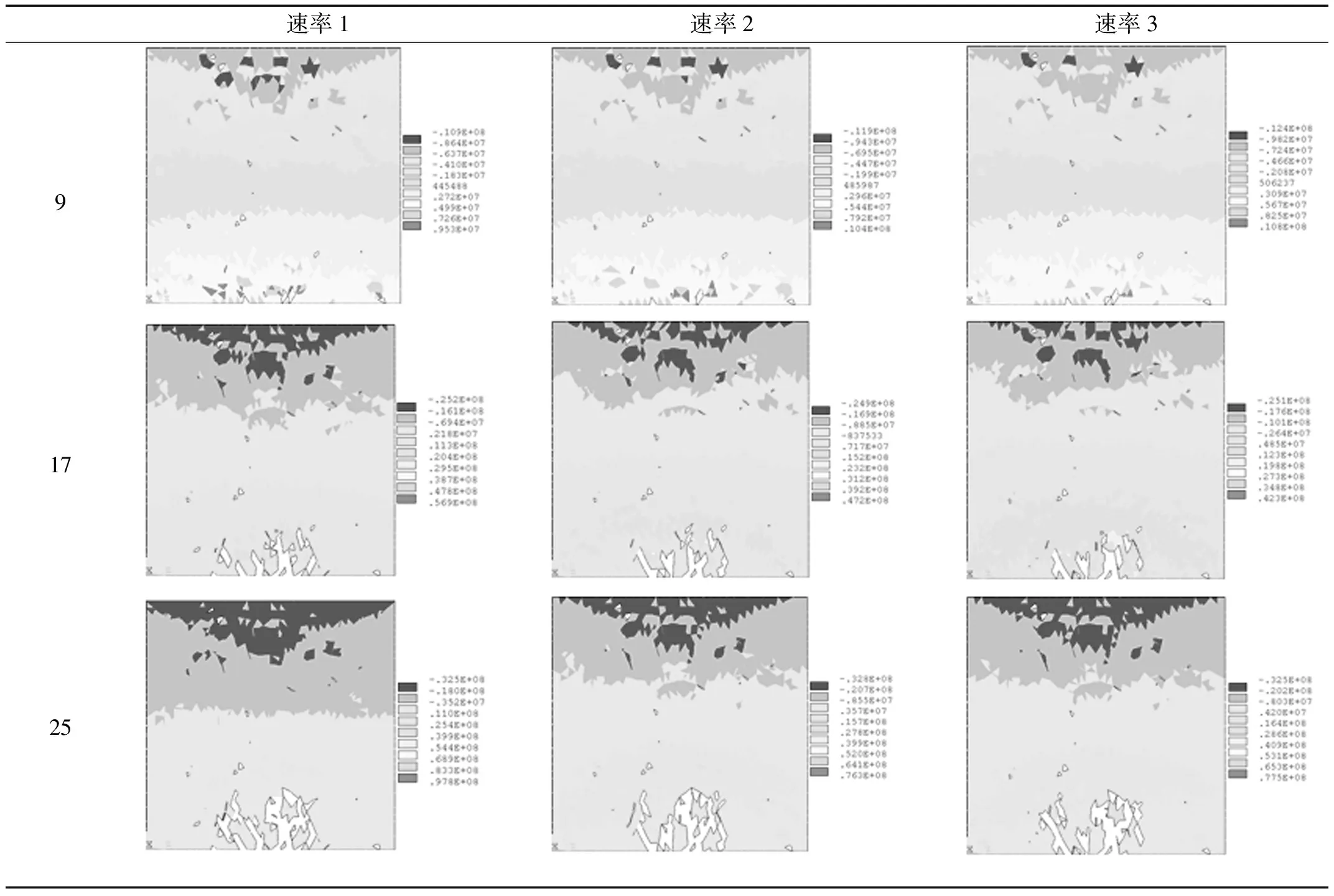
表4 混凝土缺陷试件内部水平向应力分布(截面Ⅰ)

加载中期，在拉应力作用下，第三分区出现了较多数量的细观微裂纹，裂纹的出现缓解了缺陷单元周围的应力集中现象，冲击荷载速率越高，细观微裂纹数量越多，应力释放越充分，缺陷单元周围的应力集中现象越不明显。相当数量的细观微裂纹向第二分区发展，除了在微裂纹顶端附近出现应力集中现象之外，在微裂纹途径缺陷单元时，也会在二者之间出现新的应力集中区域，使缺陷单元与微裂纹相互接触，接触后的微裂纹往往会改变方向继续发展。虽然缺陷单元能够改变微裂纹的发展方向，但是它不能使微裂纹向试件中部发展的总体趋势发生改变。

加载末期，宏观裂纹数量增加，应力释放更充分，拉应力作用范围正在从第三分区逐渐向第二分区移动，这也代表着宏观裂纹的运动方向。宏观裂纹移动过程中，大部分的应力集中现象出现在其顶端附近或者缺陷单元和宏观裂纹之间，内部缺陷在此时对应力分布的影响力较弱。

2.3 混凝土缺陷模型应变分布

混凝土缺陷模型在加载过程中水平向应变分布如表5，缺陷单元对试件应变分布的影响主要通过微裂纹的形态和分布位置体现。加载初期，微裂纹数量较少，缺陷单元对应变分布影响较小。加载中期，由于水平向应变分布受微裂纹形态和分布位置影响较显著，所以当冲击荷载速率不同时，缺陷单元对水平向应变的影响与加载速率成正比。加载末期，虽然冲击荷载速率不同，但是此时宏观裂纹大量增长，水平向应变受内部缺陷的影响明显减小，可以忽略。

表5 混凝土缺陷试件内部水平向应变分布(截面Ⅰ)

3 定量化分析

在之前分析的基础上，对三个分区中出现变化(指弹性模量、泊松比发生变化的缺陷单元)的缺陷单元的数量进行统计，并称这些缺陷单元为变异缺陷单元，得到图5所示变异缺陷单元数量随荷载步变化曲线。

从图中看出，各个分区中变异缺陷单元数量与冲击荷载速率成正比，第三分区出现变异缺陷单元的时间最早，数量最多，且总数量始终高于其他两个分区，这一规律贯穿整个加载过程。在第17荷载步之前各分区变异缺陷单元数量变化呈缓慢递增趋势，但是当达到并超过第17荷载步时，出现变异数量突增的现象。分区位置越靠近试件底部，突增现象越明显，例如：在速率1下，第17荷载步时，对应的三个分区的变异缺陷单元数量由之前的第一分区78个，第二分区228个，第三分区334个，增长到第一分区92个，第二分区261个，第三分区387个，伴随着试件内部大量裂纹的产生，变异缺陷单元数量出现突增现象；加载末期，不同冲击速率使试件内部缺陷单元发生变异的数量仍与加载速率成正比，速率1、速率2和速率3在第25荷载步，第三分区的变异缺陷单元总数分别为：611、586、549个。同时可以观察到，试件接近失稳时，变异缺陷单元数量基本保持不变，这主要是因为试件内部出现大量宏观裂纹使应力释放较充分，拉应力集中区域面积减小。

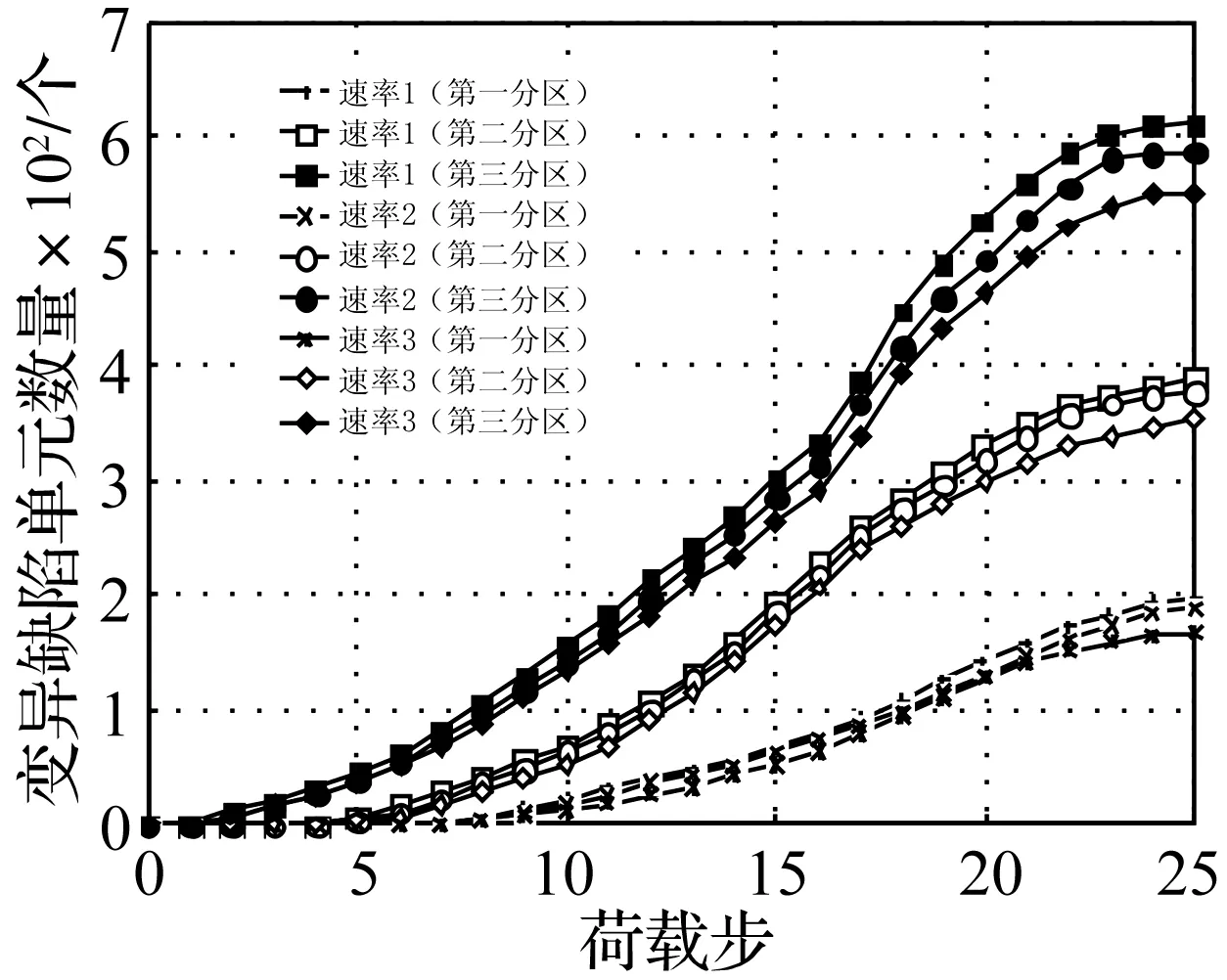
图5 荷载步-变异单元数量分区统计曲线

4 结 论

本文的主要结论有：

(1) 通过本文的方法可以生成混凝土材料中的天然缺陷，在对模型进行数值试验后发现，在冲击荷载作用下，内部缺陷单元会发生变异，这主要是因为试件内部的应力集中、拉应力作用、以及能量释放所引起的。

(2) 变异缺陷单元数量与冲击荷载速率成正比，且距离试件底部越近的分区，相同荷载步内产生的变异缺陷单元数量越多。

(3) 不同速率冲击荷载作用时，试件内部细观微裂纹在加载初期受缺陷单元影响较大，而随着荷载的增加，试件的破坏，缺陷单元的影响力逐渐降低。从宏观上来看，冲击速率的不同会使宏观裂纹的分布和形态产生影响，但是裂纹朝向试件中部运动的整体趋势不会发生变化。

[1]Cheng C C, Cheng T M, Chiang C H. Defect detection of concrete structures using both infrared thermography and elastic waves [J]. Automation in Construction. 2008, 18(1): 87-92.

[2]丁卫华，陈厚群，尹小涛，等. 类岩石材料 CT 动载试验装置的关键技术研究[J]. 岩石力学与工程学报, 2009, 28(8)：1620-1628.

DING Wei-hua, CHEN Hou-qun, YIN Xiao-tao, et al. Study of key techniques of dynamic loading ct test device for rock-like material [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(8): 1620-1628.

[3]丁卫华，陈厚群，党发宁，等. 与医用CT配套的便携式材料试验机的研制及其在混凝土损伤研究中的应用[J]. 实验力学，2009，24(3): 207-214.

DING Wei-hua, CHEN Hou-qun, DANG Fa-ning, et al. Manufacture of portable material test device forming a complete set with medical X-Ray CT and its application in concrete damage study[J]. Journal of Experimental Mechanics,2009, 24(3): 207-214.

[4]郑丹，李庆斌.考虑细观缺陷和静力本构的混凝土动力本构模型[J]. 清华大学学报(自然科学版)，2004，44(3)：410-412.

ZHENG Dan, LI Qing-bin, Dynamic constitutive equations forconcrete based on meso-cracks and a static constitutive model [J]. Journal of Tsinghua University(Science and Technology), 2004, 44(3): 410-412.

[5]WU Zhi-min, YANG Shu-tong, HU Xiao-zhi, et al. An analytical model to predict the effective fracture toughness of concrete for three-point bending notched beams[J]. Engineering Fracture Mechanics,2006, 73(15): 2166-2191.

[6]覃源，柴军瑞，党发宁. 用改良模型分析缺陷混凝土梁的动强度[J].土木建筑与环境工程，2012，34(4): 85-90.

QIN Yuan, Chai Jun-rui, DANG Fa-ning. Numerical analysis on the modified model to the dynamic strength of defective concrete beam [J]. Journal of Civil, Architectural & Environmental Engineering, 2012, 34(4): 85-90.

[7]覃源，柴军瑞，党发宁. 适用于农田水利建筑物的改良型数字混凝土模型[J].河北农业大学学报，2012，35(2): 130-135.

QIN Yuan, Chai Jun-rui, DANG Fa-ning, The improved random aggregate model of concrete for irrigation and water conservancy [J]. Journal of Agricultural University of Hebei, 2012, 35(2): 130-135.