随机失谐周期压电Timoshenko 梁的波动局部化研究

丁 兰，尹 涛，朱宏平

(1.华中科技大学 土木工程与力学学院，武汉 430074;2.武汉大学 土木建筑工程学院，武汉 430072)

智能材料和结构在使用过程中能够感知外界环境的变化，并能针对这种变化做出适当的反应。因其具有自感应和主动控制的能力，所以被广泛应用于各种工程领域。在各种智能材料中，压电材料在今后的智能结构振动控制研究和工程应用中占有极其重要的地位，特别是压电周期结构得到了越来越广泛的应用［1］。周期结构具有通频和禁频等特殊的力学性质，而失谐周期结构还会表现出振动及波的局部化特性［2］。局部化导致波动幅值沿失谐周期结构以空间指数形式衰减，利用此性质即可有效控制结构振动在特定频率范围内的传播。

由于力电耦合效应的影响，压电周期结构将呈现一些新的物理性质，对其进行的研究也会变得复杂。以往的研究多局限在纯弹性周期结构方面，近年来一些学者开始着手研究周期压电结构中的振动波传播及局部化问题。Baz等［2］对周期压电质量－弹簧系统的振动主动控制进行了研究;Li等［3］研究了层状周期压电复合材料结构中的波动局部化问题，并利用Lyapunov指数方法给出了结构中局部化因子的表达式。Wang等［4］研究了Rayleigh表面波在随机失谐压电声子晶体中的传播，得出了一些有意义的结论。上述研究对象都是针对周期性地嵌有压电材料的结构，而就目前的研究现状来看，对其它类型的周期压电智能结构的相关研究，仅有为数不多的报道，如 Thorp等［1，5］分别针对周期压电贴片杆结构中的振动波传播与局部化以及板结构的振动主动控制等问题进行了研究。显然，对此种表面粘贴压电片的周期结构的波传播及其局部化问题的研究尚不够深入，有待更进一步地开展。自从Lin等［6］首次利用传递矩阵方法研究了波在加固板结构中的传播特性，大部分学者直接求解结构的运动方程得到传递矩阵，对于大型复杂结构运动方程的求解相对困难，而 Solaroli等［7－8］则采用有限单元方法得到周期加固壳和叠合梁结构的传递矩阵，为本文分析周期性地粘贴压电片的Timoshenko梁结构提供了参考。

本文基于Timoshenko梁理论，考虑基梁和压电片的转动惯量和剪切效应，研究了轴－弯耦合随机失谐压电Timoshenko梁中的波动局部化问题。采用有限单元法和传递矩阵法相结合，提取了结构的动刚度矩阵，推导了结构相邻胞元间的传递矩阵，并给出了局部化因子的表达式，进而分析了几何尺寸和材料特性失谐对周期压电结构波动局部化的影响，对失谐压电周期结构振动控制研究提供了理论参考。

1 轴－弯耦合压电Timoshenko梁的传递矩阵

图1所示为一周期性粘贴压电片的弹性梁。设压电周期结构中含有n个胞元，每个胞元中含有两个子结构，分别称为子结构1和子结构2。为使问题简化，假设压电层和基梁完好联结无滑移，且具有相同的横向位移w1(x，t)和转角ψ1(x，t)，其中下标1代表子结构1。

图1 周期压电梁的结构简图Fig.1 Schematic diagram of the periodic piezoelectric beam

将每层均作为Timoshenko梁考虑，弹性－压电双层梁(子结构1)的变形见图2。

图2 弹性－压电双层梁的变形示意图Fig.2 Deformation of the elastic-piezoelectric two-layer beam

对于界面层完好联结的情况，

式中，u1b、up、Hb和Hp分别为基梁和压电层的轴向位移和厚度;下标b和p分别表示基梁层和压电层。

压电材料在轴向荷载作用下的本构方程为［9］

式中，σ和ε分别为x方向的应力和应变;D和U分别为电位移和电场强度;CD11、βS33和h31分别为弹性刚度、介电常数和压电常数。

在闭路状态下，运用方程(2)中的本构关系，子结构1的势能V1和动能T1可表示为

其中，E、G、A、I、κ 和 ρ分别为压电层和基梁的杨氏模量、剪切模量、横截面面积、惯性矩、横截面抗剪形状系数和密度。

子结构2的势能V2和动能T2可分别表达为

其中，u2b、ψ2和w2分别为子结构2的轴向位移、转角和横向位移。

将各子结构的运动表示为位移自由度和形函数的级数:

式中，i代表子结构编号。形函数 Niu(x)、Niw(x)、Niψ(x)分别表示为［10］

式中

节点自由度向量为

其中，下标L和R分别代表子结构1和子结构2的左右节点。

将式(7)代入式(3)和(4)，并利用式(1)消除up，可得子结构1的势能和动能

同理，将式(7)代入式(5)和(6)可得子结构2的势能和动能

式中，［K1］、［K2］、［M1］和［M2］分别为子结构 1 和子结构2的刚度矩阵和质量矩阵:

当周期结构以频率ω振动时，利用上式(17)－(20)可得子结构1和子结构2的动刚度矩阵

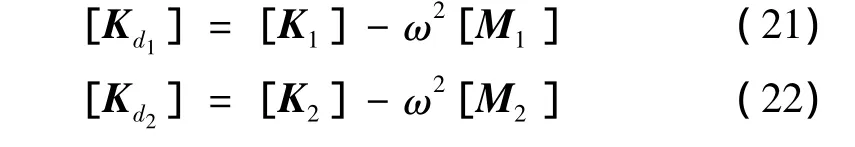
根据动刚度矩阵，第j个胞元中各个子结构的动态运动方程可表示为

经调整，式(23)和(24)可表达为

两个子结构界面处满足

式(27)可以表示为如下矩阵形式

其中，

I为3阶单位矩阵。

利用式(25)和(28)，得到第j个胞元左右两端状态向量间的关系式为

式中T'=T'2J－1T'1为第j个胞元中的传递矩阵。

第(j－1)个胞元右端和第j个胞元左端界面处满足

代入(30)得第(j－1)个胞元和第j个胞元状态向量间的关系式为

由上式可见，T(j)=T'J－1=T'2J－1T'1J－1即为两相邻胞元间的传递矩阵。

2 波动局部化

Lyapunov指数是对相空间中相邻相轨线的平均指数发散程度或收敛程度的度量，它定性地和定量地对动力系统的力学行为进行了有力的描述［11］。研究周期结构中弹性波的传播和局部化时，引用Lyapunov指数的概念，可以提供一种关于弹性波幅值衰减程度的度量指标。局部化导致波动幅值沿失谐周期结构渐近地以空间指数形式衰减，而相应的波动幅值的空间指数衰减常数称为局部化因子。因此，局部化因子用来表示弹性波沿周期结构传播时，波动幅值的空间指数衰减程度［11］。

根据周期结构的对称性，可以证明，Lyapunov指数总是以互为相反数的关系成对出现。若结构传递矩阵的阶数2d×2d，(d＞1)，则可将Lyapunov指数按从大到小的顺序排列为

Lyapunov指数中的最小正值λd代表了幅值衰减程度最小的波，它在结构中传播的距离最远，沿结构传输的能量也最远，刻画了系统中弹性波和振动的主要衰减特性。因此，最小正的Lyapunov指数定义为局部化因子［3－4］。

Wolf［12］给出了计算连续型动力系统中 Lyapunov指数的方法，借鉴此方法，可以给出离散型系统中Lyapunov指数的计算方法。对于传递矩阵阶数为2d×2d的结构，为了计算第m(1≤m≤2d)个Lyapunov指数，需选择m个正交的2d阶初始单位状态向量u(0)1，u(0)2，…，u(0)m，利用式(32)可计算出每次迭代的状态向量。对于第j次迭代

根据Wolf算法，第m(1≤m≤2d)个Lyapunov指数的表达式为:

式中n为周期结构的胞元数。

利用式(36)，可以计算出 d对互为相反的 Lyapunov指数，第d个Lyapunov指数λd即为局部化因子。对于本文中的谐和周期结构，相邻胞元间的传递矩阵T(j)保持不变，且其维数为6×6，因此局部化因子为λ3。利用局部化因子即可分析失谐周期结构的波动局部化现象。

3 算例及分析讨论

根据上述理论模型，本文考虑不同结构尺寸和材料参数失谐对结构局部化的影响。其中，基梁弹性材料采用铝和钢两种，压电材料采用 PKI 502［9，13］，子结构的长度l2=5l1=0.5 m，所用到的材料参数如表1所示。计算过程中取无量纲频率作为自变量。

表1 基梁和压电层的材料常数表Tab.1 Material properties of the base beam and piezoelectric layer

3.1 长度l2失谐

基梁弹性材料为铝，考虑子结构2的长度l2失谐，设其服从均值为l'2=0.5 m，变异系数为δ的均匀分布，则 l2的取值范围可表示为［3－4］

引入一服从标准均匀分布的随机变量η∈(0，1)，则l2可表示为

图3给出了长度l2失谐，变异系数δ取不同值时，局部化因子随无量纲频率的变化曲线。

由图3可观察到，当变异系数δ=0时，谐调周期结构存在明显的频率通带和禁带，在无量纲频率区间Ω∈(0，71.5)内，局部化因子 λ3=0，该区间即为频率通带;在频率范围 Ω∈(71.5，145.7)内，局部化因子λ3＞0，该区间即为频率禁带。当变异系数δ＞0时，对应δ=0为频率通带的边界区间，局部化因子也大于零，出现波动局部化现象，表明失谐周期结构在特定频率范围内能控制波在结构中的传播。随着变异系数的增加，禁带的宽度和局部化因子的幅值逐渐增加，该区间的局部化程度相应地增强。因此可以设计不同的变异系数来微调结构的频带区间和局部化程度。

图3 长度失谐下局部化因子随无量纲频率的变化Fig.3 Localization factors versus dimensionless frequencies for disordered length of the purely elastic beam

3.2 压电材料弹性刚度失谐

基梁弹性材料分别为铝和钢，考虑压电材料的弹性刚度失谐，即，此时，弹性刚度均值仍取，分析变异系数不同时压电材料的弹性刚度失谐对周期结构波动局部化的影响，计算结果见图4。

由图4可知，不同的基梁弹性材料对周期压电结构频带特性影响显著，尽管曲线形状类似，但在第一个禁带区间，钢梁的禁带带宽和局部化因子幅值都小于铝梁，表明在此频率范围内，波动在铝梁中的衰减程度更大。因此，可以根据实际需要选择不同的基梁弹性材料，以达到对结构进行有效的振动控制。比较图4中的四个子图可以发现，周期压电结构的局部化行为对压电材料弹性刚度失谐不够敏感，在特定频率范围内，弹性波不仅可以在谐调周期结构中传播，也可在失谐周期结构中传播。这种现象可能是由于压电材料为压电陶瓷材料，其弹性模量和密度等参数都较大，在此周期结构中占弹性刚度较大的组分，因此其变化对结构的局部化影响很小，可以通过调整基梁及压电材料的弹性刚度比以使得振动控制效应显著。

3.3 压电参数对波动局部化的影响

基梁弹性材料为铝，当长度l2失谐且其变异系数δ=0.10，压电材料的压电参数变化，即压电常数h31及介电常数βS33分别选取不同值时，局部化因子随频率的变化曲线如图5所示。

图4 压电材料弹性刚度失谐下局部化因子随无量纲频率的变化Fig.4 Localization factors)versus dimensionless frequenciesfor disordered elastic stiffness of piezoelectric material

图5 压电参数变化下局部化因子随无量纲频率的变化Fig.5 Effects of different piezoelectric parameters on localization factors for disordered length of the purely elastic beam with δ=0.10

由图5可见，对于同一失谐度，压电参数对周期结构频带特性及局部化程度影响甚微，不同压电常数和介电常数的结构在低频区内，局部化因子曲线保持不变;在整个频率范围内，频率通带和禁带带宽几乎相同。但随着压电常数增加，局部化因子的峰值在第一个禁带降低，而在第二个禁带则增加;介电常数的变化规律与其则刚刚相反。

4 结论

本文对随机失谐周期压电Timoshenko梁的波传播及其局部化行为进行了研究。通过数值算例分析得到以下结论:对于本文周期压电梁而言，基梁长度随机失谐仅能轻微地改变结构的波动局部化特性;失谐度越大，波动局部化程度越强。不同基梁材料对结构的频带特性会有较明显影响;而压电材料参数变化，尤其是压电材料弹性刚度随机失谐对频带性质和局部化程度的影响则非常有限。因此，随机失谐并不能显著地改变本文周期压电梁的波动特性。

［1］Thorp O，Ruzzene M，Baz A.Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches［J］.Smart Materials and Structures，2001，10(5):979－989.

［2］Baz A.Active control of periodic structures［J］.ASME，Journal of Vibration and Acoustics，2001，123(4):472－479.

［3］Li F M，Wang Y S.Study on wave localization in disordered periodic layered piezoelectric composite structures ［J］.International Journal of Solids and Structures，2005，42(24－25):6457－ 6474.

［4］Wang Y Z，Li F M，Huang W H，et al.The propagation and localization of Rayleigh waves in disordered piezoelectric phononic crystals［J］.Journal of the Mechanics and Physics of Solids，2008，56(4):1578 －1590.

［5］Spadoni A，Ruzzene M，Cunefare K.Vibration and wave propagation control of plates with periodic arrays of shunted piezoelectric patches［J］.Journal of Intelligent Material Systems and Structures，2009，20(8):979 －990.

［6］Lin Y K，Mcdaniel T J.Dynamics of beam-type periodic structures［J］.Journal of Engineering for Industry，1969，91(4):1133－1141.

［7］Solaroli G，Gu Z，Baz A，et al.Wave propagation in periodic stiffened shells:spectralfinite elementmodeling and experiments［J］.Journal of Vibration Control，2003，9(9):1057－1081.

［8］Yeh J Y，Chen L W.Wave propagations of a periodic sandwich beam by FEM and the transfer matrix method ［J］.Composite Structures，2006，73(1):53 －60.

［9］Lee U，Kim J.Dynamics of elastic piezoelectric two-layer beams using spectral element method ［J］.International Journal of Solids and Structures，2000，37(32):4403－4417.

［10］诸葛荣，陈全公.框架振动的有限元分析－Timoshenko梁理论的应用［J］.上海海运学院学报，1982，3(4):9－24.ZHUGE Rong，CHEN Quan-gong.The finite element analysis for truss vibration-the application of Timoshenko beam theory［J］.Journal of Shanghai Maritime University，1982，3(4):9－24.

［11］陈阿丽，李凤明，汪越胜.失谐压电周期结构中波动的局部化［J］.振动工程学报，2005，18(3):272－275.CHEN A-li， LiFeng-ming， WangYue-sheng. Wave localization in disordered periodic piezoelectric structures［J］.Journal of Vibration Engineering，2005，18(3):272－275.

［12］Wolf A，Swift J B，Swinney H L，et al.Determining Lyapunov exponents from a time series［J］.Physica D，1985，16(3):285－317.

［13］Lee U，Kim J.Spectral element modeling for the beams treated with active constrained layer damping ［J］.International Journal of Solids and Structures，2001，38(32－33):5679－5702.