一种自适应前瞻的微线段速度平滑插补算法
陈铮杰,赵东标,李克强
(南京航空航天大学 机电学院,江苏 南京 210016)
一种自适应前瞻的微线段速度平滑插补算法
陈铮杰,赵东标,李克强
(南京航空航天大学 机电学院,江苏 南京 210016)
为满足微小线段高速加工的需求,基于微小线段转接处速度对转接夹角大小敏感的特性,提出了一种新的微线段转接算法,在线段拐角处插入转接角的角平分线进行转接,提高了转接处速度,转接处满足误差约束和加速度约束。在分析微小线段各转接处速度大小基础上,算法自适应地分割前瞻段数。针对S型曲线加减速计算复杂的弊端,简化其加减速规律,通过正、反向速度规划,求解最大进给速度,实现微线段段内以及段间的速度平滑。
速度转接;S型曲线加减速;自适应前瞻
传统复杂曲线曲面零件的加工方法通常是CAD/CAM软件用直线段逼近原轨迹,生成大量连续微线段,并将加工程序发送给数控系统。传统的直线插补算法单独处理每段微线段并执行速度规划,程序段始末速度均为零,导致机床频繁加减速,使加工效率低,加工质量差,电机寿命短。
很多学者对连续微线段高速转接加工算法进行了研究[1-11]。王宇晗[1]等导出了转接进给速度约束条件,建立直线加减速速度转接模型。李小清[2]等建立了S型曲线加减速速度转接算法模型,并进行了仿真验证。叶佩青[3]等在直线段连接处插入一段线段,适当降低了连接处的部分精度,实现了微线段的连续插补控制,但仅适用于相邻线段夹角较小的情况。张立先[4]等提出了拐角多周期过渡算法,以多段直线逼近原微线段转接处轨迹,提高了加工速度,并在后续的文献[5]中采用S型加减速方式,减少了机床振动,但为了满足插补的实时性要求作了近似计算处理。张得礼[6]等提出采用圆弧过渡法来处理拐角处速度,并给出段间速度平滑计算方法以及段内等效梯形加减速实现S型曲线加减速的实时速度分析方法。文献[7]根据微线段的近似曲率半径自适应调整进给速度,并用S型加减速进行了前瞻速度规划。文献[8]应用离散化S型曲线加减速规律求解最优衔接进给速度,并根据加工段过渡情况自动调节前瞻预读段数。
本文提出了一种微线段高速转接算法,满足转接处误差约束和加速度约束,并采用简化S型曲线加减速规律进行速度前瞻,调整进给速度,使后续加工段满足速度可达性条件并进行平滑过渡。
1 微线段速度转接算法
微线段速度转接模型如图1所示,第i段与(i+1)段路径转接处为Pi,夹角为αi。假设第i段线段终点Pi处存在加速度ai,e,方向同APi,则第(i+1)段线段起点Pi处存在大小相等、方向同PiB的加速度ai+1,s。在Pi处转接瞬间,系统产生加速度方向突变。为避免产生冲击,简化后续的分析计算,设定在线段转接处加速度大小为零。通常的速度转接方法是以夹角α为参变量控制转接速度,使在转接点Pi前后速度大小相等,速度矢量的方向改变。设转接处速度大小为vi,根据三角函数公式得出:
式中:amax为机床最大允许加速度;T为插补周期;αi∈[0,180°]。
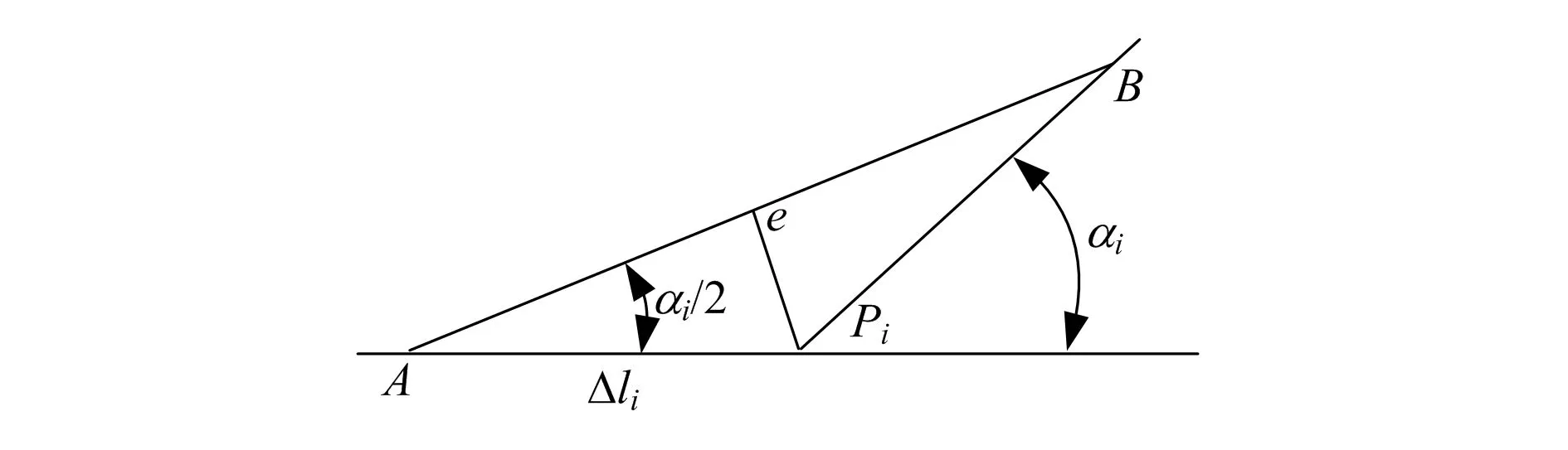
图1 微线段速度转接模型
本算法在第i段和第(i+1)段路径间加入线段AB,A点距原转接点距离为Δli,并使AB和APi的夹角为αi/2,则线段转接点由Pi变为A点和B点,AB段保持匀速运动,转接处速度约束条件变为:
当αi很小时,sinαi/4≈αi/4,最大转接速度提高了约1倍。
根据文献[11],转接处的误差约束条件为:
式中:e为系统允许最大误差。
由最大速度限制,得:
式中:vmax为系统允许最大进给速度。
令系统插补周期T=1ms,最大加速度amax=1 000mm/s2,最大允许误差e=1μm,速度约束曲线如图2所示。
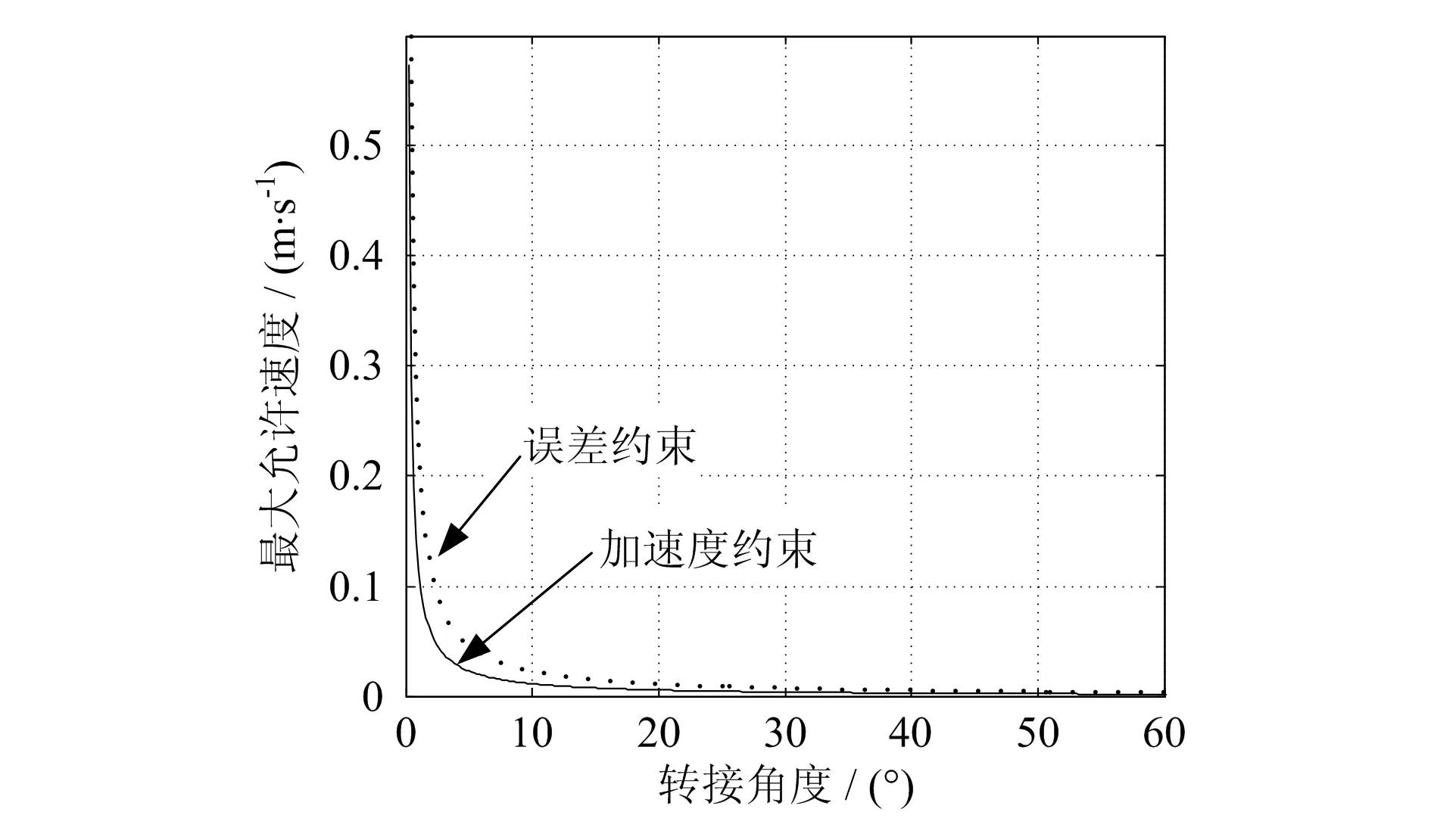
图2 转接速度与转接角关系
如图2可见,加速度约束曲线在误差约束曲线的下方。若减小转接角,能增加转接速度。
2 自适应前瞻速度规划
2.1前瞻段数的自适应选取
如图3所示,加工路径中局部有4个转接处:Pi-2,Pi-1,Pi,Pi+1。线段间夹角分别为:αi-2,αi-1,αi,αi+1。图中,αi大于其余3个夹角,αi>αi-1且αi>αi+1。根据1中速度约束条件,Pi处允许的最大转接速度vi最小,因而在前瞻速度规划中,将Pi作为前瞻段数的分割点。把两个分割点之间的微线段作为整体进行前瞻速度规划。规划完成后,从Pi处开始继续向后寻找分割点,计算前瞻段数,重复上述步骤,直到程序结束。整个加工轨迹起始点和终止点速度为零,中间各分割点的速度为最大允许转接速度。传统的算法前瞻段数固定,段首和段尾的速度为零。要增加转接速度,需增大前瞻段数。而前瞻距离越长,实时性越难保证。本算法与传统算法相比,实现了前瞻段数的自适应选取,减少了加减速的变化,提高了整体插补速度。

图3 局部微线段转接角
2.2前瞻速度规划
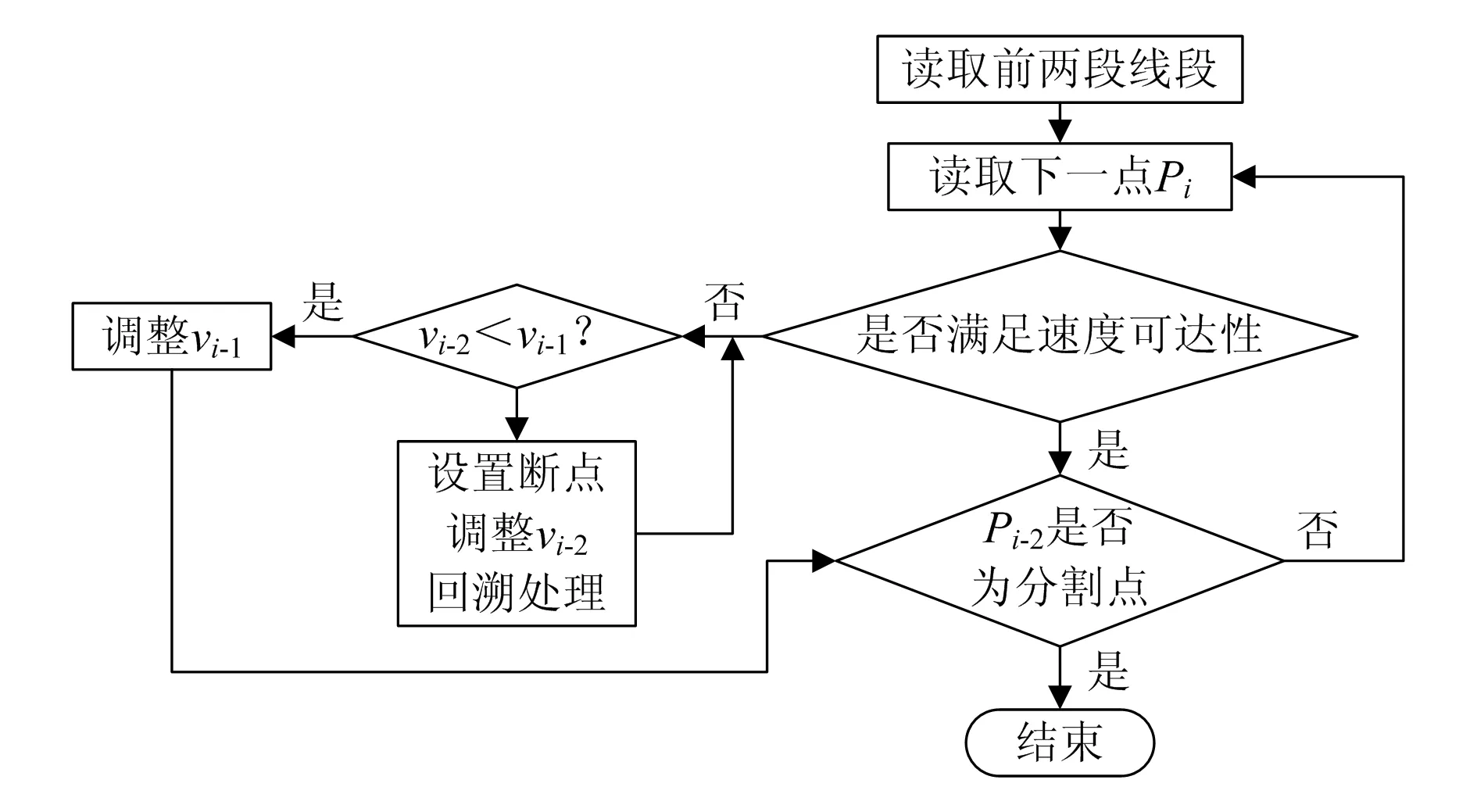
按照2.1节确定的前瞻段数,从第一段线段开始,向后进行速度可达性判断,如果该线段起始速度vs小于终止速度ve,且ve不可达,则需减小ve,使之满足可达性。如果vs大于ve,且速度不可达,则需设置标志点,减小vs并向前进行回溯处理,直到遇到满足速度可达性的线段,然后回到标志点继续进行前瞻处理,直到程序段结束。
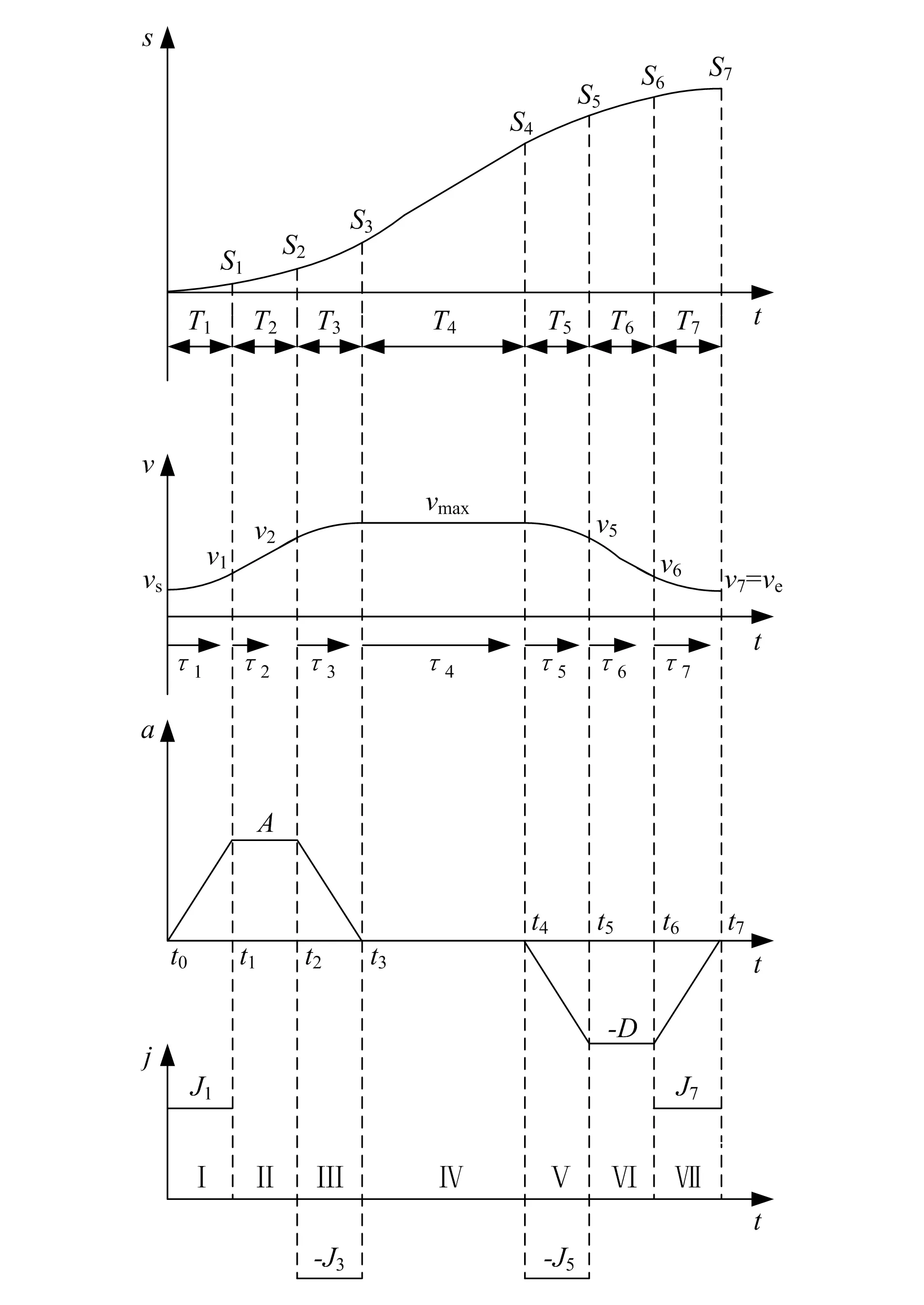
图4 S型曲线加减速示意图
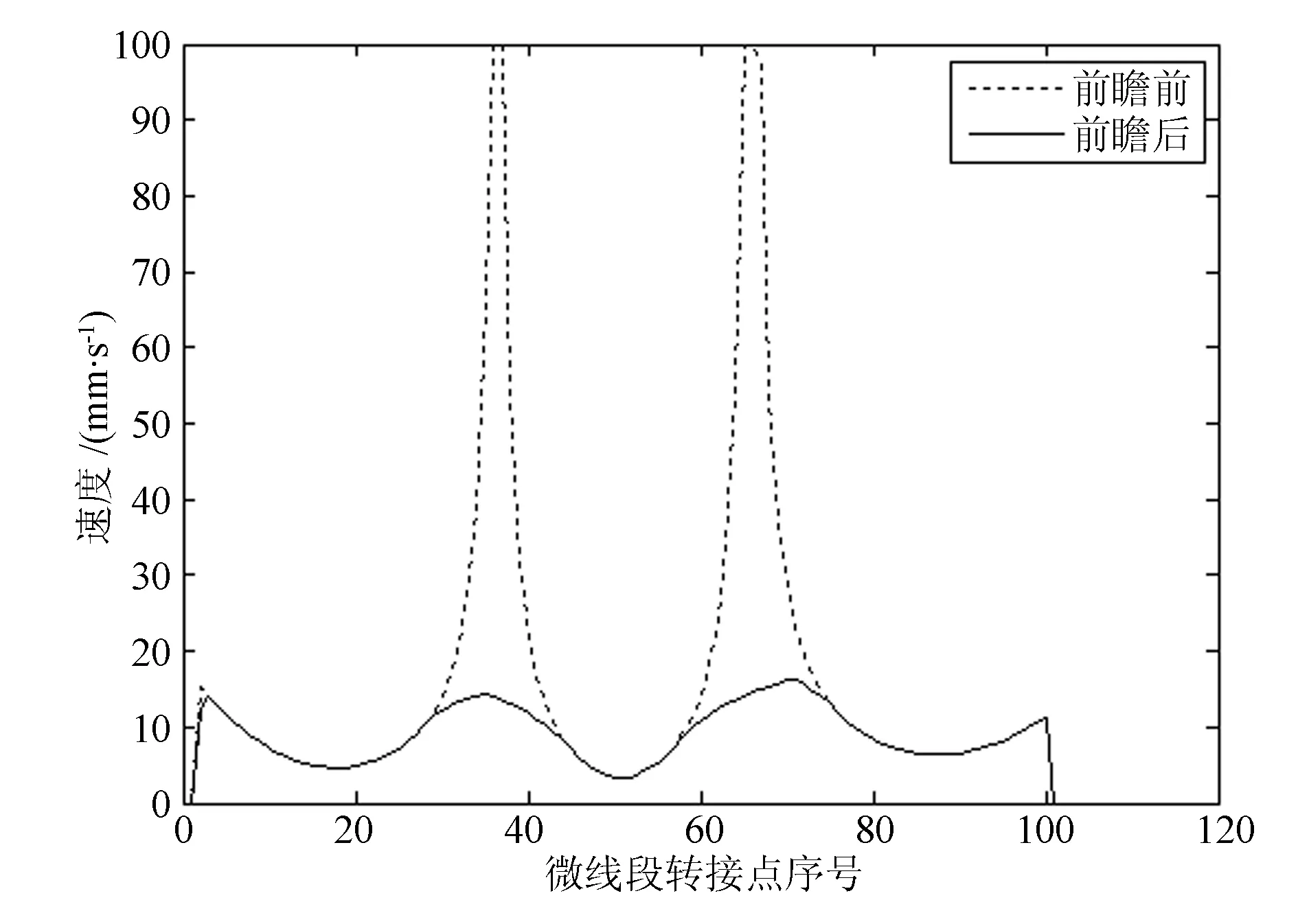
S型曲线加减速过程如图4所示,其中sk(k=1,…,7)表示各阶段累积位移值;vs为起始速度;ve为终止速度;vi(i=1,…,7)为各段过渡时刻的速度;Ti(i=1,…,7)为各阶段运行时间;τk(k=1,…,7)为各阶段作为起始点的时间;tk为各阶段时刻;A,-D为最大加速度;J1,-J3,J5,-J7为最大加加速度;Ⅰ,Ⅱ,…,Ⅶ表示加减速过程各个阶段。为简化计算,本文采用一段线段内只有加速过程或减速过程的方法,最多包含Ⅰ,Ⅱ,Ⅲ或者Ⅳ,Ⅴ,Ⅵ 3个阶段。结合图5所示转接图,速度可达性分析判断第i段线段中,从起始速度vs到终止速度ve所需最短距离Si是否小于该段插补距离li。具体分析如下(假设vs 图5 加工轨迹局部转接图 前瞻控制框图如图6所示,步骤具体如下: 图6 前瞻控制框图 步骤1, 顺序读取第一段两个端点Pi-1,Pi。初始化起始速度为零,计算线段长度。 步骤2, 读下一段线段的终点Pi+1,根据1中速度约束条件计算Pi处最大允许速度vi,并计算αi和Δli。 步骤3, 判断vi-1到vi是否满足速度可达性。 当不满足时,若vi-1 步骤4, 比较各转接角α的大小,找到转接角度最大点,以此作为前瞻段数分割点。判断依据为:若vi-1≤vi-2,且vi-1 原二维NURBS曲线部分如图7所示,用微线段逼近,得微线段长度分布,如图8所示。共获得离散点101个,微线段100条,微线段最大长度为0.420mm,最短长度为0.105mm。 图7 原NURBS曲线轨迹图 图8 微线段长度分布图 取系统最大允许速度vmax=100mm/s,加速度A=D=200mm/s2,加加速度J1=J3=J5=J7=20m/s3,插补周期T=1ms,系统允许误差e=1μm。对微线段整体进行前瞻S型加减速速度规划,如图9所示。 图9 前瞻效果对比图 如图9所示,虚线表示前瞻前各微线段转接点最大允许进给速度。通过自适应前瞻速度规划,求得轨迹中第18,51,87个点为速度分割点。结合简化的S型加减速曲线进行速度可达性分析,有效降低了速度过大点,增加了插补轨迹的速度平滑性。 本文基于微线段插补转接速度对转接夹角敏感的特性,将角平分线插入转接处,提高了转接速度。本前瞻算法根据微线段转接速度,能自适应地划分前瞻段数。采用简化的S型加减速曲线进行前瞻速度规划,使微线段间速度进行平滑过渡,能提高加工工件的表面质量。 [1] 王宇晗, 肖凌剑,曾水生, 等. 小线段高速加工速度衔接速度模型[J]. 上海交通大学学报, 2004, 3(6): 901-904. [2] 李小清, 朱凯. 数控加工小线段高速平滑衔接插补算法[J]. 组合机床与自动化加工技术, 2010(9): 1-5. [3] 叶佩青, 赵慎良. 微小线段的连续插补控制算法研究[J].中国机械工程, 2004, 15(15): 1354-1356. [4] 张立先, 孙瑞勇, 高小山, 等. 数控机床高速微线段插补算法与自适应前瞻处理[J]. 中国科学: 技术科学, 2011, 41(6): 774-789. [5] 张立先, 李洪波, 高小山, 等. 高速CNC加工S型加减速方式连续小直线段插补算法[J]. KLMM, Chinese Academy of Sciences, 2010, 29: 227-237. [6] 张得礼, 周来水. 数控加工运动的平滑处理[J].航空学报, 2006, 27(1): 125-130. [7] Dong J C, Wang T Y, Li B, et al. Smooth federate planning for continuous short line tool path with contour error constraint[J]. International Journal of Machine Tools and Manufacture, 2014, 76: 1-12. [8] 汪霖, 曹建福. 高速装备前瞻自适应速度优化算法[J]. 计算机集成制造系统, 2010, 16(5): 998-1005. [9] Luo F Y, Zhou Y F, Yin J. A universal velocity profile generation approach for high-speed machining of small line segments with look-ahead [J]. International Journal of Advanced Manufacturing Technology, 2007, 35(5): 505-518. [10] 邬义杰, 商允舜. 微小直线段插补终点控制算法研究[J]. 组合机床与自动化加工技术, 2006(2): 1-5. [11] 吕强, 张辉, 杨开明,等. 数控连续加工中提高轨迹段转接速度的方法研究[J]. 制造技术与机床, 2008(7): 79-83. AnAdaptiveLook-aheadInterpolationAlgorithmofMicroLinewithSmoothVelocity CHEN Zhengjie, ZHAO Dongbiao, LI Keqiang (Nanjing University of Aeronautics and Astronautics, Jiangsu Nanjing, 210016, China) In order to meet the requirements for high-speed machining, it proposes a new transfer algorithm of small line segments, which makes the transfer speed sensitive to the angle between two lines. This algorithm inserts the angle bisector in the corner of two lines to improve the transfer speed, satisfies the error and acceleration constraint. It analyzes the transfer speed of small line segments. The algorithm divides the number of line segments adaptively. According to the disadvantage of computation complexity, the algorithm simplifies the acceleration/deceleration control law of S curve. Through forward and backward speed programming, it calculates the maximum feed rate, implements the smooth velocity in a line and between line segments. Speed Transition; S Curve Acceleration/Deceleration; Adaptive Look-ahead 10.3969/j.issn.2095-509X.2014.03.011 2014-02-26 国家自然科学基金资助项目(51175261) 陈铮杰(1988—),男,浙江上虞人,南京航空航天大学硕士研究生,主要研究方向为机电控制及自动化。 TP273 A 2095-509X(2014)03-0041-04



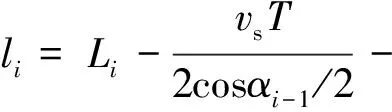


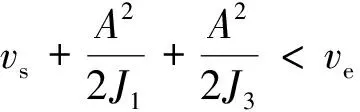
3 仿真验证与分析


4 结束语

